多智能体编队控制中的迁移强化学习算法研究

胡鹏林, 潘泉, 郭亚宁, 赵春晖

(西北工业大学 自动化学院, 陕西 西安 710129)

多智能体系统由多个同构或异构的智能体构成,通过与环境之间的交互,共同完成单个智能体由于能力不够而无法完成的复杂任务。由于多智能体系统的鲁棒性、可靠性、灵活性等独特优势,在航空航天、工业生产、交通运输等领域获得了深入研究和广泛应用[1-3]。编队控制是指智能体在运动过程中,通过建立、保持、变换智能体的空间构型,在克服干扰约束的同时完成特殊的任务规划,保证编队的安全性和高效性。编队控制作为多智能体系统的重要研究内容之一,在军事和民用领域有着广泛应用。

在多智能体编队控制算法的发展过程中,出现了多种控制算法,主要有基于行为的方法、虚拟结构的方法、领航者-跟随者方法、一致性理论等多种控制理论与方法。基于行为法是模仿自然界的动物行为进行编队控制,一般采用鲁棒的分布式控制,具有很强的扩展能力。例如,基于大雁[4]、鸽子[5]、鱼群[6]等生物,提出了大量的编队控制算法。虚拟结构法采用虚拟的刚体结构描述多智能体编队构型,通过相对误差进行控制,具有很高的控制精度。例如,基于虚拟结构法的无人机编队控制[7]、无人船编队控制[8]、多机器人编队控制[9]。领航者-跟随者算法将智能体分为领航者和跟随者,双方之间保持一定距离,保证编队的稳定和安全。基于领航者-跟随者算法研究了无人机编队控制[10]、无人船编队控制[11]、三维空间中编队控制问题[12]。一致性理论是将图论和代数理论结合,通过处理系统误差实现编队控制,例如,基于一致性理论实现无人机的编队和避障控制[13],以及使得非对称移动机器人能够以期望的编队构型移动[14]。

上述多智能体编队控制算法通常需要精确的数学模型来设计控制律,在实际应用中,由于传感器误差、环境干扰等随机因素,通常难以获得精确模型,给多智能体编队控制造成巨大困难。

强化学习(reinforcement learning,RL)不需要太多先验知识和精确的数学模型,成为解决智能体系统控制问题的重要途径[15]。例如,将Q-learning和策略梯度算法结合,提出了多层结构的编队控制算法,使得机器人能够实现设定的编队构型[16]。通过自适应Q-learning算法,实现了障碍环境中编队控制[17]。通过基于RL的多智能体编队控制框架,消除了建模和控制器设计的繁琐工作,解决了复杂环境中编队控制问题[18]。传统的强化学习算法不仅需要大量的样本进行训练,还要求训练和测试数据属于同一个域,随着智能体数量的增加,状态空间呈指数增长,给存储空间和计算能力带来巨大挑战。

迁移强化学习(transfer reinforcement learning,TRL)从简单的源任务中获得知识,求解更复杂的目标任务,并且任务之间相似程度越高,知识的传递就更加容易,从而提高系统的学习效率[19]。按照学习方法可以分为基于样本的迁移、基于模型的迁移、基于特征的迁移,以及基于关系的迁移等多种模式[20]。除了计算机视觉、文本分类、自然语言处理等传统领域外,迁移强化学习逐渐应用在许多新兴的领域。在医学图像领域,由于医学图像的标记通常依赖于有经验的医生,因此,收集足够的训练数据是非常昂贵和困难的,迁移学习技术能很好地帮助医学影像分析[21-22]。在生物信息学领域,生物体之间的组成发生了变化,但其功能可能保持不变,可以借助迁移学习算法来进行生物序列的分析[23-24]。在交通运输领域,迁移学习可以帮助电子监控系统进行交通场景图像的理解,以及驾驶员行为的建模[25-26]。在个性化推荐系统领域,往往训练数据是稀疏的,迁移学习算法可以利用来自其他推荐系统的数据来帮助构建目标推荐系统[27-28]。

本文基于迁移强化学习算法,研究了复杂障碍环境下多智能体编队控制问题。在训练过程中,利用值函数近似算法,解决了任务规模不断扩大带来的存储和计算问题。采用高斯混合模型(Gaussian mixture model,GMM)对源任务进行聚类分析,避免出现负迁移现象,提高了迁移强化学习效率。文章内容安排如下:第1节介绍智能体模型和求解问题的数学描述,第2节介绍基于迁移强化学习的多智能体编队控制算法,第3节通过仿真实验验证了算法的有效性,第4节给出全文总结与未来研究方向。

1 问题描述

多智能体编队控制系统由N个智能体组成,智能体通过复杂的障碍物环境,保持一定的队形到达目标点,同时保证智能体不发生碰撞。智能体i的模型为

xi(t+1)=xi(t)+vcos(Δφi(t))

yi(t+1)=yi(t)+vsin(Δφi(t))

(1)

式中:i∈N={1,2,…,N},v代表智能体的移动速度;φi(t)∈[0,2π]表示t时刻智能体i的航向角,即智能体i的移动方向与x坐标轴正方向的夹角,为了避免出现较大的转弯动作,航向角增量Δφi(t)满足

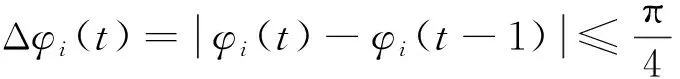
(2)

用si(t)=[xi(t),yi(t)]表示t时刻智能体i的坐标位置,障碍物集合为No={1,2,…,l}。

在多智能体编队中,最优性能指标不是单个智能体的策略达到最优,而是整个编队的策略达到最优,即编队中智能体之间构成合作博弈关系,因此,将多智能体控制任务描述为马尔科夫博弈过程

Γ={S,A,π,R,V}

(3)

(4)

式中,γ表示折扣因子。

由于在学习过程中,奖励函数的作用非常重要,定义智能体i∈N的奖励函数Ri为

(5)

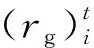
(6)

(7)

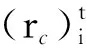
(8)

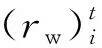
(9)

式中,ww为常系数。在多智能体编队中,智能体i和其他智能体之间进行交互,因此,智能体i的性能指标由自身和其他智能体共同决定,用π-i表述其他智能体的策略,在考虑其他智能体的策略时,智能体i的性能指标为

(10)

则最优价值函数为

(11)

多智能体博弈的策略取决于环境中智能体的联合行为,在其他智能体策略保持不变的情况下,智能体i在状态si的策略

(12)

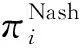
(13)

则(12)式为智能体i的Nash均衡策略,基于Nash均衡策略的价值函数为

(14)

在多智能体编队过程中,采用价值函数

(15)

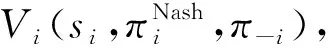
(16)

综上,多智能体编队控制问题可以描述为

(17)

2 基于迁移学习的多智能体编队控制

通过前文获得了多智能体编队控制问题的数学描述以及优化目标。为了应对复杂的多智能体编队环境,提升强化学习速度以及泛化能力,本文引入迁移强化学习算法。如图1所示,迁移强化学习涉及到源任务和目标任务。

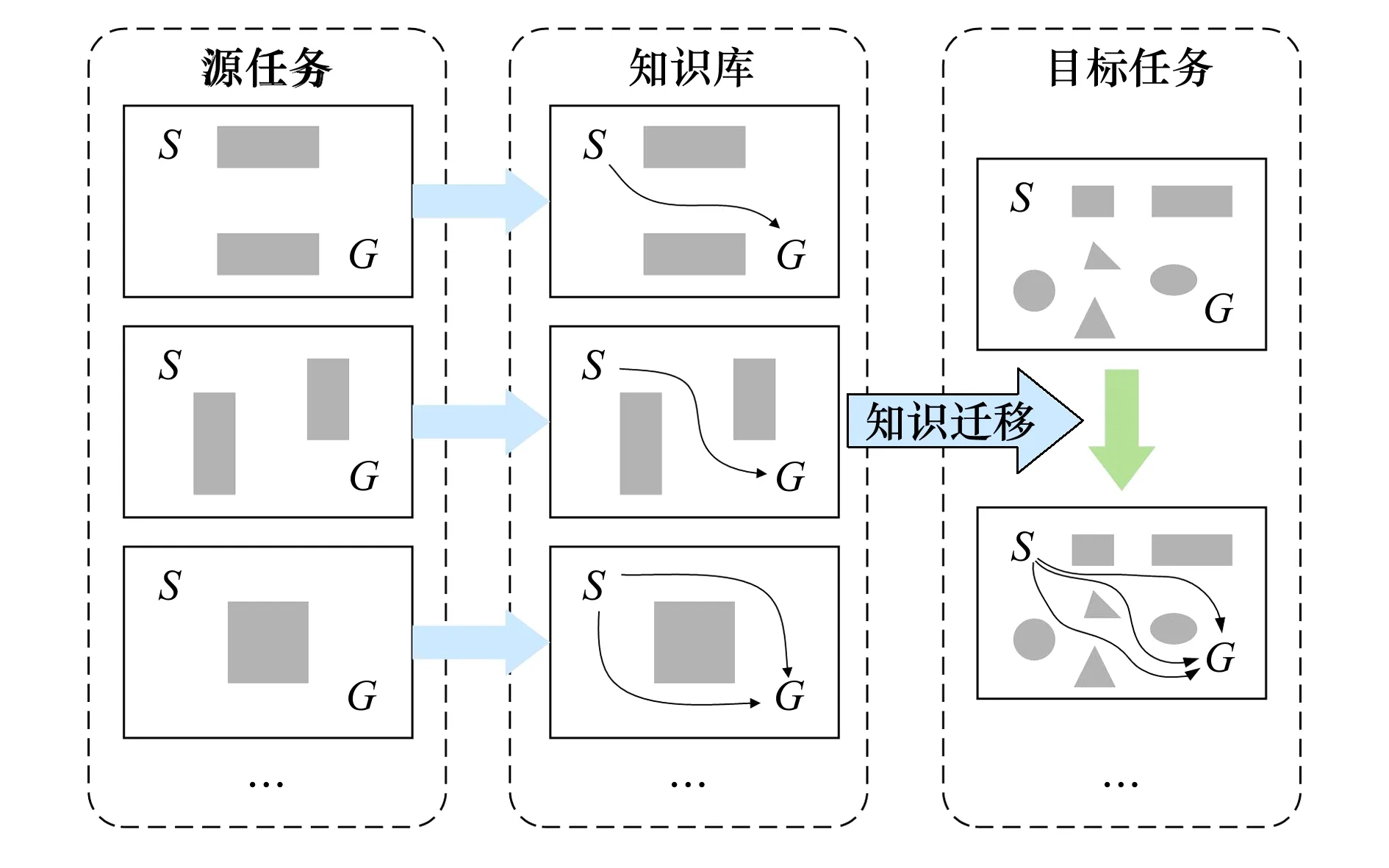
图1 迁移强化学习示意图

基于马尔科夫博弈的描述,多智能体编队控制可以分解为源任务Ms={Ns,Ss,As,Rs}和目标任务Mt={Nt,St,At,Rt}2个子任务。迁移强化学习过程包括2个阶段,首先是知识迁移阶段At,根据目标任务Ug和源任务Us之间的相关性生成合适的知识迁移模型Ut

At:Us×Ug→Ut

(18)

其次是学习阶段Al,结合迁移模型Ut和目标任务Ug,实现目标任务的学习

Al:Ut×Ug→Ug

(19)

下面从源任务和目标任务学习两方面进行论述。

2.1 基于值函数近似的源任务学习

在源任务学习中,为了突出迁移强化学习对训练速度的提升作用,采用Q-Learning算法进行源任务训练,基于值函数近似方法,避免Q表格带来的大规模存储问题。根据(15)式智能体i的值函数为

(20)

值函数可以用线性函数表述为

(21)

式中:φi(si(t))=[φi1(s),…,φim(s)]∈Rm×1是由智能体i的状态构成的m维特征向量;T表示矩阵的转置,用wi=[wi1,…,wim]∈Rm×1表示联合权重向量,使用含有参数wi的值函数表示其真值为

(22)

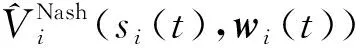
(23)

求参数wi使得(23)式最小,根据最小二乘算法有

(24)

式中

对权重系数的收敛性进行分析,根据(21)和(24)式有

(25)

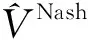
(26)

设ρ,ψ,C均为正数,φt为持续激励信号,满足

(27)

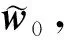
(28)

证明根据(25)式有

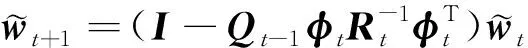
(29)

选择函数Lt

(30)

将(26)式代入(30)式有

(31)

因此得到

(32)

λmin(G-1)ΦΦT≤ΦG-1ΦT

(33)

根据正定矩阵性质有

(34)

根据(26)式有

(35)

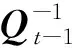
(36)

结合(30)、(32)、(33)、(36)式有

(37)

化简后有

(38)

综上,得到

(39)

取(28)式中的ξ为

(40)

则(28)式成立,wi呈指数收敛,证明完毕。

根据Bellman最优性原理,对价值函数进行更新,智能体i的最优值函数为

(41)

最优动作选择策略为

(42)

完成基于值函数近似的源任务训练。

2.2 基于聚类的目标任务迁移学习

在获得源任务之后,将所有源任务的知识迁移到同一个智能体时,由于任务之间的差异化会导致负迁移。因此将大量训练好的源任务数据进行归类处理,选择与目标任务差异最小的源任务,可以有效避免负迁移现象。本文选用GMM算法对源任务状态进行聚类分析,假设在本文中策略的相似性可以通过相应的值函数来反映,即在相同的奖励函数下,价值函数相似的策略,智能体的运动轨迹是平行或者重合的。

(43)

式中,πi(a|sj)表示在源任务状态sj执行动作a的概率,通过(44)式将值函数映射到集合yi

(44)

设n′为源任务中的分类数量,在获得源任务样本Y=(y1,y2,…,yn′)之后,执行GMM算法

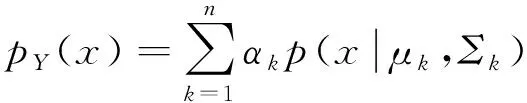
(45)

式中:n为目标任务中智能体数量;αk为高斯混合系数;(μk,Σk)为高斯分布的期望和方差。通过最大似然函数(46)式估计(45)式的参数

(46)

(46)式的对数似然函数为

(47)

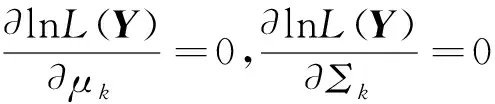
(48)

式中,ζjk表示样本yj中元素的后验概率密度

(49)

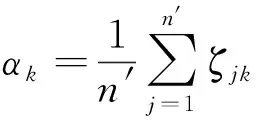
(50)

通过聚类可以得到n′个高斯分布,将源任务状态划分为多个集合,每个集合中的策略是相似的,避免多个具有竞争关系的策略传递给同一个目标任务而引起负迁移现象。

迁移学习的关键是源任务与目标任务之间的相似性,2个任务相似程度越高,迁移学习效果越好。在获得n′个具有高斯分布的源任务集合后,通过康托洛维奇距离度量聚类任务和目标任务之间的相似程度。计算聚类任务Ms和目标任务Mg两者之间的康托洛维奇距离D(Ss,Sg)为

式中:|Ss|,|Sg|表示状态空间的大小;ηij表示si和sj之间距离d(si,sj)的权重值为

(52)

式中,r(si,ai),r(sj,aj)表示奖励值,c∈(0,1)。

根据任务之间的距离度量,选择与目标任务距离最近的源任务类,假设其中有m个源任务,对目标任务Mg中智能体i的值函数进行初始化

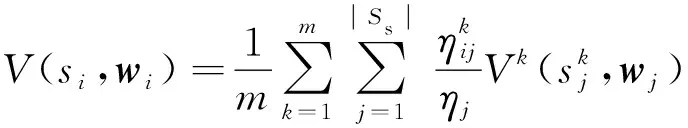
(53)

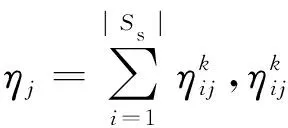
因此,得到基于迁移强化学习的多智能体编队控制算法流程如下:

1) 初始化目标任务Mt,源任务Ms,状态基函数φ(s),权重向量w=1,迭代次数T,最大搜索步数M,折扣因子γ,收敛因子ε。

2) 源任务学习:

3) Fork=1∶Tdo

4) 根据(42)式选择动作a

5) Forl=1∶Mdo

6) 执行a,得到下一状态s′和奖励r

7) 在状态s′执行(42)式

8) 更新状态和动作s←s′,a←a′

9) 根据(24)式更新ws

10) 如果s=sg,‖wt+1-wt‖2<ε进行下一次迭代

11) End for

12) 目标任务学习:

13) 根据(45)式对源任务状态进行GMM聚类分析

14) 根据(51)式选择m个较优的源任务状态

15) 根据(53)式初始化目标任务中智能体的值函数

16) 执行2)～10)进行训练任务,得到策略π*

3 仿真验证与分析

3.1 迁移强化学习过程仿真

本节验证在二维状态空间中迁移强化学习的有效性。智能体最大速度v=0.3 m/s在35 m×35 m的矩形区域运动,用半径为1 m的圆表示智能体和障碍物。根据(5)式设计奖励函数,具体参数设置为:ds=do=dg=1 m,r1=-50,r2=-10,r3=-10,r4=-5,

wg=10,ww=25。学习参数设置为:γ=0.95,T=500,M=5 000,ε=0.1。选择多项式形式的状态基函数如(54)式所示。

对应系数为wi(t)=[wi1,wi2,…,wi27]。

源任务中智能体的起始点为[5,5],[5,25],[25,5],对应的目标点为[30,30],[15,20],[30,15],障碍物为[10,20],[15,15],[20,5],[20,28],[25,20],[30,10]。智能体路径轨迹如图2a)所示,方形代表起始点,五星代表终点。所有智能体能够在复杂环境中,无碰撞地从起始点移动到对应的目标点位置,得到较优的源任务学习样本。

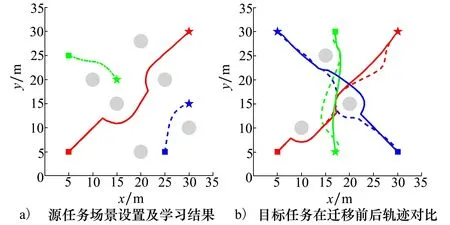
图2 迁移学习效果对比

目标任务中智能体的起始点为[5,5],[17,30],[30,5],对应的目标点为[30,30],[17,5],[5,30],障碍物为[10,10],[15,25],[20,15]。迁移学习前后智能体运动轨迹如图2b)所示,虚线和实线分别表示智能体迁移学习之前和之后的路径轨迹,可以看出后者的路径轨迹明显优于前者,且安全到达各自设定的目标点。为了验证迁移学习效果,在不同的目标环境中,进行了50次重复实验,然后求取平均值,对迁移前后所有智能体到达目标点的总路径、总时长以及成功率进行对比分析,成功率以在规定时间内是否到达目标来判定,通过图3可以看出,迁移学习之后的路径长度明显小于迁移之前的长度,并且用时较少,成功率也有所提高。

图3 迁移强化学习前后的结果对比柱状图

图4展示了任务之间的相似性对于迭代次数及奖励值的影响,横坐标表示源任务和目标任务间的距离,散点表示每次实验的结果,并进行了曲线拟合。可以看出迭代次数随着任务之间距离的增加而增加,并且随着距离的增加,智能体获得的平均奖励值变小。由此可以得出任务之间的相似性越高,迁移效果越好,同时也说明采用GMM算法选择与目标任务差异最小的源任务进行迁移能够有效避免负迁移问题。

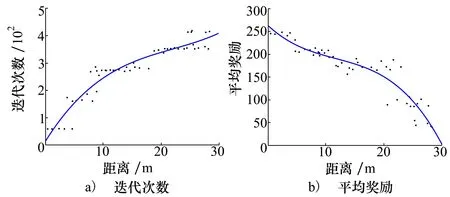
图4 任务相似性对迁移学习结果的影响

在目标任务的基础上,设置障碍物为[10,10],[10,18],[15,25],[17,20],[25,10],验证迁移强化学习算法的避障防撞性能,设置ds=0.5 m。智能体避障与防撞过程如图5所示,每个智能体都到达了指定的目标点位置。图5b)展示了智能体之间的规避过程。避障过程中智能体之间的距离如图6所示,均满足设定的安全距离,没有发生碰撞,保证了智能体的安全运动。关于迭代次数和权重系数w的收敛性在文献[29]中有详细的实验分析。

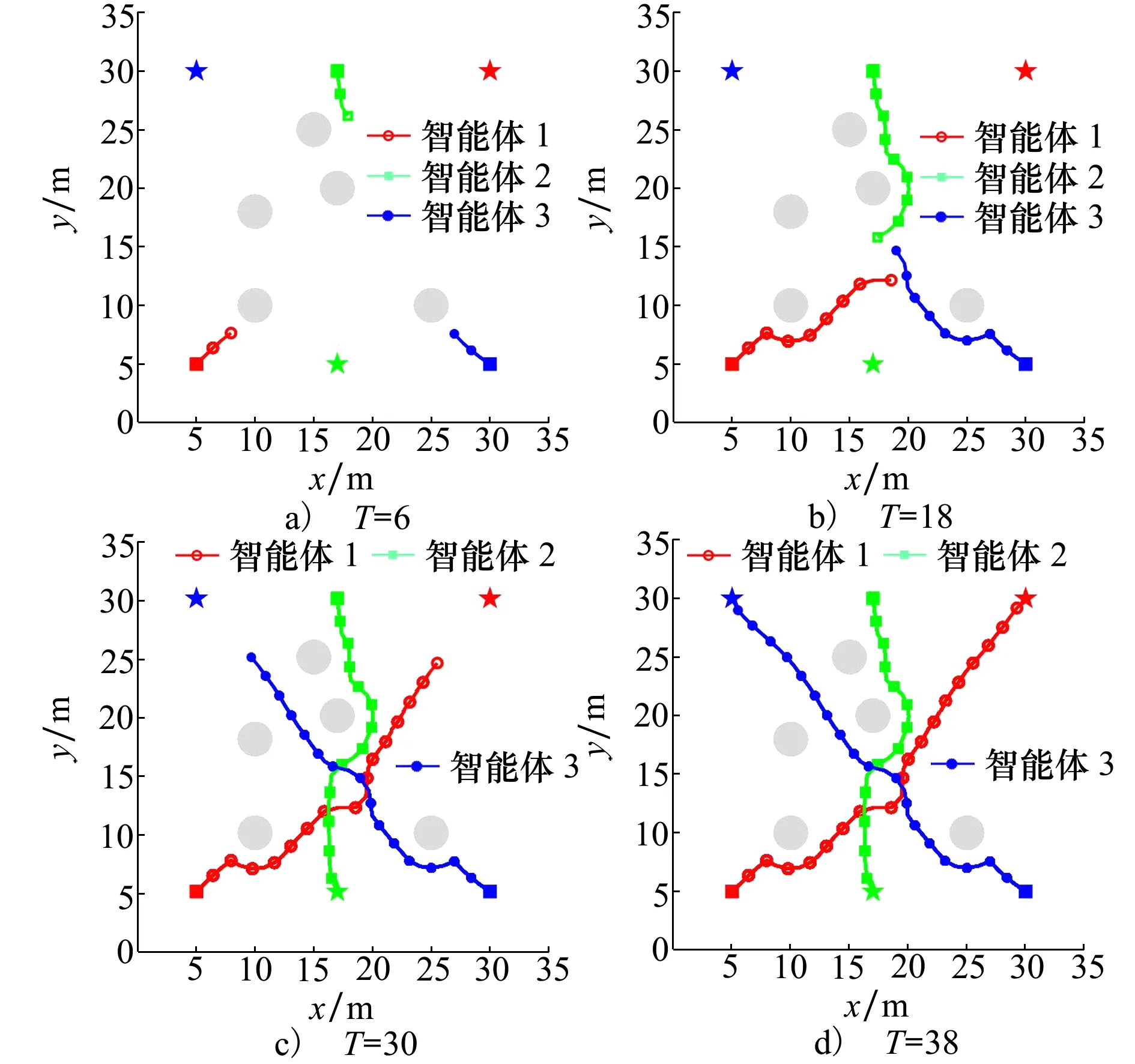
图5 多智能体避障与防撞过程(T表示步数)

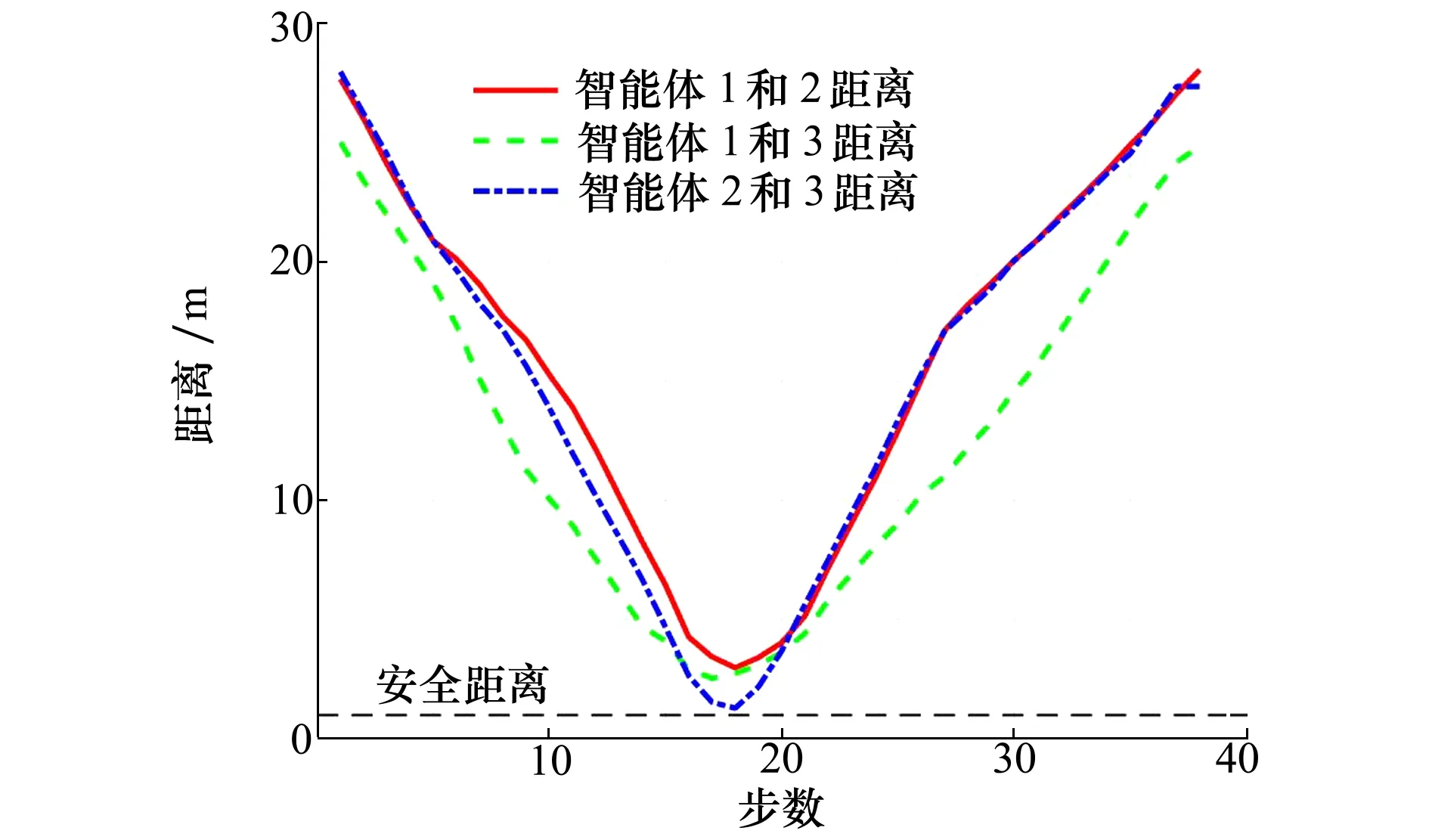
图6 智能体避障过程相互之间的距离

3.2 多智能体编队任务仿真

用4个智能体进行编队控制仿真,编队任务中智能体的起始点为[4.5,26],[5,10],[12,3],[30,5],设置对应的目标点为[28,30],[30,27.5],[32,30],[30,32.5],障碍物为[11,15],[15,23.5],[16,9],[25,10.5],[26.5,23.5]。每个智能体在训练过程中找到各自合适的目标位置,形成对角线长度分别是4 m和5 m的菱形编队,然后保持编队形式运动到目标位置,智能体运动轨迹如图7所示。

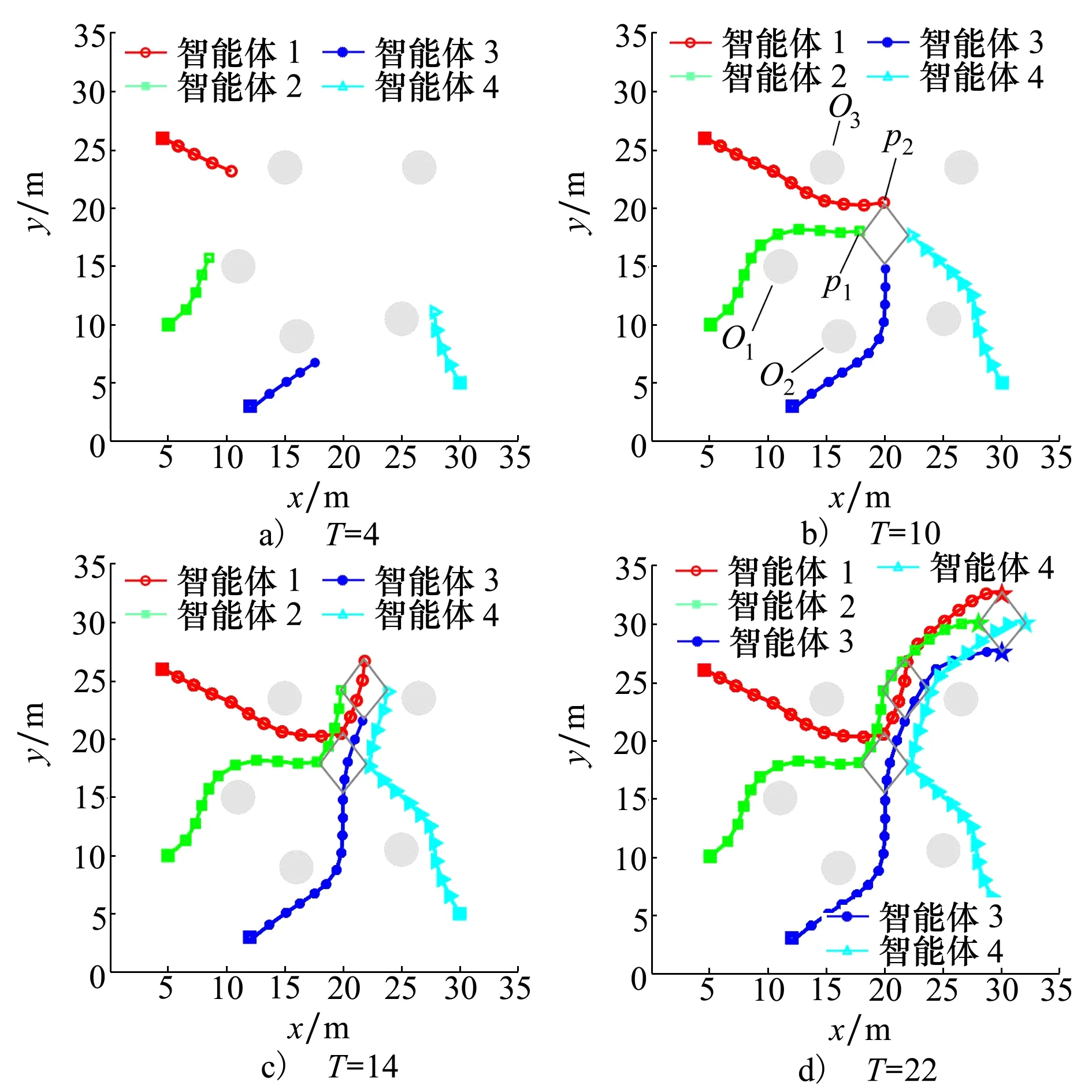
图7 多智能体编队控制过程运动轨迹(T表示步数)

在图7b)中,障碍物O1和O2之间的距离为7.8 m,不满足智能体2和智能体3之间9 m的避障要求,因此智能体无法穿越障碍物形成的狭窄通道,只能从两边绕行。相反障碍物O1和O3之间的距离为9.4 m,满足避障要求,因此智能体1和智能体2从障碍物中间通过。同时从图7b)中可以看出,智能体1选择p1位置的奖励最大,但是为了保证编队整体的性能最优,智能体1选择了p2位置,而智能体2选择了p1位置,验证了Nash均衡编队策略的有效性。图8描述了编队过程中智能体之间的距离变化,智能体之间的距离均满足设定的安全距离,在任务完成后智能体间的距离分别是4.9,3.9,3.1 m,符合设计的编队距离。

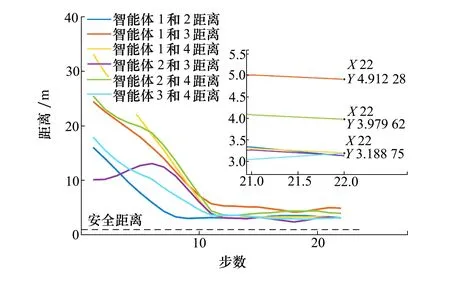
图8 智能体编队过程相互之间的距离

3.3 基于多无人机的编队任务实时性仿真

为了验证本文提出的迁移强化学习算法的实时性能和可靠性,基于Gazebo仿真平台,选用四旋翼无人机对算法有效性进行验证。硬件配置为英特尔i7-9700、GeForce RTX 3090,操作系统采用Ubuntu-18.04。场景大小设置为30 m×30 m,最大飞行速度v=1 m/s,飞行高度统一为2 m,8架无人机通过中心计算机共享全局信息,信息更新频率为10 Hz。如图9所示,不同形状的障碍物均可以抽象为长方体,因此用大小为1.5 m×1.5 m×2 m的长方体表示障碍物。预设无人机之间形成以坐标(15,15)为中心,半径为6 m的圆。

图9 不同障碍物的抽象表示

图10展示了无人机编队过程中关键时刻的截图,从图10a)可以看出无人机分2组从两边向着场景中心位置移动;图10b)中无人机通过障碍物形成的通道,进行避障飞行;图10c)中无人机形成初步聚集状态,但是无人机的航向没有统一,是杂乱无序的,不具备编队能力;图10d)中无人机的航向呈顺时针方向飞行,通过航向箭头可以看出,无人机均沿着设定圆的切线方向移动,从而验证了提出的算法能够使得无人机形成符合设定条件的圆形编队。图11展示了无人机的飞行轨迹曲线,形成符合条件的圆形轨迹。

图10 基于无人机的迁移强化学习算法仿真

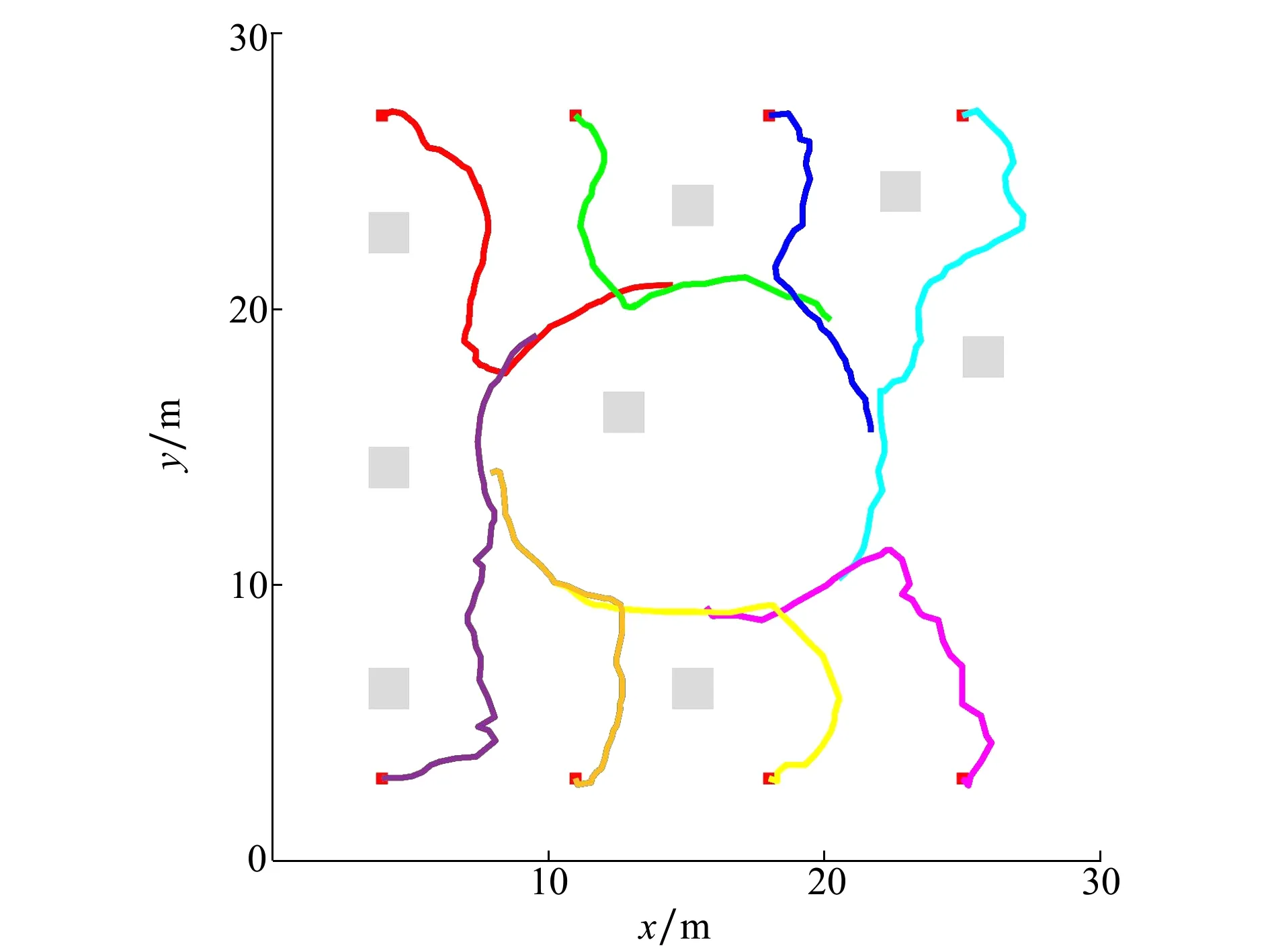
图11 无人机飞行轨迹

为了验证算法的实时性和可靠性,设计了多组实验,具体场景设置如表1所示,每组实验重复进行25次,并对数据进行统计分析。设定编队过程在120 s内完成,如果超出设定的时间阈值或者出现其他故障,则判定编队过程失败。通过分析编队形成的时间以及成功率,可以发现障碍物数量的增加对编队成功率的影响较小,当无人机的数量增加时,编队时间明显增加,同时成功率也降低。但是,4种场景的编队时间和成功率都在可接受的范围内,因此文章提出的算法具有较好的实时性和较高的可靠性。图12展示了4种场景中无人机形成圆形编队时的截图。

表1 基于迁移强化学习的无人机编队多种场景设置

图12 多种场景无人机的迁移强化学习算法仿真

4 结 论

针对复杂障碍环境下多智能体编队控制问题,本文提出了一种基于迁移强化学习的编队控制算法。基于设计的奖励函数,采用Nash均衡价值函数保证了多智能体编队系统的整体性能最优。利用值函数近似方法进行源任务学习,推导了权重更新公式,通过收敛性分析证明了参数更新呈指数收敛。在目标任务学习阶段,通过GMM算法对源任务进行聚类分析,基于康托洛维奇距离选择较优的源任务进行目标任务学习,避免了负迁移问题,提高了多智能体编队控制的效率。仿真实验对比分析了迁移前后的运动轨迹,证明了算法的有效性。通过编队任务仿真,实现了避障约束下的多智能体编队控制任务,在Gazebo平台,基于无人机模型进行了仿真分析,证明了算法的实时性和可移植性。未来的研究将设计更加精细的奖励函数,让奖励函数在接近最优解时大幅度增加,可以帮助学习算法快速收敛到最优解。考虑将本文提出的迁移学习算法从二维环境拓展到三维环境,模拟更加复杂的现实环境,同时通过时间约束或者增加燃料成本的惩罚来限制智能体的行动选择。