融入蜕变关系的杂交粒子群算法及在测试数据生成中的应用
2023-05-12焦重阳周清雷
焦重阳,周清雷
1(中国人民解放军战略支援部队信息工程大学,郑州 450001) 2(数学工程与先进计算国家重点实验室,郑州 450001) 3(河南信息工程学校,郑州 450000) 4(郑州大学 信息工程学院,郑州 450001)
1 引 言
软件测试用于发现和纠正软件中存在的错误和缺陷,是软件开发过程中一个必不可少的质量保证和验证的环节.美国国家标准与技术研究所的报告指出,软件测试可以减少超过三分之一的软件故障成本[1].但是,软件测试是一项耗时耗力的工作,它大约消耗了软件开发成本的50%[2].在软件测试中有着两个基本问题:oracle问题和可靠测试集问题[3].为缓解oracle问题,蜕变测试(Metamorphic Testing,MT)是一种有效的方法,越来越受到研究者们的关注,并检测出了大量的现实故障.蜕变测试的中心是一系列的蜕变关系(Metamorphic Relations,MR),这是目标函数在多个输入和它的预期输出方面的必要属性.在蜕变测试中,一些程序输入(源输入,Source Input)首先被生成为源测试用例,利用蜕变关系可以生成衍生输入(Follow-up Input)成为后续的测试用例.有效的测试数据可以发现软件中存在的错误,由于软件测试数据的设计和生成是非常耗时和错误率高的,如何有效快速的自动生成测试数据成为软件测试中研究的一个热点.多年来,为了解决可靠测试集的问题,许多研究者提出了不同的方法来自动生成测试数据.其中,基于搜索的软件测试(Search Based Software Testing,SBST)[4]方法具有自动化、智能化、高效等优点,引起了广大学者们的关注和研究.
粒子群算法作为一种群体智能搜索算法,因算法规则简单、容易实现、收敛速度快以及可调节参数少等优势,在工程应用中颇为广泛.目前,将粒子群算法应用于测试数据自动生成中已有很多的研究,如张娜等[5]提出了一种基于反向学习与再次搜索的粒子群优化算法用于测试用例生成;Sahoo等[6]提出了一种新的适应度函数计算方法,通过覆盖关键路径生成测试用例实现最大的路径覆盖;董跃华等[7]提出了一种基于离散度大小的动态调整粒子群参数的优化算法并将该算法应用于测试数据生成.Wang等[8]为了提高PSO的性能,提出了一种改进的PSO生成测试用例;Molaei等[9]将遗传算法与粒子群算法相结合,提出了基于增强学习策略引导粒子群的学习,采用交叉操作将粒子群变异,该算法在精度方面和收敛速度方面具有更大的优势.
以上研究中针对提高目标路径的测试数据生成的效率做了很多研究,但都不涉及程序自身的固有属性,本文利用待测程序的自身性质构造出程序的蜕变关系,提出了融入蜕变关系的杂交粒子群算法(Hybrid Particle Swarm Optimization Algorithm With Metamorphic Relations,MRHPSO),找出覆盖多条路径的测试数据,进一步提高了测试数据生成的效率.本文为提高算法的进化速度,提出了自适应的惯性权重的调节方案,即根据全局最优点的距离进行动态调整;为避免粒子群算法陷入局部极值,呈现早熟性,将遗传算法的杂交思想引入粒子群算法中,提出了杂交粒子群算法;为找到多条路径覆盖的测试数据,融入待测程序的蜕变关系.后续的测试数据能够利用待测程序的蜕变关系生成,节省了大量的测试时间.通过实验结果表明,本文所提出的方法在收敛速度和生成多路径的测试数据上有明显优势.
2 标准粒子群算法
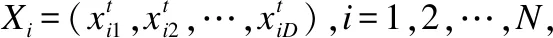
(1)
(2)
其中,w为惯性权重;c1和c2为学习因子,也称加速常数,代表粒子向优秀个体学习能力的大小;r1和r2为介于0和1之间的均匀随机数,增加了粒子飞行的随机性.
从公式(1)可以看出,粒子的移动速度是在三方面的共同作用下进行迭代更新的.第1部分代表粒子的惯性功能,表示前一次速度值对当前速度的影响;第2部分代表粒子的自身认知功能,根据自身的经验进行学习;第3部分代表粒子的社会学习功能,粒子向整个种群中的最优粒子学习,反映了粒子间的协同合作和知识共享.
3 MRHPSO算法及在测试数据生成中的应用
3.1 惯性权重w的自适应调节方案
惯性权重是指粒子能保持前一时刻运动状态的能力,设计良好的惯性权重能推动粒子在合适的时机进行适当的探索,并在整体上保持前期搜索速度较快,后期搜索速度较为缓慢的节奏.从粒子更新公式可以看出,惯性权重值越大,算法的全局搜索能力越强;惯性权重值越小,算法的局部搜索能力越强,越有利于提高搜索精度.总体来看,惯性权重依然是平衡粒子群算法全局和局部搜索能力的重要参数之一,在一定程度上决定了算法性能的优劣.目前采用较多的动态惯性权重是Shi等[12]提出的线性递减权值策略.
(3)
其中,wmax和wmin分别表示惯性权重最大值和最小值,通常为0.9和0.4,t表示当前迭代次数,T表示最大进化代数.
此方法解决了基本PSO算法容易早熟及后期在全局最优解附近产生振荡的现象.研究者们发现控制参数惯性权重w的设置效果不但和进化代数有关而且和全局最优值的位置也有关系.所以,本文提出惯性权重w的调整如公式(4)所示:
(4)
其中,f表示粒子实时的函数适应度函数值;fmin表示当前所有粒子最小适应度函数值;favg表示当前所有粒子的平均适应度函数值.
(5)
其中,N表示种群规模;fi表示第i个粒子的适应度函数值.
3.2 杂交粒子群算法
为解决粒子群算法在后期易陷入局部极值,本文在粒子群算法中融入遗传算法的杂交操作,提出了杂交粒子群算法(Hybrid Particle Swarm Optimization algorithm,HPSO).HPSO的主要思想是:在粒子群每次进化的过程中,首先,根据设定的杂交概率取出一定数量的父代粒子(m)放入杂交池内;然后,在杂交池中,对被取出的一定数量的m两两任意进行交配,形成一样数量的子代粒子(n);最后,利用n代替m.
子代粒子的位置如公式(6)所示:
nx=i×mx(1)+(1-i)×mx(2)
(6)
其中,nx为子代粒子的位置;mx为父代粒子的位置;i为介于0和1之间的均匀随机数.
子代粒子的速度如公式(7)所示:
(7)
其中,nv为子代粒子的速度;mv为父代粒子的速度.
3.3 蜕变关系
定义1.蜕变关系:设f为目标函数,程序p实现函数f的功能,假设程序有两个以上的输入
若
r(x1,x2,…,xn)⟹rf(f(x1),f(x2),…,f(xn))
(8)
则称(r,rf)为程序p的蜕变关系.
若程序p是正确的,则它一定满足:
r(I1,I2,…,In)⟹rf(P(I1),P(I2),…,P(In))
(9)
其中,I1,I2,…,In是程序p的对应于x1,x2,…xn的输入,p(I1),P(I2),…,P(In)是相应的输出.
定义2.蜕变域(DMT(p))与非蜕变域(DNMT(p)):假设D(D′⊆D)是程序p的输入域,在D′上对p进行蜕变测试,则称D′是p的蜕变域,记作DMT(p),称D-D′为程序p的非蜕变域,记作DNMT(p).
定义3.源输入和衍生输入:假设(r,rf)是程序p的蜕变关系,若r是一个二元等式关系(r(x1,x2)),则称(r,rf)是程序p的二元蜕变关系,记作(rb,rfb).若对于∀I1∈ξ⊆DMT(P),∃I2∈ξ⊆DMT(P),使得rb(I1,I2)成立,则称ξ是二元蜕变关系(rb,rfb)的定义域,记作DR((rb,rfb)),称I1为源输入,I2为I1基于(rb,rfb)的衍生输入,记作I2=FU(I1,(rb,rfb)).
例如,在测试计算函数f(x)=e-x的程序时,依照定义2,pe-x的蜕变域DMT(pe-x)=(-∞,+∞).MRe-x:(x1+x2=0,f(x1)×f(x2)=1)是根据目标函数的ex×e-x=1这一性质,为pe-x构造的一条二元蜕变关系,依照定义3,MRe-x的定义域DR(MRe-x)=(-∞,+∞),任选一值0.2∈DR(MRe-x)作为源输入,基于MRe-x的衍生输入FU(0.2,MRe-x)=-0.2.
3.4 适应度函数构造方法
针对路径覆盖方法生成测试数据,主要是给出程序在实参的驱动下实际遍历的路径和分支路径之间的偏离程度.适应度函数构造的目标是它能够很好地评价所生成的测试数据的优劣,并且能引导粒子群最终找到目标路径的测试数据.所以,适应度函数的构造是搜索算法自动生成测试数据效率高低的关键.
本文参考Korel[13]和Tracey等[14]的理论研究成果,适应度函数的设计采用“分支函数叠加法”.所有的分支谓词都是“E1OPE2”的形式,其中,E1和E2表示算术表达式.OP∈{<,<=,>,>=,=,≠}.相应的目标函数是“frel0”的形式,其中,f是一个实值函数,即“分支函数”.采用如表1所示的分支谓词和分支函数的关系.
其中,逻辑运算采用如表2的构造方法(Bi表示分支谓词,Fi为相应的分支函数).
假设由m个分支,n个参数组成目标路径,则m个分支函数分别表示为:
f1=f1(x1,x2,…,xn)
f2=f2(x1,x2,…,xn)
…
fm=fm(x1,x2,…,xn)

表1 分支函数的构造方法Table 1 Connection between branch predicates and branch functions
该路径的适应度函数表示为:
F=F(f1)+F(f2)+…+F(fm)
(10)
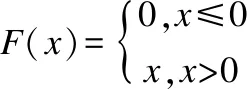

表2 逻辑运算符的构造方法Table 2 Information for processing logical operators
3.5 MRHPSO算法自动生成测试数据的模型
本文提出的MRHPSO算法生成测试数据模型主要包括3个模块,如图1所示:测试环境的构造模块、基于HPSO算法的测试数据生成模块和基于MR的测试数据生成模块.

图1 MRHPSO算法生成测试数据的模型Fig.1 Framework of the proposed method
测试环境构造模块是该模型的基础模块.在此模块,对待测程序进行静态路径分析,选择目标路径,构造出适应度函数并构建蜕变关系.基于HPSO算法的测试数据生成模块是该模型的重要组成部分.根据HPSO算法的具体流程生成源测试用例.基于MR的测试数据生成模块是该模型的核心部分.根据所构造的蜕变关系利用源测试用例生成新的测试数据.当基于MR生成的所有衍生输入都无法遍历路径时,该算法将结束.
3.6 MRHPSO自动生成测试数据的算法流程
输入:经分支函数插桩后的待测程序
输出:找到目标路径的测试数据
Step 1.对待测程序进行静态分析,插装待测程序,构造蜕变关系.
Step 2.对粒子群进行初始化,设定种群规模N的值、学习因子c1、c2的值和惯性权重的最大值wmax和最小值wmin,以及最大进化代数T.在数据范围内,对每个粒子随机初始化它们的位置Xi和速度vi.
Step 3.对进化个体进行解码,执行插桩后的待测程序.
Step 4.首先,找到目标路径的测试数据,保存此测试数据并将该目标路径从目标路径集中去除;然后,如果此测试数据(源输入)范围不在非蜕变域DNMT(p)中,那么,根据MR生成新的测试数据(衍生输入);最后,判断衍生输入是否在预定义的数据范围内且是否覆盖了目标路径集中的路径,如果是,则保存该测试数据,并将此路径去除.
Step 5.对每个粒子计算适应度值F(xi),将粒子的位置和适应值存储在粒子的个体极值Pbest(i)中,将全部Pbest中适应度值最好的粒子的个体位置和适应度值存储在全局极值gbest中.
Step 6.根据公式(4)自适应调节惯性权重,根据粒子群进化公式(1)、公式(2),生成子代进化种群.
Step 7.对每个粒子,用它的适应度值F(xi)与个体极值Pbest(i)进行比较.如果F(xi) Step 8.按照HPSO算法的主要思想,根据公式(6)和公式(7)更新子代种群. Step 9.判断终止条件是否得到满足,若是,则输出测试数据;否则,返回Step 3. 本文采用三角形分类程序(TriClassArea)、求最大最小值程序(MaxMin)和冒泡排序程序(BubbleSort)作为基准程序,分析比较本文所提出的算法(MRHPSO)与自适应粒子群算法(APSO)在数据自动生成上的性能.被测程序TriClassArea的功能是:判断输入的3条边a,b,c是否均大于零且满足构成三角形的条件,若满足,则将所构成的三角形类型输出并计算三角形的面积.三元组(a,b,c)分别表示三角形的三条边,作为程序的源输入,三角形类型和面积作为程序的结果输出.该程序有多个条件控制,但不包括循环结构,共有6个分支,含有3个选择嵌套.被测程序MaxMin的功能是:输出3个数中的最大值和最小值.该程序有2个选择构成选择并列关系.被测程序BubbleSort的功能是:10个数由小到大顺序输出.该程序共有2个循环,1个选择.每组实验操作100次,分析两个重要指标:平均进化代数和平均进化时间.在实际实验中,存在找不到目标路径测试数据的情况,记录100次重复实验能够搜索到测试数据的平均成功率. 蜕变关系是蜕变测试的重要组成部分,且不具有通用性,决定了蜕变测试的有效性[15].蜕变关系的构造需要根据程序的特定属性,通常需要测试人员有一定的先验知识.根据三角形的性质可知:DMT={(a,b,c)|(a+b>c∧(a+c>b)∧(b+c>a))}为TriClassArea程序的蜕变域.依据三角形的性质和平行四边形的性质为待测程序TriClassArea构造出6条蜕变关系,分别为MR1—MR6.其中,(a,b,c)表示源输入,(a′,b′,c′)表示衍生输入,TriClassArea(a,b,c)表示3个边长分别为a,b,c的三角形的面积.根据数组中任意两个元素进行交换,程序结果输出不变的性质为待测程序MaxMin构造出2条蜕变关系,分别为MR7—MR8.待测程序BubbleSort和MaxMin程序有相同的蜕变关系.通常,一个程序的源输入的衍生输入有不同的价值,可能覆盖不同路径.一个蜕变关系的输入关系可以用来生成覆盖多个路径的测试用例.假设输入x所遍历的路径与-x不同,当生成测试用例x时,另一个测试用例-x由蜕变关系生成. MR1:If (a′,b′,c′)=(b,a,c),thenTriClassArea(a′,b′,c′)=TriClassArea(a,b,c) MR2:If (a′,b′,c′)=(c,b,a),thenTriClassArea(a′,b′,c′)=TriClassArea(a,b,c) MR3:If (a′,b′,c′)=(a,c,b),thenTriClassArea(a′,b′,c′)=TriClassArea(a,b,c) MR7:如果数组中任意两个不同值的元素进行交换,程序输出结果相同. MR8:如果将数组中的所有元素逆序排列,程序输出结果相同. 图2 程序TriClassArea蜕变关系的构造原理Fig.2 Aufbau principle of metamorphic relations based on TriClassArea 本文提出的MRHPSO算法,在用杂交粒子群算法产生测试数据的过程中,对找到的测试数据通过蜕变关系衍生出覆盖其他目标路径的测试数据.使待测程序的路径改变的蜕变关系(MR)和非蜕变域(DNMT(p))如表3所示. 表3 路径改变的蜕变关系Table 3 Metamorphic relations of the program 4.3.1 硬件环境 系统处理器:Intel(R)Core(TM)i5-8500 CPU @ 3.00GHz 3.00GHz; RAM:8.00GB. 4.3.2 软件环境 操作系统:Windows 10专业版; 实验平台:MATLAB R2016b; 开发语言:Matlab. 为避免算法参数的配置不同对算法性能有所影响,两种算法采用相同的参数配置.被测程序相同的参数设置如下:最大进化代数T=1000,学习因子c1=1.5,c2=1.5,惯性权重wmax=0.65,wmin=0.15.杂交概率bc=0.8,杂交池比例bs=0.1. 4.4.1 TriClassArea程序 针对不同种群规模下,不同数据范围下的三角形整数边运行100次实验,记录覆盖目标路径的测试数据所需的进化代数和运行时间,实验结果如表4、表5和表6所示. 表4 测试数据生成效率实验结果Table 4 Comparison of two algorithms 表5 测试数据生成效率实验结果Table 5 Comparison of two algorithms 从表4可以看出:当粒子群规模为100时,在4种不同的数据范围下,MRHPSO算法均比APSO算法的平均进化代数少、平均进化时间短;随着数据范围的不断增大,生成测试数据的难度也随着增加,两种算法的平均进化代数和平均进化时间均不断增多,但MRHPSO算法在4种数据范围的实验结果总是APSO算法的平均进化代数少、平均进化时间短.如在数据范围为[1,256],APSO算法的进化代数平均为167.1代,而MRHPSO算法的进化代数平均只需54.5代,约是APSO算法的1/3.与此相对应,APSO算法的平均进化时间3.1811s,而MRHPSO算法的平均进化时间只需2.3331s. 表6 测试数据生成效率实验结果Table 6 Comparison of two algorithms 从表5、表6不难看出:在种群规模为200和300的情况下,针对4种数据范围,MRHPSO算法总是比APSO算法的平均进化代数少,平均进化时间短.随着种群规模的增多,测试数据生成所需要平均进化时间也增多.如在种群规模为300时,数据范围在[1,512]的情况下,平均进化代数MRHPSO算法比APSO算法少118.2代,约为APSO算法的1/3.相应地,MRHPSO算法的平均进化时间比APSO算法少0.5755s. 图3 生成测试数据的平均成功率Fig.3 Success rate of test data generation 图3为两种算法生成测试数据的平均成功率,从图3中可以看出,当数据范围加大时,APSO算法的生成测试数据的平均成功率有所下降.如在数据范围为[1,1024]时,MRHPSO算法平均成功率达到100%,而APSO算法的平均成功率为99%,说明随着数据范围的增大,MRHPSO算法更具有优势. 4.4.2 MaxMin程序 在种群规模为100的情况下,针对不同数据范围下的3个整数运行100次实验,记录覆盖目标路径的测试数据所需的进化代数和运行时间,实验结果如表7所示. 表7 测试数据生成效率实验结果Table 7 Comparison of two algorithms 4.4.3 BubbleSort程序 在种群规模为100的情况下,针对不同数据范围下的10个整数运行100次实验,记录覆盖目标路径的测试数据所需的进化代数和运行时间,实验结果如表8所示. 表8 测试数据生成效率实验结果Table 8 Comparison of two algorithms 从表7、表8不难看出:种群规模100的情况下,在不同的数据范围下,MRHPSO算法在寻找目标测试路径时所需的进化代数和所消耗的进化时间上均少于APSO算法. 在不同的种群规模下,如200,300,400等情况做了大量的实验,实验结果均显示,MRHPSO算法在进化代数和进化时间上均优于APSO算法. 通过对比实验表明,本文所提出的方法能有效的提高测试数据生成的效率. 手工测试过程消耗了软件开发的40%~70%的时间和成本.自动的生成测试可以有效降低测试成本,提高测试质量,而测试数据的好坏直接决定软件测试的结果,因此,如何生成高质量的测试数据一直是研究人员关注的重点.本文提出了融入蜕变关系的杂交粒子群算法并将其应用于测试数据生成中,利用测试数据之间的蜕变关系,在进化生成过程中,当有一个目标路径测测试数据生成时,作为源输入,利用待测程序的蜕变关系衍生出后续的测试数据,以覆盖程序的其他目标路径,使得测试数据的生成效率得到提高.但是,本文方法只适用于能够根据待测程序的本质属性构造出有效的蜕变关系的这种情况,需要测试人员有一定的先验知识.今后的工作中,继续将提高测试数据自动生成的效率作为主要的研究方向.4 实 验
4.1 实验方案
4.2 蜕变关系的构造
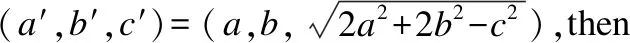

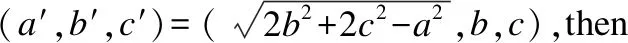
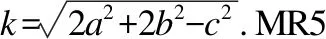
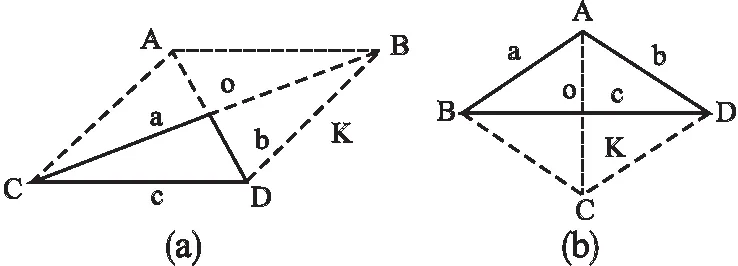

4.3 实验环境和参数设置
4.4 实验结果



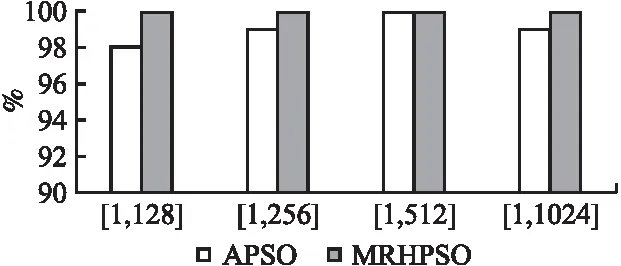
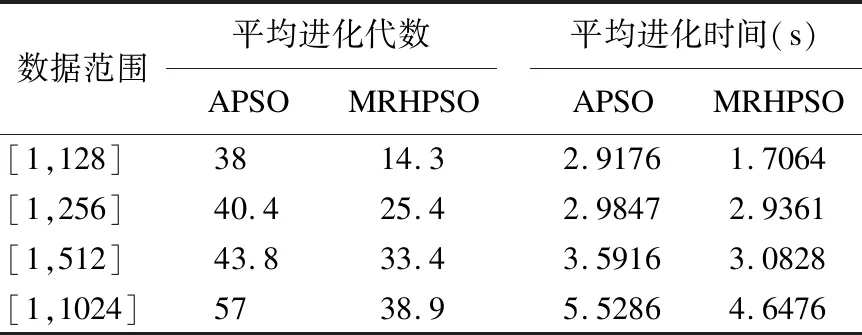

5 结 论
