具有不充分信息的高维时间序列因果关系网络研究
2023-05-12王双成赵大平
王双成,郑 飞,赵大平
1(上海立信会计金融学院 信息管理学院,上海 201620) 2(上海立信会计金融学院 数据科学交叉研究院,上海 201209) 3(上海立信会计金融学院 国际经贸学院,上海 201620)
1 引 言
人类对现实世界中现象的一种强烈渴望就是因果联系,从古至今人们不间断地从不同层次和角度探索因果理论和发现因果关系的方法,以达到更好地认识和改造世界的目的.早期的因果关系属于哲学的范畴,现代更强调从数据中的因果关系发现.时间序列是现实世界数据的重要表现形式之一,对时间序列已有许多研究,如胡衍坤[1]、杨超[2]和任守纲[3]等.在宏观经济与金融等领域,数据主要以时间序列的形式存在,大量宏观经济与金融时间序列真实地记录了系统在不同时间点(或时间片)的各种重要信息,其中蕴含着丰富而有价值的因果关系和映射规则等方面的知识,这些知识往往是诊断宏观经济与金融体系运行情况,揭示经济运行规律,以及制定相应的调控政策的重要依据.具有不充分信息的时间序列数据普遍存在,对其进行因果建模和信息传递计算也有着广泛的需求.关于时间序列变量的因果关系研究主要从两个方面展开,分别是连续变量(或数据)和离散变量(或数据)的因果关系,它们各有优势与不足,并具有互补性.
对连续数据的因果关系研究主要采用回归计算和检验的方法,如David[4]采用广义回归发现因果关系,Ryutah[5]使用线性分位数回归研究因果关系,Luo[6]依据逐步回归的因果效应分析,Maxim[7]关于全球化与转型后欧盟国家社会经济发展的面板因果关系和回归分析,Rothenhusler[8]采用锚回归(Anchor regression)研究因果关系.这些因果关系发现(或检验)方法所依据的是逐步回归计算和对回归的贡献,往往具有较强的经济学含义,但一般是针对特定的问题和具体的方面.
关于离散数据因果关系的研究一般采用贝叶斯网络(Bayesian network)[9]或动态贝叶斯网络(Dynamic Bayesian network)[10]方法.贝叶斯网络[1]是通过条件独立性(或概率分布)来描述随机变量(简称为变量)之间的影响与制约关系的有向概率图模型,在许多领域都得到了广泛的应用.它由结构(有向无环图)和参数(条件概率分布表)两部分构成,其结构中弧的方向具有因果语义[10],因此是研究因果关系的有力工具,基于贝叶斯网络进行时间序列变量因果建模与分析是一种发展趋势,这种贝叶斯网络一般也被称为因果图或因果关系网络(本文采用这种称呼).对贝叶斯网络已有许多研究,主要集中在贝叶斯网络学习、贝叶斯网络推理和贝叶斯网络应用3个方面,如Constantinou[11]、Caravagna[12]和王双成[13]等的贝叶斯网络学习研究,Mitchell[14]、Zhang[15]和Jorge[16]等的贝叶斯网络推理研究,Li[17]、Yan[18]和Wang[19]等的贝叶斯网络应用研究等,但这些贝叶斯网络研究是针对非时间序列数据.
动态贝叶斯网络[10,20]是贝叶斯网络的扩展,可用于解决与时间有关的不确定性问题.1998年Friedman给出受平稳性与马尔可夫性两个假设约束的动态贝叶斯网络定义和基于打分-搜索的学习方法,2002年Murphy比较系统地论述了动态贝叶斯网络的理论、方法和应用,从此揭开了动态贝叶斯网络的研究进程.早期的动态贝叶斯网络主要关注的是隐马尔科夫模型(Hidden Markov model)、卡尔曼滤波模型(Kalman filtering model)和两个模型的变体,以及它们在语音识别、视频分析和信息滤波等方面的应用研究.目前,对动态贝叶斯网络的研究主要从3个方面展开,分别是Friedman动态贝叶斯网络的变体、减弱平稳性和马尔科夫性两个假设,以及动态贝叶斯网络的应用,如Liu[21]、Harries[22]和Zakaria[23]等对变体的研究,Wu[24]、Shafiee[25]和Qiu[26]等对减弱两个假设的研究,王双成[27-31]和Liu[32]等的应用研究.建立这些动态贝叶斯网络均需要大量的面板数据或时间序列数据,对高维小样本时间序列情况不具有实用性.
近些年,对因果关系的研究是一个热点,这些研究主要面向非时间序列数据,并从两个方面展开,一个方面是如何建立因果关系网络(因果关系网络学习),另一个方面是局部因果推断.本文研究高维小样本时间序列数据的因果关系网络学习与因果影响计算,采用主流的搜索-打分方法建立因果关系网络,并将把经典的统计抽样方法与机器学习分类思想相结合的抽样分类技术用于变量之间的信息传递和影响计算.
本文的主要贡献如下:
1)当时间序列数据集中所蕴含的信息不充分时,采用一般的依赖分析或搜索-打分方法所建立的因果关系网络结构的可靠性无法得到保障,本文首先将汇聚结构与似然函数相结合,提出了汇聚递减变量排序方法,在变量排序的基础上,通过局部贪婪搜索-打分进行因果关系网络结构,可降低对数据量的需求,并能够提高学习效率和可靠性.
2)具有不充分信息时间序列数据的因果关系网络学习,不可避免地会丢失一些弱因果关系,从而损失部分传递信息,本文通过建立信息提取变量来获取压缩的变量组信息,以弥补由弱因果关系的缺失所导致的传递信息丢失和实现高维数据的降维,并提出基于递归汇聚结构和后验分布抽样识别准确率的信息传递计算方法.
3)基于递归汇聚结构和后验分布抽样识别准确率,本文分别给出了时间序列变量之间的影响程度计算、影响的敏感性计算和汇聚与扩散影响计算方法,而且还具有明显的语义,并使用宏观经济时间序列数据进行了相应的实验验证与分析.
文章分为5个部分,第1部分对贝叶斯网络和动态贝叶斯网络的发展进行回顾与分析;第2部分是时间序列变量之间的因果关系网络学习;第3部分给出了时间序列变量之间的信息传递计算方法;第4部分是使用宏观经济时间序列数据进行的实验与分析;第5部分是结论和进一步的工作.时间序列变量之间的因果关系研究需要解决两个问题,一个是时间序列变量之间的因果关系网络学习,另一个是时间序列变量之间的信息传递计算,本文以宏观经济指标时间序列数据为背景,研究具有不充分信息的高维时间序列因果关系网络.另外,文中将概率模式中的变量和图形模式中的结点有时不加区分,对变量、因素和指标有时也不加区分.
2 高维时间序列变量的因果关系网络学习
针对具体情况和实际需求,我们将高维时间序列分成两部分,一部分是核心时间序列(根据专业知识确定),另一部分是外围时间序列;在时间序列数据预处理的基础上(包括缺失值处理和离散化),对于核心时间序列,需要建立因果关系网络;而关于外围时间序列,由于时间序列较多,首先根据专业领域知识(或聚类算法)进行分组,然后建立每一个组的信息提取变量,最后将所有信息提取变量融入核心时间序列的因果关系网络,从而可实现高维时间序列变量的降维.使用X1[t],X2[t],…,Xn[t]表示具有离散值的时间序列变量,x1[t],x2[t],…,xn[t]是具体的取值,D[n,T]={x1[t],x2[t],…,xn[t]|1≤t≤T}表示具有n个时间序列变量和T个记录的时间序列数据集.
2.1 核心时间序列变量的因果关系网络学习
虽然有许多方法可用于时间序列的因果关系网络学习,但对于具有不充分信息的时间序列数据,本文结合变量排序和具有代表性的局部贪婪搜索-打分进行核心时间序列变量的因果关系网络学习,学习过程包括变量排序、因果关系网络结构学习与因果关系网络参数学习3个部分.
1)变量的排序
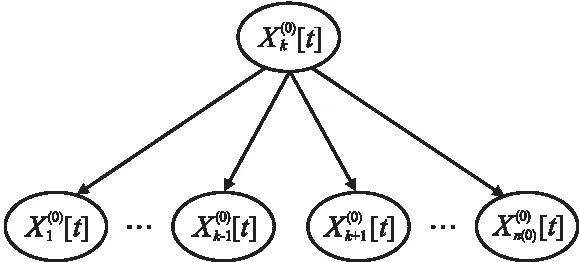
图1 以为父结点的汇聚结构Fig.1 Aggregation structure with as parent node
根据似然函数的定义和和图1中的条件独立性关系,可以得到:
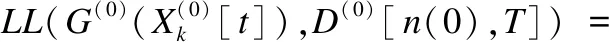
(1)
算法1.核心变量组中变量的排序
输入:时间序列数据集D(0)[n(0),T]
输出:核心变量组中变量的顺序
1.Forv=1 ton(0)-1
2. 计算1+n(0)-v个变量的似然打分
3. 在其中选择具有最大似然打分的变量排在第v个位置
4.End for
5.将最后一个变量排在n(0)的位置,得到核心变量组中变量的顺序
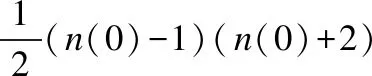
2)因果关系网络学习
算法2.核心变量组的因果关系网络学习
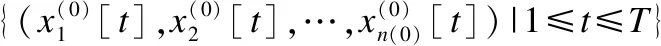
输出:核心变量组的因果关系网络(包括结构和参数)
1.Fori=2 ton(0)
2. Fork=1 to Δ//Δ为父结点的最大数量
5. Else
6. Exit for
7. End if
8. End for
9.End for
10.基于最大似然方法估计因果关系网络中的参数
11.得到核心变量组的因果关系网络
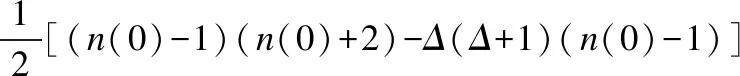
2.2 外围时间序列变量的信息提取变量学习
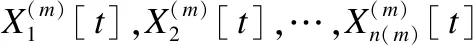
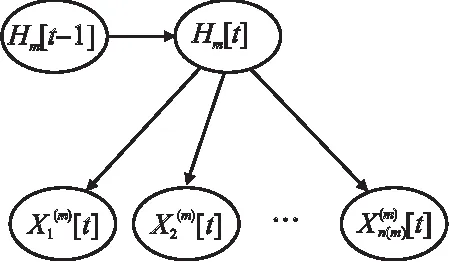
图2 第m个外围变量组的信息提取变量局部结构Fig.2 Local structure of information extraction variable for the m-th peripheral variable group
根据概率公式和图2中的条件独立性关系,可以得到:
(2)
其中α是与Hm[t]无关的量.
对(2)式进行归一化处理,记:
ω(j)=
对生成的随机数λ,变量Hm[t]的修正值为:
(3)
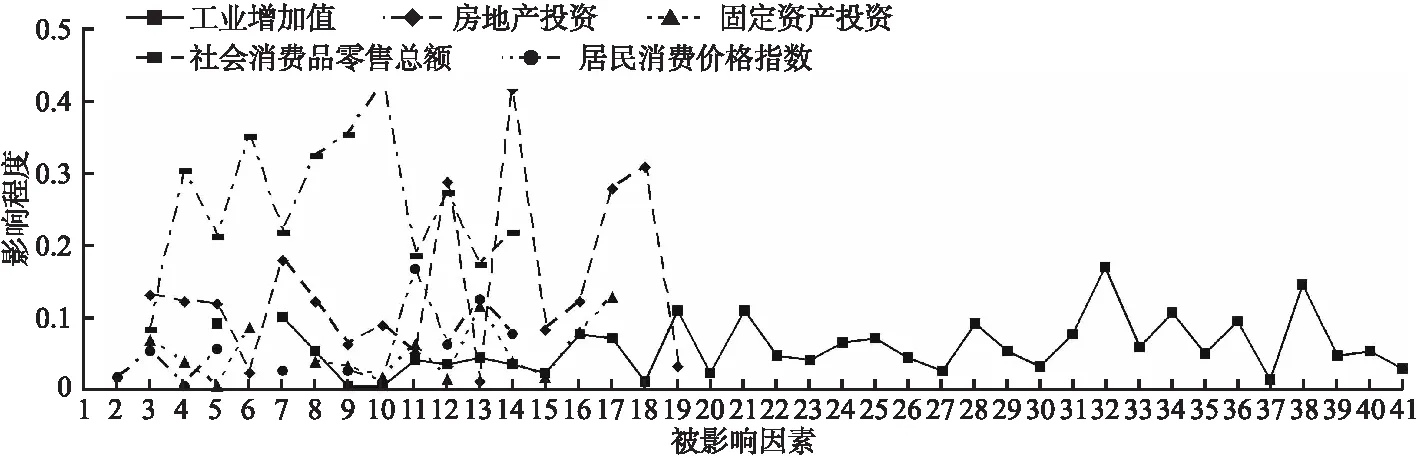
其中1 算法3.第m组外围变量的信息提取变量学习 输出:信息提取变量数据集{hm[t]|1≤m≤M,1≤t≤T} 3.Forv=1 toV∥迭代次数循环,V是最大迭代次数 4. Fort=1 toT∥数据集记录循环 5. 估计p(hm[t])和p(hm[t]|hm[t-1]) 6. Fork=1 ton(m)//组内变量循环 8. End for 12. End for 13.End for 14.得到信息提取变量时间序列数据集{hm[t]|1≤t≤T} 信息提取变量学习算法的主要运算是条件概率估计,对每一个信息提取变量值的修正需要进行n(m)+2次的概率估计,修正完T个信息提取变量值实现一次迭代,达到V次结束迭代,因此,相对于条件概率估计,算法的时间复杂度是O(VTn(m)).用D[n+M,T]表示具有信息提取变量的数据集. 在因果关系网络学习的基础上,本文基于后验分布抽样识别准确率进行时间序列变量之间的信息传递计算. 图的影响因素局部结构Fig.3 Local structure of influencing factors for accuracy(sampling,X[t],Ω(X[t]),D[n,T]) (4) 其中: 可以将Ω(X[t])和X[t]分别看做属性和类,那么accuracy(sampling,X[t],Ω(X[t]),D[n,T])便是基于分布抽样的分类准确率,相对于经典的依据最大似然的分类准确率(易于出现极端化情况)能够更好地传递分布信息,而且关于分类的理论也均可被应用. 当accuracy(sampling,X[t],Ω1(X[t]),D[n,T])> accuracy(sampling,X[t],Ω2(X[t]),D[n,T])时,Ω1(X[t])能够比Ω2(X[t])为X[t]提供更多的分类信息,也就是Ω1(X[t])向X[t]传递的信息比Ω2(X[t])向X[t]传递的信息量大,这样,便可以通过抽样识别准确率来计算和比较时间序列变量之间的信息传递. 在信息传递计算的基础上,进行时间序列变量之间的影响计算,包括影响程度计算、敏感性计算和汇聚与扩散影响计算,这些计算可为决策提供支持. 1)影响程度计算 (5) 其中Φ表示空集. 2)敏感性计算 (6) 其中Dbefore_disturbance[n,T]和Dafter_disturbance[n,T]分别是关于Z[t]的扰动前和扰动后时间序列数据集. 3)汇聚与扩散影响计算 (7) (8) 本文从国家数据网站下载宏观经济指标时间序列数据,按照国家数据网站的布局进行时间序列变量(指标)分组,采用滑动平均的方法修复稀疏的丢失数据,对成段的丢失数据则用随机数填充(不增加信息,也尽量避免引入噪声),使用差分的方法去除时间序列的单调性,依据时间序列的增减变化对其进行离散化,分别从因果关系网络结构学习、信息提取变量学习的迭代收敛性、变量之间的影响程度计算、变量之间的敏感性计算和汇聚与扩散影响计算5个方面进行实验与分析. 根据数据量、内容的重复性和内容的重要性等选择24个宏观经济指标时间序列数据集,关于时间序列数据集的具体情况如表1所示. 表1 宏观经济指标时间序列数据集Table 1 Time series data set of macroeconomic indicators 本文只给出房地产投资数据集的因果关系网络结构(取Δ=4).房地产投资数据集排序后的指标为:商业营业用房竣工面积(X1[t])、商业营业用房施工面积(X2[t])、商品住宅竣工面积(X3[t])、商品住宅施工面积(X4[t])、办公楼施工面积(X5[t])、本年实际到位资金合计(X6[t])、房地产竣工面积(X7[t])、房地产施工面积(X8[t])、商品房销售面积(X9[t])、商品住宅销售额(X10[t])、办公楼销售面积(X11[t])、办公楼销售额(X12[t])、房地产业土地成交价款(X13[t])、商品住宅销售面积(X14[t])、房地产业土地购置面积(X15[t])、商业营业用房销售额(X16[t])、商业营业用房销售面积(X17[t])、商品房销售额(X18[t])和办公楼竣工面积(X19[t]),均是累计增长率,19个指标之间的因果关系如表2和图4所示. 由于房地产投资数据集中只有231个记录,因此无可避免地会导致一些因果关系的丢失,但通过与经济领域的专家交流,他们认为图4比较好的反映了主要的因果关系,还有一些因果关系超出了经验的范畴,具有理论和实际意义,适合于小样本时间序列数据的因果关系网络结构学习.在24个宏观经济指标时间序列数据集中许多因果关系网络结构并不连通,因果关系网络结构由几部分构成,还有存在孤立点或孤立因果关系弧的情况. 表2 房地产投资数据集的父子结点情况Table 2 Parent child nodes of real estate investment data set 图4 房地产投资因果关系网络Fig.4 Causality network of real estate investment 信息提取变量学习迭代的收敛与否会影响变量组所蕴含信息的提取效果,本文结合递归汇集结构和Gibbs抽样进行信息提取变量的递进迭代学习,迭代次数V=40,收敛检验阈值ε=0.05,工业增加值、房地产投资、固定资产投资额、社会消费品零售总额和居民消费价格指数5个数据集的信息提取变量学习迭代情况如图5所示,其中横轴表示迭代次数,纵轴表示相邻两次迭代非一致数据的比例. 从图5中我们能够发现,经过20次迭代后,非一致数据比例均小于5%,没有出现大幅度的波动,这说明信息提取变量的结构与数据中所蕴含的结构具有相容性,而且能够实现通过信息提取变量对变量组数据集中信息的提取,其它变量组的信息提取变量学习迭代也具有类似的情况. 图5 信息提取变量学习迭代的收敛情况Fig.5 Convergence of learning iteration for information extraction variables 本文基于后验分布抽样识别准确率进行时间序列变量之间的影响程度计算,具体的计算方法见公式(5).分别使用工业增加值(同比增长率)、房地产投资(累计增长)、固定资产投资(累计增长)、社会消费品零售总额(同比增长)和居民消费价格指数(上年同月)5个数据集进行影响程度计算.在对一个变量的影响计算中,本文首先计算这个变量的马尔科夫毯(核心变量马尔科夫毯)中变量的影响,然后再分别计算当给定马尔科夫毯中变量时,其它核心变量的信息提取变量、时滞变量(所有核心变量的时滞变量)和外围变量组的信息提取变量的影响,再计算3种情况影响与马尔科夫毯中变量影响的差值,最后得到在给定马尔科夫毯中变量时的影响程度,具体情况如表3所示. 表3 影响程度统计表Table 3 Statistical table of impact degree 从表3中能够发现,当给定马尔科夫毯中变量时,3种情况的平均值均大于0,这说明补充信息提取变量、时滞变量和外围信息提取变量均能提供额外的正向识别信息,有利于提高识别准确率,5个数据集的平均影响程度依次是0.0036(补充信息提取变量)、0.0114(时滞变量)和0.0407(外围信息提取变量),可见,外围信息提取变量的影响最大,时滞变量的影响次之,也不能被忽视,而补充信息提取变量的影响较小,在一些情况可以被忽略.再看最大值,同样也都提供正向识别信息,5个数据集的平均影响程度从大到小的顺序是外围信息提取变量(0.0887)、时滞变量(0.0608)和补充信息提取变量(0.0356).关于最小值,5个数据集的平均影响程度都小于0,都提供负向识别信息,会降低识别准确率,降低的幅度由小到大的顺序是外围信息提取变量(-0.0061)、时滞变量(-0.0174)和补充信息提取变量(-0.0174),最后可以得出结论:外围信息提取变量的正向影响最大,负向影响最小;补充信息提取变量的正向影响最小,负向影响最大;时滞变量介于二者之间. 通过影响程度计算验证了补充信息提取变量、时滞变量和外围信息提取变量均能够弥补由弱因果关系的缺失所导致的传递信息丢失,尤其是外围变量组的信息提取变量,平均提升程度达到了4%,而且实现了困难的降维. 本文只关注不同的影响因素之间的敏感性比较,因此只需要计算一个固定的扰动数据比率即可,取δ=0.1.也是使用影响程度计算中的5个数据集,但选择5个数据集的综合指标,5个综合指标分别是:工业增加值同比增长率、房地产投资累计增长率、固定资产投资累计增长率、社会消费品零售总额同比增长率和居民消费价格指数(上年同月),从核心因素和外围因素两个方面进行对5个综合指标的敏感性计算,具体情况如图6所示. 1)核心与外围因素的敏感性 图6 敏感性计算Fig.6 Sensitivity calculation 本文仍然使用后验分布抽样识别准确率进行变量之间的敏感性计算,为计算一个综合指标(5个综合指标中之一)对其它指标(核心指标或外围指标)的敏感性,首先计算没有扰动的后验分布抽样识别准确率,然后计算以比率δ扰动后的后验分布抽样识别准确率,再取两个识别准确率的差的绝对值,将其作为敏感性计算的结果(敏感程度),具体的计算方法见公式(6).无论是核心变量还是外围变量(外围信息提取变量)均采用统一的方法进行敏感性计算,具体情况如图6所示,其中横轴表示影响因素(变量)的编号,纵轴表示敏感程度.在外围变量的敏感性计算中,可以不考虑综合指标所在变量组的信息提取变量的敏感性.对于没有综合指标变量组中的变量,可以采用类似的方法进行敏感性计算. 2)敏感性统计表 对生成图6的数据进行简单的统计运算可得到表4.从图6和表4中我们能够发现,大多数综合指标对核心因素与外围因素的敏感性变化相对较小,只有一个综合指标-房地产投资累计增长率,对编号为17,18,19,20,21,22,23,24变量组的信息提取变量非常敏感,敏感性程度依次是0.1342、0.1256、0.0866、0.1039、0.1083、0.1169、0.1385和0.1255.通过敏感性计算可以发现敏感与不敏感的因素,有利于揭示深层次的经济规律,加深对宏观经济的认识,并为宏观经济决策提供支持. 表4 敏感性统计表Table 4 Statistical table of sensitivity 本文仍然选择影响程度计算中的5个数据集和相应的因果关系网络,使用公式(7)和公式(8)进行汇聚与扩散影响计算. 1)汇聚影响 汇聚影响是所有父结点对一个共同的子结点的影响,是诸多影响中的最主要和最大的影响.在汇聚影响计算中,本文只选择有父结点的变量进行汇聚影响计算,5个数据集的汇聚影响计算的具体情况如图7所示,横轴是被影响因素(子结点)的编号,纵轴是父结点对子结点的影响程度. 图7 汇聚影响Fig.7 Convergence effect 工业增加值:平均汇聚影响是0.0584,最大汇聚影响是0.1697,最小汇聚影响是0.0031;房地产投资额:平均汇聚影响是0.1418,最大汇聚影响是0.4156,最小汇聚影响是0.0087;固定资产投资额:平均汇聚影响是0.0511,最大汇聚影响是0.1265,最小汇聚影响是0.0039;社会消费品零售总额:平均汇聚影响是0.2589,最大汇聚影响是0.4239,最小汇聚影响是0.0824;居民消费价格指数:平均汇聚影响是0.0556,最大汇聚影响是0.1656,最小汇聚影响是0.0032. 2)扩散影响 扩散影响是一个父结点对它的所有子结点的影响,同样,在扩散影响计算中,本文也只选择有子结点的变量进行扩散影响计算,每一个数据集只选择两个变量,用它们排序后的编号表示变量,并分别给出它们对子结点影响的平均值、最大值和最小值,5个数据集的具体情况如表5所示. 在核心变量中的汇聚与扩散影响是对一个变量的各种影响因素中至关重要的两种,而且不具有可替代性.在时间序列变量之间基于抽样识别准确率的影响程度计算、敏感性计算和汇聚与扩散影响计算将为宏观经济指标的量化分析提供有效实用的方法,并与计量经济和统计方法形成互补. 当数据中所蕴含的信息不充分时,无法可靠地基于数据建立因果关系网络,会有一些因果关系丢失,从而降低在因果关系网络中信息传递的有效性和可靠性.本文结合变量排序和局部贪婪搜索-打分进行因果关系网络结构学习,最大限度地降低了对时间序列数据量的需求,并提高了学习的效率和可靠性;为弥补因果关系缺失而导致的信息传递不完整性,在给出信息提取变量和学习方法的基础上,通过建立信息提取变量来实现基于后验分布的时间序列变量组的信息压缩提取,再结合时间序列变量的核心组与外围组划分,以及外围变量的分组,实现了对高维时间序列数据的降维,并提高了信息传递的完整性;使用宏观经济时间序列数据,验证了变量之间的影响程度计算、敏感性计算和汇聚与扩散影响计算方法的实用性和有效性. 表5 扩散影响统计表Table 5 Statistical table of diffusion impact 进一步的工作是将因果关系网络学习、信息提取变量构建和信息传递计算等向金融纵向大时间序列进行拓展.
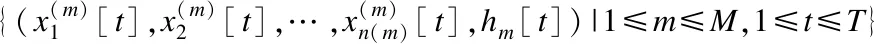
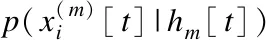
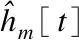
3 时间序列变量之间的信息传递计算
3.1 影响因素的局部结构
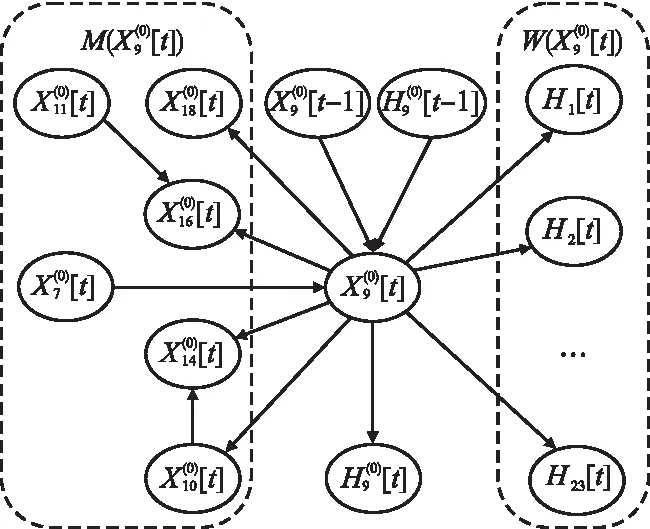
3.2 基于后验分布抽样识别准确率的信息传递计算
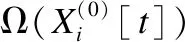
3.3 基于信息传递的时间序列变量之间影响计算
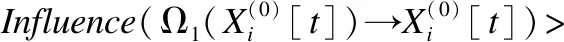
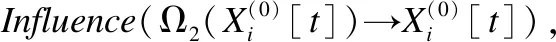
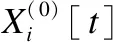
4 实验与分析
4.1 时间序列数据集
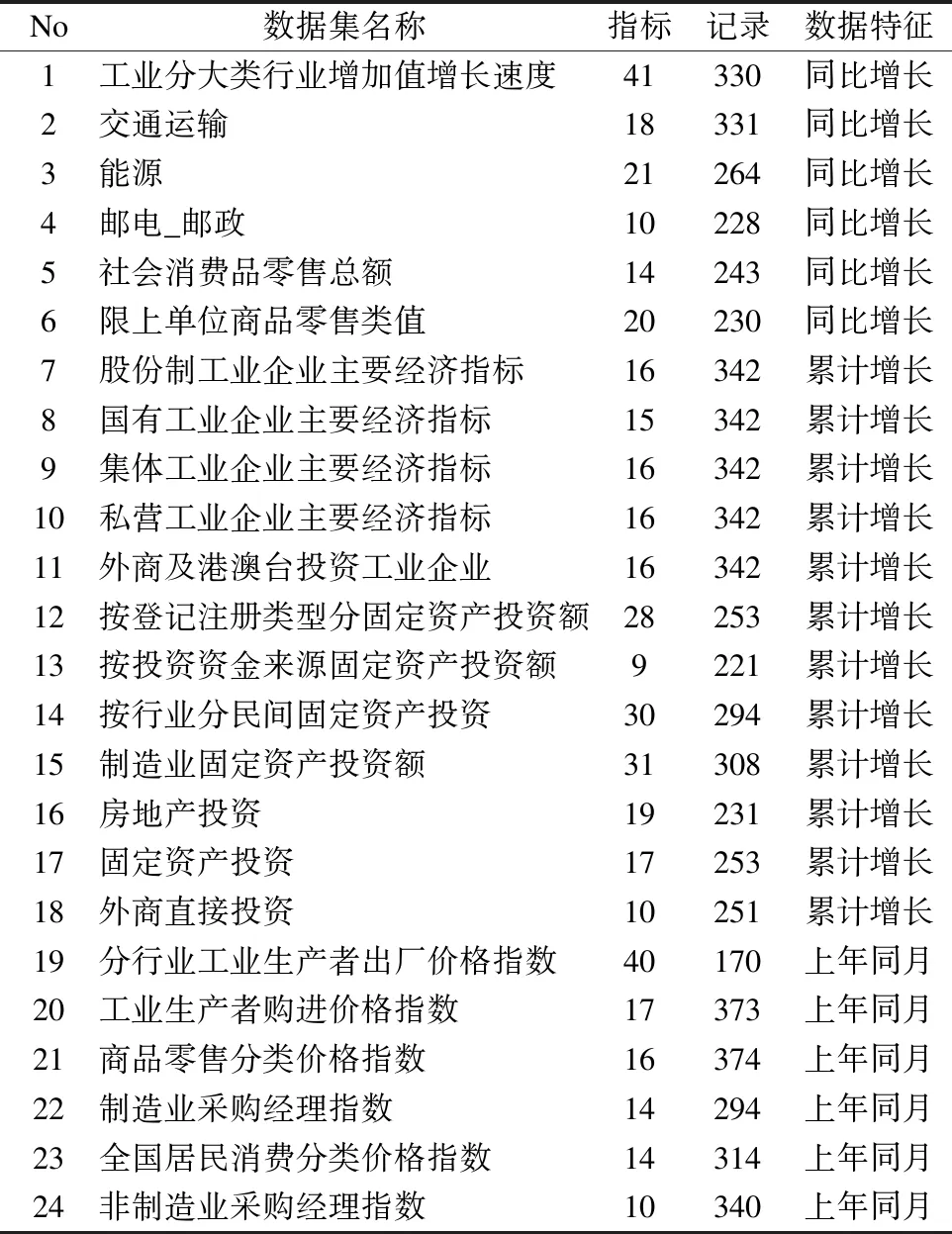
4.2 因果关系网络结构学习

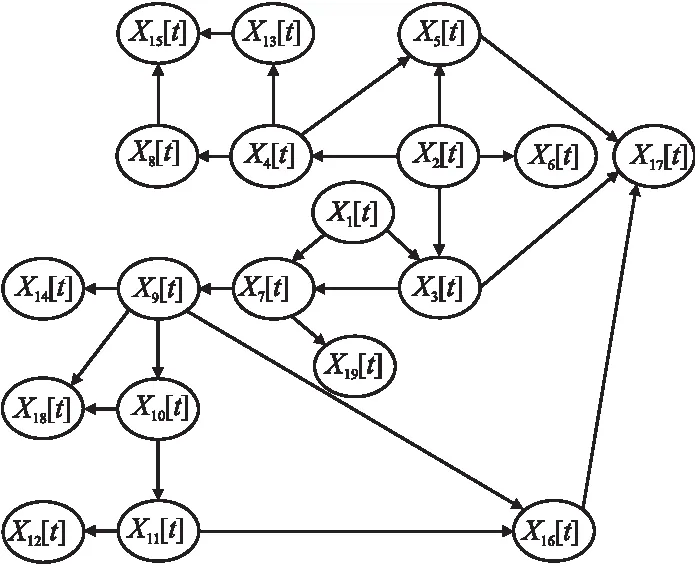
4.3 信息提取变量的迭代收敛性

4.4 时间序列变量之间的影响程度计算
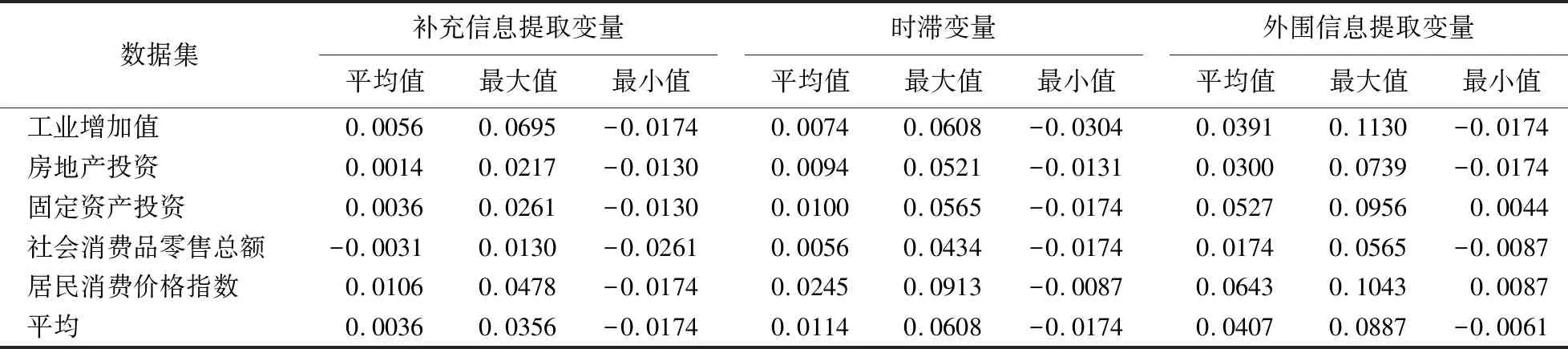
4.5 时间序列变量之间的敏感性计算
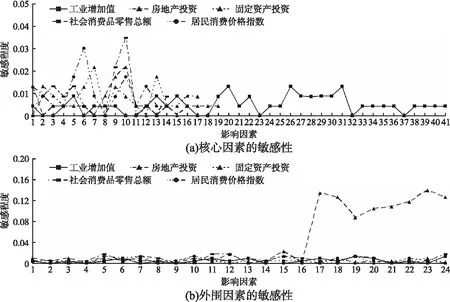
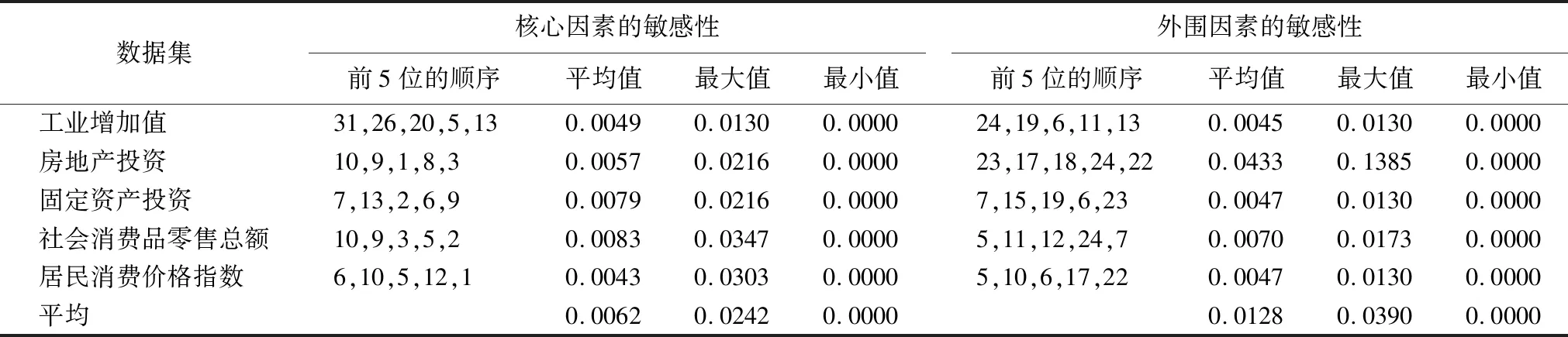
4.6 汇聚与扩散影响分析
5 结论和进一步的工作