求解高维优化问题的新型平衡优化器算法
2023-05-12申元霞汪小燕张学锋
申元霞,汪小燕,张学锋
(安徽工业大学 计算机科学与技术学院,安徽 马鞍山 243000)
1 引 言
目前,随机优化算法已经成功应用于工程优化问题,如模式识别[1]、PID控制器[2]等.从算法的设计思路上可以将随机优化算法划分4类,第1类是受生物进化启发提出的进化优化模型,如差分进化算法[3]等.第2类模拟群居动物的行为而实现群智能优化模型,如粒子群优化算法[4]、灰狼优化算法[5]等.第3类算法设计灵感来源于人类的社会行为,如教与学优化算法[6]、帝国竞争优化算法[7]等.第4类算法是模拟物理现象和规则设计的优化模型,如重力搜索算法[8]、量子优化算法[9]等.虽然各个优化模型的设计思路不同,但是共同的目标都是通过最短的搜索时间,寻找到待求解问题的全局最优解.
平衡优化器EO (Equilibrium Optimizer)[10]是2020年提出的一种新的随机搜索优化算法,算法的提出是受控制容积动态质量平衡的物理现象启发.目前EO算法已有效解决二极管参数估计[11]、光伏参数估计[12]、图像分割[13]、0-1背包[14]等工程优化问题.
虽然EO算法在低维问题上展现良好的优化性能,但是在求解高维问题上,EO算法进化中后期会出现停滞现象.为了改善EO算法求解高维复杂问题的优化性能,本文首先分析EO寻优过程中陷入进化停滞原因,接着提出了新型EO算法,新算法通过设计动态更新的生存概率来增强群体的探测能力;为了避免平衡池候选解同质化,对候选解实施依概率自我学习;同时将种群分为两组,一组采用改进EO策略学习,另一组采用提出的混合反向学习机制,异构学习模式可以避免群体陷入进化停滞.对比实验结果表明改进的EO算法在高维优化问题上表现了良好的寻优性能.
2 平衡优化器(EO)
EO是通过质量平衡方程中质量在一个控制容积内进入、产生和离开的过程来模拟寻优的过程.在EO中,将待求解问题的解看作控制容积内浓度,寻优的过程是受控容积内浓度达到平衡状态的过程.
假设Ci(t)是第i个个体第t时刻浓度向量,t+1时刻个体浓度的更新方程为:
(1)
式中i∈(1,…,N),N为种群规模.Ceq为平衡池中随机选择的一个候选解.V为单位值,取常值为1[10].
平衡池是为寻优过程中提供候选解的集合,候选解是每次迭代后种群按个体适应度排列,由排列前4位个体及其平均值组成.
(2)

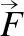
(3)

β=(1-t/T)a2t/T
(4)
(5)
式中r2和r3为服从[0,1]之间的随机数;GP为生成概率,GP取值越小越利于个体的探索;越大则利于个体的局部学习,文献[10]取值为0.5.
3 EO寻优行为分析
EO的寻优方式不再是个体向最优解逐渐逼近,而是从平衡池中随机选择一个候选解,以该候选解为中心,实施邻域搜索,搜索半径是由更新方程中的运动项控制.为了便于分析,将EO模型简化一维模型进行讨论,将式(5)代入式(1)可得式(6):
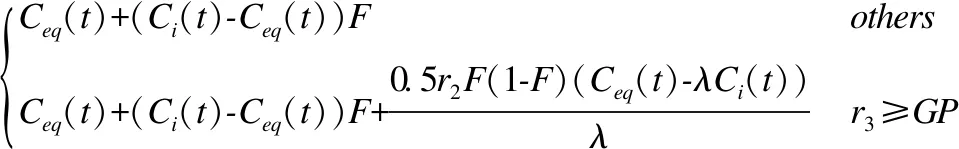
(6)
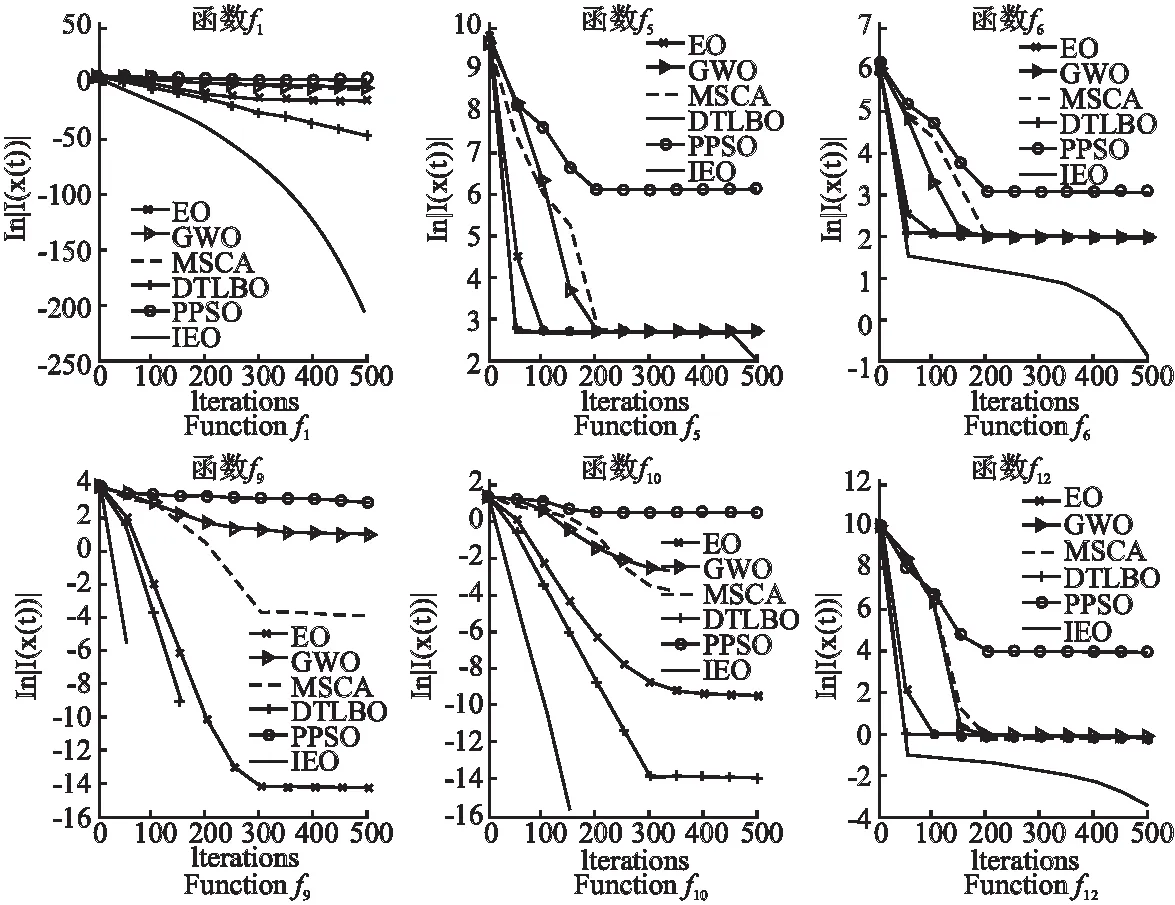
由式(6)可知当r3 图1 F随迭代次数的取值变化图Fig.1 Variation of F over course of iterations 当r3≥GP时,新个体的生成半径是更新方程的第2项和第3项之和.第3项为0.5(r2/λ)F(1-F)(Ceq(t)-λCi(t)).令Ф=0.5F(1-F),由于F的取值范围在[-1.264,1.264],所以Ф取值范围在[-1.43,0.125].令Z=r2/λ,r2和λ均为独立的[0,1]随机变量,可计算Z的概率分布为式(7): (7) 由式(7)可得,z取值在(0,1]之间的概率为0.5;当z值大于1的概率随着z值的增加而指数递减.第3项可表示为ФZ(Ceq(t)-λCi(t)),由Z的概率分布可知,Z有50%取值概率可以压缩Ф(Ceq(t)-λCi(t))的值,50%取值概率可以扩大Ф(Ceq(t)-λCi(t))的值.当r3≥GP时,在第2项和第3项共同作用下群体偏向探索.但当群体聚集,Ci(t)等同与Ceq(t)时,第2项(Ci(t)-Ceq(t))F为零,而第3项为ФZ(1-λ)Ceq(t),仍具有个体更新的能力,但是由于Z和λ取值的限制,个体探索能力减弱. 标准的EO里生成概率取值为0.5.通过EO寻优行为的分析可知,当r3 固定的生成概率限制了群体的探索能力.为了提高群体在进化中后期的探测能力,提出了自适应的生成概率,定义见式(8): GP(t)=g0-g1(1+t/T) (8) 由式(8)可知生成概率随着迭代次数的增加从g0-g1而递减g0- 2g1,该策略让群体随着迭代次数的增加有更多机会进行探索. EO学习策略是对平衡池中的候选解进行利用和探索,候选解的质量直接影响寻优的效果.如果平衡池排名前4位的候选解产生聚集的情况,即使平衡池中有当前种群的均值候选解,但是由于均值候选解被选中的概率只有0.2;因此这种情况易使整个群体陷入局部最优.候选解的自我学习可以帮助逃离当前的局部最优.本文采用文献[15]提出的学习策略,定义见式(9): (9) 式(9)中L为学习步长,r4为[0,1]分布的随机变量.当Ceq从平衡池被选择后,Ceq有50%的概率按式(9)学习. 虽然自适应的生成概率增加了群体实施探索的机会,但是指数项F随着迭代次数的增加将逐渐减小,这将使整个群体在进化中后期探索能力不足.为了进一步增强群体探索能力,本文提出混合反向学习策略,并对群体实施异构学习模式.将种群分为两个组,一个组采用改进的EO学习策略,称为E组;另一个组实施混合反向学习策略,称为H组. (10) 式中的Xmax和Xmin分别是待求问题的上限和下限;r5为[0,1]分布的随机变量.新的个体是由E组的个体Ci和其反向学习个体加权得到,混合反向学习策略比单纯的反向学习策略可以增加获得优秀个体的可能. IEO伪代码如算法所示. 算法.IEO 输入:种群最大迭代数T;E组和M组种群规模分别为n和N-n; 输出:种群最优解gbest; 1.初始化E组种群C和H组种群X; 2.计算H组个体X的适应度,将最优适应度值赋给Xgbest. 3.whilet<=Tdo 4.按式(8)计算GP(t); 5.fori←1 tondo 6.计算适应度值f(C);按式(2)构建平衡池ES; 9.end if 10.Ceq←随机选择平衡池ES优秀个体; 11.if rand<0.5 12.Ceq按式(9)自我学习; 13.end if 14.按式(1)、式(3)、式(4)、式(5)计算C(i); 15.end for 16.fori←1 toN-ndo 17.按式(10)计算X(i); 18.ifX(i)适应度值优于Xgbestthen 19.Xgbest←X(i) 20.end if 21.end for 23.end while 为了检测本文算法的优化能力,新算法(IEO)与标准EO、向量PSO算法(PPSO)[4]、 灰狼算法(GWO)[5]、动态TLBO算法(DTLBO)[6]、基于记忆导向的SCA算法(MSCA)[16]进行比较. 表1 函数的定义Table 1 Define of benchmark test functions 采用文献[10]给出的13个测试函数,包括单调测试函数和多模测试函数,测试函数定义如表1所示.在对比实验中,采用种群规模均为30,其中IEO中的E组和H组规模分别为20和10;最大迭代次数T=500,独立运行次数为25次,维数D为200和500. 参数设置:标准EO中GP=0.5,a1=2,a2=1;IEO中g0=0.8,g1=0.3,L=2(参照文献[15]推荐值);MSCA中a(t):2→0,按文献[16]设置不同引导个体数Δt;GWO中a:2→0;DTLBO中Jr=0.3,w=10;tf∈(0,2).每种算法运行后记录其平均适应度值及其标准差,并用Wilcoxon秩和检验(显著性水平α=0.05)来评价IEO与其他算法之间性能差异. 表2和表3分别给出了200维和500维条件下6种算法独立运行25次后获得平均适应度及其标准差.对于每个函数用加粗字体来表示获取的最优结果. 由表2和表3可知,除函数f8外,IEO在12个函数上200维和500变量的条件下寻优结果要远优于EO、GWO、MSCA、DTLBO和PPSO算法.对于函数f8,IEO寻优结果要劣于MSCA、DTLBO和PPSO,优于EO和GWO.IEO已找到200维和500维f9,f10和f11这3个多模函数的理论最优值.IEO不仅获得了较高精度的平均值,也获得了低方差,说明算法也具有较好的稳定性.用Wilcoxon秩和检测的评价结果,可获得6个算法平均排名,结果显示在表2和表3的“rank”栏.从表中可知在200维和500维变量的条件下,IEO综合排名均为第1. DTLBO在f1~f7、f10、f11和f12函数上优化结果优于EO、GWO、MSCA和PPSO.在200维变量的条件下,DTLBO与IEO寻优结果相同,找到了函数f9和f11的理论最优解;在500维变量的条件下,DTLBO找到了函数f9的理论最优解;DTLBO综合排名均为第2,这表明DTLBO在高维优化问题上也展现了良好的优化性能.但是在求解精度上,与IEO还存在差距,如对于200维变量的条件下函数f3,DTLBO优化结果精度为103,而IEO优化结果精度为10-170;对于函数f6,DTLBO优化结果精度为101,而IEO优化结果精度为10-2. 表2 各个算法在函数变量为200维的实验结果Table 2 Optimization results of each algorithm on 13 test functions of 200 dimensions 表3 各个算法在函数变量为500维的实验结果Table 3 Optimization results of each algorithm on 13 test functions of 500 dimensions 对于函数f8,与其他5种算法相比,PPSO获得最优解.但是PPSO在其他12个函数上优化结果均要劣于其他算法.收敛曲线分析可以直观地观察算法陷入停滞现象和收敛速度.图2给出了6种算法在D=500时的收敛曲线.由图2可以看出,IEO的收敛速度快,在给定代数下的收敛精度也达到最高. 从f9和f10收敛曲线图可以看出,IEO可以快速寻找到理论最优值.从f5、f6和f12收敛曲线图可以看出,IEO具有良好的寻优能力,不仅没有在进化的中后期陷入进化停滞,而且在进化后期仍具有强的搜索能力,不断提高解的精度.特别对于f5,IEO在进化过程中,也进入局部收敛,但是在进化后期可以逃逸局部极值继续寻优.除了f1,EO在其他5个函数进化过程的中后期均陷入进化停滞,也无法逃离局部极值.DTLBO的收敛速度优于EO、GWO、MSCA和PPSO,但是在f5、f6、f10和f12的进化过程中也陷入了局部收敛. 由上述分析可知,IEO具有高的收敛精度和快的收敛速度,而且受维度变化影响小,求解高维优化问题具有良好稳定性.这主要是因为IEO自适应生成概率使得算法在进化初期局部利用和全局探索的概率相当,群体可以快速地学习平衡池的优秀候选解,从而获得好的收敛速度.随着迭代次数的增加,由于E组学习模式中指数项的递减,群体逐渐进入聚集;但是平衡池优秀解的自我学习和H组的混合反向学习可以帮助从局部极值中跳出.综上所述,在高维条件下IEO在求解精度、收敛速度和稳定性方面都展现较好的进化寻优性能. 图2 6种算法在6个函数上的收敛曲线Fig.2 Convergence performance of the six algorithms on the 6 test functions 本文针对标准平衡优化器易出现进化停滞的问题进行了分析.通过分析得出,标准平衡优化器固定的进化概率、平衡池中候选解的集聚和中后期指数项的递减都可能导致进化停滞.基于标准平衡优化器的寻优分析,提出改进的平衡优化器(IEO).首先设计了自适应调整的生成概率,在平衡算法的利用与探索的同时,提高算法在中后期的探索能力以防止算法陷入停滞.接着对平衡池的候选解进行自我学习,不仅可以有效提高群体的收敛速度索,同时可以避免候选解的集聚.最后通过异构双组的学习模式,让辅助群组在中后期提供探索动力.实验结果表明 IEO在求解高维函数优化问题具有一定优势,可以达到较好的收敛速度和收敛精度.接下来的研究方向是将本文算法扩展到高维多目标问题求解上.
4 改进的EO(IEO)
4.1 自适应的生成概率
4.2 优秀解的学习策略
4.3 种群的异构学习模式
4.4 IEO算法流程
5 数值仿真实验及结果分析
5.1 测试函数
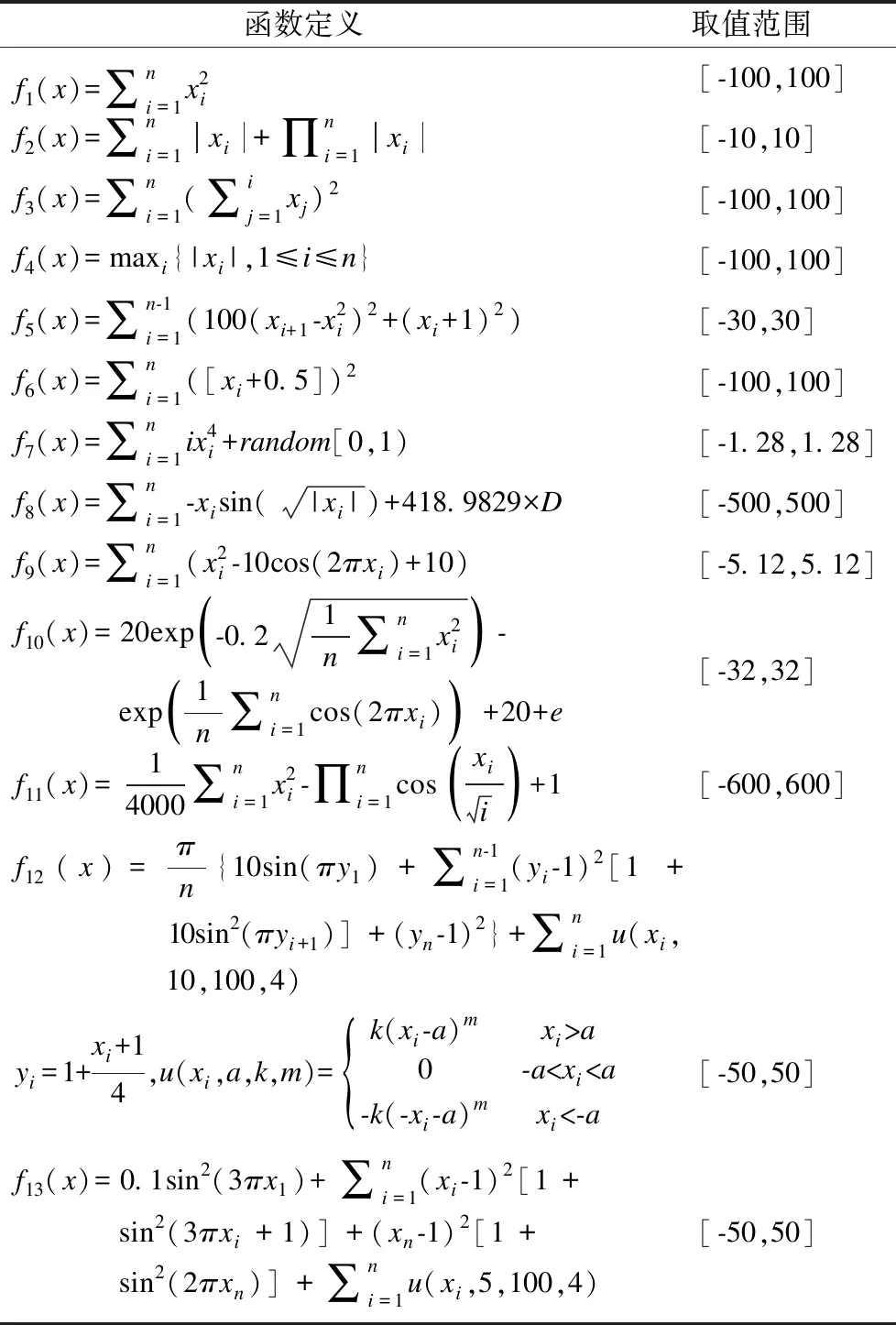
5.2 实验结果分析


6 结束语
