沥青面层混合料松弛模量的跨尺度拟合分析
2023-05-12贾大伟杨荣琦魏哲文
付 军 贾大伟 杨荣琦 孙 毅 魏哲文 龚 锋
(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (潜江市公路事业发展中心2) 潜江 433100)
0 引 言
松弛模量是沥青路面黏弹性分析的重要参数[1-2],广义Maxwell模型和Prony级数参数适用于松弛模量的定量数值表征[3-5].目前利用沥青混合料松弛试验获取松弛曲线然后拟合得到Prony级数参数最为常见[6-7],直接试验数据可信度较高,但对仪器和应变控制要求高,试验数据离散性导致误差[8],而且耗费大量人力、物力和时间.因此如能在相关试验的基础上,结合数值模拟方法分析及预测松弛模量不失为一种可选思路.
沥青混合料是一种广义多相复合材料,宏观尺度上可视为连续均匀介质,但难以完美解释沥青混合料多相介质和细观结构特性的影响.而从细观尺度角度分析,沥青混合料是由骨料、沥青砂浆、界面和空隙组成的非均质四相复合材料[9],其中最主要的两相介质为沥青砂浆与骨料.沥青砂浆相均质性较好,可以通过松弛试验得到较为精准的数据,骨料的物理力学性质也相对明确.基于均质化分析方法,结合细观本构关系和变量模拟分析,可以实现沥青混合料宏观松弛力学表征参数的预测,提高沥青混合料的松弛模量分析效率.国内外学者针对沥青材料及路面的多尺度分析方面开展了前期研究.董泽蛟等[10-11]基于数字图像识别技术,进行了细观尺度下的沥青混合料二维有限元分析,结果表明忽视细观结构的影响会导致沥青混合料设计性能与实际性能之间存在差异.曹鹏[12]利用有限元子模型方法,将沥青混凝土材料简化为沥青胶结料和集料两相介质,进行了多极化分析.Kim等[13-14]以沥青路面结构为研究对象,建立了双向耦合的多尺度有限元模型,考虑沥青混凝土黏弹性、非连续均匀和各向异性特性,预测沥青混合料的永久变形与破坏,结果表明该模型能大大减少总体刚度阵规模,减少计算时长,提高计算精度.Allen等[15-16]以柔性沥青路面为应用对象,模拟分析细部子模型的微尺度响应(包括材料各相异性和微裂纹),考虑松弛模量的多尺度传递,模拟分析并预测沥青路面的宏观裂纹和永久变形.
文中在沥青胶浆松弛模量试验分析及拟合的基础上,应用参数化建模和随机投放算法模拟沥青混合料内部复杂细观几何特征,结合细观-宏观跨尺度关联机理,预测宏观尺度沥青层混合料松弛模量并应用于沥青路面性能响应分析.
1 黏弹性本构关系
1.1 广义Maxwell模型
沥青混合料每一个松弛时间都可以与表示材料响应的力学模拟中的黏性元素相关联.为了合理地描述沥青混合料的黏弹性特性,将多个Maxwell单元与单个弹簧单元并联构造,以创建一个广义的Maxwell模型,松弛模量为
(1)
式中:E∞为广义Maxwell模型中并联单个弹簧单元的弹性模量,即长期松弛模量;Ei为第i个Maxwell子模型中弹簧的弹性模量;τi为第i个Maxwell子模型的松弛时间,且
τi=ηi/Ei
(2)
式中:ηi为第i个Maxwell子模型黏壶的黏度.相比单个的Maxwell模型,广义Maxwell模型可更真实地描述沥青混合料黏弹性力学行为,其总应力为各元件应力之和,即
(3)
式中:σi为第i个元件的应力;σ为各元件应力之和;N为元件个数.
1.2 Prony级数参数拟合
Prony级数的各项参数E∞,Ei,τi(式1)可以很好地描述广义Maxwell模型.但需要对模拟松弛曲线进行拟合.首先选定一个在对数坐标上均匀分布的正数序列[τ]n,此时数据拟合问题成为Prony级数中的待定系数Ei(Ei>0)的确定,使得Prony级数函数值E(t)与试验数据tn时间下的松弛模量E(tn)之间的距离最小.
(4)
上述问题转化为求解线性规划问题.
MINIMIZE|BC-A|.其中:C>0
(5)
设置一系列松弛分析步,每个分析步的时间为对数坐标上均匀分布的时间.沥青砂浆模型选取松弛分析步分别等于2.7×10i,其中i=-1,0,1,2,3.其中,长期松弛模量E∞可以通过曲线上的残余应力σ∞直接计算得到,由模拟松弛试验计算结果可计算得出E∞,即:
E∞=σ∞/ε0
(6)
通过Matlab求解线性规划问题,调用MATLAB线性规划求解函数C=LSQNONNEG(B,A)进行线性规划求解向量矩阵C,即Ei.
2 模拟松弛试验
2.1 沥青砂浆模拟松弛试验
假设沥青砂浆为均质黏弹性材料,其黏弹性本构模型采用5单元广义Prony级数模型.应力松弛试验的有限元模型尺寸为100 mm×300 mm[17],单元类型为CPE3,模拟沥青砂浆试件被均匀拉伸的过程见图1.
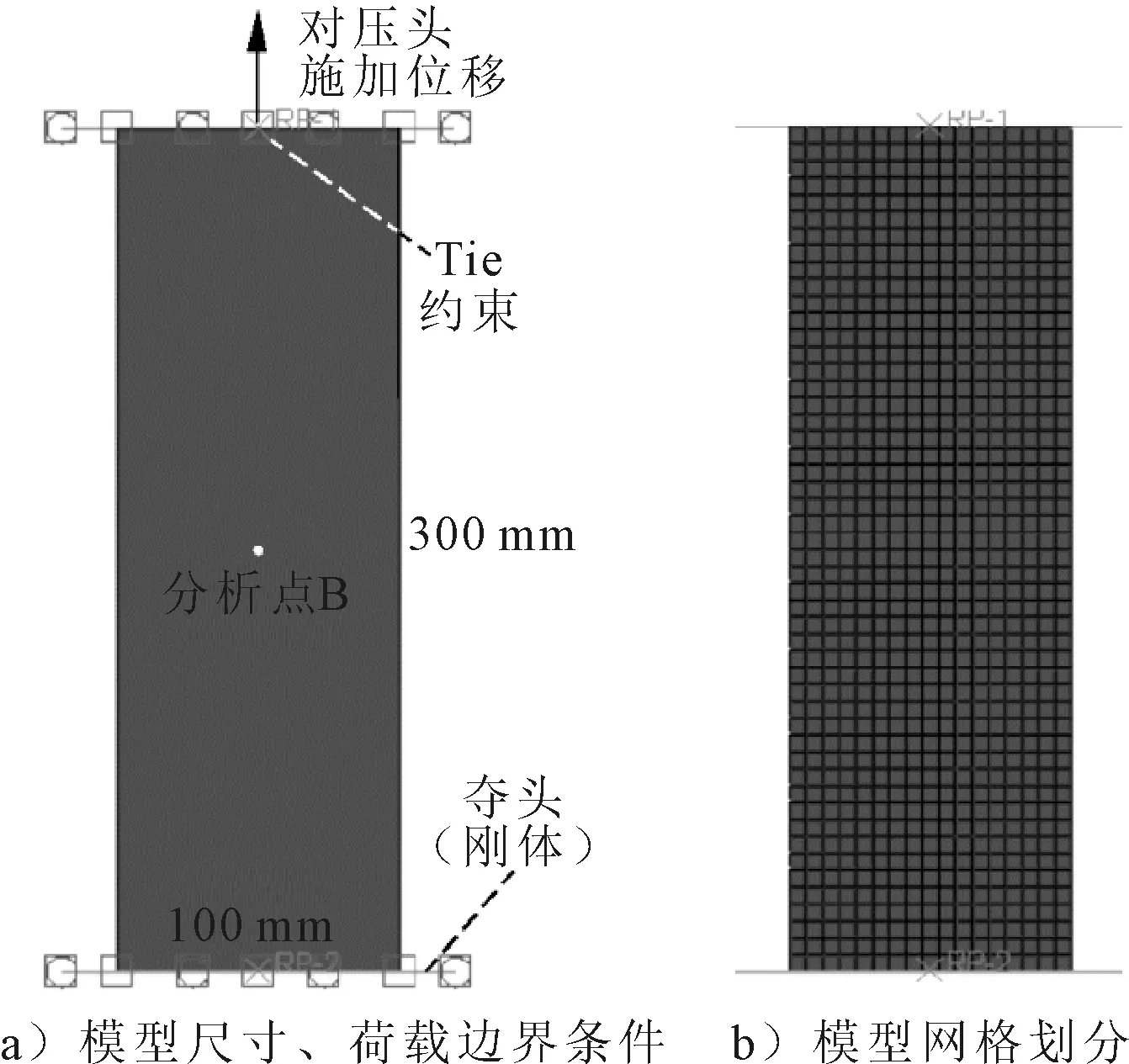
图1 沥青砂浆应力松弛试验模拟
定义沥青砂浆的瞬时弹性与黏弹性两种材料性能,参数采用室内真实松弛试验结果,沥青砂浆Prony级数参数见表1.采用时域分析方法,考虑到泊松比随时间变化比较小,假定μ(t)取为常数0.3.

表1 试验用沥青砂浆Prony级数参数
2.2 模拟结果分析
选取试件中心点B作为特殊分析点,B点位置见图1.松弛模量由分析点的应力除以初始恒定应变ε0为
E(t)=σ(t)/ε0
(7)
真实松弛模量与模拟分析对比见图2a),不同时刻的松弛模量模拟值与真实值基本吻合.图2b)为分析区域各平均应力分量随时间变化图,Mise应力与竖直方向应力S22基本相等.随着松弛时间的增加,Mise应力与S22值逐渐减小,有着明显的应力松弛现象,与松弛试验真实情况相符.5单元Prony级数模型预测松弛曲线与真实试验结果非常接近,误差小于1.2%(见图3),说明5单元广义Prony级数模型精度较高,应力松弛试验数值模拟分析在一定程度上可以较准确地预测其松弛模量.

图2 模拟松弛模量与真实试验结果对比及B点各应力分量随时间变化图
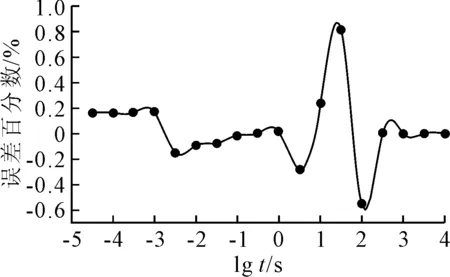
图3 拟合松弛曲线与真实试验误差百分比
3 面层沥青混合料跨尺度松弛模量预测
3.1 细观-宏观跨尺度关联机理
细观尺度的沥青混合料是由骨料、沥青砂浆、界面和空隙组成的非均质四相复合材料.可以通过均质化方法,结合细观尺度本构关系和细观变量表达式,得到宏观尺度力学响应以描述宏观整体特征,非均匀材料的均匀化过程见图4.其中细观单元称为代表性体积单元(RVE),应具备以下特征:①多相复合材料等效力学是相对连续的;②复合材料整体可由RVE叠加形成.

图4 非均匀材料的均匀化过程
沥青混合料细观尺度均匀化过程,包括:①描述多相复合材料细观几何参数及材料参数,包括各组分(沥青砂浆、骨料、界面和空隙)材料参数、几何形状、体积占比等;②求解RVE在均匀边界荷载作用下各组分内的局部应力与应变;③将细观RVE应力应变响应进行均质化处理,用统计上平均意义等效的均质材料单元代替多相复合材料单元.
将非均匀介质局部区域的力学响应进行均质化处理.
(8)

将细观模型的边界条件假定为均匀的,则由细观模型的应力场,宏观模型均匀化的应力场为
(9)

细观尺度的应变场同样地可表示出宏观尺度的均匀化应变场.
(10)
(11)
(12)
3.2 松弛模量预测
为描述沥青面层混合料细观复杂几何特征,模拟粗骨料与孔隙的随机分布,使用PFC2D软件实现粗骨料与孔隙的随机投放过程.定义预设区域设置为100 mm×300 mm,粗骨料的粒径及体积占比符合《公路沥青路面设计规范》规定,粒径取18~24 mm,体积占比取46%.孔隙等效直径与孔隙率参照文献[15],生成模拟松弛试验随机投放模型见图5a).基于随机投放几何模型建立沥青混合料松弛试验有限元模型,见图5b).

图5 模拟松弛试验随机投放模型及沥青混合料松弛试验模型
黏结料-骨料界面厚度根据文献[15]设置为0.1 mm,各相材料参数如表2.沥青砂浆的松弛模量Prony级数参数见表1.

表2 细观尺度各相材料参数
结合沥青砂浆的松弛试验模型模拟结果,实现了沥青混合料松弛模量预测(见图6).取模拟试件中心区域RVE为分析区域进行分析,得到松弛模量曲线见图7,拟合得到沥青混合料的Prony级数参数见表3,结果表明:松弛参数变化规律合理可靠.

表3 沥青混合料Prony级数拟合参数
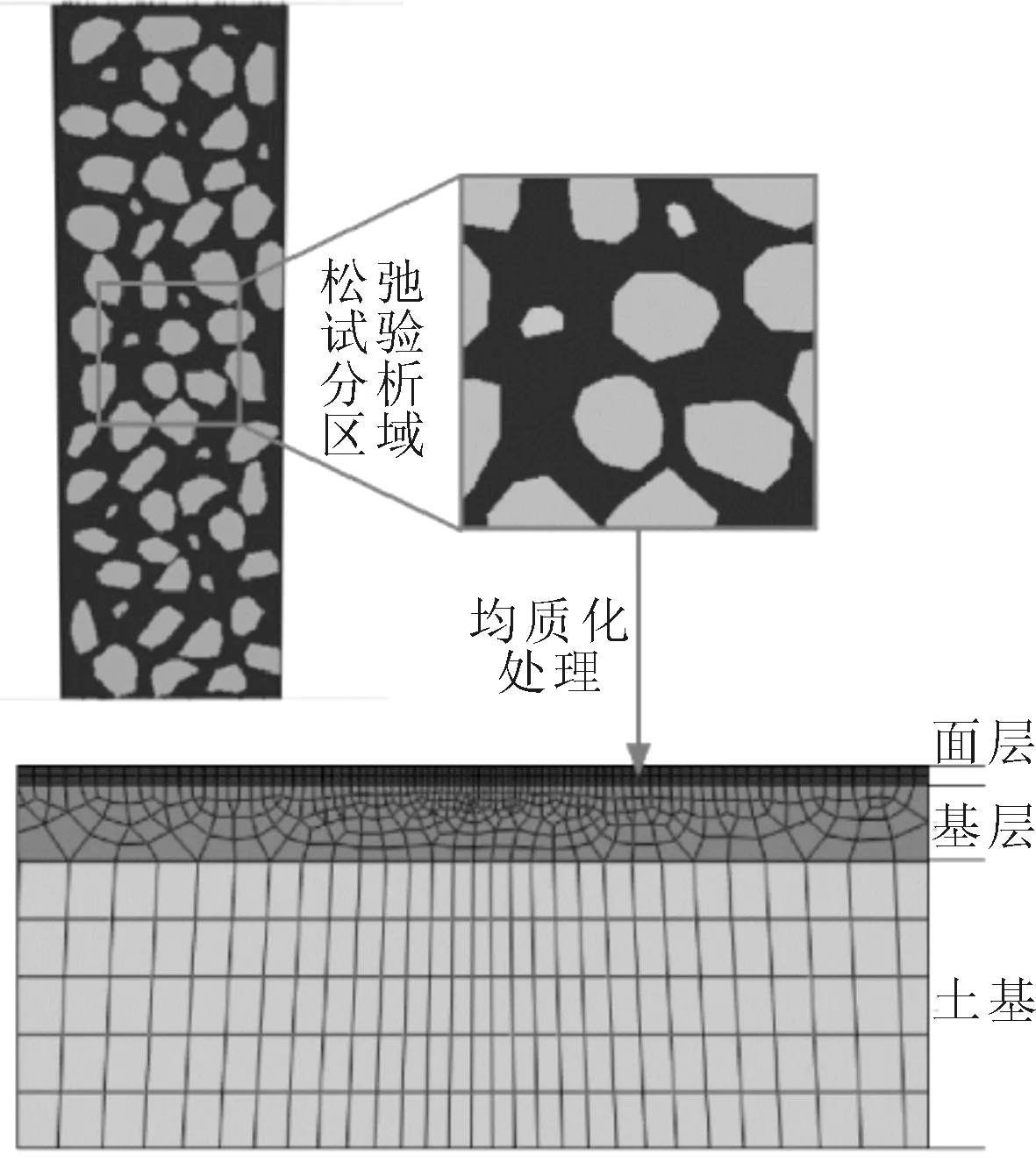
图6 跨尺度松弛模量关联与预测
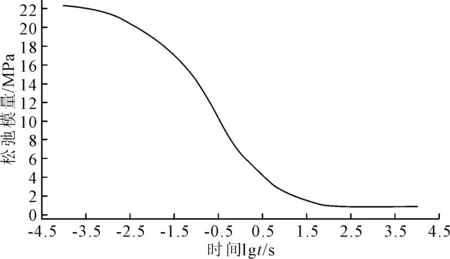
图7 沥青混合料松弛模量预测曲线
4 沥青路面(面层)黏弹性响应分析
选取两种典型沥青路面结构(见表4),考虑其沥青面层黏弹性影响下的应力状态(见图8),其中面层沥青混合料黏弹性参数如表3,行车荷载加载模式见图9.
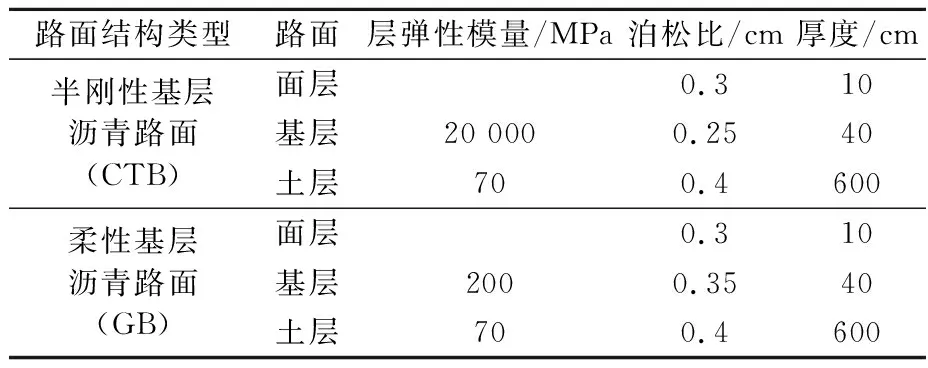
表4 沥青路面宏观模型路面结构层参数
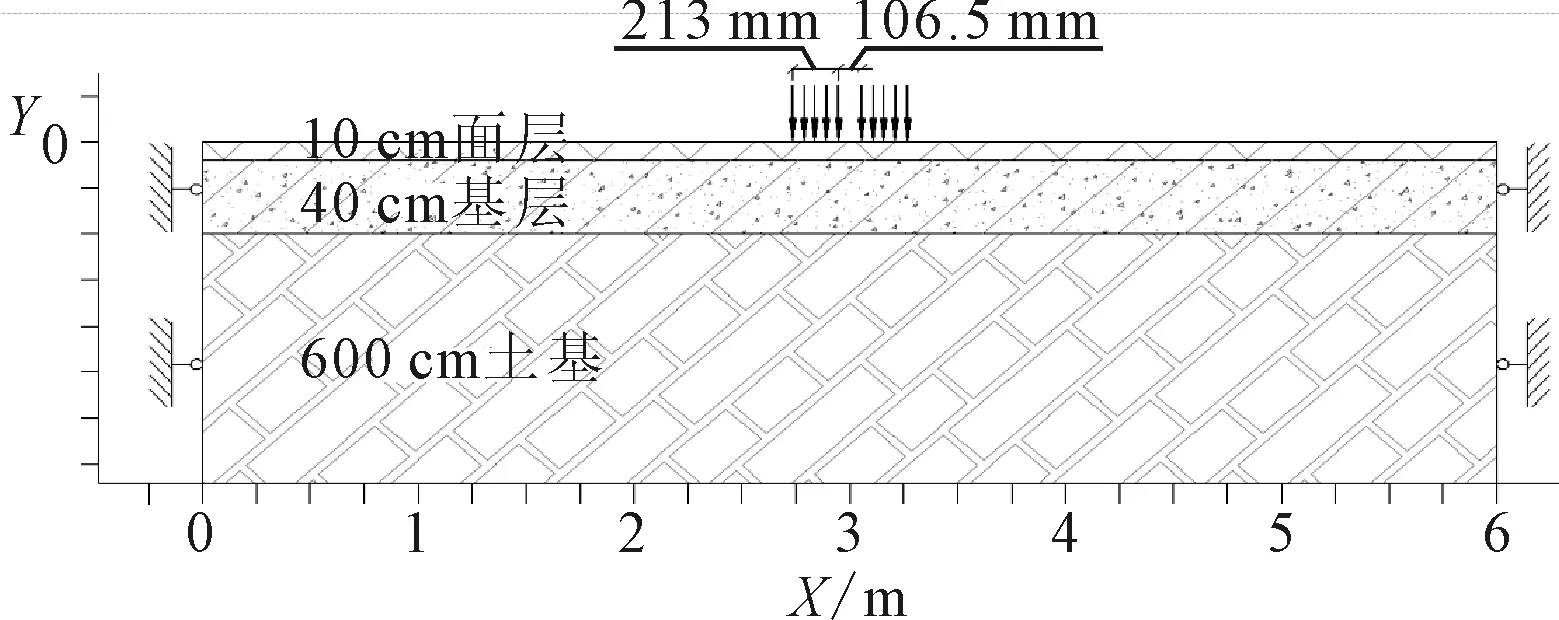
图8 沥青面层黏弹性应力响应态分析
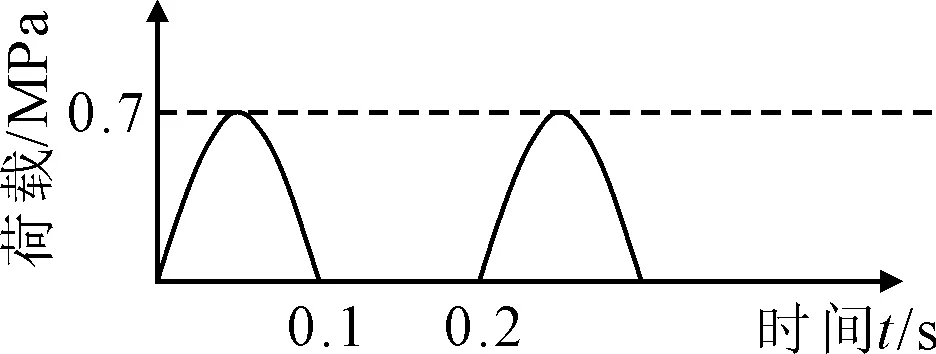
图9 行车荷载加载模式图
图10为半正弦荷载(单次)横向应力黏弹性响应.由图10可知:单次车载荷载循环结束时刻(0.2 s),CTB与GB面层中均存在未完成消减的残余应力.经过多次标准轴载循环作用,路面结构层中来不及消减的残余应力形成了累积残余应力.CTB路面与GB路面累积残余应力见图11~12.由图11~12可知:残余应力起始累积较快 ,随着循环次数增多,残余应力趋于稳定,与沥青路面工程实际状况相符.
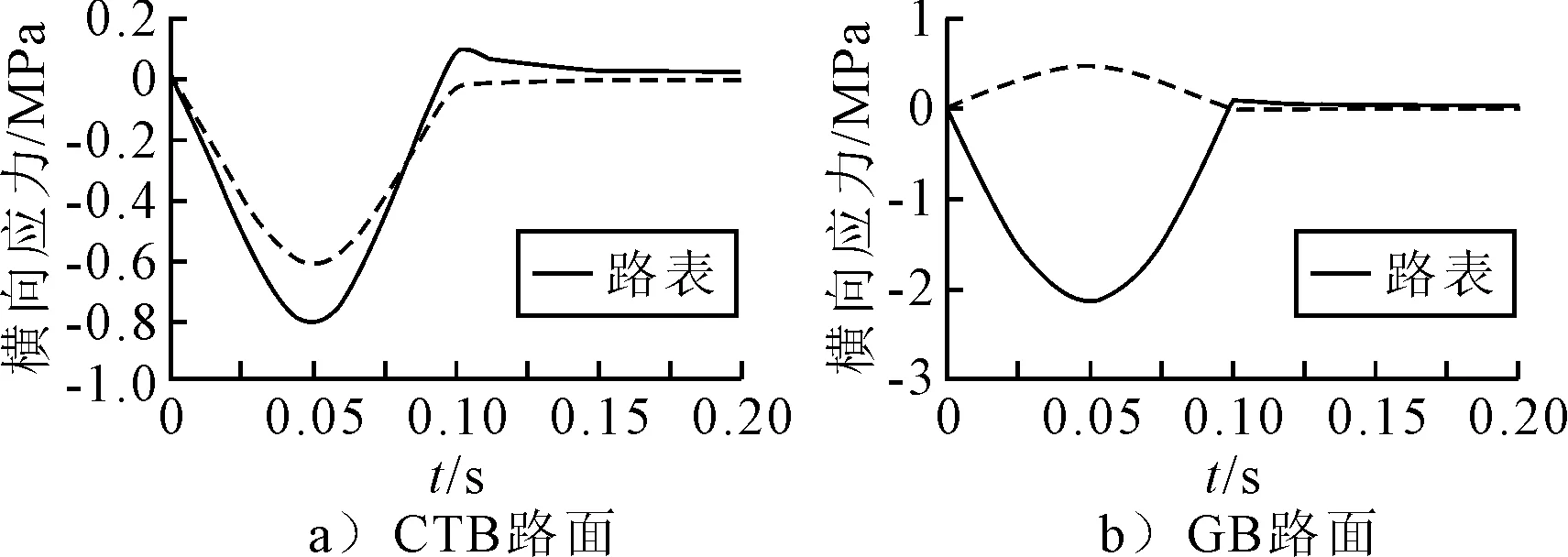
图10 半正弦荷载(单次)横向应力黏弹性响应

图11 CTB路面残余应力

图12 GB路面残余应力
5 结 论
1) 应用广义Maxwell模型和5单元Prony级数,合理定义沥青砂浆及混合料的本构关系,得到有限元松弛试验模拟结果,与真实试验误差不超过1.2%.
2) 应用细观-宏观跨尺度关联机理,结合参数化建模和随机投放算法模拟沥青混合料内部复杂细观几何特征,可以实现从沥青砂浆到沥青混合料的松弛曲线及相关参数预测,相关数值变化规律合理可靠.沥青路面层黏弹性响应分析进一步证明,沥青混合料的跨尺度松弛模量预测可信度高,具有潜在工程适用性与应用前景.
