“三招”学好幂的运算性质

康海芯

幂的运算性质是整式乘法运算的重点内容之一，也是学习的难点。为帮助同学们学好幂的运算性质，本文将从三个方面加以分析，供同学们学习时参考。

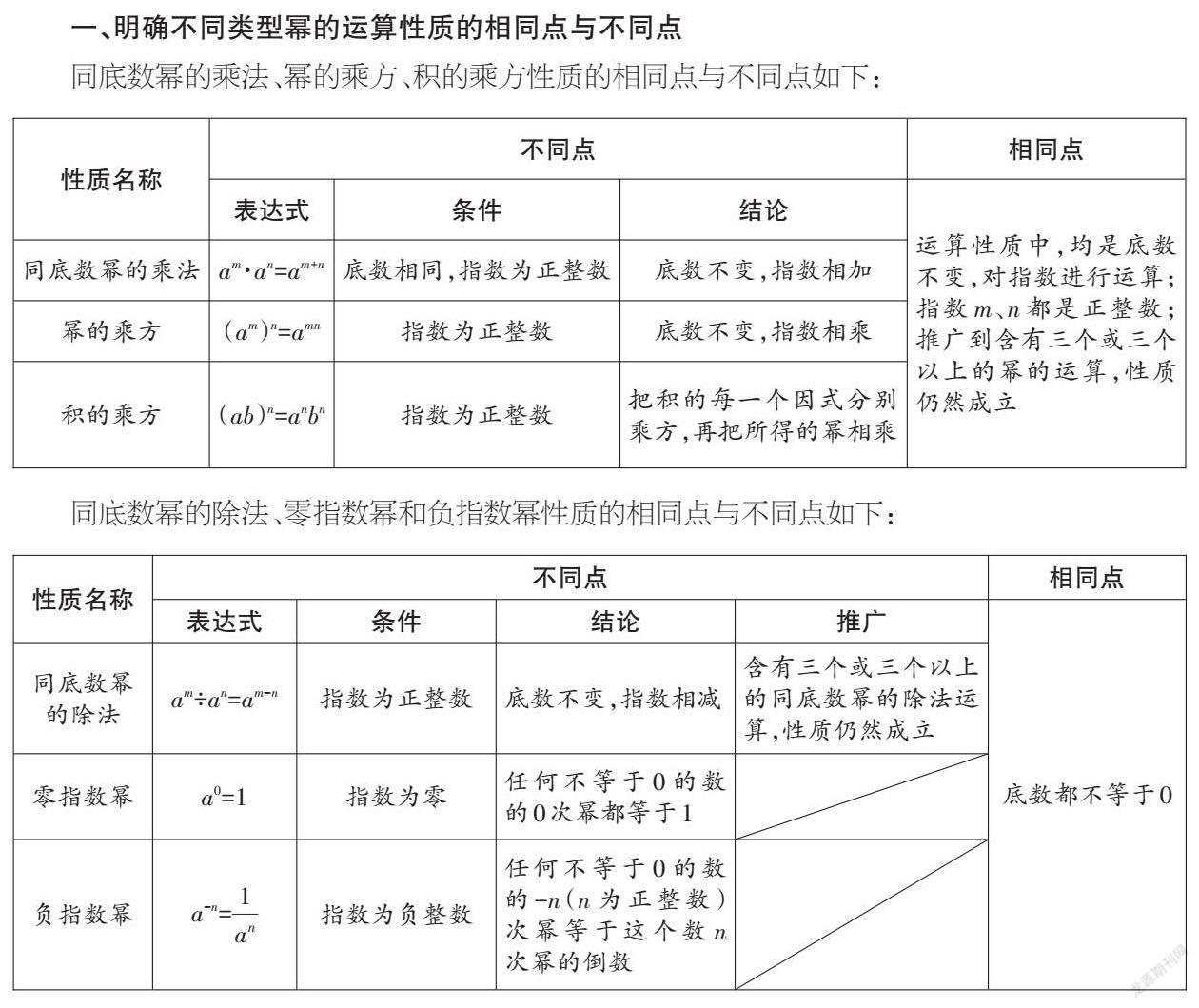
一、明确不同类型幂的运算性质的相同点与不同点

同底数幂的乘法、幂的乘方、积的乘方性质的相同点与不同点如下：

同底数幂的除法、零指数幂和负指数幂性质的相同点与不同点如下：

二、领悟幂的运算性质中字母的内涵

同底数幂的乘法、幂的乘方中的字母a，积的乘方中的字母a、b，既可以表示任意的数，也可以表示单项式或多项式；在同底数幂的除法、零指数幂或负指数幂的运算性质中，底数可以是不等于0的单项式，也可以是不等于0的多项式。底数是多项式时，应看作一个整体。

如计算（x-y）·［（x-y）3］3·（x-y）2，通常把（x-y）看作底数，先运用幂的乘方性质，然后运用同底数幂的乘法运算性质进行计算，可以得到（x-y）·（x-y）9·（x-y）2=（x-y）12。

三、远离幂的运算中“想当然”的错误

学习幂的运算性质时，我们首先应该弄清楚每个运算性质的产生或推导过程，不能只是被动地记憶公式。被动地记忆，我们只能记住它的外形，不能理解性质的本质，当出现与外形类似的公式时，容易与其他性质相互混淆而出现错误。

例如，计算（m-n）3·（n-m）2，许多同学容易出现“原式=（m-n）3·［-（m-n）2］=-（m-n）5”这样的错误。（n-m）2的底数（n-m）换成-（m-n）时，全式应该换成［-（m-n）］2，而不应该等于-（m-n）2。我们把（x-y）n（n为正整数）化成底数为（y-x）的式子时，要根据指数n的奇偶性来判断结果。当n为奇数时，（x-y）n=-（y-x）n；当n为偶数时，（x-y）n=（y-x）n。

其次，我们在运算时，要“识别”每道题运算的类型，包括符号、字母和指数，“联想”到对应的运算性质，尤其要注意领悟不同类型的幂的运算的区别与联系，避免出现不加思考、随意套用运算法则的情形。在平时解题过程中，同学们还应对出现的错误及时究错、反思、总结，找出错误的原因，便可有效避免再次出错。

（作者单位：广东省深圳市龙华中学）