花朵授粉算法研究综述

石 涛，熊 腾，赵玲珠

（江西理工大学 理学院，江西 赣州 341000）

0 引言

花朵授粉算法（Flower Pollination Algorithm，FPA）是由英国学者Yang［1］于2012 年提出的一种智能仿生优化算法，它模拟自然界中花朵授粉原理以求解工程优化问题。在花朵授粉算法中，具有异花授粉算子和自花授粉算子。其中，异花授粉算子是模拟自然界中不同花种之间远距离授粉思想，而自花授粉算子则是模拟自然界相同花种之间近距离授粉机制，两种算子依概率交替执行，从而趋近问题的最优解。自FPA 提出以来，它在边缘计算［2］、图像分割［3］、风速预测［4］、参数估计［5］、目标跟踪［6］、机械优化［7］和神经网络设计［8］等诸多领域中获得了满意的工程结果。

虽然花朵授粉算法被成功应用于许多工程优化问题，然而，在求解一些复杂的工程优化问题时，花朵授粉算法仍然存在着求解精度不足的问题。目前，国内外许多研究人员针对FPA 的不同缺点，提出了一些改进型花朵授粉算法，所作改进各不相同，取得的效果也各有优劣。然而，这些改进思路大致可以从3 个方面进行归纳总结：改进FPA的搜索策略、引入其他优化思想、提出适应性参数控制策略。此外，为了便于工程人员针对不同的工程问题选择合适的FPA 进行寻优，详细介绍5 种具有代表性改进FPA 的主要特征，设计比较试验以评价代表性FPA 的性能优劣，并给出工程应用建议。

1 传统花朵授粉算法

花朵授粉算法具有自花授粉和异花授粉两种形式，是模拟花朵授粉繁殖这一自然现象而产生的一种智能仿生优化算法［1］。在花朵授粉算法中，搜索阶段被分为局部搜索阶段和全局搜索阶段。局部搜索阶段模拟花授粉过程的近距离授粉，即自花授粉现象；而全局搜索阶段模拟花授粉过程的远距离授粉，是通过昆虫、鸟类、蝙蝠等生物进行的异花授粉现象。在算法寻优过程中，局部搜索阶段和全局搜索阶段通过转换概率进行随机切换，从而达到平衡算法局部搜索能力和全局搜索能力的效果。为了模拟自然界中花授粉规律，需依据如下4条规则［1］：

规则1异花授粉现象对应于全局搜索阶段，该阶段传粉者利用Levy分布的特性完成远距离飞行。

规则2自花授粉现象对应于局部搜索阶段，该阶段是在自身邻域范围内完成授粉。

规则3花的常性被表示为繁殖概率，这种概率值与相关联两朵花的相似性成比例关系。

规则4全局搜索阶段和局部搜索阶段由转换概率P∈[0，1]控制转换，因花朵会受到物理位置上的邻近性及风等其他自然因素的影响，在算法中起到重要作用。

应用花朵授粉算法求解D维优化问题时，首先进入初始化阶段，设置种群大小为np，假设在第G 代时个体i在搜索空间中的位置用表示，其中G 是当前代数，i∈{1，2，...，np}，则按式（1）在搜索空间上界和搜索空间下界范围内随机产生np个个体［1］：

其中，j=1，2，…，D代表维度，xmaxj是搜索空间第j维的上界，xminj是搜索空间第j维的下界。

当根据转换概率进入全局搜索阶段时，个体将进行Levy飞行完成长距离跳跃，从而扩大在搜索空间中的寻优范围，具体如式（2）［1］：

其中，UX是由第i个个体产生的新个体，GbestG是第G 代种群中的最优个体，L(λ)是根据Levy分布产生的Levy飞行步长。L(λ)是一个较大的步长，帮助算法模拟花朵的远距离授粉，从而使算法能够搜索到较大范围内可能存在的有希望个体。

当根据转换概率进入局部搜索阶段时，个体模仿花朵授粉中的自花授粉过程，在它所在的局部范围内完成短距离搜索，挖掘自身邻域内可能存在的有希望个体，具体如式（3）［1］：

其中，ε是[0，1]之间的随机数，是从第G 代种群中随机获取的第j个个体是从第G 代种群中随机获取的第k个个体，且j≠k≠i。花朵授粉算法利用两个随机个体的差分向量，对当前个体进行随机扰动，从而在当前个体所在的局部范围内搜索更优秀的个体。

为不失一般性，以求解最小化优化问题为例，FPA 通过转换概率P 实现全局搜索阶段和局部搜索阶段的随机切换，具体搜索过程如算法1 所示，其中f函数表示适应值函数。

算法1FPA伪代码

2 FPA的改进

迄今为止，花朵授粉算法吸引了优化算法研究领域内许多研究者的注意。然而，在求解一些复杂优化问题时，花朵授粉算法存在着一些不足。传统花朵授粉算法在局部搜索阶段由两个随机个体实现局部寻优，缺乏优秀的引导信息，这导致算法的局部搜索能力较弱。此外，传统花朵授粉算法的控制参数由人为设定，这种参数设置并不一定满足算法各演化阶段的需求，导致算法求解性能较差。为了提升花朵授粉算法寻优性能，学者们提出了许多改进型花朵授粉算法，并通过数值实验或实际工程应用检验改进算法的有效性。改进型花朵授粉算法可以按以下3 个改进思路进行归纳：①改进FPA 的搜索策略；②引入其他优化思想；③提出适应性参数控制方法。

2.1 改进FPA的搜索策略

在花朵授粉算法中，全局搜索阶段利用最优个体引导搜索，但最优个体引导可能存在引导过度的问题，并没有采用机制或策略平衡最优个体的引导作用，这导致算法可能陷入局部最优，出现“早熟”收敛现象。局部搜索阶段利用随机个体进行搜索，存在较大盲目性，需要种群中的优秀个体提供明确的搜索方向，以缓解开采能力不足的问题。针对FPA 搜索策略的缺点，许多研究者设计了新的搜索策略，以提升算法寻优能力。

沈艳军等［9］针对传统FPA 在局部搜索阶段存在的搜索方向随机性问题，引入当代最优个体和旧代最优个体为算法提供双重优秀搜索方向，提升了算法的局部寻优性能。此外，还设计了仿嗅觉搜索策略，在个体的邻域内随机产生多个新个体，并利用新个体中的优胜者替换掉当前个体，该操作扩大了算法的搜索范围。Zhou 等［10］认为，传统FPA 基于Levy 分布的飞行过程具有较高随机性，使得算法搜索到优秀解的概率相对较低，因此利用优秀个体对当前个体进行反向映射，得到对立个体，从对立个体和当前个体中选出下一代子个体，从而提升算法寻优能力。此外，为了提升FPA 的局部搜索能力，设计了自适应的邻域贪婪策略，在可行解的邻域内进行贪心搜索。王玉鑫等［11］认为，传统FPA 在引入基于最优解的定向变异策略时，增加了陷入局部极值的概率，因此提出融合随机个体的定向变异策略，在局部搜索阶段增加搜索方向的随机性，同时，在FPA 的全局搜索阶段引入基于随机个体的均匀搜索策略，增强了算法的全局搜索能力。Salgotra 等［12］认为，基于高斯分布的变异策略能更精细地搜索解空间，具有较强的局部搜索能力，而基于柯西分布的变异策略能产生较大的变异步长，从而避免出现“早熟”现象，因此结合两种变异策略，提出一种基于适应性平均变异策略的花朵授粉算法，降低了算法陷入局部最优的概率，提升了算法求解精度。陆克中等［13］针对花朵授粉算法在求解一些问题时收敛精度较低的问题，提出基于量子变异的自适应花朵授粉算法，设计了种群多样性评判机制以维持种群多样性，所提出的算法具有较强的全局搜索能力。Chen 等［14］设计基于个体邻域的学习策略和基于Levy 分布最优解的种群重组策略，增强了算法的全局搜索能力，降低了算法陷入局部最优的概率。肖辉辉等［15］设计精英解变异策略和劣质解变异策略，提出一种具有多策略的花朵授粉算法，保持了种群多样性，提高了算法寻优性能。

2.2 引入其他优化思想

迄今为止，已经产生了许多用于处理优化问题的方法，其中不仅有传统数学方法，还有一些经典优化机制和许多种智能仿生优化算法，这些方法因优化思想不同，而有着各自独特优势。为了增强花朵授粉算法寻优性能，许多研究人员在花朵授粉算法中引入其他优化思想，利用其优势弥补花朵授粉算法的缺点。

如井福荣等［16］受反方向学习机制的启发，提出一种新的花朵授粉算法，在演化过程中的每一代都生成反向种群，并将当前种群与反向种群进行竞争，保留其中的优胜个体到下一代种群中，该方法提升了种群多样性，降低了算法陷入局部最优的概率。肖辉辉等［17］引入复合形法的思想，提出一种改进的花朵授粉算法，利用复合形将种群搜索过程最差的个体反射为一个较优的个体，从而不断迭代引导，靠近最优解，这种方式降低了算法陷入局部最优的概率，加快了收敛速度。Nabil［18］提出基于克隆选择算法思想的花朵授粉算法，采用克隆比率对亲和力高的两个个体进行克隆选择操作，对于搜索空间非常大的复杂问题，所提出的算法具有较强的种群多样性，提升了算法的全局搜索能力。卞京红等［19］提出一种萤火虫优化启发的改进花朵授粉算法，利用萤火虫算法多位置并行的全局随机搜索机制，以增强算法的搜索性能，实验结果表明，所提出的算法具有较快的收敛速度。Arora 等［20］将混沌映射引入到花朵授粉算法中，降低了算法陷入局部最优的概率，提升了算法收敛速度。肖辉辉等［21］受引力搜索算法的启发，采用个体之间的万有引力和FPA 本身的莱维飞行共同实现个体的位置更新，使得个体受莱维飞行和个体间引力的双重影响，从而共享更多种群信息，实验结果表明，所提出方法的寻优性能较好、收敛速度较快。Mahata 等［22］受粒子群优化思想的启发，在花朵授粉算法结构中混入粒子群搜索策略，有效提升了算法求解精度。Chen 等［23］将云变异的思想引入到花朵授粉算法中，不仅加入个体不同特征信息以指导种群的演化方向，还设计了基于云变异方法的授粉中心更新机制。实验结果表明，所提出的方法加快了算法收敛速度。张新明等［24］受小生境技术的启发，将小生境优化思想引入到花朵授粉算法中，提出基于小生境策略的信息共享机制，提升了算法全局寻优能力。Abdel-Basset 等［25］在花朵授粉算法中混合差分进化思想，通过对每代种群进行变异、交叉和选择操作，保持种群个体间互不相同，减小算法陷入局部最优的概率，使得所提出的改进FPA 具有优于传统FPA 的性能。

2.3 设计参数适应性机制

在智能仿生优化算法领域内，设计参数适应性机制已然成为提升算法性能的重要途径。花朵授粉算法中有三个重要控制参数，即转换概率、异花授粉步长系数和自花授粉步长系数，它们由人为设定或者是［0，1］之间的随机数，并不能根据演化阶段的需求设置合适的参数值。因此，许多研究人员根据花朵授粉算法重要参数的性质，设计了参数适应性机制，从而充分发挥花朵授粉算法的潜力。

卞京红等［26］分析了花朵授粉算法的转换概率和局部搜索步长系数对算法性能的影响，设计了参数自适应方法，使得算法全局搜索能力和局部搜索能力能够平衡。San-Jose-Revuelta 等［27］设计一种基于个体适应值熵的参数调整机制，对花朵授粉算法的转换概率进行适应性控制，并将所提出的算法应用于多用户通信环境中的符号检测和信道估计。实验结果表明，所提出的算法能够保持种群多样性，在应用中取得了较好结果。Allamyousrid 等［28］提出基于β 函数的参数调整机制，适应性调整花朵授粉算法的转换概率，提升了花朵授粉算法求解精确度。Fehmi等［29］研究不同混沌映射的特点，并设计基于混沌映射的参数调整机制，适应性调整花朵授粉算法的转换概率和搜索步长。实验结果表明，所提出的算法能够维持一定的种群多样性，降低了陷入局部最优的可能性。Panagiotis 等［30］针对花朵授粉算法重要参数设计离散型参数集合，并采用单级采样协调方法寻找最优参数组合，对重要参数作出调整。实验结果表明，所提出的算法在多个问题上的求解性能都有所提高。Ozsoydan 等［31］设计指数递减步长调整机制，使得花朵授粉算法的全局搜索步长系数和局部搜索步长系数随迭代呈现陡峭衰减或者平滑衰减趋势。实验结果表明，所提出的算法具有优于传统花朵授粉算法的性能。

3 具有代表性的改进FPA

目前，花朵授粉算法已被广泛应用于各大工程领域优化问题，其优化性能已获得普遍认可。本文从搜索策略改进和参数控制改进的角度，选择了5 种具有代表性的改进FPA，它们均采用全局最优个体信息提升算法性能，但对全局最优个体信息的利用方式各不相同。所选择的5 种改进FPA 有：基于精英对立学习的花朵授粉算法（Elite Opposition-Based Flower Pollination Algorithm，EOFPA）［10］、基于全局最优驱动的花朵授粉算法（An Improved Global-Best-Driven Flower Pollination Algorithm，GFPA）［32］、基于动态全局搜索和柯西变异的花朵授粉算法（Flower Pollination Algorithm Based on Dynamic Global Search and Cauchy Mutation，DCFPA）［33］、基于动态步长的改进型花朵授粉算法（Improved Flower Pollination Algorithm，IMFPA）［34］、具有3 个策略的花朵授粉算法（An Improved Flower Pollination Algorithm with Three Strategies，IFPA）［35］。

3.1 EOFPA

2016 年，Zhou 等［10］为了增强花朵授粉算法的种群多样性，提出基于精英对立学习的花朵授粉算法（EOFPA）。传统FPA 中的Levy 飞行步长是一个随机步长，难以搜索到解空间中的优秀可行解。因此，EOFPA 中提出了精英对立学习策略（Global Elite Opposition-Based Learning Strategy，GEOLS），对个体所在区域的对立区域进行搜索，使得算法搜索的未知区域更广，增加搜索到优秀解的可能性。同时，为了增强算法局部搜索能力，在EOFPA 中提出了局部自适应贪婪策略（Local Self-Adaptive Greedy Strategy，LSGS），在当前个体的邻域内扰动搜索，并将LSGS 用于局部搜索阶段。

在EOFPA 中，精英对立学习策略利用最优个体信息，扩展了算法的搜索范围，有助于提升算法的全局寻优能力，增加搜索到优秀解的概率，而局部自适应贪婪策略在当前个体的邻域内扰动搜索，增强了对局部的搜索能力。

3.2 GFPA

2019 年，Supriya 等［32］提出一种全局最优驱动的花朵授粉算法（GFPA）。为了提升算法收敛速度，GFPA 中引入全局最优个体实现对种群演化的驱动作用。与传统花朵授粉算法不同，在GFPA 中依据转换概率P 将整个搜索过程划分为3 个阶段，除依概率执行原有的全局搜索算子和局部搜索算子外，还以一定的概率执行基于全局最优个体的驱动算子。

GFPA 中引入了以最优个体为基个体的搜索策略，这使得算法有一定的机会在最优个体的邻域内进行开采，提升了算法收敛速度。

3.3 DCFPA

2019 年，贺智明等［33］提出基于动态全局搜索和柯西变异的花朵授粉算法（DCFPA）。在DCFPA 中，为了缓解算法在全局搜索阶段过度趋近最优解，避免算法陷入局部最优，提出了动态全局搜索方法，加入了平均最优位置以引导算法搜索方向。此外，为了维持种群多样性，增强算法在搜索后期的寻优性能，在DCFPA 中利用柯西分布的特性对每一代的全局最优解进行贪心式变异更新。

DCFPA 中引入平均最优位置引导个体更新，为算法提供了可靠的搜索方向。同时，分配了一定的计算资源更新最优个体，这有利于提升算法开采能力。

3.4 IMFPA

2019 年，刘国繁等［34］针对花朵授粉算法在搜索后期收敛速度慢和易陷入局部最优问题，提出一种改进花朵授粉算法（IMFPA），并将其应用于优化RSSI 定位。IMFPA 认为在迭代早期需要较大的搜索步长加快收敛，而在迭代后期则需要较小的步长进行精细搜索，因此，提出了基于动态步长的全局搜索算子，设计搜索步长随着迭代而缓慢减小。此外，IMFPA 中认为花朵授粉的局部搜索阶段由两个随机个体引导搜索，具有盲目性。因此，引入全局最优个体到局部搜索算子中，从而为算法搜索提供更明确的方向信息。

IMFPA 的改进主要在于全局搜索算子和局部搜索算子。全局搜索算子中设计了随迭代次数增加而逐渐减小的步长系数，控制了个体的Levy 飞行，提升了演化前期的全局搜索能力和演化后期的局部搜索能力。局部搜索算子中设计了基于全局最优个体的搜索策略，为算法提供更优的搜索方向，从而提升算法收敛速度。

3.5 IFPA

2020 年，Yang 等［35］针对花朵授粉算法在求解一些复杂问题时，求解精度和收敛速度不足的问题，提出具有3个策略的花朵授粉算法（IFPA）。在IFPA 中，为了缓解局部搜索阶段较高随机性导致的搜索效率较低问题，提出双向学习策略（Double-Direction Learning Strategy，DLS），将相邻两代的全局最优个体信息进行融合，用于引导种群演化方向。相比单优秀个体引导，这种多优秀个体融合引导的方式能使种群朝着优越的方向演化，并缓解单优秀个体引导带来的种群多样性锐减情况，从而降低算法陷入局部最优的可能，为算法提供明确的搜索方向。

DLS 被用于局部搜索阶段，提升了算法的局部搜索能力。然而，相邻两代最优个体的相似度较大，甚至可能处于搜索空间中同一位置，所提供的搜索方向信息对缓解算法陷入局部最优的效果有限。为了进一步提升算法逃离局部最优的能力，在IFPA 中提出了贪心策略（Greedy Strategy，GS），并将其引入到全局寻优阶段。GS 中利用两个随机个体信息，对当前个体施加扰动，使得种群向着随机方向进行远距离搜索，增强了算法的全局搜索能力。

此外，IFPA 中设计了转换概率动态调整策略（Dynamic Switching Probability Strategy，DSPS），设置转换概率P 随迭代由0.8 衰减至0.2，使得算法在演化前期执行更多的全局搜索，而在演化后期执行更多的局部搜索。

4 性能比较实验

4.1 实验设计与测试函数

实际上，不同的优化算法有着不同的优势，并不存在一种优化算法能适用于所有优化问题。为了帮助工程人员针对实际问题选择合适的FPA 进行求解，对具有代表性的FPA，即FPA 与EOFPA、GFPA、IMFPA、DCFPA、IFPA，设计性能比较实验。选取智能仿生算法研究领域常用的23个测试函数［36-37］进行比较实验。其中，F1-F13 是单峰多峰函数，F14-F23 是旋转偏移函数。由于单峰多峰函数相对容易搜索到最优解，设置单峰函数和多峰函数的最大评价次数为2 000×D；由于旋转偏移函数的复杂多变性质，设置旋转偏移函数的最大评价次数为10 000×D，具体函数如表1 所示。实验中，设置各算法参数与原文献保持一致，将FPA 和5 种改进FPA 在23 个测试函数上各独立运行30次，得到误差均值和误差标准差，并采用Wilcoxon 秩和检验（显著性水平α=0.05）分析FPA 与EOFPA、GFPA、IMFPA、DCFPA、IFPA 之间的性能优势和劣势。

4.2 实验结果与分析

将FPA 与EOFPA、GFPA、IMFPA、DCFPA、IFPA 在23个测试函数上运行。表2 给出了FPA 与5 种代表性FPA 在测试函数上的比较结果，表3 给出了FPA 与EOFPA、GFPA、IMFPA、DCFPA、IFPA 进行Wilcoxon 检验得出的P 值，当P 值小于显著性水平0.05 时，表明两比较算法间存在显著差异。图1 给出了FPA 与EOFPA、GFPA、IMFPA、DCFPA、IFPA 在部分函数上的收敛图。

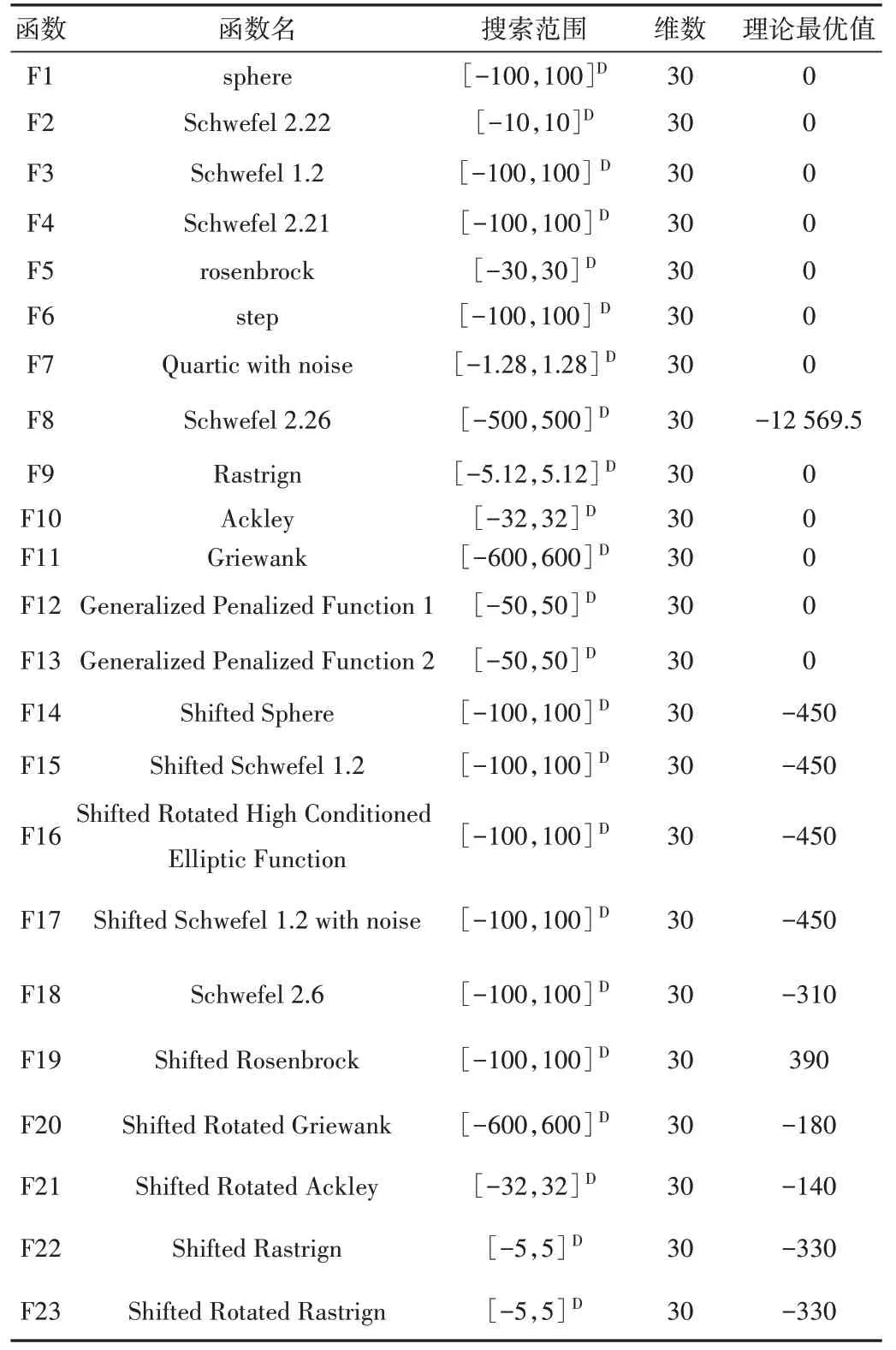
Table 1 23 benchmark function表1 23个测试函数

从表2 可以看出，5 种代表性FPA 算法性能均优于传统FPA。与传统FPA 相比，EOFPA 在20 个函数上结果更优，在1 个函数上结果较差，在2 个函数上结果相似，表明EOFPA 具有相对平衡的局部搜索能力和全局搜索能力；GFPA 在21 个函数上结果更优，在1 个函数上结果较差，在3 个函数上结果相似，这表明GFPA 有效提升了算法收敛速度，同时能够维持一定的种群多样性；IMFPA 在20 个函数上结果更优，在1 个函数上结果较差，在2 个函数上结果相似，表明IMFPA 能够避免算法陷入局部最优；DCFPA 在13 个函数上结果更优，在9 个函数上结果较差，在1 个函数上结果相似，且DCFPA 在单峰多峰函数上取得了较大优势，表明其具有较为优秀的局部搜索能力；IFPA 在17 个函数上结果更优，在2 个函数上结果较差，在4 个函数上结果相似，这表明IFPA 具有更优的求解精度。结果表明，5 种FPA 对搜索策略的改进或者参数控制的改进均有助于提升花朵授粉算法的寻优性能，改进方法是有效的。

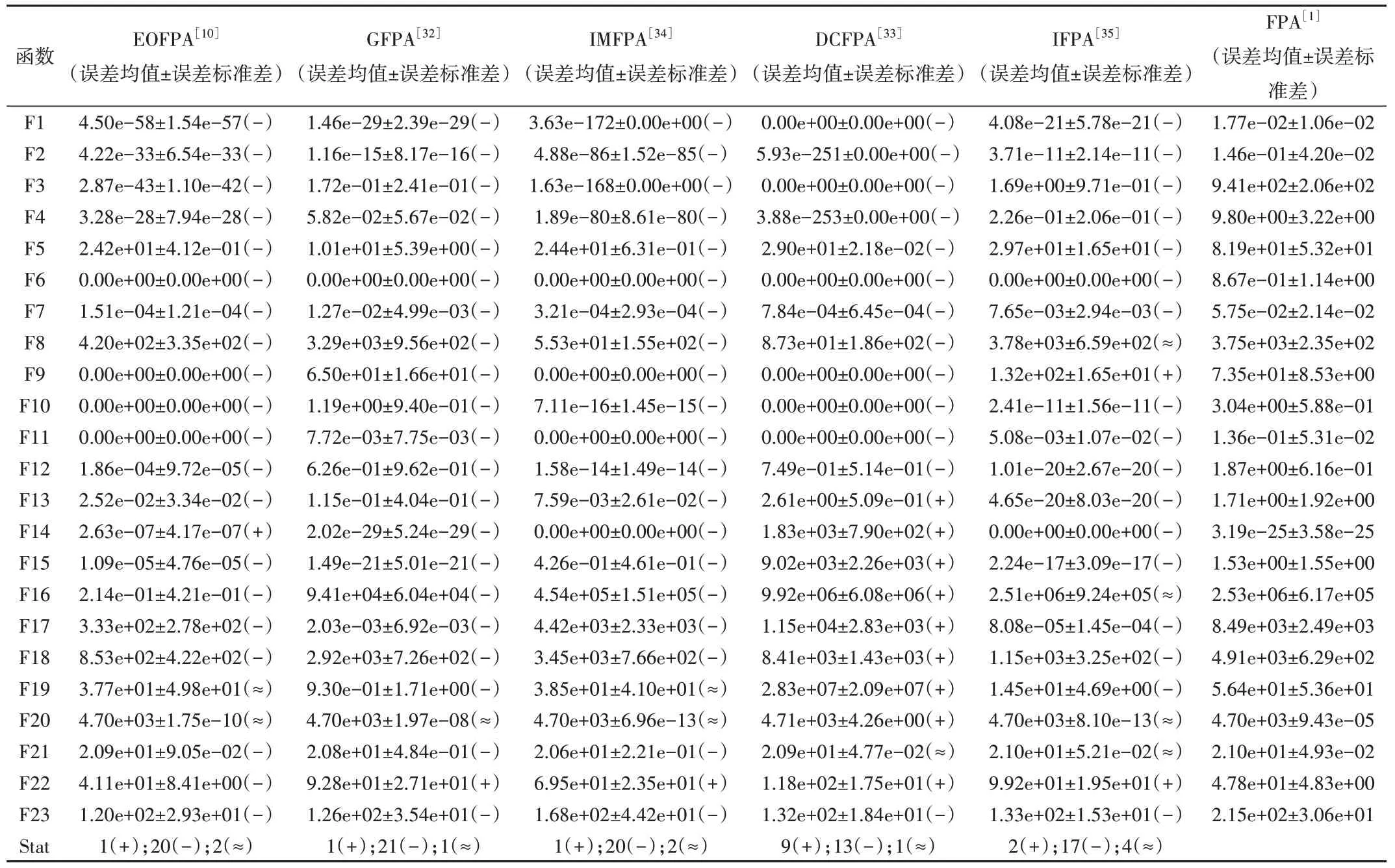
Table 2 Comparison results of FPA with EOFPA，GFPA，IMFPA，DCFPA，IFPA表2 FPA与EOFPA、GFPA、IMFPA、DCFPA、IFPA比较结果

结合表3 给出的Wilcoxon 检验P 值可知，EOFPA、GFPA、IMFPA、DCFPA、IFPA在大部分单峰多峰和复杂函数上都要显著优于传统FPA。从图1可以看出，在单峰函数F1、F2和F3上，DCFPA较具优势，IMFPA次之，其他3种改进的FPA基本上能够取得优于传统FPA的结果。对于多峰函数F9、F10、F12，DCFPA在函数F9和F10上的结果优于其他比较算法，而在函数F12上结果只优于传统FPA；IMFPA 在这3 个多峰函数上的结果具有一定优势，寻优性能较为稳定；EOFPA 在函数F9 和F10 上的寻优性能较为显著，在函数F12 上优于DCFPA、GFPA 和传统FPA，且优势相对较小；IFPA 在函数F9、F10、F12 上寻优性能依次呈现上升趋势，在函数F12 取得了比较算法中最优的结果；GFPA 在这3 个多峰函数上取得的结果优于传统FPA，相比其他改进FPA优势较小。在复杂函数F15、F16、F17 上，EOFPA、GFPA 的寻优性能较为稳定，并分别在函数F16、F15 取得了比较算法中最好的结果；相比其他改进FPA，IFPA在函数F17上取得了最优结果，在函数F15上的寻优性能也具有较大优势，然而在F16 上的寻优结果要差于传统FPA，这表明IFPA 在求解复杂函数时性能不够稳定；相比于求解单峰多峰函数，DCFPA 和IMFPA 在求解复杂函数时性能有较大下滑趋势，取得的结果相似于甚至差于传统FPA。

Table 3 P value of Wilcoxon rank sum test among FPA and EOFPA，GFPA，IMFPA，DCFPA，IFPA表3 FPA与EOFPA、GFPA、IMFPA、DCFPA、IFPA进行Wilcoxon检验得出的P值

综上可知，在面对实际应用中的单峰问题时，运用DCFPA 和IMFPA 求解均能得到较为满意的结果，且IMFPA 的寻优性能比DCFPA 更为稳定；运用EOFPA 也能稳定求解，得到较优结果。在面对多峰问题时，IMFPA 的寻优性能在比较算法中最为稳定；而IFPA、DCFPA 和EOFPA 在求解一些多峰问题能取得较为精确的结果。在面对旋转偏移问题时，GFPA 和EOFPA 求解性能较为稳定，寻优结果较优；IFPA 在求解一些复杂问题时能够取得优秀结果，然而也存在陷入局部极值的可能性。

5 研究总结与展望

Fig.1 Convergence graphs of FPA and five improved FPA on partial functions图1 FPA与5种改进FPA在部分函数上的收敛图

花朵授粉算法作为一种简单实用的智能仿生优化算法，引起了许多研究者的关注。针对FPA 存在的缺点，许多改进型花朵授粉算法被提出，使得算法性能得到一定提升。本文对改进花朵授粉算法进行总结，对5 种具有代表性的FPA 改进算法进行分析，并设计比较实验，直观展示了5 种改进FPA 在性能上的优势和劣势。实验结果表明，这些代表性FPA 适用于求解不同类型的优化问题，如DCFPA 和IMFPA 在求解单峰多峰问题时具有较大优势、GFPA 和EOFPA 在求解旋转偏移问题时效果较好。因此，针对不同的工程优化问题，根据5 种代表性FPA 的性能特点就能选择出最合适的求解算法。

同时可以看出，对FPA 的研究尚处在起步阶段，FPA存在的一些缺点还值得进一步探索改进，总结归纳如下：

（1）FPA 的搜索策略。在FPA 的全局搜索阶段，服从Levy分布的远距离跳跃方法可能导致算法遗漏对有希望未知区域的搜索，应作进一步的精细搜索。此外，仅利用最优个体引导全局搜索，增大了算法陷入局部最优的概率，可考虑多优秀个体集合引导，为算法提供更多可能的搜索方向。在FPA 的局部搜索阶段，基于随机个体的搜索策略为寻优带来了盲目性，导致算法局部搜索能力弱，可考虑利用种群中的优秀信息，为算法提供明确的搜索方向。

（2）FPA 的参数控制。FPA 有3 个重要参数，即转换概率、自花授粉步长系数和异花授粉步长系数，它们对算法寻优性能的影响很大。值得注意的是，参数设置不仅依赖于优化问题的性质，还依赖于算法不同演化阶段的特点。有研究者为FPA 设计了适应性参数控制策略，对算法性能有一定提升。然而，全面结合了优化问题性质和不同演化阶段特点而设计的适应性参数控制策略比较匮乏，尚有待进一步探索。