立铣刀侧铣加工剖分式直齿锥齿轮时的刀位求解
2023-05-11李聚波段新峰房建垒耿瑞广
李聚波,赵 岩,王 斌,段新峰,房建垒,耿瑞广
(河南科技大学 机电工程学院,河南 洛阳 471003)
0 引言
大型锥齿轮广泛应用于发电、船舶、矿山等重要领域。近年来随着大型起重机械、冶金行业、矿山机械等重型机械行业的不断发展,越来越多的厂家对大型直齿锥齿轮的需求日益增多。大型直齿锥齿轮具有结构尺寸大、制齿难度大等特点,其制造能力是先进制造业核心竞争力的集中体现[1-2],剖分式结构已成为现有特大型直齿锥齿轮的常用结构。
针对大型锥齿轮的加工制造,国内相关研究人员对其进行了研究并取得了一定的成果。文献[3]提出了指形铣刀基于刀倾法数控展成准双曲面齿轮的方法,以解决重型准双曲面齿轮加工使用专用机床和大直径刀盘、加工困难和费用昂贵等问题。文献[4]基于等基圆锥齿轮理论,建立了剖分式等基圆锥齿轮的的切削坐标系,求解了加工等基圆锥齿轮的刀位数据,实现了剖分式等基圆锥齿轮的加工。文献[5]通过有限元软件进行仿真分析,探究了剖分式曲线齿锥齿轮在整个加工过程中的应力分布演变规律,研究了切齿过程中轮坯内应力演变的内在作用机理及对其变形产生的影响。文献[6]通过建立直齿锥齿轮剖分轮坯刚度变化-残余应力演变-变形映射关系的模型,研究了剖分式直齿锥齿轮在加工过程中的变形情况。文献[7]基于石油钻机转盘参数,采用将大锥齿圈剖分为等 90°的 4 块的方式,设计了一种大型锥齿圈,并在 ANSYS软件中对其进行了受力分析。文献[8]提出一种剖分式大直径薄壁内齿圈的加工技术,对解决剖分式无间隙薄壁内齿圈变形的工艺方法进行了综合分析和研究。文献[9]针对剖分式大型齿轮齿形的实际生产加工中,常出现的缺乏适用加工刀具的问题,提出一种通过使用小于剖分式大型齿轮模数的可转位盘形齿轮铣刀的方法进行齿轮齿形的粗加工。文献[10]针对大型分体式硬齿面齿圈进行了加工工艺分析论述,采用硬质合金滚刀刮削淬火后大齿轮的工艺方案,提高了齿圈的制造精度。文献[11]从制造工艺、夹具设计、关键技术等方面,论述了剖分式大型圆柱齿轮的制造技术。文献[12]针对特大型剖分式圆柱齿轮的加工变形,从毛坯热处理、加工工艺、装配运输等多个方面,给出了防止变形的具体措施。文献[13]以直径9 139 mm的四半分体结构大齿轮的加工制造为例,对此类大直径、分体结构的大齿轮加工难点进行了分析,并根据以往实际制造经验结合实际情况,给出了基本解决方案,为特大型剖分齿轮的加工提供了经验和参考。文献[14]提出了利用立式数控铣齿机代替卧式铣齿机,实现大型等基圆锥齿轮加工的方法,并通过切齿加工仿真验证了所提方法的可行性。文献[15]对采用指形铣刀成形法铣削特大型直齿锥齿轮进行了研究,分析了中间模数法和设计配对法对加工齿形的影响。文献[16]提出一种特大型直齿锥齿轮齿面的包络刨削加工方法,通过调整刨削次数对包络精度进行控制,提高了加工精度。文献[17]利用球头铣刀在立式数控铣床上加工大型直齿锥齿轮,提高了加工效率。文献[18]采用指形铣刀在大型数控立式铣床上加工大模数直齿锥齿轮,并采用渐开线模数铣刀对齿面进行修形,得到了较为理想的齿形面。文献[19]针对特大型直齿锥齿轮,提出将大轮的齿面以直廓齿面代替传统的渐开线齿面的方法,提高了特大型直齿锥齿轮加工效率,但是存在需要对相应小轮齿面进行拓扑修形的缺点。
上述研究成果为大型直齿锥齿轮的加工提供了新的方法思路,对于提升大型直齿锥齿轮的生产效率和加工精度具有积极的意义。但所使用的加工刀具是专用的成形铣刀或者球头铣刀。成形铣刀制造难度大,且所加工的齿面为近似理想曲面。同时,使用球头铣刀加工大型齿轮效率太低。此外,基于成形铣刀或球头铣刀的加工方法,对加工设备要求高,需要使用大规格机床才能完成齿面的加工。而通用立铣刀价格低廉,加工效率高、范围广,同时一般尺寸规格的通用数控机床技术成熟,在齿面加工中应用广泛[20-22]。鉴于此,本文提出基于立铣刀的剖分式直齿锥齿轮数控切齿方法,在分析立铣刀侧铣加工可行性的基础上,建立了剖分轮坯侧铣加工齿面时的坐标系,规划了加工路径,完成了数控加工中的刀位求解。通过仿真切齿、实际加工及齿面检测,验证了立铣刀侧铣加工剖分式直齿锥齿轮时刀位求解方法的正确性。
1 齿面侧铣加工分析
当立铣刀沿着直齿锥齿轮齿面进行切削时,刀具的位置由一系列的刀心坐标M及其对应的刀轴矢量P来确定,同刀轴矢量P与对应的齿面法矢量N之间是垂直的关系。刀心坐标决定了刀具的空间位置,刀轴矢量决定了刀具在刀心坐标处的方向和姿态。立铣刀侧铣加工示意图如图1所示。
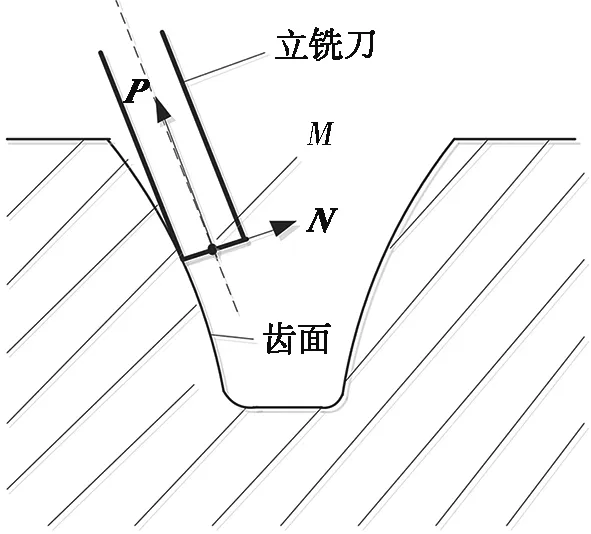
图1 立铣刀侧铣加工示意图
使用传统方法加工齿轮时,齿轮的旋转中心往往与机床的回转工作台中心重合,随着工作台规律地转动,加工每个齿槽时的刀具位置不断重复,能够将全部的齿轮齿槽加工出来。剖分轮坯及机床工作台的位置关系图如图2所示,此时,剖分齿轮轮坯的中心与机床的回转工作台中心有一定的距离,使得加工每个齿槽的刀具位置及姿态各不相同。
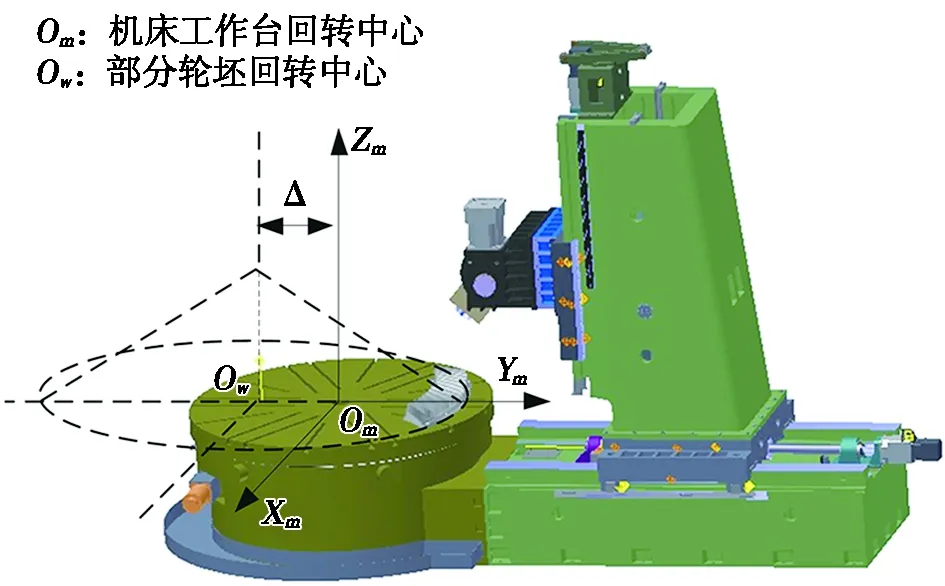
图2 剖分轮坯及机床工作台的位置关系图
根据直齿锥齿轮的齿形特点,粗加工时采用成形法加工,使用指形铣刀等成形刀具。本文研究的立铣刀侧铣针对的是齿面的精加工。
加工开始时,刀具表面与理论齿面相切,从齿轮的顶端开始,立铣刀先由大端开始沿着齿轮圆锥母线进行切削,移动到齿轮的小端。然后,由小端到大端进行切削,刀具来回往复,呈Z字形的走刀轨迹,直到将整个齿面加工完成,精加工的走刀轨迹规划如图3所示。采用这种路径加工时的刀位点计算相对比较容易,而且刀具沿着齿面母线移动,齿面的加工精度及齿面加工后的刀纹更易于控制。刀具之间间隔距离的选择根据加工精度、齿面光洁度要求确定。同时,Z字形的走刀轨迹也减少了刀具空行程的时间,从而提高了生产加工效率。对于整体式直齿锥齿轮的齿面加工,可以在UG软件里进行自动加工编程,但是此时生成的加工路径与人工编程规划的路径不同。对于剖分式直齿锥齿轮,其几何中心落在机床之外,如果要在UG软件里面进行自动加工编程,难度会大很多。
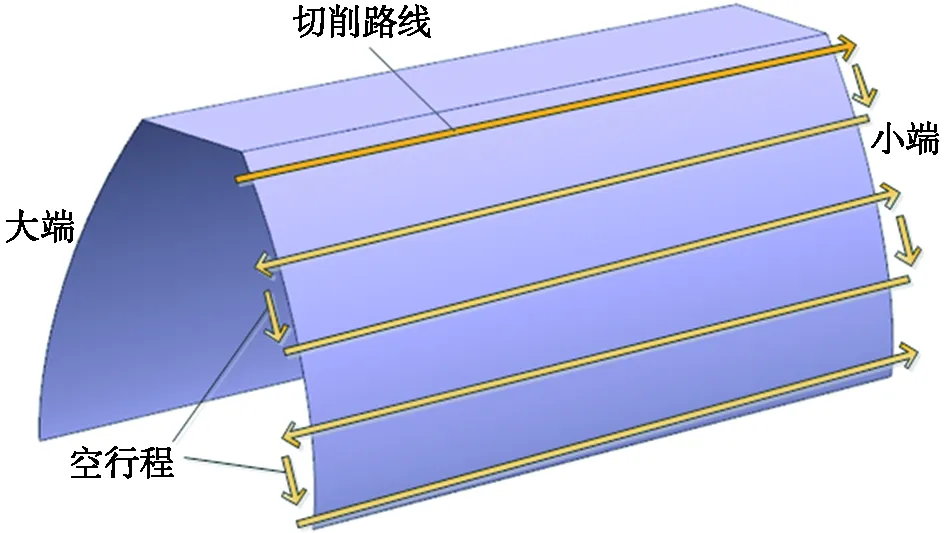
图3 精加工的走刀轨迹规划
2 侧铣加工刀位的求解
根据侧铣加工齿面的成形特点,建立如图4所示的剖分加工坐标系:

图4 剖分加工坐标系
SO(OO~Xo,Yo,Zo)为与轮坯相连的坐标系,原点位于剖分轮坯基圆锥的锥顶O,Z轴通过基圆锥底部圆心。通过求得轮坯坐标系下的所有刀心坐标、刀轴矢量,得到剖分式加工中刀具的空间位置和姿态。
Sc(Oc~ic,jc,kc)为固连于刀具的坐标系,原点为刀心坐标,为瞬时刀轴矢量的方向,用来表达一系列刀具特征点的运动和刀具的偏转角度。
根据直齿锥齿轮的齿面方程,可以将直齿锥齿轮理论齿面看作由一条曲线按照一定的运动规律扫掠得到的曲面,从其几何意义来说,这个曲面被称为直纹面,直纹面是由直线连续运动轨迹所形成的曲面,如图5所示。直纹面的一般表达形式如下[23-24]:
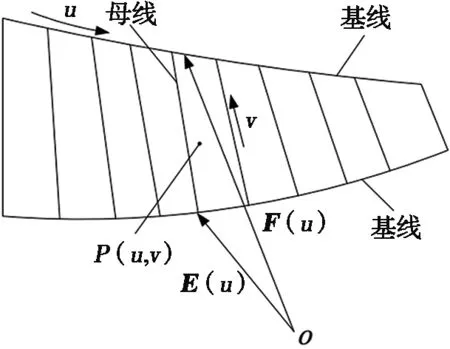
图5 直纹面的形成
P(u,v)=(1-v)E(u)+vF(u),
(1)
其中:E(u)为下基线向量;F(u)为上基线向量。
直齿锥齿轮齿面的大端和小端可看成是两条基线,这两条基线上的等参数点之间的连线即圆锥母线,所以直齿锥齿轮的齿面用直纹面的形式来表达[23-24]:
S(r,φ)=(1-r)W(φ)+rQ(φ),
(2)
其中:W(φ)为小端齿廓方程;Q(φ)为大端齿廓方程;r的取值为[0,1]。
图6为直齿锥齿轮齿面形成示意图,刀心坐标的位置由齿面法矢量和立铣刀半径的大小共同决定,求解刀具的刀心坐标,需要先求出齿面上每一点所对应的法矢量。

图6 直齿锥齿轮齿面形成示意图
根据求得的直齿锥齿轮齿面方程,分别对齿面r、φ两个不同的方向求偏导运算,能够得到齿面上每一点处2个不同参数方向的切向量:
(3)
(4)
其中:
根据空间几何原理,两个向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则,对Sr,Sφ进行向量积运算,使用右手定则确定向量积的方向,能够得到齿面上每一点处的法矢量:
Fs=Sr×Sφ=[fx,fy,fz],
(5)
其中:fx=SrySφz-SrzSφy;
fy=SrzSφx-SrxSφz;
fz=SrxSφy-SrySφx,
法矢量Fs与Sr,Sφ分别垂直,并与Sr,Sφ所处的平面垂直。根据立铣刀的刀具曲面成型特点可知,在使用立铣刀侧铣加工时,刀心坐标所在的位置即理论齿面点沿着齿面单位法矢量的方向偏置一个刀具半径的距离。对齿面法矢量进行单位化即可得到齿面单位法矢量:
(6)
根据齿面方程,可以求得齿面点坐标(X,Y,Z),刀具半径用Rd表示,齿面点坐标同时乘以对应的齿面法向量和铣刀的刀具半径长度,可以求出立铣刀侧铣加工直齿锥齿轮的刀心坐标:
(7)
刀轴矢量决定了立铣刀在空间所处的位置姿态,刀轴矢量和刀心坐标共同决定了刀具的准确位置。根据立铣刀侧铣加工曲面原理可知,当立铣刀沿着刀心轨迹移动时,刀轴矢量垂直于刀心轨迹所形成的的直线。
在工件坐标系下,向量Sr的方向与刀心轨迹所形成直线的方向保持一致,所以可以把向量Sr的方向定义为初始刀轴矢量的方向,再将初始刀轴矢量绕Y轴顺时针转动90°得到实际的刀轴矢量,定义实际的刀轴矢量为P=(px,py,pz),通过坐标转换可得P=Moc·Sr。
其中坐标变换矩阵为:
通过矩阵运算,得到刀轴矢量为:
(8)
3 加工仿真
为了验证上述刀位求解的正确性,根据数控加工原理,对刀轴矢量进行后置处理,然后进行数控加工编程,借助VERICUT[25]软件进行齿面加工仿真,剖分式直齿锥齿轮基本参数见表1。

表1 剖分式直齿锥齿轮基本参数
为了提高加工效率,先通过三轴数控机床完成剖分式直齿锥齿轮的粗开槽,粗加工采用成形法,使用指形铣刀进行齿槽铣削,由于其精度要求低,加工简单,不是本文的研究重点。在VERICUT软件中,建立符合刀位求解及后置处理要求的机床模型如图7所示。设置刀具参数,加载计算得到数控加工程序,精加工仿真过程如图8所示。
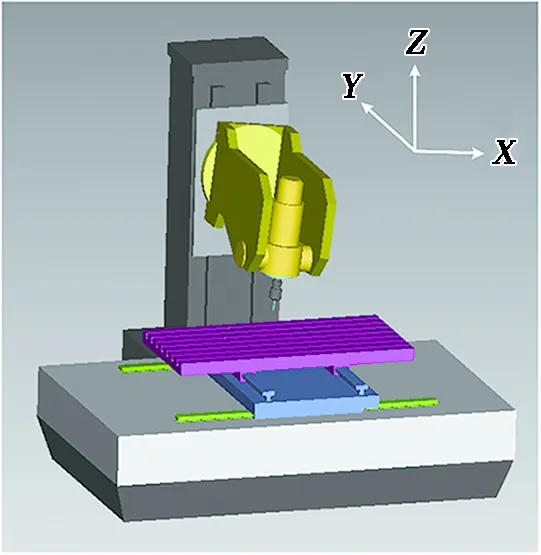
图7 机床模型

图8 精加工仿真过程
完成所有仿真加工后,利用VERICUT 软件的自动比较功能,将标准的预先建立的剖分式直齿锥齿轮的设计模型导入到VERICUT软件中,合理设置过切、欠切对比公差为0.05 mm,自动比较结果如图9所示。由图9可知:在立铣刀加工的齿面上,以点的形式存在欠切现象,齿面存在局部少量残留,齿轮大端锥距处存在少量局部过切,其余部分与理论齿面一致。齿槽底面的欠切,是由于齿槽底面没有进行精加工。仿真结果表明,使用立铣刀侧铣加工剖分式直齿锥齿轮的加工方法正确可行。

图9 VERICUT软件自动对比分析结果
4 加工及测量实验
为了进一步验证计算结果的正确性,在DMU100五轴联动数控机床上进行了直齿锥齿轮齿面切削加工实验。精加工之前,先用指状铣刀进行粗加工,保留精加工余量0.1 mm,再使用φ10 mm立铣刀进行了直齿锥齿轮齿面的精加工。
齿面精加工完成后,使用海克斯康三坐标测量机对其齿面进行了测量。在测量前需要进行相关参数设置,先在三坐标机中建立齿轮测量坐标系,进行基准面的拟合,将工件放置位置的底面设为测量定位基准面,并设置坐标系的原点与剖分轮坯的原点一致。使用海克斯康自带软件的编程语言编制齿轮测量程序,设定测量路径,通过运行齿轮测量程序,测量并获得齿面真实数据,得到测量点坐标值。三坐标齿面测量如图10所示。

图10 三坐标齿面测量
通过自主开发的程序对测量数据进行整理,将理论值与实测值进行对比分析,并将数据转换为衡量齿轮测量的参考值,齿廓偏差结果如图11所示。图11中,1,3,5,6分别为被测齿在整个齿轮中的次序。由图11可知:被测齿轮的齿廓总偏差最大偏差Ff为5.6 μm,齿廓形状公差最大偏差ff为2.6 μm。
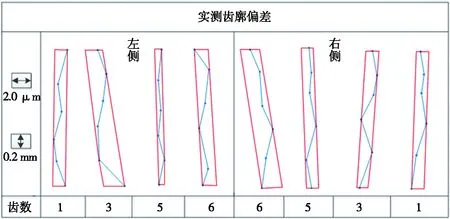
图11 齿廓偏差分析结果
齿距极限偏差结果如图12所示,被测齿轮的齿距极限偏差值fpt为25.3 μm。
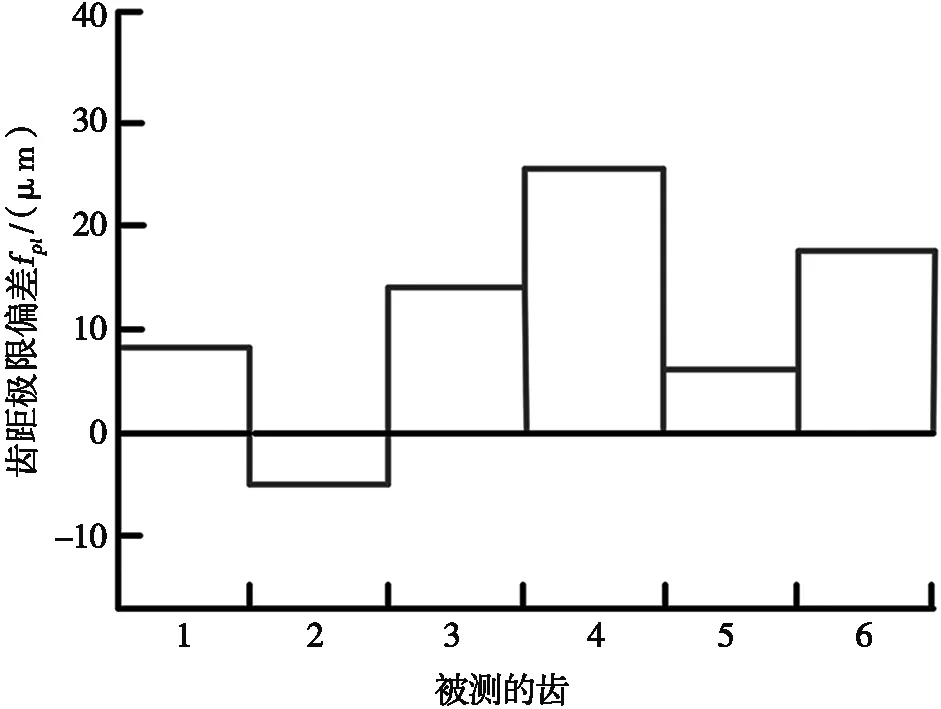
图12 齿距极限偏差结果
齿距累积偏差结果如图13所示,被测齿轮的齿距累积总偏差Fp为21.8 μm。

图13 齿距累积偏差结果
径向跳动偏差结果如图14所示,被测齿轮的径向圆跳动偏差Fr为38.3 μm。
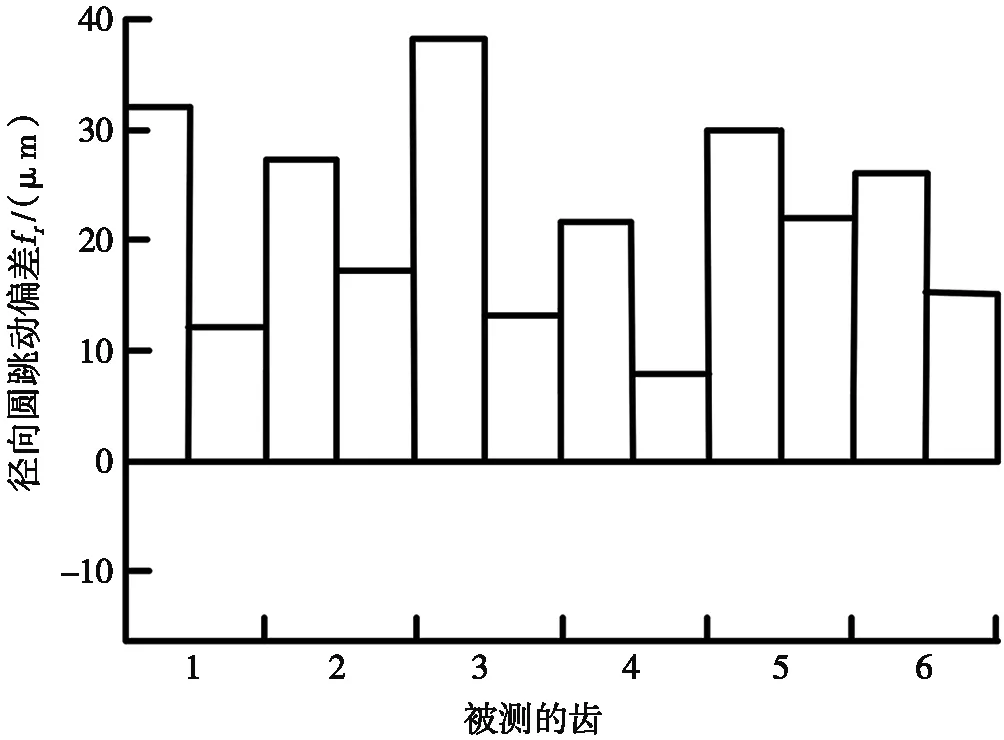
图14 径向跳动偏差结果
通过对图11~图14的测量结果和偏差值分析可知:所有加工偏差值按照机械设计手册所规定的标准,均在正常的范围之内,达到了GB/T 10095.1[26]的7级和规定的特大型直齿锥齿轮的精度标准。
5 结论
(1) 用立铣刀侧铣方法,可以精加工剖分式直齿齿锥齿轮,这为特大型剖分式直齿锥齿轮的制造提供了一种新的可能。
(2) 基于立铣刀侧铣加工时的刀位计算、后置处理数学模型正确,加工路径规划可行。
(3) 该研究可实现在小型机床上加工特大型齿轮,能够极大降低大型直齿锥齿轮制造成本,具有一定的工程应用价值。
