Ti-Zr-Nb 固溶体合金动态压缩强度的机器学习模型优化

李树奎，樊博建，刘兴伟，司胜平，刘爽，谢如玥，刘金旭,3

（1.北京理工大学 材料学院，北京 100081；2.深圳北理莫斯科大学 材料系，广东，深圳 518172；3.北京理工大学 冲击环境材料技术国家级重点实验室，北京 100081）

钛基固溶体合金因具有密度低、耐腐蚀性能和低温性能好、抗疲劳和蠕变性能好等特性以及优异的综合力学性能，在航空航天[1-2]、船舶制造[3-5]、生物医学[6-7]、武器装备[8-9]等领域具有广泛的应用前景.其中，Ti-Zr-Nb 系固溶体合金优异的强塑性匹配及撞击释能特性，在杀爆战斗部毁伤元及聚能战斗部药型罩等领域备受关注.其固溶体的特殊结构既可保证元素的氧化释能活性，又可通过固溶强化实现合金强度的提高，已经逐渐成为国内外研究的热点.YAN 等[10]制备了一种单相BCC 相的Ti-Zr-Nb 中熵合金，兼具良好的杨氏模量(62 GPa)及强塑性，屈服强度657 MPa、拉伸断后延伸率达21.9%；XU 等[9]成功制备了微量O 掺杂的Ti-Zr-Nb 固溶体合金，其静态压缩强度可达1 300 MPa.然而，在战斗部领域的应用中，研究者们更加关注的是毁伤元材料在高应变率加载条件下的动态力学性能.徐雪峰等[11]研究了Ti6321 合金不同组织对其在高应变率加载条件下的动态损伤和断裂行为的影响，结果表明双态组织的Ti6321 合金具有较低的绝热剪切敏感性；张静等[12]研究了高应变率加载条件下加载时间对Ti-6Al-4V 绝热剪切带的影响，发现随入射波加载时间的延长，绝热剪切带变宽.然而，当前关于Ti-Zr-Nb 系合金在高应变率加载条件下的动态力学性能的研究却鲜有报道，其动态力学性能的影响因素尚不明确.

此外，在传统材料设计理念中，新材料的制备与表征需要较长周期，而对于多元合金而言，其成分设计空间大，同时材料力学性能的影响因素复杂，若采用试错法进行材料设计，可能会消耗大量人力物力，且新材料研发效率低下[13].近年来，机器学习作为人工智能的一个重要分支，在材料科学领域已经开展了较为广泛的研究.机器学习方法不仅可以快速处理批量数据，还可以识别人脑无法识别的多维空间参量，瞬间抓准“主要矛盾”，因此，当前机器学习在材料领域研究最为广泛的应用便是针对材料属性的预测.WEN 等[14]采用机器学习方法建立了一套完整的合金设计研究框架，准确实现了Al-Co-Cr-Cu-Fe-Ni 高熵合金硬度的预测，并在预测结果基础上成功制备出了17 种硬度高于原始数据集10%的新合金.ISLAM 等[15]运用带两个隐藏层的神经网络分类模型成功预测了多元合金相形成，平均预测精度可达83%.HUANG 等[16]在此基础上，构建了更加庞大的数据库，同样运用神经网络分类模型预测了高熵合金相形成准则，并构建了相关图谱.此外，将机器学习与现有的理论计算方法结合，可加速材料理论模拟工作的进展.KIM 等[17]运用改良的决策树算法及第一性原理计算对Al-Co-Cr-Fe-Ni 高熵合金弹性性能进行了预测，两者得到的结果与实验结果吻合度较高，即该模型对预测高熵合金弹性性能适用.

在前期研究中，作者已经借助机器学习研究手段，针对Ti-Zr-Nb 合金的准静态压缩力学性能开展了主控参量筛选及重要度排序的相关研究[18]，明确了Ti-Zr-Nb 合金准静态压缩力学性能的主要影响因素.而在当前的研究中，对于材料在高应变率加载条件下的动态力学性能的机器学习相关研究还鲜有报导，基于此，本文将通过粉末冶金高通量制备及材料动态力学性能表征与机器学习方法相结合，针对Ti-Zr-Nb 合金的动态压缩强度的影响因素开展研究，揭示其材料主控参量，为基于材料动态力学性能调控的Ti 系多元固溶体合金成分设计与优化提供高效的研究方法.

1 研究方案与研究方法

1.1 材料制备与性能测试

制备Ti-Zr-Nb 三元固溶体合金所要用到的原料粉包含纯度为99.9%、粒径为10 μm 的Ti 粉、Zr 粉及Nb 粉.本研究所设计的Ti-Zr-Nb 合金的成分范围为Ti: 质量分数10%～60%, Zr: 质量分数20%～70%, Nb:质量分数20%～50%，具体成分点如图1(a)所示.

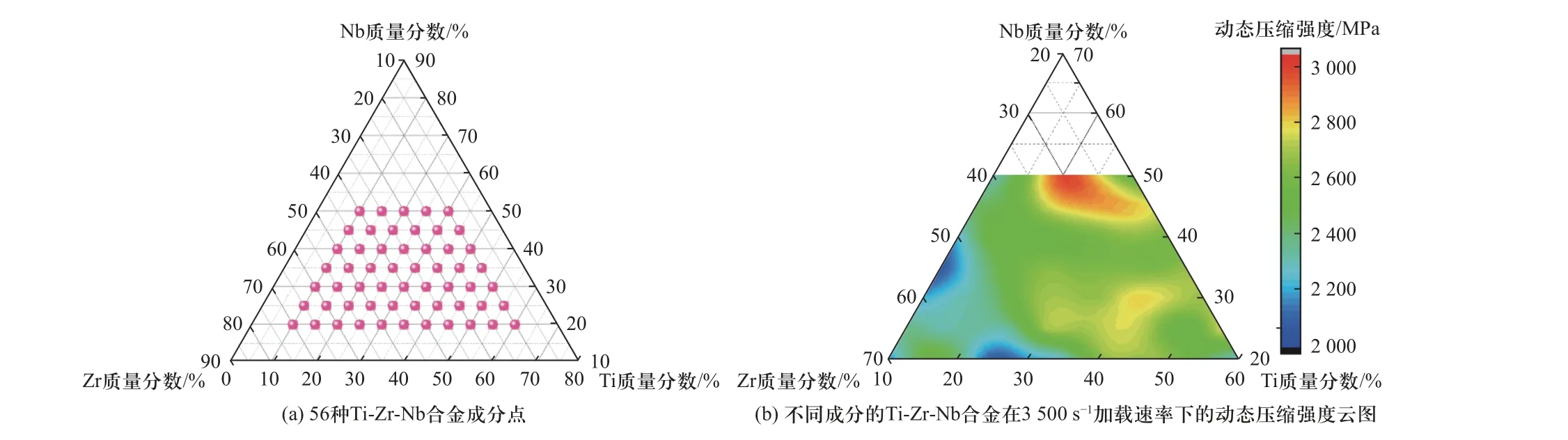
图1 合金成分及力学性能Fig.1 The composition and mechanical properties of alloys

本研究所采用的粉末冶金制备工艺主要包括混粉、压制成型、烧结3 个步骤：①混粉.采用高能球磨法快速制备具有不同成分的Ti-Zr-Nb 合金.球磨具体工艺参量为：转速为200 r/min, 球料比为3∶1，球磨时长为6 h；②压制成型.采用冷等静压工艺压制成型.控制成型压力为400 MPa，保压时间为30 min；③烧结.将压制成型的生坯置于Ar 气氛下进行常压固相烧结，烧结选用的是钼带真空气氛烧结炉设备.烧结时将生坯埋在氧化锆砂下，烧结温度为1 600 ℃，保温时间为4 h.所制备的合金样品致密度均在97%以上.

本研究采用分离式霍普金森压杆(SHPB)对合金的动态压缩强度进行了测试.实验中所用到的测试试样为尺寸φ5 mm×5 mm 的圆柱.每种成分合金进行3 组力学性能测试，取平均值标记为该合金的动态压缩强度，如图1(b)所示为3 500 s-1应变率下合金成分-动态压缩强度图谱.

1.2 机器学习数据库构建

结合文献调研与前期研究，挑选了多元合金中可能影响材料动态压缩强度力学性能的14 组特征参量，如表1 所示.这些参量中包含了影响材料相构成的关键参量，如：元素之间电负性差(Δχ)、价电子浓度(VEC，后文中以CVE表示)，混合焓(ΔH)、混合熵(ΔS)以及Λ参量(与ΔS和δr有关的混合参量)；此外，还包括在各种强化理论中反映晶格失配、模量失配以及位错运动的参量，如考虑间隙氧原子的原子半径错配(δr)与电负性错配(Dχ)，以及不同强化模型中的剪切模量错配(δG、DG)；还包括在J-C 模型中应变率硬化及热软化的影响参量，如剪切模量(G)、密度(ρ)以及熔点(Tm)、热导率(λ)、比热容(CV)等.据此，经初步筛选与优化，获得了潜在影响Ti-Zr-Nb 固溶体合金动态压缩强度的14 个特征参量，构建了影响Ti-Zr-Nb 固溶体合金动态压缩强度的初始特征集.

表1 中，Ci、ri、χi、CVEi、Gi以及Tmi、λi、CVi分别对应合金组成元素的摩尔比、原子半径、电负性、价电子浓度、剪切模量以及熔点、热导率、比热容.Δ为i和j两种元素之间的混合焓.

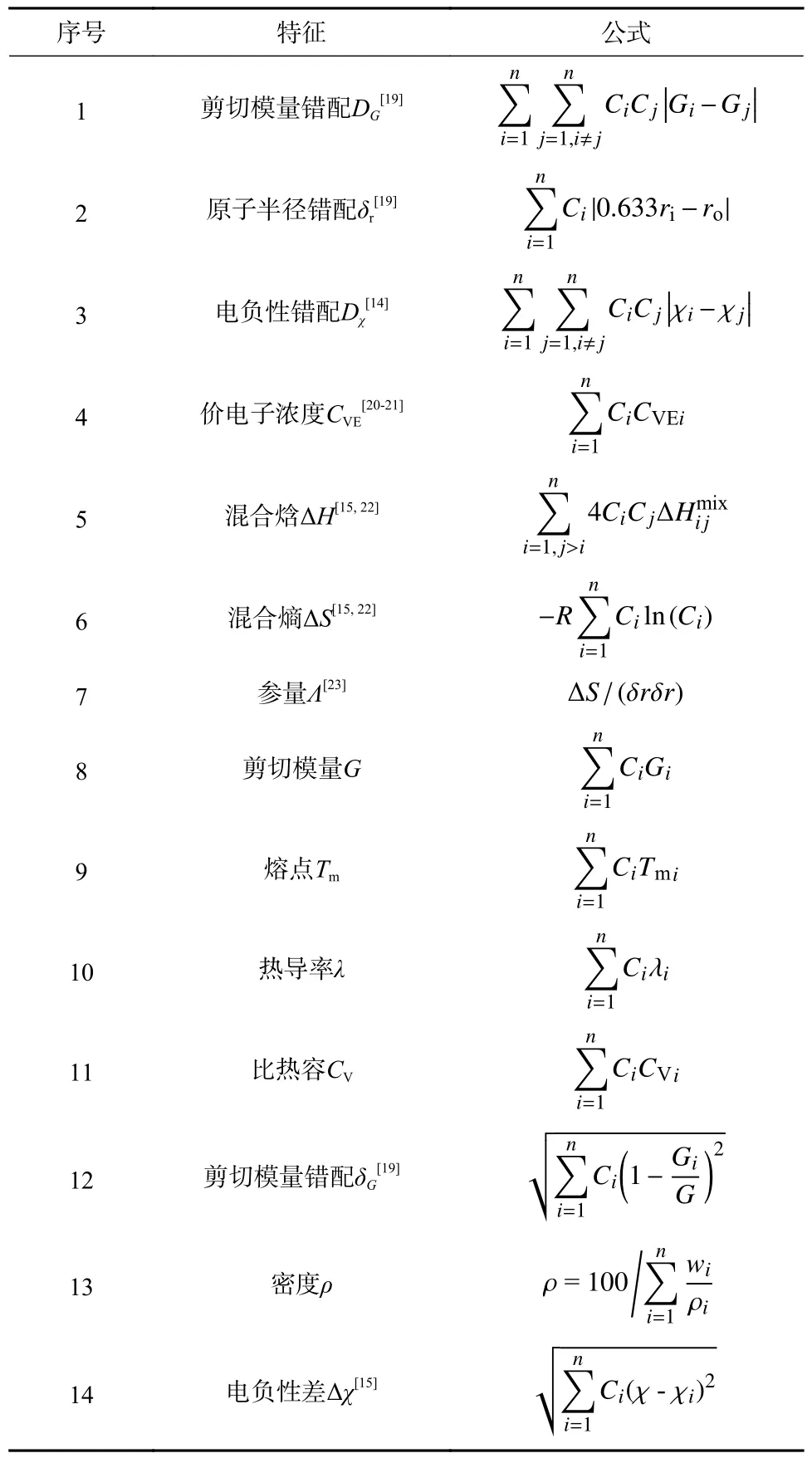
表1 初始特征集Tab.1 The original feature pool

各元素参量如表2 所示，值得注意的是，在粉末冶金制备Ti-Zr-Nb 合金过程中，引入了微量的O 元素，实现了合金强度的提高.前期研究表明，O 元素以2 价离子态存在于Ti-Zr-Nb 合金的八面体间隙中[18]，因此，在计算O 相关参量时，将O 视作离子态计算.同时，使用氧氮氢分析仪对Ti-Zr-Nb 固溶体合金的氧含量进行测试，结果显示Ti-Zr-Nb 系固溶体合金中的氧原子占比在4%左右浮动，因此在考虑氧原子占比计算时，将氧原子占比视为4%计算.

表2 元素参量[18]Tab.2 The parameter of different elements[18]

1.3 机器学习模型及评估方法

选择合适的机器学习模型算法是构建机器学习系统的关键步骤之一，不同的机器学习算法针对不同情况对预测误差及泛化能力具有很大的影响.因此，为筛选针对Ti-Zr-Nb 合金动态压缩力学性能的预测具有最优表现的机器学习算法模型，开展了机器学习模型筛选工作.

本节共选用了线性回归（lin）、带高斯核的支持向量回归（svr_rbf）、带线性核的支持向量回归（svr_lin）、带多项式核的支持向量回归（svr_poly）、多层感知机（mlpe）及随机森林回归（rfr）等6 种常见的机器学习算法，以Ti-Zr-Nb 合金的动态压缩强度作为目标性能，构建机器学习模型，并从中选择针对合金动态压缩强度预测的最优算法.

在进行模型计算前，使用StandardScaler 方法对初始输入特征集进行了标准化处理，经过处理后的数据符合标准正态分布，即均值为1，标准差为0，计算方法如式(1)所示

式中：X*为 经标准化处理后的数据；为所有样本数据的平均值；σX为所有样本的标准差.在每次模型计算时，均会通过留出法（hold-out）随机地将初始数据集划分为训练集以及测试集，训练集用于训练机器学习模型，测试集则用于验证模型的泛化能力.选用的误差评估指标为平均绝对误差EMAP(mean absolute percentage error)以及衡量回归模型拟合程度的决定系数R2，EMAP越小，R2越接近1，则说明机器学习模型效果越好，计算公式分别如式(2)、式(3)所示

2 结果与讨论

2.1 机器学习模型筛选

基于Python 编译语言中的Scikit-Learn 模块，调用了上述6 种机器学习算法，并通过程序计算，分别获得了6 种机器学习模型针对Ti-Zr-Nb 合金动态压缩强度的EMAP及R2，分别如图2 及图3 所示.

(4) 在实际注浆过程中，速凝类浆液在短时间内物质形态会发生相变过程，即采用的单一的非牛顿流体本构模型难以准确地描述这一复杂特征，后续有必要在该方面做进一步探讨。

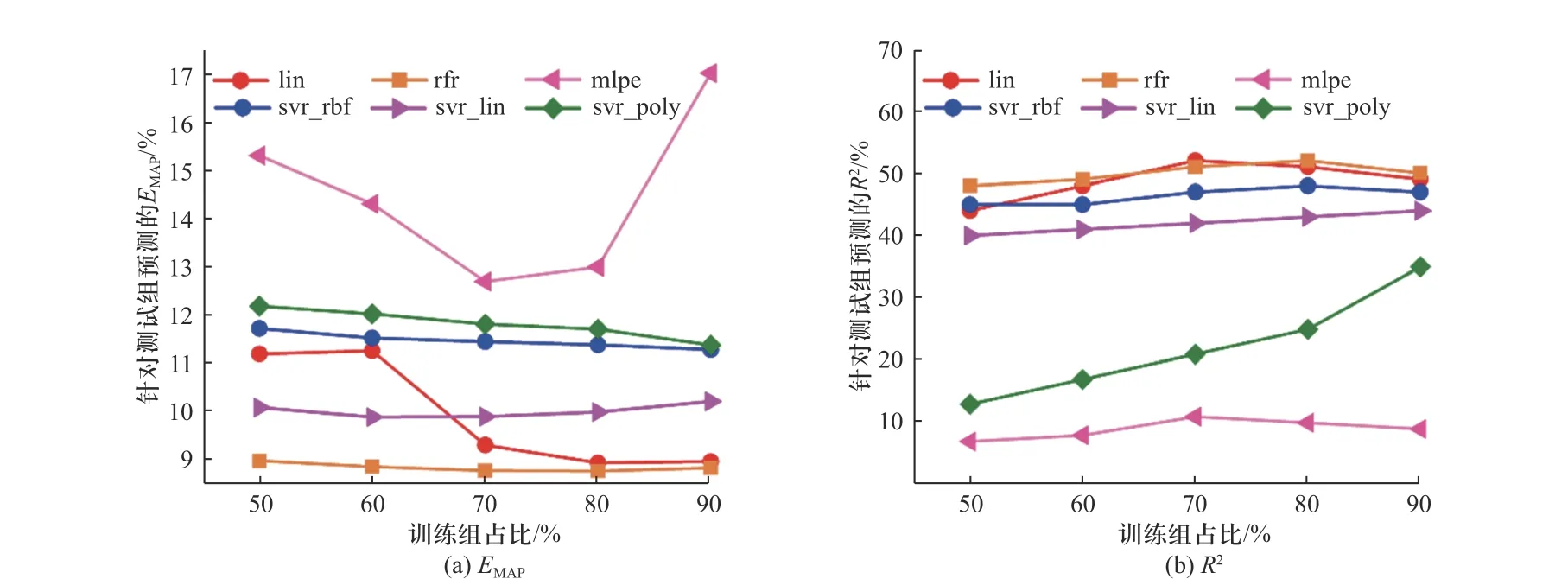
图2 各机器学习模型针对动态压缩强度预测时的测试集误差及拟合优度随训练集占比的变化情况Fig.2 The variation of test set error with proportion of training set in the prediction of dynamic compression strength by each machine learning model

图3 各机器学习模型在训练集占比80%时针对动态压缩强度预测的训练集及测试集的预测误差及拟合优度Fig.3 The prediction error of training set and testing set for dynamic compression strength prediction when the training set proportion of each machine learning model is 80%

如图2 所示为各机器学习模型针对动态压缩强度的测试组EMAP及R2随训练组占比的变化情况，由图2(a)可知，随机器学习训练组占比增加，各机器学习测试组误差均呈降低趋势(对于90%训练组误差升高趋势可认为是小样本量造成的机器学习模型过拟合现象).在图2(a)中，可以看到随机森林回归(rfr)模型具有最优的预测表现，且在训练集占比80%、测试集占比20%时，预测误差最低.由图2(b)可知，rfr及lin 在6 种模型中具有较高的拟合优度，但当样本量进一步降低时，lin 的表现要稍逊于rfr 模型.

为进一步评估各机器学习模型，计算了各机器学习模型在训练集占比为80%时针对Ti-Zr-Nb 合金动态压缩强度预测的EMAP及R2值，如图3 所示，其中，浅蓝色无斜线代表测试集误差，黄色有斜线代表训练集误差，若测试集误差与训练集误差相差较大，则说明该机器学习模型存在过拟合倾向，泛化能力较差.在机器学习模型的筛选过程中，基本原则是选择测试集误差小、拟合优度高且过拟合倾向低的机器学习模型.因此，由图3(a)、3(b)可知，在训练集占比80%、测试集占比20%的情况下，rfr 仍具有最小的预测误差、高的拟合优度以及较低的过拟合倾向.综上所述，本研究最终从构建的6 种机器学习模型中，优选出了适合小样本量数据集预测的随机森林回归模型(rfr)，开展Ti-Zr-Nb 合金动态压缩强度的预测研究，后续计算均采用训练集占比80%、测试集占比20%对初始数据集进行划分.

2.2 输入特征降维处理

经过机器学习模型筛选，基于Ti-Zr-Nb 合金动态压缩强度原始输入特征数据库，成功优选出了随机森林回归(rfr)模型，下一步便是针对此模型开展优化，即输入参量筛选及特征降维的过程.参量筛选是机器学习模型优化的关键步骤，其目的是从原始的输入特征集中获得最具代表性的子集，最终筛选出的特征集既包含了必要的信息，且冗余较少.此外，参量筛选也是降低机器学习过拟合倾向的关键步骤之一.

rfr 可通过自身算法，衡量输入参量对预测结果的贡献程度，并将其量化为数值输出.由此，针对动态压缩强度的预测，获得了初始特征的重要程度排序，如图4 所示，本文所采用的重要性数据均为随机森林回归模型重复计算200 次取平均值的结果.由图4 可知，对于动态压缩强度的预测，最为重要的参量为λ.在此基础上，本文采用两步参量筛选方法来识别影响Ti-Zr-Nb 合金动态压缩强度的主控参量，即皮尔逊相关系数+穷举法筛选.

图4 rfr 模型基于动态压缩强度预测的主控参量及其重要度排序Fig.4 The importance of the features computes by the rfr model based on the dynamic compression strength prediction.

2.2.1 皮尔逊相关系数法

一般情况下，任何两个特征参量之间都并非独立，而是具有一定的关联性.本文引入皮尔逊相关系数来表示特征参量两两之间相互关联的程度，皮尔逊相关系数的计算公式如式(4)所示

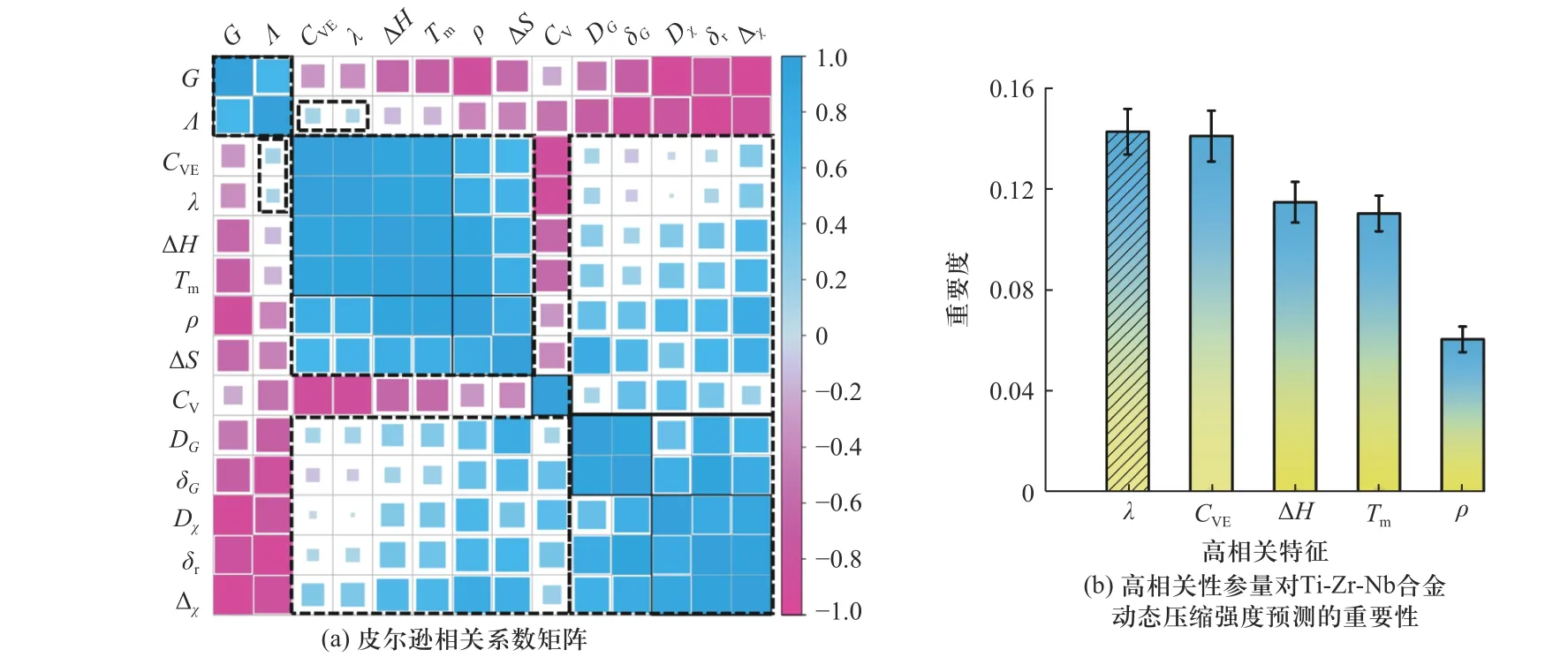
图5 基于皮尔逊相关系数的主控参量筛选Fig.5 The Pearson-correlation coefficient selection

在图5(a)中，蓝色代表两参量正相关，为图中用虚线圈出部分，粉色代表两参量负相关，图中正方形越大，则代表两参量之间相互关联的程度越高.本文将0.95 视为阈值，两参量之间的相关系数绝对值大于0.95 时，则两参量视为高度相互关联的参量，即机器学习预测中的冗余参量，仅需保留二者其中之一.根据皮尔逊相关系数的计算共获得了1 组包含5 个互相高度相关的参量，分别为：λ、CVE、ΔH、Tm、ρ，仅需保留其中一个.

结合图4 所示输入参量重要性，进行高度相关参量的筛选，筛选依据为去除针对预测结果的重要性相对较低的参量.图5(b)为5 个高度相关的参量针对Ti-Zr-Nb 合金动态压缩强度预测的重要性.由图5(b)，5 个参量的重要性排序为：λ>CVE>ΔH>Tm>ρ.因此，针对动态压缩强度的皮尔逊相关系数筛选，共去除了CVE、ΔH、Tm以及ρ4 个冗余参量，初始特征集中还剩余10 个参量，分别为λ、Δχ、CV、ΔS、Λ、DG、G、Dχ、δr、δG，剩余参量有待后续进一步筛选.

2.2.2 穷举法

经皮尔逊相关系数筛选，去除了具有高相关性的冗余参量.为进一步减少模型运算时间，提高预测精度，获得最优预测模型，采用穷举法针对动态压缩强度的预测对剩余的10 组输入特征做进一步筛选，即考虑剩余10 组输入特征从～的所有排列组合情况，并将这些组合依次作为输入参量输入至随机森林回归模型(rfr)中进行动态压缩强度的预测，最终依据误差分析，筛选出针对动态压缩强度预测的最优输入参量组合.在穷举筛选过程中，仍选择20%的数据作为测试集数据，选用EMAP作为误差分析指标，每组计算结果为重复计算200 次所得平均值.

图6 所示为针对Ti-Zr-Nb 合金动态压缩强度的的穷举法预测.以输入特征数目“3”为例，此时从10个参量中随机选取3 个参量作为输入参量，则存在种不同的输入参量组合，每个绿色空心球代表了不同的3 个输入参量对动态压缩强度的预测误差，而红色实心球则代表了当前组合对动态压缩强度的最小预测误差.从图6 中可以看出，随着输入特征数量的增加，机器学习的测试组误差呈现先降低后增加的趋势.这是因为随着输入特征的增加，完善了机器学习中有用的预测信息，进而增加了预测的可靠性；而过多的输入参量则会造成数据冗余，导致过拟合倾向，从而使预测误差升高.

图6 穷举法列举每种输入特征组合针对动态压缩强度的预测误差Fig.6 The test E MAP of each possible rfr model containing all subsets of the preselected 10 features

由图6 可知，针对Ti-Zr-Nb 合金动态压缩强度的预测，当输入特征数目为3 个时，机器学习模型的预测误差最低，分别为“Δχ、G、δG”，其中，Δχ和δG是影响位错运动的关键参数，一般来说，较高的失配能和弹性应变能可能导致位错运动的激活能较高，不利于位错运动.而参数δG代表模量失配，是影响晶格失配能和弹性应变能的重要因素；原子之间的化学相互作用和静电相互作用会对化学键的类型产生影响，进而决定了材料的物理和化学性质.其中，电负性差(Δχ)反映了元素之间的化学亲和力，常用于评价合金体系中各原子的得失电子能力.对于合金中的元素，电负性差越大，化学亲和性越强，形成的化学键越稳定.这可能会导致位错运动期间更多的能量消耗.在我们的前期研究中，上述两参数也是准静态压缩强度的主控参量；剪切模量G主要是影响合金抵抗剪切变形的能力，在多种强化模型中，G的大小决定了剪切应力的大小，因而剪切模量在Ti-Zr-Nb 固溶体合金动态压缩强度的影响参数中重要度较大.

此外，又计算了经参量筛选后的机器学习模型针对Ti-Zr-Nb 合金动态压缩强度预测的EMAP值，经模型优化后，预测误差降低至7.6%，较初始14 个输入特征时的预测误差8.7%相比有所降低，降幅为10%；拟合优度R2为65%，较优化前增加了13%.同时，在参量筛选过程中，机器学习模型中的冗余信息被剔除，提升了机器学习模型的运算速度及运算精度.优化后的机器学习模型针对Ti-Zr-Nb 合金动态压缩强度的预测效果如图7(a)所示.在此基础上，借助随机森林算法，得到了各主控参量的影响Ti-Zr-Nb 合金动态压缩强度的重要性及其排序，如图7(b)所示.针对Ti-Zr-Nb 合金动态压缩强度预测的主控参量排序为“Δχ>G>δG”，上述排序与14 组参数排序不同的原因可能是因为我们的样本量较小，初始输入特征的维数较大，因此在初始的构建的随机森林模型中存在一定的过拟合倾向，通过输入参数的降维这种过拟合倾向相应的降低.由此，完成了Ti-Zr-Nb 合金动态压缩强度的机器学习模型优化，优选出了影响Ti-Zr-Nb 合金动态压缩强度最重要的3 个主控参量及其重要度排序，成功地建立了一个数据驱动的材料设计策略，不仅揭示了Ti-Zr-Nb 合金的动态压缩强度的主要影响因素，也为其他固溶体合金的成分设计提供了指导作用.

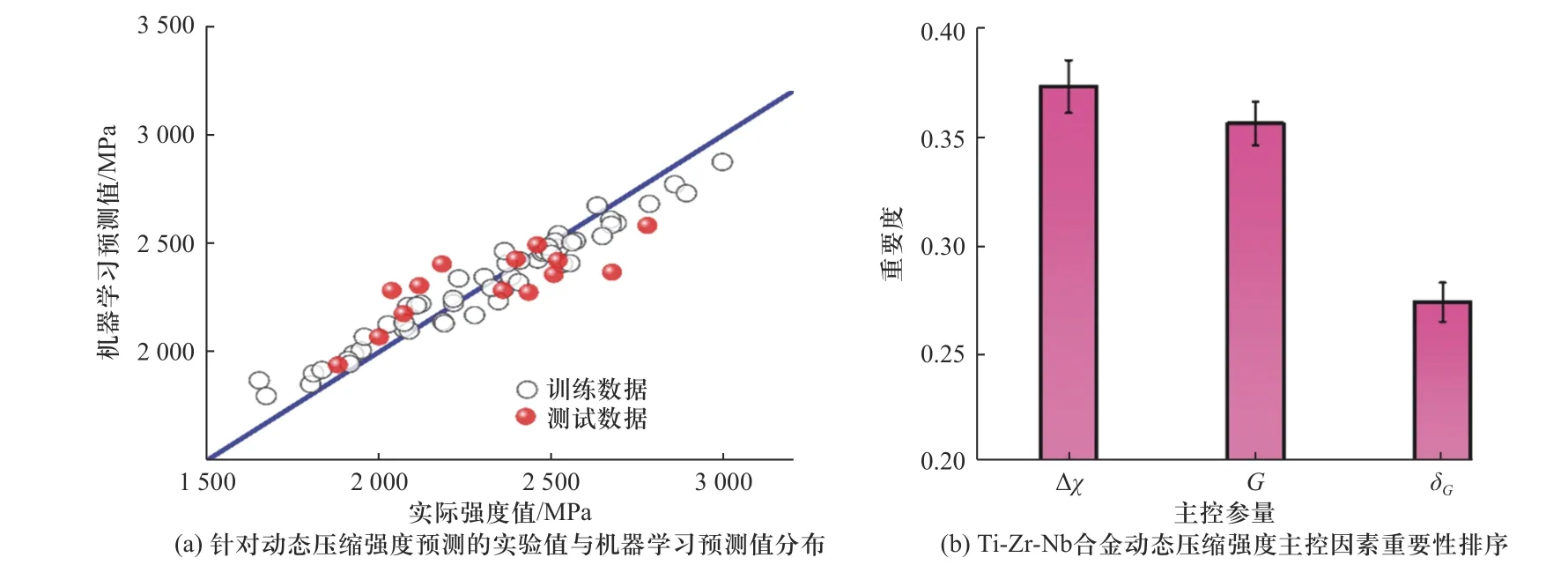
图7 最终模型预测结果及参数重要性排序Fig.7 Prediction of the optimal model and the order of importance

2.3 预测图谱建立与新合金设计

为进一步辅助成分设计，缩短材料制备周期，基于机器学习预测及所筛选的主控参量，构建了Ti-Zr-Nb 合金在不同加载应变率条件下主控参量与动态压缩强度的预测图谱，所选参数范围为Δχ：0.025～0.200，步长为0.025；G：20～60，步长为10；δG：0.05～0.20，步长为0.05，图谱如图8 所示.

由图8 可知，在相同的加载速率条件下，调整合金成分范围，使主控参量在“δG=0.05～0.10,G=35～42 GPa, Δχ=0.02～0.07”区间内，合金将具有较高的动态压缩强度，如图8 中红色虚线区域所示.根据图8所示的预测图谱，在上述参数范围内，开展了新合金的成分设计，成功设计了具有新成分的Ti-Zr-Nb 固溶体合金，成分为 “Ti：质量分数40%、Zr：质量分数10%、Nb：质量分数50%”，对应参量值分别为δG=0.098，G=39，Δχ=0.07.新合金在3 500 s-1的加载速率下动态压缩强度为3 100 MPa（3 次重复实验的平均值），其动态压缩曲线如图9 所示，与2 933 MPa 的预测值之间误差为6%，同时，所设计的新合金的动态压缩强度超出了数据库中现有合金的动态压缩强度.该设计思路不仅为Ti-Zr-Nb 系固溶体合金的快速设计提供了有效的理论支撑，也可推广至其他固溶体合金的动态压缩强度预测与成分设计中，为多元固溶体合金的精准成分设计与目标性能优化提供了崭新的方向.

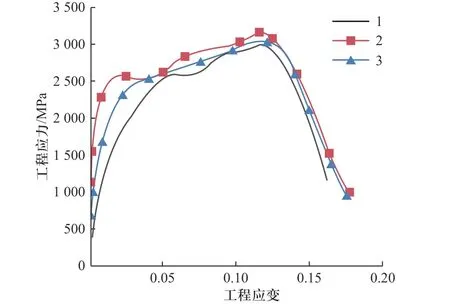
图9 新成分合金在3 500 s-1 应变率下的动态压缩曲线Fig.9 The dynamic compression strength of new alloys under 3 500 s-1 loading rate

3 结 论

①建立了包括数据库构建、模型选择、特征参量筛选、新合金预测在内的完整的固溶体合金成分设计和基础研究框架.根据机器学习模型筛选，优选出了适合小样本量数据学习的随机森林回归(rfr)模型，为Ti-Zr-Nb 固溶体合金的动态压缩强度预测提供了一种新的研究思路，也为其他小样本数据集的材料成分设计与性能预测提供了新的方法.

②通过机器学习模型优化与主控参量筛选研究，揭示了影响Ti-Zr-Nb 固溶体合金动态压缩强度的3 个关键主控参量及权重排序分别为：电负性差(Δχ)>剪切模量(G)>剪切模量差(δG)，经输入参数筛选优化后的机器学习模型预测误差<8%，为揭示多元固溶体合金动态力学性能的主要影响因素提供了指导作用.

③结合机器学习预测结果绘制了参量-性能预测图谱，结果表明在相同加载速率下，参量范围在δG=0.05～0.10,G=35～42 GPa, Δχ=0.02～0.07 区间内，合金具有较高的动态压缩强度，同时在上述参量区间内通过调控成分，成功预测出具有高动态压缩强度的新合金，其具体成分为 “Ti：质量分数40%、Zr：质量分数10%、Nb：质量分数50%”，动态压缩强度达到3 100 MPa，超出了数据库中原有的合金成分.本文所给出的预测图谱也可推广到其他固溶体合金动态压缩强度预测与成分设计中，为更高强度的固溶体合金的成分设计与性能优化提供了有力的理论指导与数据支撑.