基于BP神经网络的电磁阀多目标优化设计

2023-05-10沈丹峰郝祖茂李许锋

西安工程大学学报 2023年2期

沈丹峰,郝祖茂,赵刚,李许锋

(1.西安工程大学机电工程学院,陕西西安 710048;2.陕西长岭纺织机电科技有限公司,陕西宝鸡 721013)

0 引言

在喷气织机气流引纬过程中,纱线被主喷嘴的喷射气流牵引进入筘槽,再由辅助喷嘴喷射气流牵引穿过梭口。作为控制喷嘴开关的核心元件电磁阀则是纱线能否高效而稳定地穿越梭口的关键[1-3]。

衔铁所受到的电磁力和衔铁的质量共同决定电磁阀的动态响应特性,其中电磁力的影响为主。对于电磁阀,采用精准的理论模型计算电磁力非常不易。范玉等使用了磁路法建立了静态电磁力的数学模型,但只考虑了衔铁的磁阻,忽视了其他磁性材料磁阻对电磁力的影响,因此得到的结果不够精确[4]。文献[5-6]以磁导率作为电场-磁场耦合的桥梁,建立了电磁力的数学模型,经试验验证,误差在10%以内,虽然已经将所有磁性材料的磁阻考虑在内,但精度还是略显不足。文献[7-9]沿用磁路法建立了电磁力的数学模型,并结合有限元法对影响电磁力的因素,例如线圈的面积、位置以及衔铁的结构参数等进行了分析与讨论,得到了影响电磁力大小的基本规律并初步获取了电磁力的较优参数组合,但这种方法优化的速度过慢,易陷入局部最优解。文献[10-11]在上述方法的基础上,使用正交试验对有限元法得到的各结构参数组合进行了处理,获得了目标参数组合。虽然提升了电磁力优化的速度,但是所得出的结果并未能超出选取水平的范围,具有一定的局限性。桂肃尧等使用多目标优化遗传算法对建立好的衔铁运动数学模型进行优化,获得了最佳参数组合[12]。多目标优化遗传算法较于正交试验设计试验次数多,处理参数的交互性效率更高,得到的优化结果更加精确,但因为电磁阀内部物理场的复杂性,数学模型无法精确建立,因此使用NSGA-II优化数学模型后的结果也会产生较大误差。文献[13-16]通过有限元法结合最优拉丁方试验设计建立了电磁阀结构参数与电磁力的Kriging近似模型,并通过NSGA-II对其进行了优化。但近似模型的建立必须人为地选取适当的函数形式,然而,非常恰当的函数形式不易选取。而具有多维函数映射能力的BP神经网络不需要确定数学方程,只需给出输入值与其对应的期望值,通过自身训练便可以完成对目标值的预测。

因此,为了更加准确地提升衔铁受到的电磁力,本文以SMC公司的AVJ3220-X235电磁阀为研究对象,建立并验证了三维有限元模型,以衔铁结构为设计变量,将有限元仿真计算得到的电磁力作为输入变量,建立了BP神经网络预测模型,同时考虑到衔铁结构参数对质量的影响也会影响电磁阀的动态响应特性,最终选取了电磁力和衔铁质量这2个目标对象,采用多目标优化遗传算法对其进行优化,以求得最佳参数组合。

1 电磁阀有限元模型的建立与验证

1.1 电磁阀基本结构

AVJ3220-X235电磁阀是一种纺织专用电磁阀,具有外漏堵绝、内漏易控和快速响应等特点。电磁阀的整体结构由衔铁、复位弹簧、套筒、铁芯和线圈等组成,如图1所示。

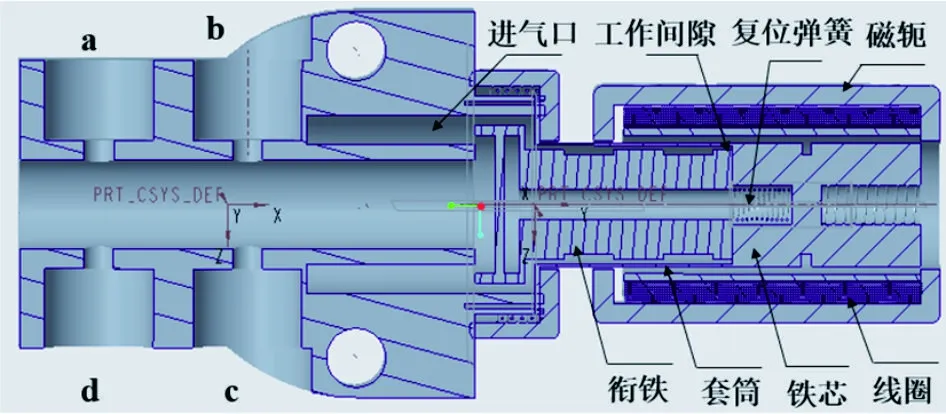
图1 电磁阀结构的剖面

电磁阀可以连接4个辅助喷嘴,分别为阀座的a、b、c、d等4个通道。当线圈接入电流,铁芯被磁化吸附衔铁,阀腔与外界连通,气流从辅助喷嘴喷射而出,牵引纱线穿越梭口。当线圈断电后,衔铁所受到的电磁力消失,衔铁在复位弹簧的作用下回到原来位置,阀腔与外界隔绝,喷嘴停止工作,完成纱线的牵引工作。

1.2 模型的建立

1) 电路模型。由基尔霍夫定律可得电流与电压之间的关系为

(1)

式中:U为线圈两端电压;R为线圈电阻;N为线圈匝数;i为线圈电流;Φ为总磁通量。

2) 磁路模型。根据电磁阀的结构简图,可求得磁路总磁阻为

Rtot=RX+Rj+Rt+Rδ+Rce

(2)

模型中,磁阻和总磁通存在着下列关系,即

ΦRtot=Ni

(3)

式中:Rtot为电磁阀的总磁阻;Φ为总磁通量;RX为衔铁磁阻;Rj为铁芯磁阻;Rt为套筒磁阻;Rδ为工作间隙磁阻;Rce为磁轭磁阻。磁阻计算公式为

(4)

式中:Rm为磁路磁阻;L为磁路长度,m;S为磁路横截面积,m2;μ0为空气磁导率,H/m。

3) 电磁力计算。电磁力由虚拟功原理根据三维静磁场中的麦克斯韦的求解方程[17]计算得到,即

(5)

在优化过程中,衔铁的磁阻总是随着结构的变化而变化,难以通过理论模型计算出准确的电磁力,因此采用有限元法获取电磁力。

1.3 电磁力有限元模型求解

电磁阀主要结构单元由衔铁、套筒、磁轭、线圈组成。通过CREO5.0软件建立3D模型并导入Maxwell 16.0中。在模型的建立过程中,考虑到电磁阀的工作特性和减少模型的计算时间,以及为了简化分析衔铁所受到的电磁吸力,所建立的电磁阀模型舍弃了垫片和弹簧等一些非磁性材料的结构部分,并根据实际电磁阀的工作原理,由以上4种结构在Ansys Maxwell 16.0中建立了如图2所示电磁力的3D有限元求解模型,其中红色线框表示的是整个有限元模型求解域的边界。

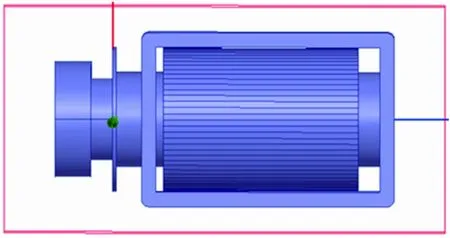
图2 电磁力有限元仿真模型

衔铁的材料是磁导率和饱和磁感应高的DT4C,密度为7.860 g/cm3。铁芯、套筒和磁轭的材料是具有高磁导率且同时具有高电阻率的硅钢片。线圈的材料为铜。此外,安匝数为1 742,衔铁与铁芯之间的距离即工作间隙设置为2 mm,采取自适应网格剖分用以求解电磁力。

1.4 模型的实验验证

图3所示为电磁力的测试平台。CZLYB-3力传感器的一端固定在工作台上,另一端与衔铁相连,可在水平方向进行移动,用以调整衔铁与静铁芯之间的距离即工作间隙。上位机对下位机发送指令,并为电磁线圈提供电流,线圈通电铁芯被磁化产生电磁力吸引衔铁,力传感器产生微弱的电压信号,捕捉到的信号经放大器处理后即为所测得的电磁力大小。通过改变驱动电流和工作间隙的值,实现对电磁力的测量。

图3 电磁力测试台

为了验证电磁力有限元模型的可行性,选取了工作间隙2 mm,驱动电流0.1～1.5 A,共15组实验与有限元模型仿真进行对比,结果如图4所示。

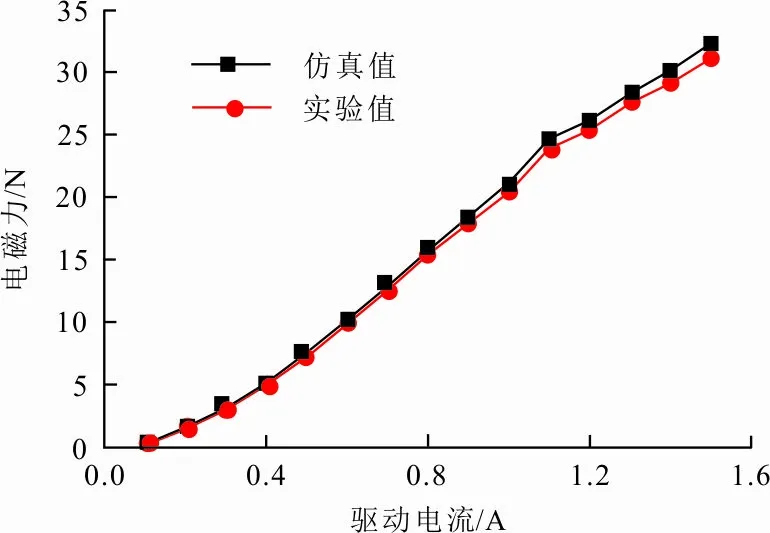
图4 模型的实验验证

从图4可知,随着驱动电流增加,仿真与实验值的误差也在不断增加。这是由于仿真设置下的材料处于理想状态,并未考虑高温等对材料磁导率的影响,电流越大,这种影响越大直至达到磁饱和。但误差出现的最大值小于5%,且总体趋势趋于一致,因此验证了有限元模型的可行性。

2 BP神经网络模型的搭建

虽然建立的电磁力有限元模型能够匹配实际物理阀体,然而建立的有限元模型并不能对阀体结构进行优化。为了优化电磁阀结构,获取更好的电磁响应,采用BP神经网络进行模型预测。

2.1 BP神经网络训练集数据的获取

衔铁的结构尺寸在很大程度上影响着自身所受到的电磁力和质量,进而影响着电磁阀的动态响应特性。图5为AVJ3220-X235电磁阀的衔铁结构简图,衔铁各部分结构尺寸依次为:H1=2 mm,H2=H3=H4=5 mm,H5=5 mm,H6=3 mm,H7=21 mm,D1=11 mm,D2=10 mm,D3=3 mm,D4=14 mm,D5=16 mm。

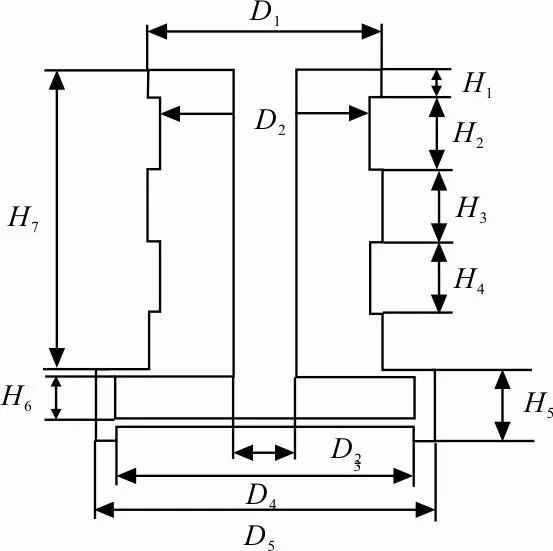
图5 衔铁结构简图

由磁阻计算公式可知:衔铁与铁芯的接触面积越大,磁路中的磁阻越小;衔铁的长度越短,磁路中的磁阻越小,受到的电磁力越大,反之越小。因此衔铁直径D1、内径D2和接入磁路长度H1、H2对电磁力的影响最大。

综上所述,选取了D1、D2、H1、H2这4个结构参数作为优化电磁阀性能的决策变量,并根据实际尺寸空间对每个决策变量取4个水平,如表1所示。

表1 决策变量组合

2.2 BP神经网络预测模型的建立

BP神经网络算法可以根据样本特性调整结构参数,具有较强的适应力;并且可以对输入参数的准确性进行判断与处理,具有良好的稳定性和容错性[18]。选取上述4个决策变量作为BP神经网络预测模型的输入变量,选取衔铁所受到的电磁吸力作为输出变量,建立了BP神经网络的电磁力预测模型。为避免神经元的饱和,对输入量和输出量进行归一化处理,转化为[-1,1]区间的数值。在已获取的256组训练样本中,随机选择其中的226组数据用来训练神经元,剩余的30组数据用以测试。选取的输入量有4个,输出量有1个,因此可以确定输入层和输出层的节点数量分别为4和1。隐藏层节点数量可根据经验公式(6)进行计算,即

(6)

式中:N1、N2分别为输入层节点数和输出层节点数;N为隐藏层节点数;ε为0～10的常数[19-20]。

综上所述,在ε取值范围内,通过改变隐藏层层数,选取了最小均方根误差对应的节点数目10作为隐藏层层数,构建了4-10-1的BP神经网络结构。

2.3 BP神经网络预测模型的验证

电磁力BP神经网络预测模型建立完成后,需对训练完成的模型进行预测。图6为256组有限元模型仿真数据中随机抽取的30组实际值与预测值的对比。

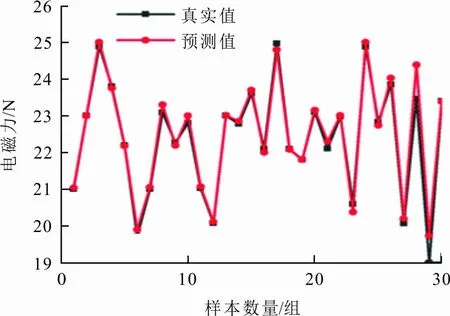
图6 预测值与真实值对比

可以看出,预测值与实际值的曲线走向趋势基本一致,并且预测值与实际值出现的最大误差为3.28%,符合BP神经网络对精确度的要求[21],能够实现精准预测。最后,将预测好的模型进行保存,作为后续优化模型使用[22-23]。

3 多目标遗传算法优化

3.1 优化目标

选取2个优化目标,一是衔铁处于工作间隙2mm位置时受到的静态电磁力,二是衔铁质量。电磁力的数学模型可由2.3节得到的BP神经网络预测模型代替,衔铁质量的数学模型由质量计算公式求得,即

(7)

式中:m为衔铁的质量,g,ρ为电工纯铁的质量密度,g/cm3,V为衔铁的体积,cm3。

在同一个系统中,所选取的4个决策变量之间存在不同的组合形式,通过计算可以得到相应的电磁力和衔铁质量。电磁力和衔铁质量都在不同程度上影响着电磁阀的动态响应特性。强大的电磁力可以将衔铁快速地吸向铁芯,能够大幅度缩小电磁阀开启的时间。衔铁的质量越轻,衔铁在上升的过程中受到重力越小,衔铁与铁芯吸合的时间也会缩减。但矛盾点在于,衔铁结构的改变必然会给电磁力和衔铁质量同时带来影响。为了在不增加衔铁质量的前提下尽可能地提高电磁力,所研究的问题便可以转换为求解电磁力的最大值和衔铁质量的最小值,目标函数为

(8)

3.2 多目标优化过程

采取的优化算法为多目标优化遗传算法[24-26],与GA不同的是,NSGA-II是一种可以对多目标同时进行搜索最优解的优化方法,因此得到的解并不是单一解,而是一组最优解集。使用NSGA-II优化电磁力和衔铁质量的流程如下。

1) 对选取的4个结构参数D1、D2、H1、H2在取值范围内随机生成初始种群,并分配适应度。

2) 以适应度为选取参考,每次随机从父代种群中选择2个个体进行锦标赛,选择适应度高的个体进入交配池。

3) 从池中随机选择2个父代进行交配,根据交叉概率,将他们的染色体按照模拟二进制交叉的方式进行处理,生成2个新的个体。

4) 对于新个体的染色体,根据变异概率,采用以个体为中心均匀变异的方式进行变异处理。

5) 由D1、D2、H1、H24个结构参数求出衔铁受到的电磁力和其本身的质量作为目标函数。

6) 根据多目标进化算法的适应度分配规则,为每个个体分配相应的适应度。

7) 新种群生成。

8) 若当前进化代数已经达到了设定的进化代数,则终止程序;反之,跳转到第3步。

3.3 优化的结果与讨论

使用多目标优化遗传算法完成了基于BP神经网络预测模型的多目标优化。其中,设定的种群数量为50,交叉概率为0.8,变异概率为0.4,迭代次数为100。得到的Pareto曲线如图7所示。

图7 Pareto最优解

结果显示,衔铁质量和电磁力的关系可以分成2段,一段趋势较缓另一段趋势较急,但都呈线性相关,电磁力随着衔铁质量的增加而增加。理想状态下,电磁力越大对于电磁阀的开启过程越有帮助。但在实际工况条件下,电磁力的大小又受到很多条件的制约,衔铁的质量便是其中一个,因此需要在二者之间进行权衡,但因为优化结果得到的Pareto解集曲线呈线性关系,无法直接获取衔铁质量的最小值。因此,在以不增加衔铁质量的前提下,从非劣解集中选取了与优化前衔铁质量最相近的参数组合作为最优解进行讨论,将满足要求的参数组合重新代入到已建立好的三维有限元模型中,驱动电流设置为1A,计算优化后的电磁力和衔铁质量,优化前和优化后的结果如表2所示。

表2 优化前后结果的对比

从表2可知,优化后的衔铁质量相对于优化前减轻了1%,而电磁力较于优化前增加了11.5%。为了进一步研究衔铁结构参数在不同工作间隙下对电磁力的影响,从厂家定制了优化后的衔铁。在驱动电流为1A,其他条件不变的情况下,通过有限元模型计算和实验得到如图8所示的结果,工作间隙的取值分别为2.0、1.5、1.0、0.5mm。