基于Hough-Harris 的消音壁顶点检测
2023-05-10李国旺李英马韵琪夏晨旭
李国旺,李英,马韵琪,夏晨旭
(长春理工大学 光电工程学院,长春 130022)
消音壁领域中顶点检测是关键任务之一,其顶点在图像处理中可认为是角点,而角点一般定义为两条边的交点,是图像中重要的结构信息之一,在图像处理领域中有着关键性作用。目前对角点定义的数学公式不具有普遍性,根据不同领域内针对检测的角点需求不同,其表达方式也不一样,例如图像亮度变化剧烈的点和图像边缘曲线的曲率局部极大值点等。目前角点检测的方法主要分为两种:基于灰度强度变化检测和基于边缘轮廓检测[1]。由于基于灰度强度变化的检测算法简单、实时和稳定性高,因此被广泛应用。
基于灰度强度变化的角点检测主要通过图像局部灰度值的变化判断角点。在1977 年,Moravec[2]提出Moravec 角点检测,在图像上通过二值矩形窗口滑动寻找最小灰度值变化的最大值;1988年受Moravec思想启发,Harris和Stephens[3]提出Harris 角点检测,利用自相关矩阵求出特征值,来确 定 响 应 函数;1997 年Smith 和Brady[4]提出SUSAN(Smallest Univalue Segment Assimilating Nucleus)角点检测,利用像素领域的圆形模板,判断此点是否属于USAN 区域,进而判断是否为角点;1998 年Trajkovic 和Hedley[5]提 出FAST 角点检测,观察某点领域内经过该点的任意直线上的灰度变化情况,计算出水平和垂直方向灰度变化值,构建角点度量函数判断是否为角点。近年来,国内外科研人员也基于上述方法作出了一些改进,例如:2006 年Rosten 和Drummond[6]提出了高速角点检测算子,利用机器学习加速角点检测;2012 年Bongjoep 等人[7]利用自适应于图像的结构张量检测角点,提高Harris 算法的检测准确率;2013 年He 等人[8]在SUSAN 算法的基础上,提出角点预检测减少伪角点,减少计算量;2014 年Qiao 等人[9]提出了一种改进的Harris亚像素点检测算法,提高了对含有噪声图像角点检测的准确性;2017 年卢伟家等人[10]提出在Harris 算法中加入一种加权系数自适应的均值滤波,提高精确度和检测速度的同时减少伪角点的检测;2016 年王冠群等人[11]提出一种基于高斯变换的多尺度SUSAN 角点检测方法,解决了传统SUSAN 算法在单一尺度下检测角点的缺陷;2017 年Wang 等 人[12]针 对Harris 算 法 选 取 合适阈值的问题,提出一种迭代阈值的自适应Harris 角点检测方法;2017 年刘妍等人[13]提出一种基于SAR-FAST 角点检测算法,以检测点为圆心,选择合适半径,根据圆周上进行滑动窗口检测,检测出的角点稳定性和重复性好;2020 年周伟等人[14]提出一种改进的Harris 角点检测,结合多边形逼近方法提取目标轮廓拐角顶点;2021年 苗 荣 慧 等 人[15]利 用Harris 算 法 和RANSAC 去除误匹配点,实现图像精准匹配。
综上所述,对图像检测角点的方法众多,都是对其检测角点坐标准确率、精准性、去伪角点或适应性进行改进。但是,这些方法大多数适应自身领域,对其他领域并没有较好的普遍适应性,目前消音壁毁伤评估还处于人工评估阶段,并没有对其顶点检测的方法。由于毁伤后造成消音壁边缘产生畸变,上述方法并不适用消音壁的顶点检测。因此,本文提出一种基于Hough-Harris 的消音壁顶点检测方法。首先,对图像进行霍夫直线检测,以拟合直线后得到的角点作为基点;然后,再通过Harris 算法检测出消音壁边缘上存在的角点;最后,利用基点以及基点步长为10 领域内的角点构建回归方程,采用基于高斯的最小二乘法求出最小误差,进行消音壁顶点预测。将Hough 算法、Harris 算法检测出的角点以及本文算法预测出的角点与真实角点进行对比分析,计算坐标偏差,同时计算IoU(Intersection over Union)指标,验证本文提出的算法检测角点更符合真实角点,能提高角点检测准确性,减少后续毁伤评估、三维重建等工作任务中计算的误差。
1 消音壁顶点检测
无人机拍摄消音壁获取图像时,因为拍摄时会产生抖动,获取的图像也并不是一副单独消音壁块,周围还有其他部分消音壁块。消音壁后续的毁伤评估不是对整体结构进行打包式评估,而是对具体的毁伤部分进行局部毁伤评估。因此,需要对图像进行顶点检测,通过检测出的顶点进行几何校正,将消音壁块从图像中分离出来。
1.1 霍夫直线检测
霍夫变换(Hough Transform)由Hough[16]于1962年首次提出,1972 年Duda 和Hart[17]将 此 方法推广使用。到目前为止,霍夫变换是图像检测几何形状的基本方法之一,其变换思想是两个不同坐标空间之间的相互转化,将一个空间中相同的曲线或直线一一映射到另一个空间的一个点上形成峰值。霍夫直线检测(Hough Line Detection)具有连接不连续线段的特点,可以用于消音壁块的边框检测,坐标转换过程如图1 所示。
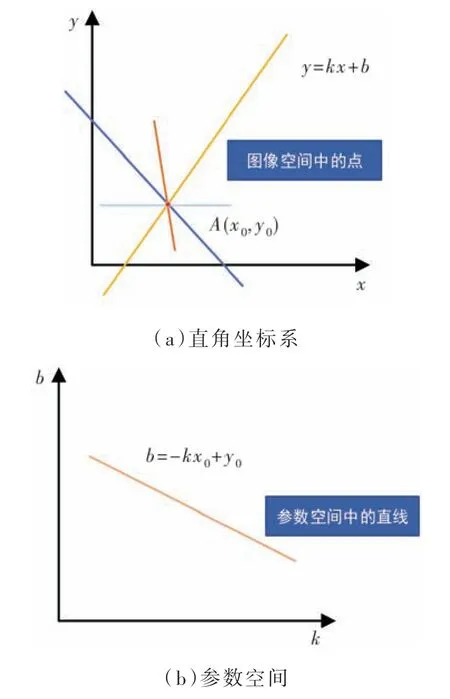
图1 坐标转换过程
其中,直角坐标系中的直线表示为:
式中,k是直线的斜率;b是直线的偏置。而直角坐标系中点A的坐标为(x0,y0),经过点A的直线有无数条,这些经过该点的直线称为一簇直线,该簇直线表示为:
因为x0和y0为固定值,不同取值的k和b代表经过点(x0,y0)的不同直线,可以将方程变换为:
此时,可以将x-y空间中过点A(x0,y0)的一簇直线转换为参数空间k-b中的一条直线。同理,再在x-y空间内增加点B(x1,y1),映射为参数空间中另一条直线,两条直线的交点反映射到x-y空间中为经过A和B的一条直线,如图2 所示。

图2 多参数转换图
由此看出,经过上述转换后,直角坐标系中x和y变为参数空间中斜率和偏置,此时的直线也转换为过点(b0,k0)的直线簇。但是当直角坐标系x-y中的直线垂直于x轴,其参数k为无穷大,参数空间将不能表示直角坐标系x-y中的直线。因此,将直角坐标系x-y转换为极坐标系,此时包含表示直线的所有范围,极坐标形式如式(4)所示:
其中,r为原点到直线的距离;θ为原点到直线垂直距离的交点与横轴的夹角。此时图像空间上的每一个点对应极坐标系上的一条正弦曲线。直角坐标系转换到极坐标的过程如图3 所示。
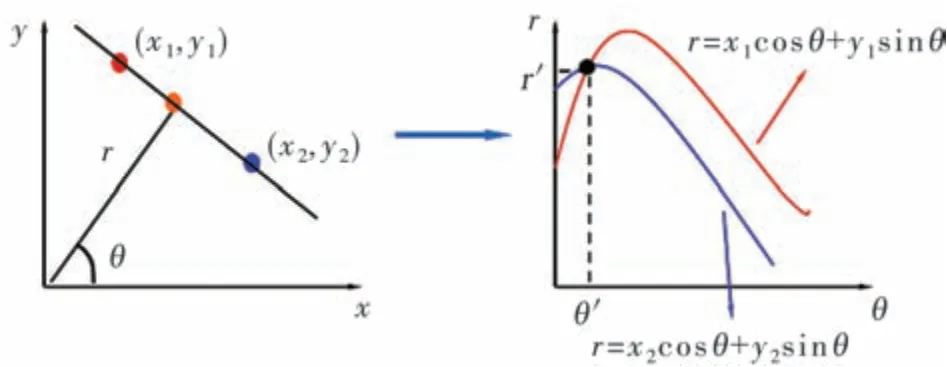
图3 转换过程
霍夫直线检测就将图像中的直线转换到参数空间(极坐标系)中的点,通过参数空间中曲线的交点反过来求出图像空间的直线。将图像灰度化后进行Canny 边缘检测和形态学处理,由于消音壁边框产生了畸变,利用霍夫直线检测边框为一些连续线段,检测线段映射到原图上的结果如图4 所示,其中图4(a)和图4(b)为消音壁样图。

图4 霍夫直线检测消音壁
检测出消音壁四周边框上的线段后,由于线段仅为部分边框且不连续,需要对边框上的线段进行直线拟合,将拟合后的直线两两相交的交点作为消音壁顶点,交点坐标映射到原图的结果如图5 所示。

图5 拟合直线后的角点
1.2 Harris 角点检测
Harris 角点检测算法的思想即用一个滑动窗口在图像上进行滑动时,会产生三种情况,在平坦区域、在边缘区域和在角点区域,如图6 所示。在平坦区域滑动时,窗口内灰度值变化相对平缓;在边缘区域滑动时,窗口内灰度值会沿某一方向(X轴或者Y轴)产生相对较大的波动;窗口在角点区域滑动时,X轴和Y轴方向都会产生较大波动。
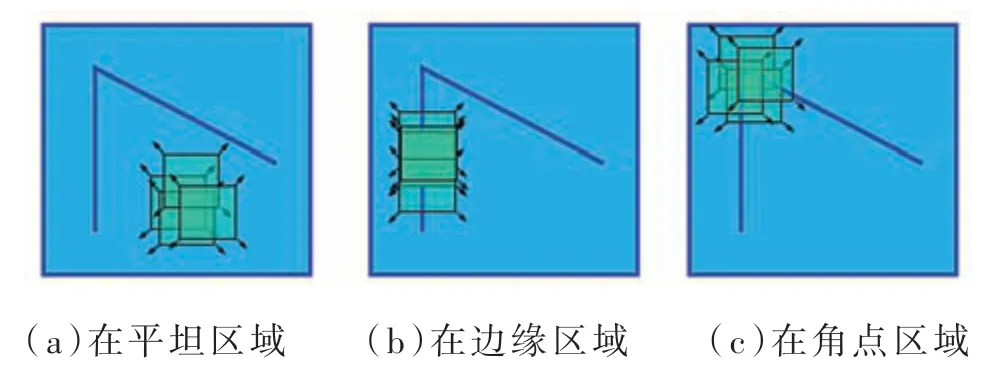
图6 窗口在不同区域上的移动
滑动窗口在图像上平移后产生灰度变化的相关性用SSD(Sum of Squared Difference)计算,SSD 越大,相关性越差,中心点越有可能为角点,其数学表达式为:
其中,u和v为窗口偏移量;x和y为窗口内像素坐标位置;I(x,y)为在(x,y)坐标下的像素值。对I(x+u,y+v)进行一阶泰勒展开为:
代入式(5)中,由于局部移动量[u,v]较小,变化矩阵形式近似为:
其中,自相关矩阵M表达式为:
通过自相关矩阵M可以求出该矩阵特征值λ1和λ2,利用这两个特征值确定角点检测响应函数R为:
式中,k为错误角点响应抑制常数,取值范围一般为0.04~0.06。本文Harris 角点检测采用核大小为5 × 5 的滑动窗口进行检测特征值λ1和λ2,计算出角点响应函数R来判断该点是否是角点,检测出消音壁的角点结果如图7 所示。

图7 Harris 检测的角点
1.3 Hough-Harris 角点检测
霍夫直线检测消音壁,能快速定位消音壁四周边缘直线,拟合直线后求得的四个交点为消音壁大致的四个顶点。但是,由于消音壁经过毁伤后四周边框产生了畸变,霍夫直线检测的直线并不能准确地表达消音壁四周边缘,而产生畸变后的边缘也不能被一条直线完整的检测到,本文霍夫直线检测后拟合的直线是通过消音壁与消音壁之间的距离产生的缝隙,扩大了直线检测的范围,所以,通过霍夫直线检测出的角点进行透射变换后,消音壁图像四周存在大量缝隙,较为严重的影响后续对消音壁毁伤评估等操作。Harris 算法能相对准确地检测出消音壁四个顶点,能有效避免大量缝隙并行透射到消音壁图中,但是,检测出的角点中存在大量伪角点,这些伪角点并不是需要的,而且计算机也无法自主判断。
综上所述,霍夫直线检测和Harris 角点检测针对消音壁顶点检测时,不能满足精度和准确需求。因此,本文提出了一种Hough-Harris 角点检测方法,以霍夫直线检测的交点PL为基点,Harris 检测的角点PH为自变量,建立回归模型,构建回归方程,基于高斯提出的最小二乘法求参数,其PL与PH关系表达式为:
其中,Py为PH与PL纵坐标差值;Px为PH与PL横坐标差值;β0为偏置;β1为斜率;ε为Px与Py之间的线性关系外的随机因素,即误差项。回归方程表达式为:
对于每个角点PH:
由于误差服从高斯分布,则:
将式(12)代入式(13)可得:
则似然函数为:
对似然函数取对数后:
化简后,求出最佳公式为:
将式(17)代入回归方程(11)中,求偏导后求解可得:
获取回归方程后,以霍夫直线检测的交点为原点,相邻的两个交点方向为坐标方向,构建参数空间,原点到对角交点的方向为预测真实角点的方向。为方便计算,将参数空间映射到直角坐标系中,与回归方程的交汇处为预测的角点。回归方程的计算选取距离原点步长不超过10 个像素点的Harris 检测出的角点,而且在参数空间一、三象限内的角点。
2 实验结果分析
本文实验硬件环境为:Intel Core i7-7700H CPU;内存为16 GB;64 位Windows10 操作系统。软件实施平台为Visual Studio 2019,消音壁部分全景图如图8 所示。

图8 消音壁部分全景图
选取图4 验证本文Hough-Harris 角点检测算法性能,其中,图4(a)和图4(b)为消音壁样图,图5(a)和图5(b)为霍夫直线检测的角点图,图7(a)和图7(b)为Harris 角点检测图,分别求出Hough、Harris 和Hough-Harris 算法检测出的角点坐标,与真实值进行对比。结果如表1、表2 所示。

表1 样图一检测角点坐标(单位:像素)

表2 样图二检测角点坐标(单位:像素)
根据表1 和表2 可知,图像中Harris 检测出的角点个数根据响应函数选取的阈值T变化而不同:阈值T越小,角点响应越强烈,获取的角点也越多;阈值T越大,角点响应越微弱,检测出的角点也越少。阈值T大小的选取影响角点检测个数,同时,也影响计算机运算时间,每个角点响应都需要计算,阈值选取过小时,会产生大量伪角点,大量增加了计算机运算负荷。因此,本文选取阈值T为85,在能检测出角点的同时,减少伪角点的出现,提高计算机计算性能。样图二的Harris 检测出的角点较多,本文仅选取离基点欧氏距离最近的前8 个角点进行验证。霍夫直线检测角点、Harris 检测角点和本文算法检测角点与真实角点偏差对比分析,本文算法检测的角点普遍靠近原点,结果如图9 所示。
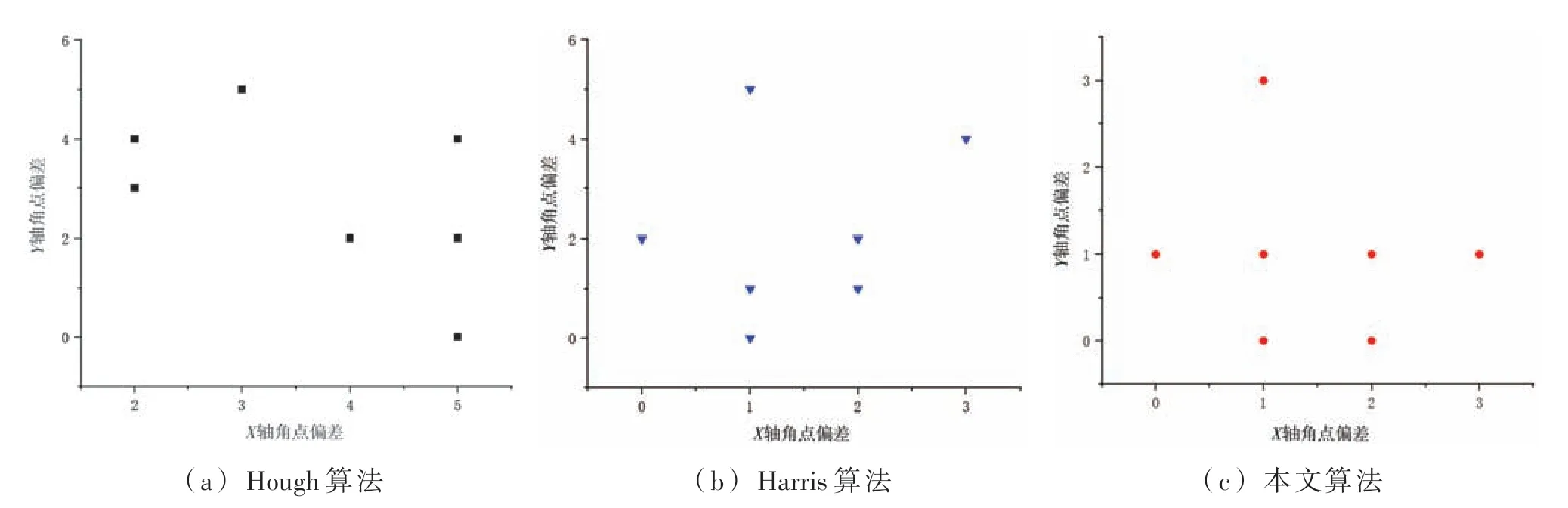
图9 角点偏差分析
从表3 可以看出,Hough 算法的PLx和PLy偏差最大,本文算法的PLHx和PLHy偏差最小。然后,利用各种算法检测出的角点,计算四边形面积,通过IoU 计算评估算法,IoU 计算的是“预测的边框”和“真实的边框”的交叠率,即他们的交集和并集的比值。理想情况下比值为1,即完全重叠。IoU 计算过程如图10 所示,计算结果如表3所示。
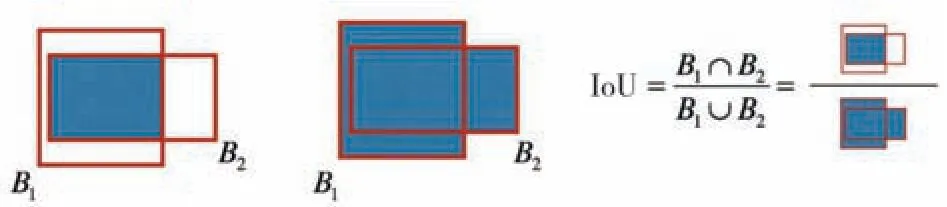
图10 IoU 原理

表3 IoU 结果对比分析
由表3 可知,样图一和样图二通过Hough 算法检测角点形成面积的IoU 为93.37%和96.02%;通过Harris 算法检测角点形成面积的IoU 为95.82%和96.51%;而本文算法检测形成的IoU 能达到98.13%和98.71%。本文算法检测的IoU 比Hough 算法和Harris 算法检测的IoU 分别高4.76%、2.69% 和2.31%、2.20%。因此,本文算法检测消音壁角点更接近真实值,透射变换后图像如图11 所示。

图11 校正后的消音壁
3 结论
为了更精确地检测出消音壁四个顶点,本文提出一种基于Hough-Harris 的消音壁顶点检测算法。本文算法以Hough 算法检测的角点为基点,以基点自身步长在10 以内Harris 算法检测的角点为样本点,构建回归方程,基于高斯提出的最小二乘法求解最小误差,能有效去除Harris 算法检测的伪角点,预测出消音壁四个顶点坐标。实验结果表明,本文算法预测顶点坐标与真实顶点坐标偏差量都小于Hough 算法和Harris 算法检测出的角点;本文算法的IoU 评估指标高达98%以上,高于Hough 算法和Harris 算法的IoU 指标。因此,本文算法能较精确地检测出消音壁顶点的同时,也有助于提高后续对消音壁毁伤评估、三维重建等工作任务的精度。
