改进的Sobel 算子图像清晰度评价算法

张永超，李英，唐智勇，谢康旗

（长春理工大学 光电工程学院，长春 130022）

随着现代自动化控制技术、微电子以及数字图像处理等技术的快速发展，自动聚焦技术已经被广泛地应用于照相机、显微镜、内窥镜和摄像机等光电成像设备中。目前显微镜自动对焦方法主要分为主动式对焦与被动式对焦[1]。主动式对焦通过测量镜头与被测物之间的距离，然后移动切片到焦点处以达到对焦的目的；被动式对焦主要通过图像处理技术，通过采集一系列图像进行分析判断离焦程度来实现对焦。由于基于图像处理技术的被动式对焦方法具有低功耗、低成本、高度集成化和智能化等优点，被广泛运用于光电对焦设备中。

以数字图像处理为基础的自动对焦方法中，图像清晰度评价函数是决定整个自动对焦系统准确度和速度的关键。图像的清晰度值是可以反映对焦系统的离焦程度的，图像清晰度值越大，图像越清晰，边缘细节多，说明处于近焦区域；图像清晰度值越小，图像越模糊，说明处于离焦区域；在空域上表现为相邻像素点的灰度值变化较大，在频域上表现为高频分量较多。空间域函数计算简单，稳定性好，频域函数复杂计算量大。近年来人们对空域类梯度评价算法进行了一系列研究，以典型的边缘检测算子为例，如Sobel、Kirsch、Laplace 等为基础对图像清晰度函数进行改进，以提升评价算法性能，其中Sobel 算子耗时短，操作简单。2017 年褚翔等人[2]提出了一种基于8方向Sobel 算子边缘加权的调焦评价函数，提升了边缘检测准确度，但运算量大。2018 年许乐灵等人[3]提出了一种引导滤波自适应双阈值并改进Kirsch 算子的优化边缘检测算法。2020 年王灿芳等人[4]提出了一种结合了Variance 函数与Brenner 函数优点的新的图像清晰度评价算法。2020 年郑欢欢等人[5]提出了基于均值计算和差分处理角度构造了5×5 的梯度权值模板的改进的Sobel 算子的边缘检测算法。2022 年邹雨彤等人[6]结合人类视觉系统（HVS），提出了采用灵活性阈值的多方向权重Sobel 算子的改进图像清晰度评价方法。2022 年李雪梅等人[7]提出了将加权核范数最小化（WNNM）图像去噪算法与Sobel 边缘检测算法相结合的边缘检测算法，提升了算法的抗噪性。

通过以上文献可知，对基于边缘检测算子的图像清晰度函数的改进方法主要包括改进梯度模板、给梯度模板加权、改进图像边缘提取的阈值、结合其他算法等。但大多数算法较为复杂，运算量大，对硬件要求较高，因此需要对传统梯度函数进行改进，使评价算法既简单又具有强的抗噪性。空域类梯度评价函数中Sobel 算子虽然可以滤除部分噪声，但是仍然对噪声较为敏感，而且存在方位局限性问题，因此选择在Sobel算子优点的基础上对传统梯度清晰度算法进行改进。可以增加Sobel 算子梯度方向至4 方向（考虑到计算效率问题，不宜增加过多模板）改善方位局限性问题，结合自适应中值滤波和改进的最大类间自适应阈值算法实现图像清晰度计算，用以提升评价函数整体抗噪性、准确性和灵敏度。

1 传统梯度图像清晰度评价函数介绍

目前较为常用的图像清晰度评价函数主要有空域函数、频域函数、信息学函数和统计学函数四大类[8]。其中，频域函数计算量大，不适于快速测量计算；信息学函数计算结果波动较大；统计学函数的计算结果精度较低。相较而言空域函数，即梯度评价函数计算简单，其利用边缘灰度梯度变化来评价图像清晰度，可识别更多灰度梯度变化，使其调焦范围大、稳定性好，应用范围更加广泛。本节先介绍几种常用的传统灰度梯度函数，用来与改进后的清晰度评价函数的性能进行对比。

常用的梯度函数有能量梯度函数（EOG）、Roberts 函 数、Tenengrad 函 数、Brenner 函 数、方 差Variance 函数、拉普拉斯Laplace 函数等[9]。处理图像时可以把图像看作二维的离散矩阵，然后利用梯度函数获取灰度图像信息，用梯度值来评价图像的清晰度。本节中假设图像为I，其尺寸大小为M×N，图像I中某像素点（x，y）的灰度值为f（x，y），图像清晰度评价值为F。

（1）能量梯度函数（EOG）

能量梯度函数是将图像水平和与垂直方向相邻的像素点的灰度值做差，再进行平方运算，然后将逐个平方差运算的和作为评价值。定义如下：

（2）Roberts 函数

Roberts 函数主要是利用对角线方向像素点灰度值差的平方和作为每个像素点新的梯度值，所有像素梯度值的累加和即为清晰度值。定义如下：

（3）Sobel 算子函数

Sobel 算子清晰度函数是将图像与Sobel 算子水平、垂直方向模板卷积计算梯度值，再将梯度平方和作为清晰度值。Sobel 算子两方向模板如下：

式中，gx、gy分别代表Sobel 算子水平方向、垂直方向的模板。基于Sobel 算子的图像清晰度函数F定义，公式如下：

式中，T为阈值；G(x,y) 为像素点(x,y) 处新的梯度值。定义为：

式中，Gx(x,y) 和Gy(x,y) 分别代表像素点(x,y) 与水平、垂直方向模板上卷积的梯度值。其定义式如下：

（4）Brenner 函数

Brenner 函数是将相邻两个像素点灰度之差的平方累加作为清晰度值，优点是计算量小、灵敏度高，缺点是对噪声比较敏感。其定义式如下：

Brenner 梯度算子可以看作是模板T=[-1 0 1]与对应位置的像素依次卷积，模板T=[-1 0 1]是一个带通滤波器，Brenner 梯度算子就是通过带通滤波来滤除大比例的低频能量，保留中频能量。

（5）方差函数（Variance）

方差函数Variance 可以用来表示图像灰度信息的离散水平。处在焦点位置的图像灰度变化明显，离散水平高，方差大，而其他位置灰度变化小，方差也相对较小[10]。因此可以用灰度变化的平均程度来评判图像是否正确对焦。图像清晰度评价值如下：

式中，μ为图像的平均灰度。

式中，M、N是图像的尺寸。

（6）Laplace 函数

Laplace 函数是将灰度图像各个像素点与Laplace 算子模板进行卷积运算，得到梯度矩阵G(x,y)，取G(x,y)的平方和作为评价值，公式如下：

Laplace 算子如下所示：

以上就是常用的梯度图像清晰度评价函数，不同的梯度评价函数因为评价方法计算方式不同，而拥有不同的优点和特点。但都普遍存在一个问题，在外部噪声的干扰下，传统梯度评价函数容易出现局部最值，评价曲线波动较大，灵敏度大大降低，不利于对焦。因此在传统梯度函数基础上，提出一种计算简单、灵敏度高、抗噪性强的图像清晰度函数对提高自动对焦精度具有重要意义。

2 改进的Sobel算子图像清晰度算法

传统的基于Sobel 算子的清晰度函数只使用水平和垂直两个方向的模板，方位局限、边缘定位不够准确并对含有噪声的图像较为敏感，清晰度曲线灵敏度低，不利于后续自动对焦。因此可以采取增加方向模板的方式对算子进行改进，因考虑到计算效率的问题，只增加对角线模板至四方向模板（0°、45°、90°、135°），同时结合自适应中值滤波算法和自适应全局阈值增强图像目标边缘强度，提升算法抗噪性，使用强边缘像素点的梯度平方和作为清晰度值，在一定程度上改善了方位局限性问题，并且提升了算法抗噪性和灵敏度。改进的Sobel 算子图像清晰度算法主要分为三个部分：图像预处理、Sobel 梯度值计算、阈值确定边缘进行清晰度值计算。流程图如图1 所示。

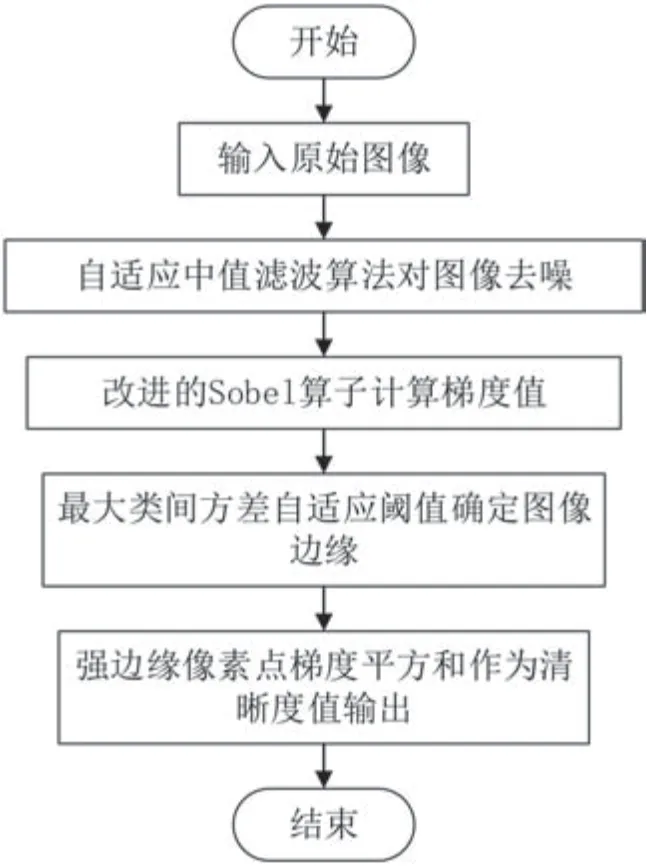
图1 改进算法流程图

2.1 自适应中值去噪

图像传感器CCD 在获取和传输图像过程中会引入各种噪声，这些噪声对图像清晰度值计算影响特别大，不利于对焦，所以在对图像进行清晰度值计算之前需要对图像进行去噪预处理，减少噪声对评价算法的影响。

图像滤波算法在空域和频域上可分为空间域滤波和频域滤波，空间域滤波法大多为点运算与小区域运算，速度快、计算量小；频域滤波需要对图像进行频域时域变换以及逆变换，算法较为复杂，处理速度慢。空间域滤波主要通过分析噪声在图像空间上的分布特性来去除噪声，常用的空间域滤波方法有均值滤波、中值滤波、统计排序滤波和自适应滤波等；中值滤波器的性能优于均值滤波器，故本文采用自适应中值滤波器进行图像去噪。

符号定义如表1 所示。

表1 自适应中值滤波符号定义

自适应中值滤波算法主要被分为两个过程：A层和B层，描述如下：

A层：若区域内最小灰度值、最大灰度值和灰度中值满足Zmin＜Zmed＜Zmax，则转到B层，否则增大窗口尺寸；如果窗口尺寸≤Ωmax，则重复A层，否则输出Zmed。

B层：如果满足关系式Zmin＜Zxy＜Zmax，则 输出Zxy，否则输出Zmed。

自适应中值去噪算法考虑了被处理像素点Zxy灰度值的情况，根据Zxy的大小决定是否需要进行滤波处理，自适应中值滤波器只有在满足条件Zxy=Zmin或Zxy=Zmax时才会改变被处理点的灰度值[11]，因此可以减少滤波过程中出现图像失真的问题。该算法的处理过程如下：

（1）在以被处理点Zxy为中心的一个自定义窗口对像素点进行排序，找到灰度中值Zmed；

（2）若灰度中值Zmed满足Zmed=Zmin或Zmed=Zmax，则增大窗口，重复步骤（1）；

（3）若灰度中值Zmed满足Zmin＜Zmed＜Zmax，则需要查看被处理点Zxy的灰度值；

（4）若关系式Zmin＜Zmed＜Zmax成立，则保持被处理像素点Zxy灰度值不变；

（5）若Zxy=Zmin或Zxy=Zmax，说明Zxy是考察窗口内的灰度极值，这时需要将被处理像素点的值替换为灰度中值Zmed。

2.2 四方向Sobel 算子梯度计算

传统Sobel 算子只有水平和垂直两方向的模板，算法简单，计算量小，但对除水平和垂直方向以外的其他方向边缘并不敏感，尤其是受噪声干扰纹理复杂的显微图像，检测效果不佳，抗噪性差。本文将传统Sobel 算子的方向模板由两个增加到了四个，可检测水平、垂直和对角线多个方向的边缘，改善了传统Sobel 算子方位局限性的问题，使边缘检测和梯度计算结果更加准确。四方向Sobel 算子如下：

其中h1、h2分别代表水平和垂直方向模板；h3、h4代表两个对角线方向模板。实际上图像的梯度方向可以取0°～360°这个范围内任何值，但是考虑到计算效率和边缘宽度限制等问题，故只定义了四个方向模板。虽然继续增加模板的数量可以进一步提高检测的准确性，但同时也降低了运算速度。传统Sobel 算子处理一帧图片需要916 ms，本文改进的Sobel 算子处理一帧图片需要773 ms，相比传统Sobel 算子运算速度提升了15.6%。

扩展了方向模板后，需要将图像与大小为3×3 的4 方向模板进行邻域卷积计算，重新计算像素点梯度值。图像中每个像素点的卷积计算公式如下：

其中，G1(x,y)、G2(x,y)、G3(x,y)、G4(x,y) 分别代表灰度图像中每个像素点的水平方向（0°）、垂直方向（90°）和对角线方向（45°、135°）的卷积梯度值。计算完每个像素点四方向模板的卷积值后，采用范数为1 来计算像素边缘强度值，即将水平方向、垂直方向和对角线方向卷积的绝对值之和作为中心梯度值，避免了以范数2 计算中的开方与平方运算，提升了运算速度。最终可以得到新的梯度图像F(x,y)，则新的梯度图像像素点的梯度计算公式如下：

2.3 自适应阈值强边缘像素点提取

获得新的梯度图像后，需要对图像强边缘像素点进行提取，将强边缘像素点梯度平方和作为图像清晰度值，这时需要选取合适的阈值对图像进行分割。

目前主要有两种自适应阈值选取的方法：基于最大熵原理的自适应阈值选取和基于Otsu 方法的自适应阈值选取[12]。最大类间方差法不能准确地将目标与背景分开，目标边缘模糊且背景噪声大[13]。故采用一种改进的最大类间方差法对图像进行自适应阈值提取强边缘像素点，并计算图像清晰度值。

改进的最大类间方差自适应阈值选取主要思想为：依据图像灰度范围，把图像分割为C0和C1两个部分。本节中设图像的灰度取值范围为[0，L-1]，自适应分割阈值为T，则C0={0，1，2，…，T}，C1={T+1，…，L-1}，各个像素点的平均梯度值如下：

式中，F(x,y)为灰度梯度图像像素点的梯度值；ni为灰度值为i的频数；Wi为每一个像素点的梯度值；Hi为各个像素点的平均梯度值；Wi={(x,y)I(x,y) =i}。像素均值和梯度方差的计算如下：

式中，T和L分别为分割出两个区域C0和C1的灰度范围；μ0、μ1为两类像素各自的均值；为各部分的梯度方差。灰度值梯度均值方差最大的阈值T计算公式如下：

由公式（20）可知，当两方差乘积为最大时，对应的阈值T即为最佳阈值。

根据自适应阈值T提取图像强边缘像素点，将图像分割成目标和背景两个部分。将强边缘像素点即像素点梯度值大于等于阈值T的梯度平方和作为图像的清晰度评价值，清晰度值计算公式如下：

式中，M为被处理图像的清晰度值，该结果可用于后续对焦处理。

3 实验结果与分析

3.1 实验设备

为了验证改进的Sobel 算子图像清晰度算法的性能，用HAYAER300 倍变倍显微镜头在环形光源辅助下，借助机械调焦装置等步长调节显微镜与被测物体间距离，通过CCD 和图像采集卡获取被测物体一系列离焦、聚焦图片序列；然后在Win10 操作系统下通过Matlab 软件分别对改进算法的边缘检测效果、抗噪性和灵敏度进行了仿真实验与计算。CCD 型号为IMPERX_bobcat-B2520，分辨率为2 448×2 050，像元尺寸为3.45 mm，感光芯片尺寸为66.93 mm，环形光源为LED 可见光。图2 为实验图像采集设备图。

图2 图像采集设备图

3.2 边缘检测效果实验分析

为验证改进算法对目标定位的准确性，将改进算法与传统Sobel 算子边缘检测效果进行实验对比。实验采用直径为3 mm 螺母在显微镜下离焦、聚焦、离焦图像序列来进行测试。下面选用其中两幅离焦和聚焦图片，如图3 所示，进行边缘检测效果对比，实验结果如图4、图5 所示。

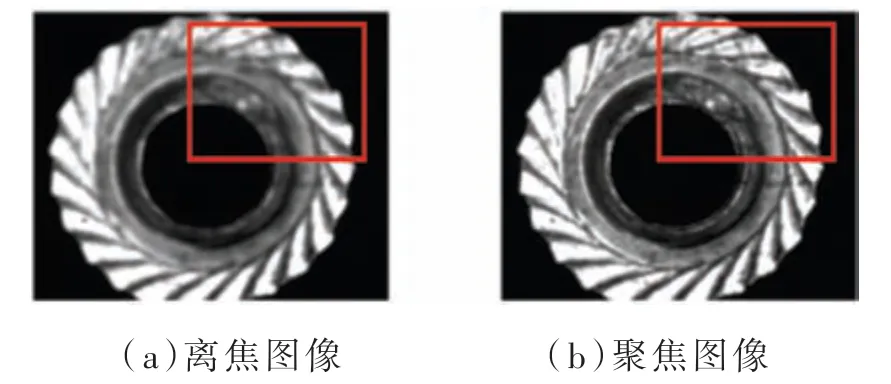
图3 部分图像序列

图4 传统Sobel 边缘检测

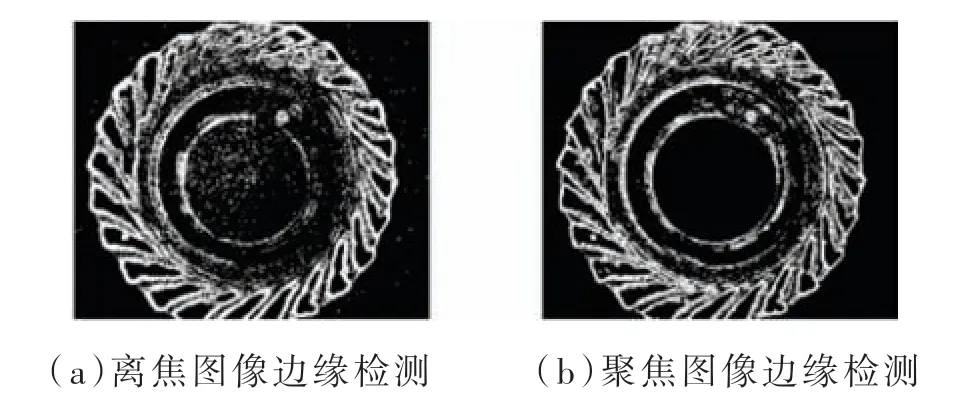
图5 改进算法边缘检测

图4 是传统Sobel 算子对螺母的边缘检测效果图，从图中可以看出传统Sobel 算子由于其方位局限性问题，对目标定位不够准确，丢失了很多目标像素点，边缘检测效果不好。图5 是本文改进算法边缘检测效果图，可以看出目标轮廓清晰，目标边界得到增强，同传统Sobel 算法相比图像边缘定位更加准确，弥补了传统算法上方位局限性的不足。

3.3 改进算法抗噪性实验分析

CCD 在获取图像的过程中，会引入各种类型噪声，比如由于发热或照明引入的高斯噪声，传输过程中引入的椒盐噪声等。为了对改进算法的抗噪性进行验证，对图像序列分别添加椒盐噪声和高斯噪声，并将改进算法分别与传统Sobel 算法和传统梯度评价函数进行对比。这里选用螺母图像序列和文字图像序列作为实验对象，并对它们添加不同种类噪声进行抗噪性实验分析，两组实验图像序列如图6、图7 所示，这里只展示部分图像序列。

图6 螺母图像序列

图7 文字图像序列

对螺母序列和文字序列分别添加椒盐噪声和高斯噪声，然后对加噪后的全部图像序列进行清晰度评价，将改进的Sobel 算法和传统Sobel算法比较，并将清晰度值归一化处理，最终得到两种算法的清晰度评价曲线。实验结果如图8、图9 所示。

图8 添加不同噪声后螺母的图像清晰度评价曲线

图9 添加不同噪声后文字的图像清晰度评价曲线

图8、图9 是分别添加椒盐噪声和高斯噪声后两组图像序列的评价曲线，从中可以看出传统Sobel 算子清晰度评价函数对噪声敏感，在椒盐噪声影响下灵敏度低，在高斯噪声影响下还会出现局部最大值，稳定性较差；相比之下，改进的Sobel 算子清晰度评价函数无论在椒盐噪声还是高斯噪声的影响下仍能保持良好的单峰性，不存在局部多个最值的情况，具有良好的抗噪性和灵敏度。

接下来分别给两组图像序列添加噪声密度为0.1、0.25 的椒盐噪声以及均值为0，方差为0.02、0.05 的高斯噪声，检验本文改进算法与常用的灰度梯度图像清晰度评价函数的抗噪性。归一化的图像清晰度评价曲线如图10、图11 所示。

图10 不同椒盐、高斯噪声影响下螺母序列图像清晰度评价曲线

图11 不同椒盐、高斯噪声影响下文字序列图像清晰度评价曲线

从图10、图11 中可以看出常用的图像清晰度函数极易受噪声影响，在椒盐噪声影响下容易出现灵敏度低、单峰性差的问题，即评价曲线上升下降缓慢；在高斯噪声的影响下，常用的清晰度评价函数容易出现局部最大值最小值的情况，不能准确捕获到图像清晰度最佳的图像所对应的位置。本文改进的基于Sobel 算子的图像清晰度函数，不论是在椒盐噪声影响下还是高斯噪声影响下都能保持住良好的单峰性和无偏性，并且灵敏度较高，相比传统的灰度梯度清晰度评价函数具有更加突出的抗噪性。

3.4 改进算法灵敏度实验分析

图像清晰度函数是用来指导调焦机构找到最佳成像位置的评价函数，高灵敏度是一个评价函数的最基本要求。灵敏度在视觉上表现为评价曲线的陡峭程度，越陡则表明灵敏度越高。为了对本文改进算法的灵敏度进行定量分析，对显微图像序列进行灵敏度评估，采用灵敏度因子来评估图像的灵敏度，本文d定为偏离正焦位置一帧图。灵敏度因子的计算公式如下：

式中，Msen表示评价函数的灵敏度因子；Mmax表示最佳成像位置即正焦位置处图像清晰度值；Mmax+δ表示偏离正焦d位置处图像清晰度值，d表示横坐标偏移量。表2为不同清晰度评价函数的灵敏度因子。

表2 不同评价函数灵敏度因子

从表2 中可以看出改进的基于Sobel 算子的图像清晰度函数灵敏度因子比传统的灰度梯度函数灵敏度更高，评价曲线更陡即曲线单调的一侧斜率大。本文改进算法相比传统Sobel 算子函数灵敏度因子提升了0.578 5，相较于传统灰度梯度函数提升了0.578 5～0.829 5，平均灵敏度因子提升了0.711 9，并且本文改进算法在噪声干扰下还能保持良好的稳定性，左右两侧单调性好，不存在局部最值，评价曲线无波动性。

4 结论

本文介绍了空间域类梯度评价函数，分析了各自优缺点，在传统的梯度函数基础上，针对传统梯度函数抗噪性差的问题，提出了一种改进的Sobel 算子图像清晰度评价函数，结合了自适应中值滤波器和最大类间自适应阈值法，提升了算法抗噪性和灵敏度。通过实验证明，本文改进的算法在运行速度和灵敏度因子上分别提高了15.6%和0.711 9，相比传统的灰度梯度评价函数具有单峰性好、灵敏度高、抗噪性好的特点，有利于自动对焦系统的优化。