基于阿基米德螺旋加密重构技术的无人航行器KT 辨识研究

韩璐羽，白佳钰，于曹阳，连 琏,2

(1.上海交通大学海洋学院，上海 200030；2.上海交通大学海洋工程国家重点实验室，上海 200240)

0 引言

近年来，无人航行器被广泛应用于海洋科学与工程任务，建立高精度操纵模型是航行器设计、优化与控制的基础。目前常用的Abkowitz 整体模型和MMG分离模型中水动力参数较多，相应的辨识系统输入矩阵维度增加，辨识计算量较大[1]；而Notomo提出的操纵响应方程参数较少、计算简捷且可直接从约定试验中获得，这有利于提高运动控制、性能预测等的实时性，在无人航行器研究领域得到广泛应用。

精确辨识方程中各水动力系数是优化建模的关键一环。传统系统辨识方法包括最小二乘法(least square,LS)[2–3]、极大似然法(maximum likelihood,ML)[4]、卡尔曼滤波法(Kalman filter,KF)及其拓展[5–6]等，基于现代人工智能技术又发展出了人工神经网络(artificial neural network,ANN)[7]和支持向量机(support vector machine,SVM)[8]等方法。孙功武等[3]优化最小二乘法，提出了一种基于模糊控制的动态遗忘因子迭代最小二乘(recursive least square,RLS)算法，实现了遗忘因子针对误差的动态调整，有优越的辨识精度与收敛速度。褚式新等[4]根据辨识原理与前向差分法设计了一种极大似然辨识方法，较传统卡尔曼滤波算法预报更为精准。秦操[6]采用无迹卡尔曼滤波(unscented Kalman filter,UKF)算法，设计分步辨识，有效提高了辨识精度。以上研究侧重于在现有试验数据的基础上，改进算法以提高收敛速度以及辨识精度。

但在系统辨识算法已较为成熟的情况下，用于计算的航向数据质量对精度影响可能更为显著。动态试验中，航向传感器的数据采集频率与精度相互制约[9–10]，不足以支持高精度的模型辨识。当前技术水平限制下，对稀疏数据进行插值重构是高效提高辨识精度的重要途径。常用的插值方法有拉格朗日插值、分段线性插值、三次样条插值等，但三者重构的光滑程度不完全符合无人航行器航向随时间光滑连续变化的实际情境[11 –12]。

阿基米德螺旋(Archimedesspiral, AS)在变量光滑连续变化方面具有较大优势。现有研究中，AS结构多用于平面天线的设计与实现[13–14]。此外，在对非圆二次曲线与样条曲线轮廓机械加工时，应用AS拟合离散点，较一系列折线、圆弧等，实现了确保精度前提下的计算量减少[15]。本文尝试将AS应用于初始航向数据的插值重构，探索该方法在操纵辨识数据预处理方面的更大潜力，对于优化原始稀疏数据以得到更为精准的操纵模型有重要意义。

本文首先引入无人航行器一阶线性响应模型，使用采样频率不同的数据集进行参数辨识，揭示航向预测精度与采样频率的关系；之后，使用AS插值重构数据，改善最小二乘算法在初始采样数据稀疏时的辨识精度。最后，通过与初始稀疏数据集、基于三次样条插值的加密集辨识结果对比，证明AS插值方法的优越性。

1 无人航行器操纵运动数学模型

为实现对无人航行器航向的精准预测与控制，需建立其航向角与垂直舵角之间的响应方程。假定前向速度恒定，忽略横摇、纵倾和浮潜自由度耦合的影响，无人航行器的水平面动力学方程可简化为[16]：

式中：m为 无人航行器的质量；mii(i=1,2,6)表示其附加质量；Y∗和N∗为 线性/非线性水动力系数；Y和N为无人航行器驱动执行器产生的侧向推力及偏航力矩；Iz表示绕z轴的惯性矩。

假设仅小舵角操纵无人航行器，则式(1)可进一步简化为：

式(2)经变换，得到：

式中： δ为舵角，rad；T1，T2，T3为时间常数，s，表征无人航行器的应舵性和航向稳定性；K为舵角增益，s−1，也称旋回性指数。上述K和T参数具体表达为：

式(3)即为日本Notomo教授提出的一般性首摇响应线性方程，通常称作二阶线性KT方程。本文侧重于探究响应方程参数辨识过程中由于输入数据“航向-舵角”稀疏产生的问题及相应优化方法。为此，在操舵不很频繁的前提下，参数辨识与设计优化阶段选取进一步简化的一阶线性KT模型：

也可用航向角 φ(rad)表示为：

式中：

2 响应模型参数辨识及辨识精度判定原理

2.1 基于最小二乘算法的响应模型参数辨识

对一阶线性KT 模型进行参数辨识时，首先将式(9)作离散化处理，即用向前差分代替原本微分形式。整理得：

式中： ∆t表示航向/舵角传感器两次采样的间隔时长，s；φ(t) 和δ (t) 分别为t时刻无人航行器航向角和舵角。

将式(11)表达为矩阵形式，即可得到最小二乘法的标准辨识模型AX=b。矩阵具体表达为：

输出矩阵

输入矩阵

参数矩阵

此参数矩阵X的最小二乘解为：

因此，将操纵试验中航向/舵角传感器采集的数据依次代入输入矩阵和输出矩阵，即可解得式(9)中一阶线性响应模型的K和T参数。

2.2 参数辨识精度的判定

为确定K和T的辨识精度，将式(11)整理得到如下递推关系式：

代入初始采样数据集 ∆t，t和δ(t)等数据以及辨识所得参数K和T，预测无人航行器航向角φ′(t)。通过与操纵试验 φ(t)对比，计算各时刻绝对误差和总均方根误差作为参数辨识精度的定量判定标准。

3 数据采样频率对辨识精度影响的定量分析

3.1 参数辨识输入矩阵数据采集

Z 形操纵试验于1943年由Kempt 提出，用于衡量船舶操纵性能，目前被广泛应用于无人航行器性能分析，是确定参数K和T的标准方法。本文利用文献[17]中模型数据，以Matlab为平台，开展15°Z 形全数字仿真试验。仿真采样时间间隔为0.1 s，采样总时长为20 s，所得数据如图1所示。

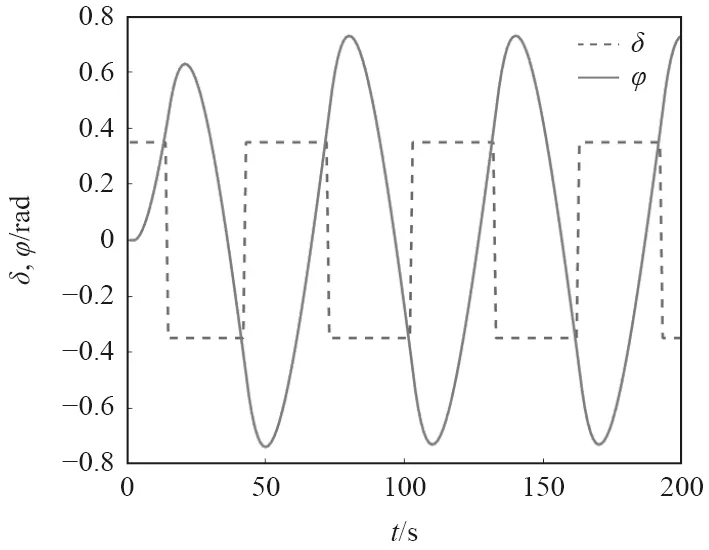
图1 15° Z形仿真试验数据Fig.1 Data in 15° zigzag simulation

3.2 输入矩阵采样频率对辨识精度的影响分析

基于图1中的仿真数据，建立初始采样数据集S0。从S0中取时间间隔放大为0.5 s和0.2 s 的数据，即分别取t=0.5 s，t=1 s，…，t= 20 s 和t= 0.2 s，t=0.4 s，…，t=20 s 时舵角 δ(t)和航向角φ(t)，构成稀疏数据集S1和S1′。S0、S1和S1′数据如图2所示。

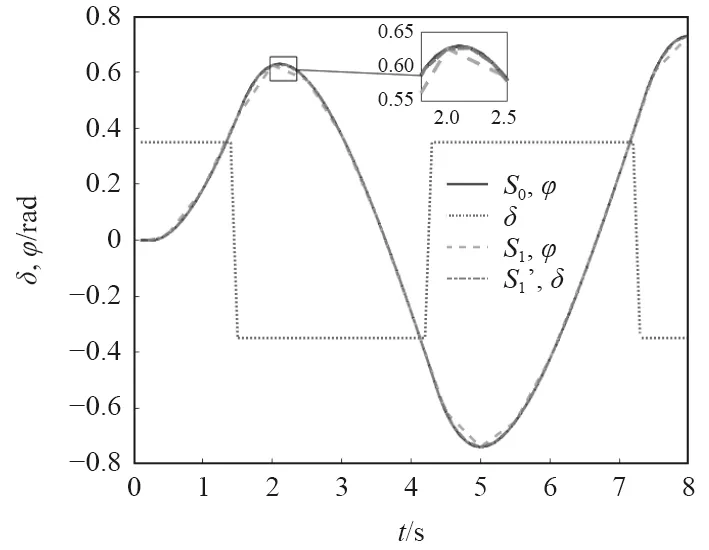
图2 不同采样频率数据集S0、S1和S1′对比图Fig.2 Comparison of data sets(S0,S1 and S1′)with different acquisition frequencies

对各数据集开展KT参数辨识，辨识结果如表1 所示。

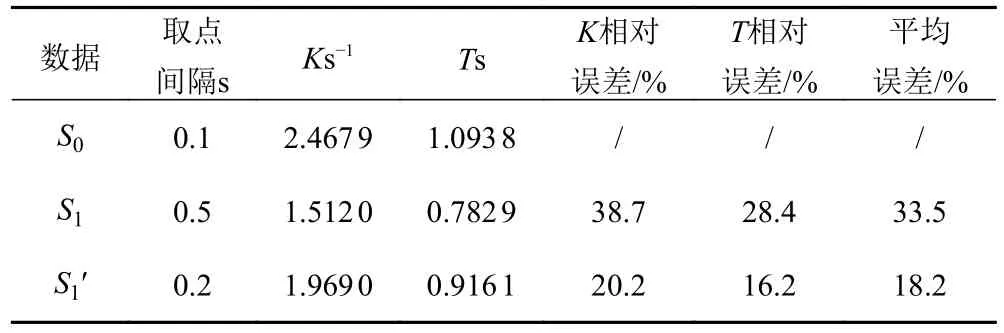
表1 S0，S1和S1′辨识结果对比Tab.1 Comparison of identification results using S0,S1 and S1′

利用上述3个数据集辨识得到的KT数据，辅以式(16)得到无人航行器的航向预测对比结果，如图3所示。

图3 S0、S1和S1′所得KT 模型对应的航向预测结果对比Fig.3 Comparison of heading results derived from three data sets(S0, S1 and S1′)

不同密度数据辨识的航向结果均与实测数据存在一定误差。S0模型预测的绝对误差在0.02 rad 以内，精度较高，能够满足无人航行器响应建模与路径预测的实际需求。然而，随着数据采集频率降低，数据集稀疏程度加深，相应的辨识误差增大，说明有必要保持一定的数据采集密度。在航向/舵角传感器数据采集频率固定的情况下，应用合适的数据插值加密方法对参数辨识输入矩阵预先进行优化处理，有利于得到高精度无人航行器KT响应模型。

4 基于阿基米德螺旋(AS)重构加密的改进辨识

4.1 稀疏数据集AS插值重构

阿基米德螺旋(AS)的极坐标表达形式如下：

式中：r和 θ分 别为极径和极角，θ ∈[0,θmax]；k为正常数。

选取采样间隔为0.5 s的数据集S1进行重构，以t和 φ为基本变量。设第i个数据点为Ai(ti,φi)(i=1,2,3,…)，Ai与Ai+1之 间采用AS几何连接，记作ASi，参数化表达为：

式中： ρ为依据Ai与Ai+1相对位置关系确定的AS螺旋方向， ρ=1表示螺旋路径从极坐标的原点(Ai)按顺时针方向传播； ρ=−1即按逆时针方向传播； σ表示螺旋初始角度。由于需给定螺旋初始方向，插值至少从采集的第2个数据点(A2)开始，由A2与前点A1确定 σ。ρ和σ 的表达式如下：

为尽可能缩小时间维度响应不足对 σ值的影响，设Ai与Ai−1离散化插值所得点中最接近Ai−1者 为B(i−1)ilast(i>2)，将σ计算调整为：

每段AS重构终止于点Ai+1(ti+1,φi+1)，以此为边界条件，给定常数k和θmax。完成重构的数据集记作S2。

A1,…,A4数据点为例，重构方法示意如图4所示。

图4 AS插值重构方法示意图Fig.4 The schematic diagram of ASinterpolation method

4.2 重构数据集辨识效果对比

为了进一步体现AS重构加密的优越性，除将其模型参数辨识精度与原稀疏数据集S1对比外，还选取S1基于三次样条插值的加密集S3作为对照。S0，S1，S2和S3参数辨识结果如表2所示，航向预测精度对比分别如图5和图6所示。

由表2，图5和图6可以看出，重构加密后的数据集S2和S3较原稀疏数据模型辨识效果有明显改善，KT参数辨识精度显著提高，其中K的相对误差缩小至不到1%；基于KT模型的航向角预测结果绝对误差缩小了一个数量级。此外，AS弥补了三次样条插值光滑性不足的缺陷，更加符合Z 形操纵试验中航向角光滑连续变化的实际情景。图6表明，AS较三次样条重构加密精度提高了20%，展现了AS的卓越性。图5和图6表明，S2，数据集辨识已较为接近S0所得结果，很大程度上减小了传感器采样频率较低时对无人航行器响应模型辨识的影响。

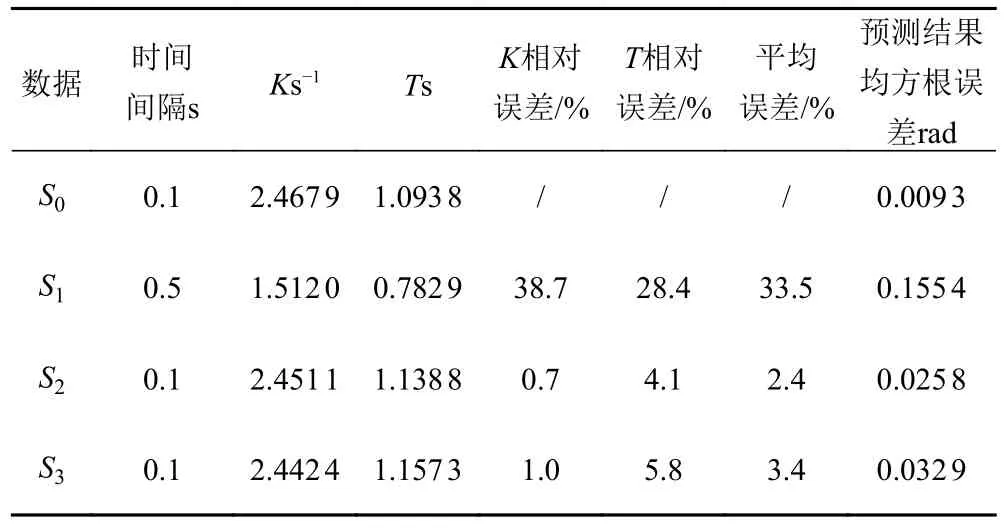
表2 S0，S1，S2和S3辨识结果对比Tab.2 Comparison of identified results of S0,S1,S2 and S3

图5 S0，S1和S2 所得KT 模型预测结果对比Fig.5 Comparison of heading results derived from three data sets(S0,S1 and S2)

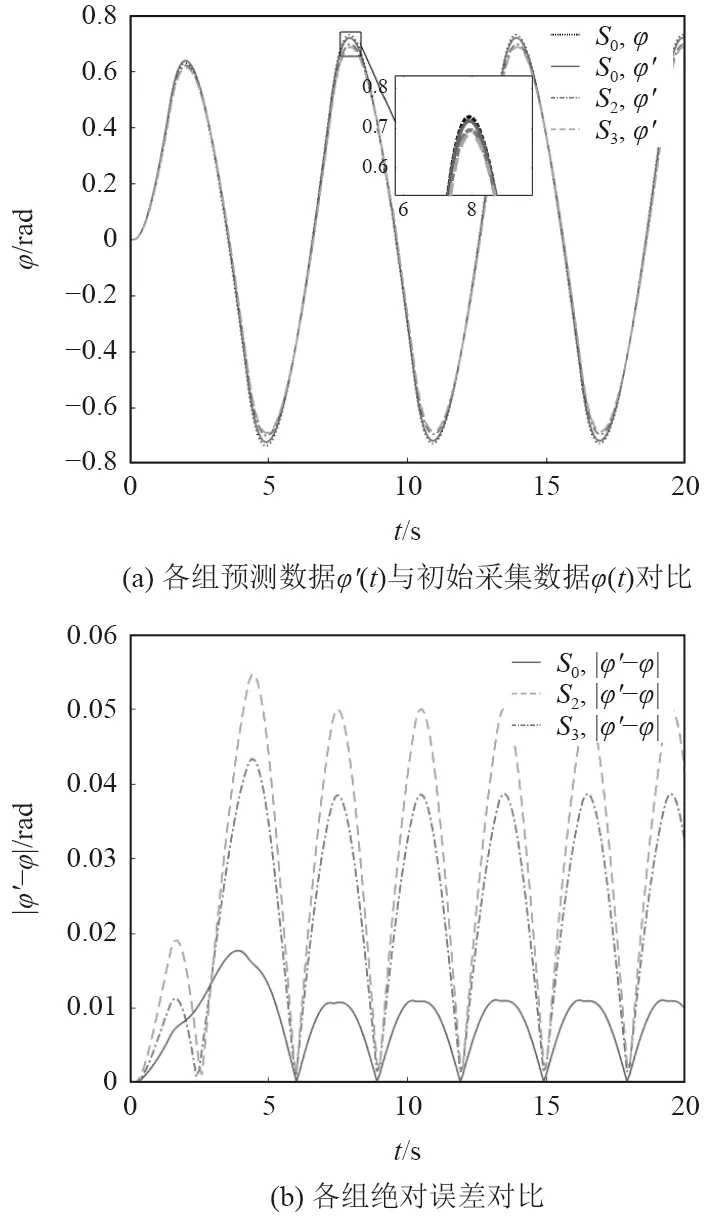
图6 S0，S2 和S3所得KT 模型预测结果对比Fig. 6 Comparison of heading resultsderived from three data sets(S0,S2 and S3)

5 结语

本文将阿基米德螺旋加密重构算法应用于Z 形操纵试验数据的插值优化中，并基于重构数据集进行一阶线性操纵响应方程的参数辨识。该方法优化了系统辨识算法在稀疏数据集上的表现，并且有效弥补了三次样条插值光滑程度有限的不足。本文从AS插值优化算法的引入必要性、数据预处理与辨识过程、辨识结果分析与对比等三方面展开研究，得到以下结论：

1）航向数据采集间隔由0.1 s 下降至0.5 s时，KT参数辨识平均误差增大了33.5%，说明数据采集频率对参数辨识精度有很大影响。

2）在数据采集频率受限的情况下，AS加密预处理的数据集与高精度高频率采样数据集的参数辨识平均误差仅相差2.4%。同时依据辨识所得模型预测航向，与实际仿真试验结果对比，均方根误差仅为0.0258 rad。表明AS插值优化算法提高稀疏数据集辨识精度的有效性。

3）与基于三次样条插值算法加密数据的效果对比表明，KT辨识与预测结果误差均有所下降，验证了AS在变量光滑连续变化方面具有较大优势，更适合航向数据优化的实际情境。