高效扭曲舵的水动力特性数值分析

王春鸽，胡传峰

(1.长江大学文理学院，湖北荆州 434000；2.湖北理工学院，湖北黄石 435003)

0 引言

船舵是船舶动力系统的关键部分，起到方向控制的作用，船舵产生作用的原理是舵与海水之间的流体动力学作用，在船舵表面产生力和力矩。正常情况下，船舵工作过程中海水不会对船舵造成结构的破坏，船舵设计只需要考虑流体作用在舵表面的压力和力矩，但是现在大量的船舵故障事故表明，船舵在船舶高速航行过程中，由于螺旋桨旋转造成的尾流，会对船舶的流体力学特性产生额外的影响。其中，船舵表面的空泡效应是影响最大的因素，在发生空泡效应时，船舵表面可能产生剥蚀[1]，空泡导致的结构异常振动会对船舵的连接结构产生不利影响。此外，空泡效应还会造成船舵工作效率的下降，对船舶动力系统的整体性能造成不利影响。

高效扭曲舵在应对船舶螺旋桨尾流等不利条件时具有明显的优势，本文在传统船舵结构的基础上提出一种新型扭曲剖面结构的船舵设计，改善船舵的压力分布，基于流体动力学仿真软件Fluent 进行了扭曲舵的流体动力学仿真。

1 船舶扭曲舵水动力分析的CFD基本理论

计算流体力学的基础是有限元理论，建立计算流体力学的有限单元模型如图1所示。

图1 计算流体力学的有限单元模型Fig.1 Finite element model of computational fluid dynamics

结合有限单元流体力学模型，可建立计算流体动力学的基本方程：

1）连续性方程

计算流体力学的连续性方程如下式：

其矢量式为：

式中：k为流体的粘性；ρ为密度；l，m，n为有限单元流体的速度分量。

2）能量守恒方程

有限单元对外做的功和热量损失与流体内能的增加量相同，利用计算流体力学的湍流模型，可以建立流体有限单元的能量守恒。

首先进行有限元体积的积分：

式中： φ为有限体积的函数变量； φ¯为函数均值。

建立有限体积的湍流模型如下式：

式中：Vi为流速； δ为液体的粘度系数；Gb为误差系数； ε为耗散系数，

进而建立流体有限单元的能量守恒方程如下式：

式中：E为流体内能；E0为流体对外的做功；P为流体压力；Vi，Vj分 别为流速； σk， σw分别为能量损耗系数。

3）动量守恒方程

根据牛顿第二定律F=ma，可得动量方程如下式：

2 船舶高效扭曲舵的水动力数值计算分析

船舶螺旋桨高速旋转会改变船舵的流场，因此，船舵工作过程中会产生较大的流体动压，同时产生船舵的侧向力。本文结合扭曲舵的侧向力进行结构优化设计，防止船舵出现空泡效应的同时，提高船舵的工作效率。

建立船舶扭曲舵的剖面力学模型图如图2所示。

图中，攻角 α为扭曲舵与水流方向的夹角[2–3]，P为扭曲舵在该剖面受到的压力，可分解为：

l为弦长，xt为压力中心，可求扭曲舵的压力分散系数为：

扭曲舵的水动力合力P可简化表示为：

式中：Ak为剖面的面积； η为粘度系数；v为流体相对运动速度；Re为雷诺数。

在该力学模型的坐标系下建立船舵的尾流运动方程为：

式中：Vm为速度分量；Sm为位置分量。

如前文所述，基于流体动力学理论，扭曲舵工作过程中始终满足连续性方程，即

式中：Ux，Uy，Uz为三坐标下的速度分量。

结合扭曲舵的受力特性，建立扭曲舵的能量守恒模型为：

式中：扭曲舵受到的压力为P；扭曲舵沿ox轴作用力为Fτx；沿oy轴的作用力为Fτy；沿oz轴的作用力为Fτz。

扭曲舵在工作过程中的作用力要大于敞水阻力，建立扭曲舵剖面面元的控制方程为：

其中：m为舵叶的质量； ∆w为 舵叶的面元参数；Hξ为体积参数； ψ为面积扩散系数，对面元进行积分可得剖面的控制方程：

3 基于Fluent 的高效扭曲舵的水动力特性仿真

结合扭曲舵的流体动力学特性，基于Fluent 软件进行船舵的水动力仿真。

1）船舵参数的确定

为了提高仿真效率，在选用船舵仿真模型时，采用经典NACA 剖面，该剖面作为成熟的数学模型，在船舵设计过程中应用频次很高。

NACA 船舵的剖面参数如表1所示。

表1 NACA 船舵的剖面参数表Tab.1 Profile parameters of NACA rudder

2）有限元建模

有限元模型最终决定的是水动力仿真的精度，与静力学有限元仿真不同，基于Fluent 的流体动力学模型更加注重流场的有限元建模。

为了保证扭曲舵有限元仿真的效率和精度，采用结构化网格建模思路[3]，使用O-H 型网格，针对船舵的攻角位置和尾部进行适当加密，图3为扭曲舵表面的有限元建模示意图。

图3 扭曲舵表面有限元建模示意图Fig.3 Schematic diagram of finite element modeling for twisted rudder surface

3）流场建模

选择扭曲舵的流场计算区域为长方体，扭曲舵计算域中静止不动，水流以速度Vm流向扭曲舵。扭曲舵计算域流场建模示意图如图4所示。

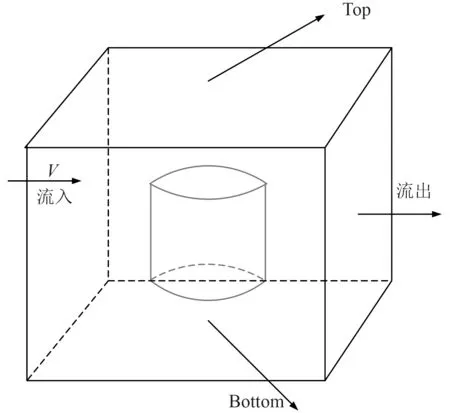
图4 扭曲舵计算域流场建模示意图Fig.4 Schematic diagram of flow field modeling in the calculation domain of twisted rudder

流场建模需要注意以下边界条件：

①入流面的选择

针对NACA 剖面模型选择入流面为弦长0.8 m 附近，并在入流面建立流体速度边界条件。在计算域对称位置设置出流面，并设置出流速度也为Vm。

②对称边界

根据船舵结构特征，在底部4倍弦长位置设计对称边界条件，对称面的设计一方面能够简化计算，另一方面也能提高运算的收敛性。

忽略兴波阻力的影响，忽略扭曲舵的表面滑移。

4）属性参数赋值和求解

在Fluent 仿真程序中进行属性参数的赋值，设置阻力系数误差范围10%，舵角40°时阻力系数最大；设置流体密度 ρ=1 000 kg/m3，粘度系数 η=0.5。

速度-压力的耦合算法为SIMPLE经典算法[4]，求解器选择为Pressure-Based，采用压力修正。

图5为不同仿真边界得到的阻力系数对比。

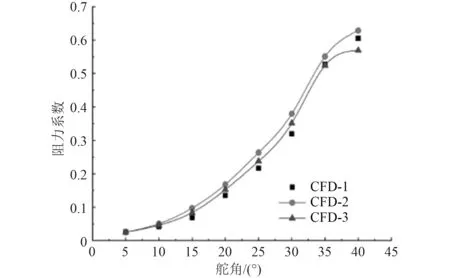
图5 不同仿真边界得到的阻力系数对比Fig.5 Comparison of resistance coefficientsobtained from different simulation boundaries

图中，CFD-1，CFD-2，CFD-3分别为液体流速5，6，7 m/s 的对比。

4 结语

扭曲舵在应对螺旋桨尾流等恶劣工况时具有更好的流体动力学性能，本文基于流体动力学基础和有限积分法，对扭曲舵的流体动力学特性进行建模，利用CFD软件Fluent 进行了阻力特性的流体力学仿真，实现扭曲舵的最优参数设计。