一种改进的三维空间中基于随机Hough变换的航迹起始方法

周立

关键词：三维Hough变换；航迹起始；强杂波环境；低概率截获

1引言

航迹起始是多目标航迹跟踪处理中的基础，是否能正确起始航迹与航迹正确率和质量直接相关。在航迹起始阶段，由于量测精度低、环境杂波、虚假目标等因素，会将真实航迹淹没在大量虚假点迹中。同时，由于目标距离远、雷达散射截面积受照射姿态异常分布或地物遮蔽等因素的影响，截获概率可能降低，目标点不连续。这些问题对航迹起始带来了一定的挑战[1]。

传统的航迹起始方法有两大类：顺序处理技术和批处理技术。顺序数据处理技术，包括逻辑法、直观法及其衍生算法等，在强杂波环境下，其不仅会形成大量虚假航迹，还会影响真实航迹的起始：批数据处理技术，包括标准Hough变换法、修正的Hough变换法、随机Hough变换法等[2]，能消除部分强杂波环境的影响，但只能在目标回波连续的情况下才能体现其较好的性能，且目前针对三维空间中的Hough变换及其衍生算法的研究较少。在工程实际中，往往是强杂波环境和目标回波不连续同时存在，在低概率截获情况下，现有的航迹起始方法无法有效起始航迹。本文基于以上背景，提出了一种改进的三维空间中基于随机Hough变换的航迹起始方法，该方法利用速度门限，以减少计算量、增加正确性；并利用周期时序特性进行限制，以消除低概率截获的影响，在低概率截获伴强杂波环境下也能体现其较好的性能[3-5]。

2传统的三维Hough变换法及其衍生算法

Hough变换是检测图像空间中图像特征的一种基本方法，主要适用于检测图像空间中的直线。三维的Hough变换通过式（1）将笛卡尔坐标系中的观测数据变换到参数空间中的坐标，即：式中，p，8G[0，180°]。

笛卡尔三维空间中的一条直线可以通过原点到这条直线的法线距离Po，Po与x-y平面的夹角00和Po在x-y平面的投影与x轴的夹角80来定义。如图1、图2所示，笛卡尔坐标系中的任一点（x，y，x）可通过式转换成参数空间中的一个曲面，将笛卡尔空间中的一条直线上按一定频率采样，得到若干点，并将这些点转换到参数空间中，进而得到若干曲面，且这些曲面相交于一点；同理，在参数空间中，每一个曲面对应笛卡尔空间中的一个点，若参数空间中的多个曲面交于一点，则这些曲面所对应的笛卡尔空间的点也在一条直线上。

2.1标准Hough变换

标准Hough变换将p-0-8参数空间按照一定间隔离散地分割成若干小方格，对量测得到的x-y-z空间内的每一个数据点（x，Y，x）进行Hough变换，若x-y-z空间内存在直线，则这些直线上的点所对应的p-0-8空间内曲面的交点会聚集在p-0-8空间相应的小方格内。经过多个周期累积，对于直线运动的目标，p-0-8空间中某一个特定方格中点的数量会得到累积。对方格中的点数进行峰值提取，若中心点为（pk，Ok，8k）的小方格中点的个数超过门限值，则认为x-y-z空间中存在一条参数为pk，Ok，8k的直线。基于以上信息，可进行点迹提取用来起始航迹。

基于标准Hough变换的方法，往往多次扫描之后才能有较好的航迹起始效果，且计算量很大，不符合实际工程需要：方格如何选取、峰值如何定义目前也没有定论。其次，标准的Hough变化的方法没有考虑点迹的时序信息，无法获得航迹起始的时刻，在强杂波环境下，也容易将同一周期的多个杂波点检测成一条直线，从而产生大量虚假航迹[6]。

2.2修正的Hough变换

修正的Hough变换考虑了各点迹的时序信息，并加入速度选通，减少了虚假航迹。其算法可描述为：雷达在第n，n+1，n+2次扫描时刻接收到的量测值分别为，可将这三组数据通过式（1）转换到p-0-8空间，得到三个曲面。可得差分函数：

2.3随机Hough变换

随机Hough变换的做法是：每次从所有量测中随机选取两点，确定对应的，当达到最大采样次数时，提取累计次数达到设定门限的，以确定航迹。该方法仍然没有考虑扫描时序，在杂波点较多时，容易产生虚假航迹。有文献采取逐拍采样的方式，即每次选取的两个点是相邻周期的，此时，若雷达因远距探测威力不足，或由于环境遮挡等因素，则导致截获概率低，即对于某一目标，并非每一周期都能截获，此时无法对相邻两个周期的数据进行关联，也无法成功起始航迹。

3改进的基于随机Hough变换的航迹起始方法

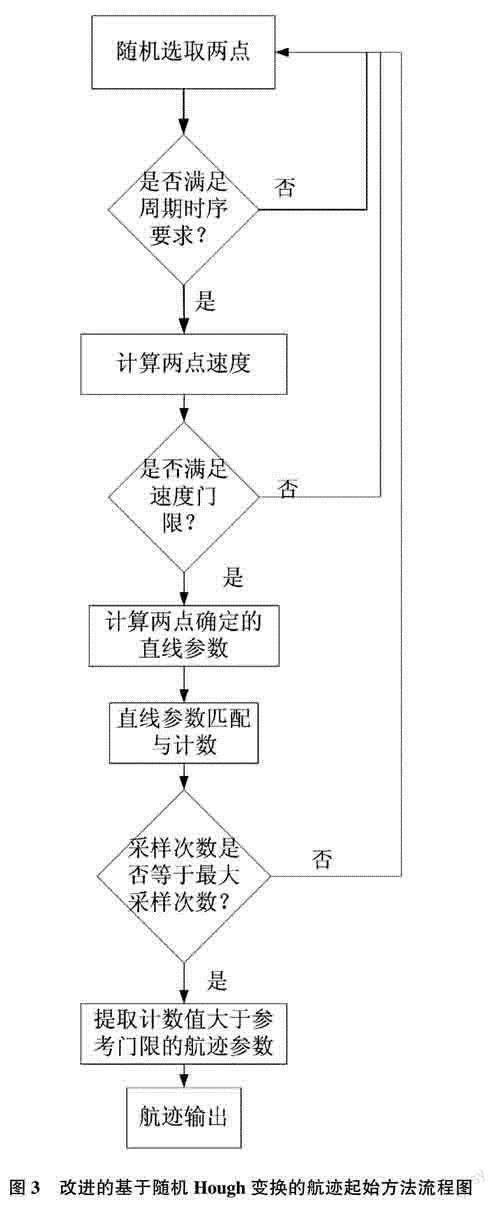
为更好地应对目标截获概率低、回波不连续的问题，本文提出一种三维空间中基于随机Hough变换的新的航迹起始的方法。该方法考虑雷达扫描周期，对满足一定时序条件的点进行采样，以减少强杂波环境下的虚假航迹，并最大限度地降低目标回波不连续的影响；其次利用速度选通，以减少计算量，也能避免同一周期扫描下的杂波点形成虚假航迹。该算法流程图如图3所示。

从该方法的算法描述和流程图可看出，该方法可设置允许关联的日寸序差值ST，不局限于相邻周期，而是对满足时序差值ST条件的两次扫描周期内数据均可进行关联，在强杂波环境和低截获概率下也能正确起始航迹，且通过周期时序筛选和距离选通，可大大减小计算量。

4仿真验证

为了更直观地对比各个航迹起始算法的性能，在同一环境下对各航迹起始算法进行仿真比较。仿真条件为假定4个目标做匀速直线运动，使用一个3-D雷达对这些目标进行跟踪，4个目标的初始位置为（55000 m，10000 m，2 000 m） ，（45000 m，45000m，2000m） ，（35000 m，35000 m，6000m） ，（45000m，25000m，8000m），4个目标的速度分别为（500m/s，500m/s，0 m/s），（500m/s， 200m/s，0m/s），（500m/s，0m/s，0m/s），（500m/s，0m/s，0m/s），假定雷達的采样周期为Ss，雷达的量测误差体现在x，y，x轴上．均为均值为0，标准差为50m的随机误差。每个周期内的杂波个数的确定方法为：首先在（0，1）区间上产生均匀分布的随机数r，给定参数人，由式（4）确定杂波个数。

比较图5～图7可知，在有目标截获丢失，且连续截获次数少于3次时，基于修正的Hough变换和基于随机Hough变换的航迹起始方法均无法成功起始航迹。本文提出的航迹起始方法成功起始了四条航迹，这是因为该方法考虑了雷达扫描时序，并满足周期条件的点，均可进行随机采样，即使在目标回波不连续的情况下，也可最大限度地利用已检测到的点迹，在频繁丢失目标量测数据的情况下体现其良好的性能。

5结束语

基于强杂波环境和低概率截获，现有方法均无法高效、准确地进行航迹起始的背景，本文提出了一种改进的基于随机Hough变换的航迹起始方法，该方法加入速度选通条件、考虑雷达扫描周期，通过仿真分析，与现有方法相比，本文提出的航迹起始方法适用于强杂波环境和低截获概率下的航迹起始问题。