数学组合计数的基本原则与方法

苏州工业园区星洋学校(215000) 何杰

组合计数是研究满足一定条件的安排方式的数目及其计算问题,这是组合数学中重要的研究方向.在现实生活中处处存在着离散结构问题,这就决定组合计数的多样性与丰富性.组合计数也是高中数学教学的重要组成部分之一,这类问题没有一个固定的解题模式可以遵循,经常会出现一题多解的情况,这就需要具体问题具体分析.因此,当我们遇到组合计数问题时不能盲目套用公式,必须抓住本质,具体分析问题.

一、组合计数基本原则

(一)相等原则

相等原则设A,B是两个有限集,如果存在A到B上的一个一一对应映射(即双射),则A的基数等于B的基数.

注意1.相等原理中“A的基数等于B的基数”可以改成“|A|=|B|”;

2.一般使用范围:当直接去求一个集合元素的个数较为困难时,可以考虑采用相等原则,进行模式的转换,或许会产生一种“柳暗花明又一村”的效果.

例1现有100 个篮球队进行比赛,直至角逐出冠军,比赛规则是单淘汰制(即每场比赛输的一方淘汰,胜者进入下一轮,不存在平局的情况),则需要打多少场比赛才能产生冠军?

分析许多人会以这样思考方式来处理问题:

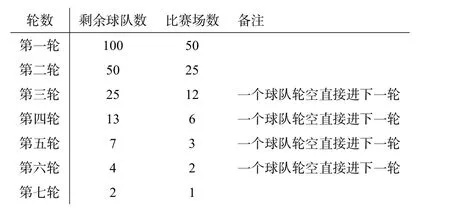
图20

这样就可以求出总计共进行50+25+12+6+3+2+1=99 场比赛才角逐出冠军.这种解法虽然很直接,但要分析每一轮比赛的情况,较为麻烦.下面可以利用相等原理给出一个巧妙的方法,我们知道每一场比赛都会淘汰一个队,比赛一场淘汰一个队,两场淘汰两个队,可知比赛的场次与淘汰的队的个数是一一对应的.

解设A={全部的比赛},B={被淘汰的篮球队},作出由A到B的映射f如下:设a ∈A,如果在a比赛中b队被淘汰,则f(a)=b,自然b ∈B.很显然f是A到B的一一映射.现有100 个队,需要淘汰99 个队,由相等原则知比赛99 场.

引申现有n个篮球队进行比赛,直至角逐出冠军,比赛规则是单淘汰制(即每场比赛输的一方淘汰,胜者进入下一轮,不存在平局的情况),则需要打n−1 场比赛才能产生冠军.

(二)加法原则

定义令S是给定的非空集合,A={S1,S2,...,Sn},其中Si⊆ S,i=1,2,...,n,若满足:(1)i=1,2,...n;(2)Si∩Sj=∅(i ̸=j);则称A为集合S的划分,其中S1,S2,...,Sn称为该划分的部分.

加法原则设A={S1,S2,...Sn}是S的一个划分,则|S|=|S1|+|S2|+···|Sn|.

注意1.加法原则还可以用初等方式表述为:完成一件事情可以分为n类,第1 类有n1种方法,第2 类有n2种方法,如此类推,第n类有nn种方法,则不同方法的总数为N=n1+n2+···+nn;

2.定义的Si中可以允许一部分是空集;

3.一般使用范围:当直接去求某个问题较为复杂,但是这个问题的所有可能情况能够被分为几个互相排斥的部分,并且要求这些部分相对易求且数目不太多时,可以采用加法原则处理问题,即关键之处是如何将集合S划分成“易于求的不太多的部分”.有时使用加法原则会产生一种“大事化小,小事化了”的效果.

例2在正方体的8 个顶点,12 条棱的中点,6 个面的中心及正方体的中心共27 个点中,共线的三点组的个数是多少?

分析刚看到这个问题或许感觉情况很复杂,无从下手.静下心来,只要确定了这三点中的两个端点,那么中间的点就自然而然被唯一确定.现在任取一个位置的一个点,比如,取正方体的上面的面中心来研究,那么三点组的另外一个端点尝试后发现只能是面中心点.同理,其它情况类似,于是我们可以分为3 种情况考虑.

解法根据题意,设S是所有共线三点组的集合,Si是第i种情况的集合(i=1,2,3):

(2)共线三点组的两个端点都是面的中心,共|S2|=3 个;

(3)共线三点组的两个端点都是棱的中点,共|S3|=个.

显然,Si∩Sj=∅(i ̸=j),所以根据加法原则满足要求的共线三点组有|S|=|S1|+|S2|+|S3|=28+3+18=49(个).

(三)乘法原则

乘法原则己知做一件事情要依次经过k个步骤,且在己完成前面i−1(1 ≤i≤k)个步骤的情况下,完成第i个步骤有ni种方法,则做这件事情的方法共有种.

注意1.乘法原则还可以用初等方式表述为:乘法原理是指做一件事情要分k步,第1 步有n1种方法,第2 步有n2种方法,如此下去,第k步有nk种方法,则做这件事方法有N=n1·n2···nk种;

2.一般使用范围:如果一件事情可以较为明确地分成几个步骤,可以一步一步完成且各个步骤要求相互独立且必不可少,这时可以使用乘法原则.使用的关键在于能够梳理出各个步骤,有时使用乘法原则会产生一种“居高临下,统筹全局”的效果.

例3用1,1,2,2,2,3,3,3,3 这九个数宇可以组成多少个不同的九位数?

分析首先观察下所给的9 个数字,可以分为3 组,分别是2 个1,3 个2,4 个3,我们可以看到数字中没有0,这样就不需要考虑首位因素.我们把9 位数看成9 个空位,要求的任务就是把这9 个数字放到9 个空位上,把3 组数分为3 步,可以用乘法原理.

解法把这9 个数字放到9 个空位上,把3 组数分为三个步骤:

第2 步:把3 个2 放在剩下7 个空位其中3 个上,有种放法;

第3 步:把4 个3 放在剩下4 个空位其中4 个上,有种放法.

二、组合计数基本方法

(一)数少条件复杂优先——枚举法

例4函数f:{1,2,3} → {1,2},设f(x)满足f(f(x))=f(x),则这样的函数共有多少个?

分析这个问题是在明确条件下构造的一个新函数,属于离散的性质,如果考虑直接计算求解相对麻烦,而且可能的情况不多,故可以用枚举法.

解法利用枚举法,作出如下表格:

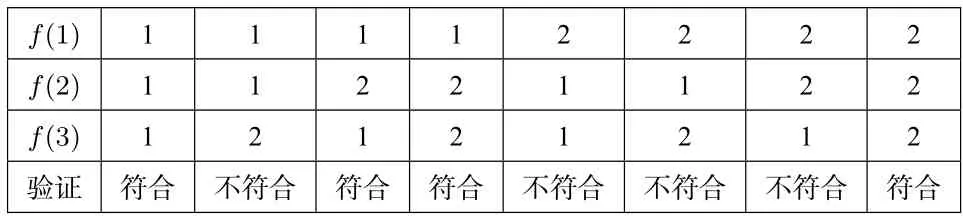
f(1)1 1 1 1 2 2 2 2f(2)1 1 2 2 1 1 2 2f(3)1 2 1 2 1 2 1 2验证符合不符合符合符合不符合不符合不符合符合

所以,这样的函数共有4 个.

枚举法适用情况与注意事项:计数的总数量不大,相对有限;枚举并不是毫无章法,为了避免计数的重复或遗漏,应当按照一定的方法或规律来计数.在组合计数问题中,当要求明确且计算的总数量不多,且没有便捷的计算方法时,可以采用枚举法把所有可能列举出来,并一一验证是否满足要求.

(二)正难但反易时优先—-排除法

例5一个正方体有8 个顶点,从中任取4 个顶点,可以构成多少个四面体?

分析如果从正面考虑,那么情况比较多,直接计数的话容易漏或重,那么可以从反面考虑,考虑总数中去除不能构成四面体的情况,则相对容易.

解法首先考虑总的情况数,即8 个顶点中取出4 个的方法数为:不符合要求的,即取出的4 个顶点不能构成四面体的方法数为,也就是找能够4 点共面的数量为12.所以所求为.

排除法适用情况与注意事项:总数相对容易计算;一种迂回的方式求解,所谓“正难则反”就是这个方法,一般是在直接处理不容易求或者比较麻烦,但是反面较容易.在组合计数问题中,当从正面计算所求的个数比较困难时,可以考虑使用排除法在一个较大的范围内求出个数,减去其中不符合要去的部分,剩下就是所求的部分.

(三)相邻整体问题优先——捆绑法

例6若有A、B、C、D、E五个人排队,现在要求C和D两人必须在相邻的位置,共有多少种排队方法?

分析要求C和D两人必须排在一起,可以先把C和D两个人“捆绑”,看作“一个人”为F,也即对“A,B、E、F”进行排列,再对F内部排序.

解法运用捆绑法,把C和D两个人“捆绑”为F,有再考虑F内部两个元素的顺序,即所以共有排队方法数为.

捆绑法适用情况与注意事项:处理的首要条件必须要求是相邻;运用时要特别注意这个看作整体的元素是否需要考虑内部顺序.在组合计数问题中,当要求某几个元素相邻时,从整体考虑出发,可以运用捆绑法将相邻元素作一个整体进行处理,然后再考虑该内部要素间顺序.

(四)不相邻单独时优先——插空法

例7一条马路两边有编号1,2,3,4,5,6,7,8,9 的九盏路灯,为了节约资源,可以将其中的三盏灯灭掉,但不能同时关掉相邻两盏或三盏,则不同的关灯方法有多少种?

解法如果直接解答需要分很多种情况思考,故可把六盏亮着的灯看作六个元素,每两个素之间有空,然后用不亮的三盏灯去插七个空位,不同的方法共有种方法.

插空法适用情况与注意事项:必须是要不能相邻;注意插空是一次性还是分次的.在组合计数问题中,当要求某几个元素不相邻的时候,可以先将其它元素排好,每两个之间看作有空位,现在将特定的不相邻的元素插入空位中,从而运用插空法将问题解决.

(五)相同元素分配优先——隔板法

例88 张相同的卡片放入5 个颜色不同信封中,每个信封至少有一张卡片,则不同的放法一共有多少种?

分析8 个元素相同,小组不同,每一组至少有一个这都满足插板法的条件,所以可以使用.

解法把8 个相同的卡片排成一列,再把4 个隔板插入7个间隔中,每一种插法就是一种放信封的方法,共有C47=35种放法.

插板法适用情况与注意事项:所有元素必须是相同的;分组后每一个小组至少分得一个元素;所分的组是有区别的.在组合计数问题中,插板法可以处理相同元素分配、间隔等组合问题的重要方法,具体而言,就是在n个元素的n−1 个间隔中放入a个隔板,这样就把n个元素分成了a+1 个组.

组合计数问题抽象,解法灵活,具有问题趣味性和结论优美性的特征.在教学中,教师必须把握数学精髓,从而达到教学效果的水到渠成.这样,学生的学习能力才能得到增强,数学素养才能得到提高.组合计数问题正吸引着一批又一批的爱好者去探索研究,真可谓“江山如此多娇,引无数英雄竞折腰”.