大深径比深小孔圆柱度误差评价

裴袁鑫 ，黄绍服

(1.安徽理工大学 机械工程学院, 安徽 淮南 232001；2.南京航空航天大学, 江苏省精密与微细制造技术重点实验室, 江苏 南京 210016；3.安徽理工大学 环境友好材料与职业健康研究院, 安徽 芜湖241003)

在工业和制造业乃至航空和军事领域，孔类零件的使用十分广泛，如发动机气缸体缸孔、航空发动机的气膜冷却小孔、炮管与枪管等，这些孔类零件在各自领域发挥着重要作用[1-3]。对于孔类零件，常见的加工方式有利用切削力的钻孔、利用高温熔化材料的激光钻孔、利用电化学腐蚀的电化学钻孔等。无论哪种加工方式，孔类零件加工时刀具的震动和加工热等都会直接影响孔的加工质量，因而对孔类零件的加工质量进行有效检测十分必要。

目前，常用两点法、三点法、三坐标测量法、数据采集仪连接百分表测量等方法检测孔类零件的内壁圆柱度误差。张翠翠等[4]以激光为光源，利用单缝衍射原理设计一种圆筒类零件内壁圆柱度检测系统，实现了对薄壁圆筒类零件的圆柱度综合误差评定，该系统检测结果准确、成本低，但对于直径1 mm 以下的深小孔激光无法有效射入，且由于孔内空间的限制无法进行有效观测；Shih 等[5]结合试验和有限元分析方法，综合分析工件由于热膨胀、切削力和夹紧力引起的内孔畸变，通过谐波识别圆柱度误差的谐波成分，得到精镗孔的圆柱度误差主要来源于内孔畸变中的主轴径向误差，虽找到了误差源，但无法获知孔的圆柱度误差，无法评价孔的加工质量；Sun 等[6]考虑偏心量、测头偏移量、测头尖端半径和倾斜误差建立了一种多系统误差的圆柱度测量模型，该模型可用于误差的分离和比较，尤其适用于37 mm 左右的大尺寸圆柱元件，但不适用于直径1 mm 及以下的小孔；Liu 等[7]提出了一种基于增量-单纯形算法的圆柱度误差评价方法，该方法在保证精度要求的基础上，运行效率优于传统算法，但仍未解决深小孔测量难的问题。

上述研究借助激光光源、有限元分析方法和数学模型提高了圆柱度误差的测量精度，但对于直径在1 mm 以下、深径比超过10∶1 的深小孔，由于小孔内部空间的限制，仍无法直接从小孔内部对深小孔进行测量，常规检测方法已不再适用；孔径极小，激光难以射入，且深孔中反射光线难以有效接收，间接测量方法如激光三角检测法同样不再适用。因此深小孔的测量成为难题，只有解决深小孔测量难的问题，才能获取深小孔的相关数据求解深小孔的圆柱度误差。鉴于此，提出使用超声波设备对大深径比的深小孔从外表面进行检测的方法，并借助软件和数学模型对检测结果进行评价。

1 工件加工与检测平台搭建

1.1 深小孔工件加工

实验工件直径为30 mm、长为100 mm，材料为304 不锈钢的光轴，在工件中心位置沿轴线方向加工直径为1 mm 的通孔。常规的钻孔设备在此深径比下，钻头极易折断，加工难度极大。实验中，选择特种加工中的电火花加工，利用电火花穿孔机在试件上加工出需要的深小孔。根据实验室电火花加工机床的使用说明，设置加工技术参数，如表1。

表1 电加工主要参数Tab.1 Main parameters of electrical machining

在深小孔加工过程中，选择去离子水作为工作液，一方面及时清除加工过程中产生的金属屑和炭黑等电蚀产物；另一方面去离子水可降低工作液的导电性，减小工作液对工件的电化学腐蚀，利于减小深小孔内壁的表面粗糙度，提高小孔的加工质量。所选工件及加工后的小孔样貌如图1。

图1 工件及加工后的小孔样貌Fig.1 Appearance of workpiece and machined small hole

1.2 检测平台搭建

检测平台主要由超声波脉冲发生接收器、传感器探头、示波器组成。超声波脉冲发生接收器选用的型号为Olympus Model 5800PR。根据被测工件材料特性及电火花加工出的小孔直径1.0 mm，选用V116-RM 型指尖接触式传感器探头，探头半径为3 mm、检测频率为20 MHz。选用Tektronix DPO3012 数字荧光示波器，示波器配有电脑软件，可在示波器固定波形后抓取波形数据并以图片形式记录，方便后期读取所需的波形数据。

2 数据获取与预处理

2.1 测量点标定

在工件表面用刻度尺沿轴线方向画出等分点，借用分度头夹持工件，并用台钳夹持画线笔，将笔尖定位到等分点转动分度头的摇柄，让工件转动1 周，即可完成1 个等分点的圆周画线。在每个等分点重复上述操作，即可在工件表面画出多个圆周线，每条轴向等分线和圆周线的交点即为测量点。探头在测量时须始终保证与工件表面充分接触，故在工件两端要留有一定的空间裕量，最终被选作测量的点共有11×12=132个。标定测量点的工件如图2。

图2 标定测量点的工件Fig.2 Workpiece with calibrated measuring points

2.2 深小孔测量

采用探头测量时，为排除探头与被测工件表面间的空气，使超声波能有效穿入被测工件，减少能量损失，保证超声波在被测工件中有足够的声强透射率，可在被测工件表面涂抹一层耦合剂。此外，探头在工件表面移动过程中，耦合剂还可减轻探头磨损，延长探头寿命。实验中测量11 个圆截面，每个截面12 个测量点，共132 个测量点，在抓取132 个测量点的波形后，读取每个测量点的时间数据tij(第i个截面上第j个测量点)，如表2。

表2 各测量点的时间数据Tab.2 Time data of each measurement point

2.3 测量数据坐标化

本实验中，将深小孔视作工件的内部缺陷，利用超声检测设备从工件外表面进行测量，测得的数据是超声波从工件外表面到深小孔内表面再反射回的时间数据，并不能直接使用，需对测得的时间数据进行处理，将其转换为空间坐标数据[8]。如图3 所示，以深孔中轴线为z轴建立空间直角坐标系。

在空间坐标系中，每个测量点的z值已知，每个测量点的x，y可借助每个测量点的时间数据计算出。光轴工件半径也已知(15 mm)，通过计算半径与厚度的差值即为每个被测点对应的深小孔内壁到中心轴的距离，再通过该距离与x，y轴之间的角度关系，借助三角函数即可得出每个被测点对应的深小孔内壁坐标，计算公式为：

其中：v为超声波在被测工件中的声速；r0为共建半径，可借助第一个测量截面进行计算。

其中：d为被测工件的厚度；t为第一测量截面平均时间；r′为深小孔半径。通过式(1)～(3)将所有的时间数据转化为坐标数据，结果如表3。

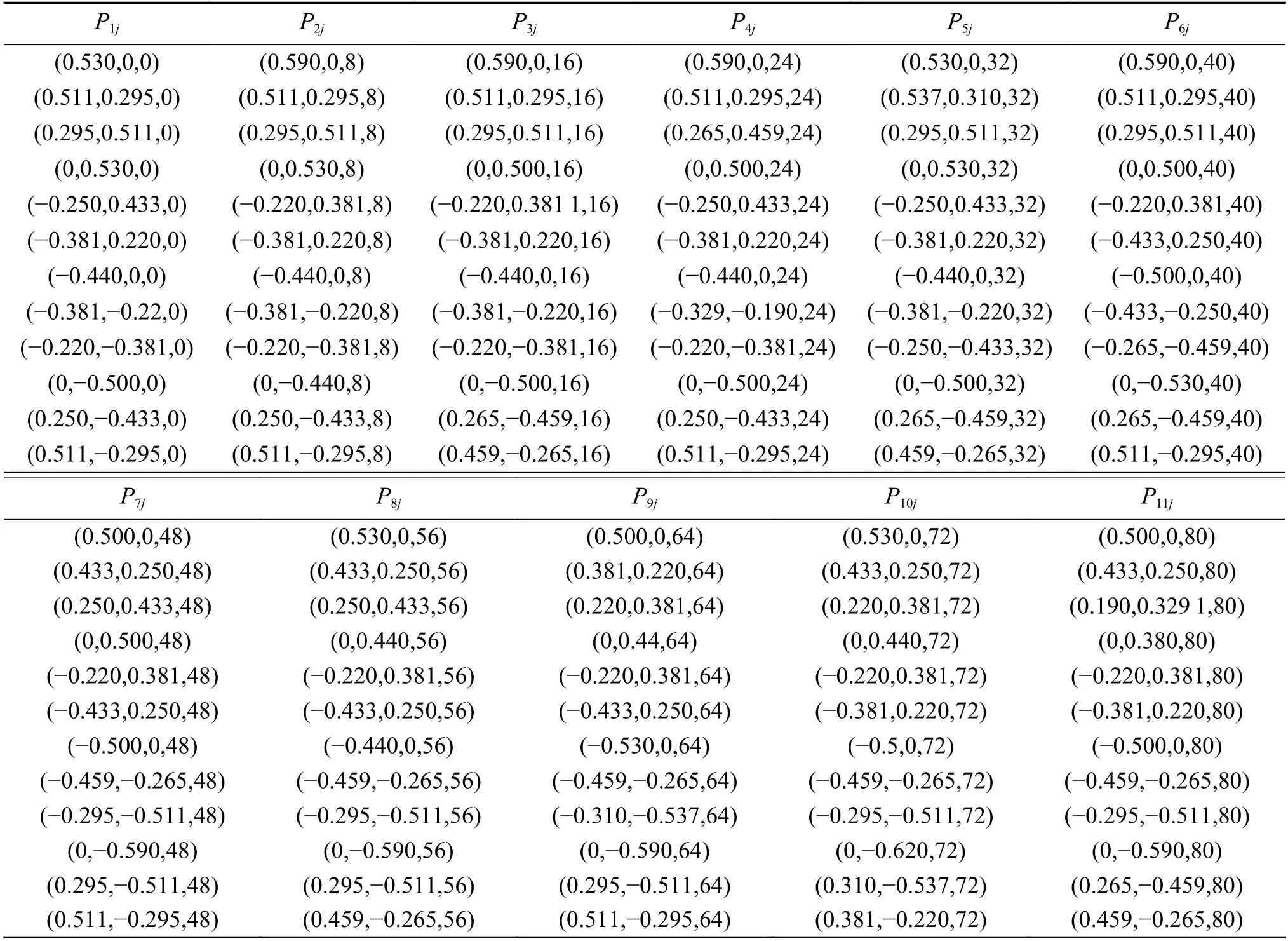
表3 各测量点坐标 单位：mmTab.3 Coordinate of each measurement point Unit: mm

3 基于遗传算法优化的圆柱度误差评价

3.1 圆柱度误差评价数学模型

圆柱度误差是被测工件实际圆柱面与其理想圆柱面之间的变动量。一个工件的实际圆柱面是固定的，但理想圆柱面是可以选取的。理想圆柱面的选取应遵循误差最小的原则，即选取理想圆柱面与实际圆柱面之间的最大变动量，再从所有的最大变动量中选取最小值。根据理想圆柱面的选取位置不同，圆柱度误差的评价方法总体上可分为4 种：最大内接圆柱法(maximum inscribed cylinder，MIC)，最小外接圆柱法(minimum circumscribed cylinder，MCC)，最小二 乘法(least square cylinder，LSC)和 最 小 区 域 法(minimum none cylinder，MZC)[9-10]。

如图4 所示，设L为理想圆柱轴线、S为实际圆柱面、M为理想圆柱面、e为圆柱度误差，则理想轴线L的数学方程为

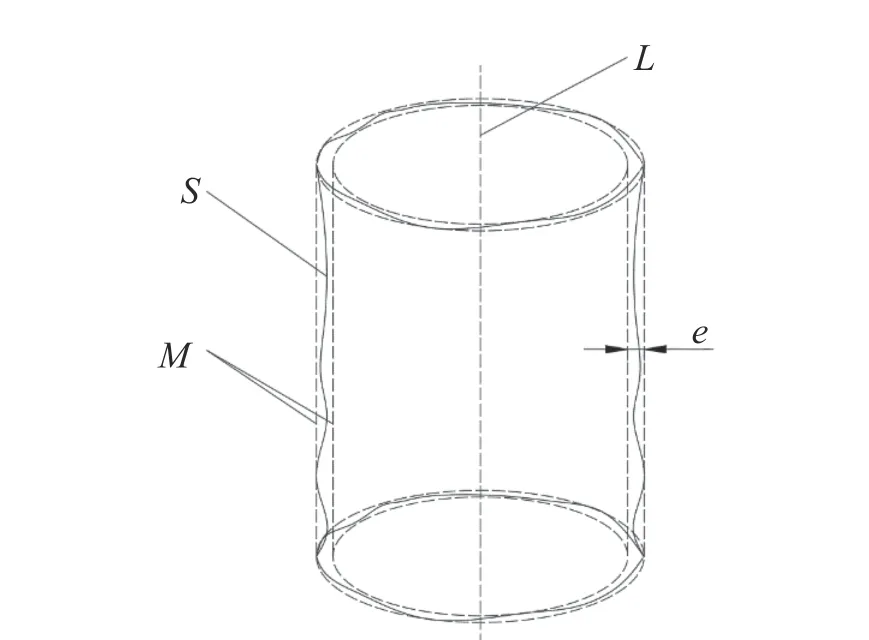
图4 圆柱度误差评价模型Fig.4 Cylindricity error evaluation model

其中a，b，u，q为理想轴线L数学方程的参数。L的方向由参数u，q决定，位置由参数a，b决定，可将理想圆柱面与实际圆柱面之间的变动量转化为理想轴线与实际圆柱面之间的变动量。在实际圆柱面M上任取k个点，设每点的坐标Mk(xk，yk，zk)，k=1，2，3，···，K，则每点到理想轴线L的距离rk可表示为：

3.1.1 最大内接圆柱法

最大内接圆柱法指在实际圆柱面内部寻找一个理想圆柱面，使理想圆柱面内切于实际圆柱面，且理想圆柱面半径最大，即实际圆柱面与理想圆柱面之间的误差最小，其寻优目标函f(a,b,u,q)=-max{minrk}，当a，b，u，q寻得最优值时，目标函数取得最小值。

3.1.2 最小外接圆柱法

与最大内接圆柱法相似，最小外接圆柱法是在实际圆柱面外部寻找一个理想圆柱面，使其外接于实际圆柱面，且最大直径为所有理想外接圆柱中的最小值。对应的圆柱度误差为被测实际圆柱面到理想圆柱回转轴线最大与最小距离的差值，其目标函数为f(a,b,u,q)=min{maxrk}，当a，b，u，q寻得最优值时，目标函数取得最小值。

3.1.3 最小二乘法

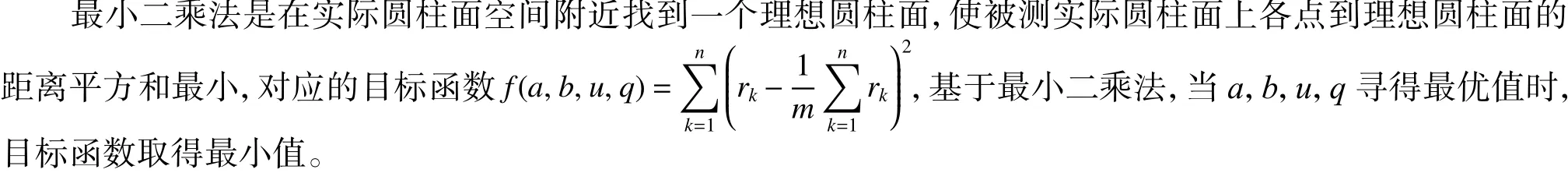
3.1.4 最小区域法

在圆柱度误差评价中，当最终计算结果有争议时，以最小区域法的结果为准，最小区域法求解得到的结果也是4 种评价方法中误差最小的。最小区域法评价圆柱度误差，实质上是寻找2 个共轴的理想圆柱面，当2 个共轴的理想圆柱面能包容实际圆柱面，且2 个理想圆柱面的半径差值最小时，其半径差即是最小区域圆柱度误差。根据定义，最小区域圆柱法的目标函数f(a,b,u,q)=maxrk-minrf，其中k，f=1，2，···，N，N为实际圆柱面上选取观测点的个数。根据最小区域法的目标函数，优化a，b，u，q使f(a,b,u,q)取得最小值，即为最小区域法的圆柱度误差。

3.2 遗传算法设置

遗传算法(genetic algorithm，GA)是根据达尔文生物进化论中的自然选择和遗传学机理，模拟自然界生物进化机制，通过将实际问题转化为数学模型，借助计算机模拟生物进化中染色体基因的交叉、变异等过程，对数学模型进行仿真运算，实现优胜劣汰的进化过程，即在寻优过程中保留有用数据，去除无用数据。GA在求解寻优问题，尤其是较复杂的组合优化问题时，通常能够较快地获得较好的优化结果[11-13]。圆柱度误差评价的4 个数学模型本质上是在实际圆柱面所在的空间寻找一个理想圆柱面，使实际圆柱面上选取的观测点到评价模型对应理想圆柱面的误差最小，从数学角度就是搜寻最优组合的a，b，u，q参数值，使f(a,b,u,q)最小[14]。故在圆柱度误差评价模型中，引入GA 以增强求解过程中模型的搜索能力，提高求解精度，即在实际圆柱面所在空间搜寻理想圆柱面，并求解出最优理想圆柱面对应的圆柱度误差值。

3.2.1 编码

GA 中主要有二进制和实数2 种编码方式，二进制编码需对待求的问题进行编码，且需根据精度要求确定字符长度，还需对求解出的结果进行解码，过程复杂，且随着编码长度的增加寻优速度会降低。为减少计算量，提升计算速度，文中选择便捷且直观的实数编码。设由4 个寻优变量(a，b，u，q)组成的第m个染色体Um=(am，bm，um，qm)。

3.2.2 适应度函数

生物进化论中，某个体对环境的适应能力即为适应度，适应度也表示研究的对象或个体繁殖后代的能力，GA 中将其称为评价函数。在进行仿真运算时，评价函数主要用于判断设置的种群中每个被选择个体的优劣程度，且是根据所求问题的目标函数进行评估的，所以适应度一般是非负值[15]。文中求解的是最小值问题，故适应度函数设置为F(a,b,u,q)=-f(a,b,u,q)。

3.2.3 遗传算子

选择操作使用系统默认，为均匀随机选择；交叉和变异操作同样使用系统默认，MATLAB 软件自带的GA 与直接搜索工具箱(GADS)会根据问题建立与结果板块( problem setup and results )中输入的约束类型选择变异函数；GA 的计算精度受初始种群数及迭代数的影响非常大。故设种群数为500、交叉概率为0.8、变异概率为0.1、最大迭代数500，最大迭代数也是遗传算法的终止条件。

3.3 误差求解

将处理后得到的坐标数据(表3)导入MATLAB，先进行三次样条插值处理[16]，丰富计算的坐标点数，再借助经GA 优化的数学模型，分别对最大内接圆柱法、最小外接圆柱法、最小二乘法和最小区域法评价模型求解。GA 搜索计算时随机选取样本点，故每次求解结果均不相同。为进一步提高结果的精度，每个评价模型计算10 次，取10 次结果的平均值作为误差求解的结果。最终求解的a,b,u,q及各评价模型对应的圆柱度误差结果如表4。

表4 误差求解结果Tab.4 Error solving results

由表4 可看出：借助GA 优化的数学模型均可搜索出对应的最优理想圆柱轴线，并可求解出对应的圆柱度误差；最小区域法求解得到的误差最小，为0.142 mm，优于最大内接圆柱法、最小外接圆柱法和最小二乘法，符合圆柱度误差评价中最小区域法误差值最小的准则[17]。

4 结 论

针对直径在1 mm 以下、深径比超过10∶1 的大深径比深小孔检测难的问题，提出一种利用超声波设备检测的方法。将加工后的深小孔视作工件的内部缺陷，从工件外表面利用超声检测平台对深小孔进行测量获取原始声程数据；将获取的原始数据通过坐标化处理，导入GA 优化的最大内接圆柱法、最小外接圆柱法、最小二乘法和最小区域法的数学模型中，搜寻最佳理想轴线，求解圆柱度误差。结果表明：提出的检测方法可完成大深径比深小孔的检测；借助GA 优化的圆柱度误差数学模型均可搜索出对应的最优理想圆柱轴线，求解出对应的圆柱度误差，且符合最小区域法误差最小的准则，证明了利用超声设备检测深小孔的可行性。本文研究可为大深径比的深小孔检测及其评价提供一种可行的方案。