基于前馈-反馈的变权重路径跟踪控制方法
2023-05-08蒋潇杰
韦 峻 江 洪 蒋潇杰 姜 民
1(江苏大学汽车与交通工程学院 江苏 镇江 212013) 2(江苏大学机械工程学院 江苏 镇江 212013)
0 引 言
近年来,随着计算机、传感器和通信技术的发展,无人驾驶车辆已成为车辆工程领域的研究前沿和工程应用领域的落地方向[1-2],同时,无人驾驶技术作为能有效提升交通安全的有力手段,成为了各高校及科研机构的研究重点。
对于无人驾驶技术,路径跟踪控制是重要的一环,路径跟踪控制是指在车辆运动学/动力学微分方程的基础上,通过对车辆前轮转角、油门踏板和制动踏板的控制实现对期望路径的跟踪[3],目前,国内外学者分别使用PID控制[4]、滑膜控制[5]、鲁棒控制[6]、纯追踪控制[7]、LQR控制[8]及模型预测控制[9]等控制算法对路径跟踪进行研究。
目前,针对纯追踪算法在对曲率变化较大的参考路径进行跟踪时存在较大偏差的问题,有学者提出一种基于前馈和反馈相结合的路径跟踪算法。前馈控制基于纯追踪模型计算前轮转角,反馈控制基于后轮反馈控制算法计算前轮转角,通过横向误差和航向误差确定比例因子,依据比例因子进行比重分配,得到最终的前轮转角控制量[10],但后轮反馈控制算法一般只适用于低速泊车场景且在曲率快速变化时超调严重,在车速提高时,后轮反馈算法的跟踪性能会大幅下降。还有学者提出一种改进的纯追踪算法,将目标点替换为当前路径切线方向上的某一点,将超前目标信息变为当前状态信息,以避免轨迹超前[11],但该方法仍然只有前馈,没有考虑到车辆当前位姿与参考路径偏差。
针对以上不足,本文提出一种中低速下均具有较好跟踪性能的基于前馈-反馈的变权重路径跟踪控制方法,以纯追踪算法进行前馈控制,前轮反馈控制算法进行反馈控制,前轮反馈控制算法相较于后轮反馈控制算法在中速及曲率快速变化的场景仍具有更好适应性,本文的路径跟踪方法为:首先搭建车辆运动学模型,之后基于车辆运动学模型和纯追踪算法及前轮反馈控制算法搭建出权重因子固定的前馈-反馈路径跟踪控制器,继而设计以路径跟踪偏差为输入,权重因子为输出的模糊控制器,与前面的前馈-反馈控制器相结合形成变权重控制器,最后再进行仿真实验,分别运用本文所建立的变权重控制器与纯追踪算法对参考路径进行跟踪,比较两者的路径跟踪性能。经过仿真验证,本文所建立的变权重控制器能更有效地改善路径跟踪效果,减小车辆路径跟踪的横向偏差和方向偏差,提高车辆的路径跟踪精度。
1 车辆运动学建模
在良好路面的中低速行驶工况下,一般不需要考虑车辆稳定性控制等动力学问题,基于运动学模型设计出的控制器也能保证对车辆底层执行层下发的指令符合车辆运动学约束[12]。车辆转向运动学模型如图1所示。

图1 车辆运动学模型
车辆的运动学模型如式(1)所示。
(1)
式中:Xr、Yr表示车辆后轮中心在全局坐标系下的横、纵坐标;φ表示车辆的横摆角;δf表示车辆的前轮转角;L表示车辆轴距;v表示车辆速度。
由车辆的后轮中心坐标可以计算前轮中心坐标,前轮中心坐标如下:
(2)
式中:Xf、Yf表示车辆前轮中心做全局坐标系下的横、纵坐标。
2 前馈-反馈路径跟踪控制
2.1 纯追踪算法
纯追踪控制算法(Pure Pursuit)是一种典型的横向控制方法,该算法进行路径跟踪时对外界的干扰具有较好的鲁棒性。其运用汽车的几何学原理,基于当前车辆后轮中心位置,在参考路径上于前视距离(自定义)lp处匹配到一个目标点,假设车辆可以按照一定的转弯半径R行驶到达该目标点,然后根据前视距离lp,转弯半径R,车辆坐标系下目标点的朝向角α之间的几何关系来确定车辆的前轮转角。图2为算法的原理示意图,由图中的几何关系可得到式(3)、式(4)。
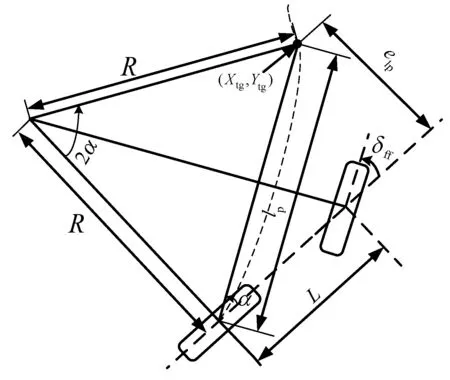
图2 纯追踪算法示意图
lp/sin(2α)=R/sin((π/2)-α)
(3)
sinα=elp/lp
(4)
根据阿克曼转向几何,可以推出式(5)。
δff=tan-1(L/R)
(5)
将式(3)、式(4)代入式(5),则推出式(6)。
(6)
式中:lp表示车辆的前视距离;α表示车身与目标点的夹角;elp表示车辆当前姿态和目标点在横向上的偏差;R表示车辆的转弯半径;δff表示采用纯追踪控制算法进行路径跟踪时求得的车辆前轮转角。
前视距离的取值对路径跟踪的精度有着较大的影响[13]。本文中,采用的前轮反馈控制算法可降低非最优前视距离对跟踪精度产生的负面影响。因而,本文不设计复杂的前视距离自适应函数来提高路径跟踪精度。参考文献[14],设置前视距离为随车速变化的函数:
(7)
式中:v的单位为km/h。
2.2 前轮反馈控制算法
前轮反馈控制(Front Wheel Feedback Control)又被称Stanley控制,其核心思想是基于车辆前轮中心与参考路径的跟踪偏差求取前轮转角。前轮反馈控制算法的示意图如图3所示。

图3 前轮反馈控制算法示意图
其控制原理可以用式(8)来表示。
δfb=φe+tan-1(kelf/v)
(8)
式中:δfb表示运用前轮反馈控制算法进行路径跟踪时求得的前轮转角;φe表示参考路径上离车辆前轮最近点处的参考横摆角和车辆横摆角的偏差值;k表示可调节的控制增益量;elf表示参考路径上离车辆最近点和车辆的横向位置偏差值。
2.3 基于前馈-反馈的路径跟踪控制方法
对于上述两种控制算法,纯追踪算法由于设置前视距离能够适应考虑前方路径,但却不能考虑到车辆当前位姿和参考路径的偏差,且在中等车速下的跟踪性能不佳,而前轮反馈控制算法虽然考虑到了车辆位姿与参考路径的偏差,但由于没有设置前视距离进行预瞄,无法考虑到前方路径的情形,故而容易出现过度转向的情况。
本文针对中低速无人驾驶车辆对曲率变化较大的参考路径进行跟踪时存在较大跟踪偏差的问题进行研究,将纯追踪控制算法与前轮反馈控制算法相结合组成前馈-反馈控制进行路径跟踪。这样,既考虑了前方参考路径的情况,又考虑到车辆位姿与参考路径偏差对车辆跟踪性能的影响,达到改善车辆跟踪效果的作用。
前馈-反馈控制方法下的车辆前轮转角计算如式(9)所示。
δf=k1δff+k2δfb
(9)
式中:k1、k2表示权重因子,满足k1+k2=1。
3 模糊控制器设计
k1、k2表示路径跟踪系统中车辆前轮转角的权重因子,如果将该系统的中的权重因子设为定值,则难以消除外界干扰因素对跟踪结果造成的不良影响。因而,本文基于模糊控制的思想,通过设计变权重的模糊控制器来解决这个问题。
本文采用MATLAB中的模糊逻辑工具箱(Fuzzy Logic Toolbox)对权重因子k1的取值进行在线优化。由于车辆与参考路径的横向偏差和方向偏差的大小是影响路径跟踪系统跟踪精度和稳定性的重要因素,故本文将车辆与参考路径的横向偏差和方向偏差作为模糊控制的输入,权重因子k1作为模糊控制的输出,设计权重因子自适应的模糊控制规则。
首先将横向偏差和方向偏差进行归一化处理,如式(10)、式(11)所示,
(10)
(11)
式中:ey表示车辆与参考路径的横向偏差;ephi表示车辆与参考路径的方向偏差。

本文中,模糊控制规则设计的原则是使车辆在对参考路径进行跟踪时,能够将车辆的跟踪偏差限定在一定的范围内,同时也有较好平顺性。即当车辆当前的横向偏差和方向偏差较大时,为了使路径跟踪系统能够快速响应,以便于减小跟踪偏差,应该将k1取较小值,基于以上分析,设计的权重因子随归一化后的横向偏差与方向偏差变化的控制规则如表1所示。

表1 权重因子k1模糊控制规则表
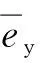
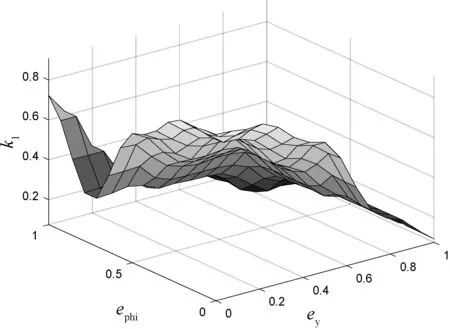
图4 权重因子模糊控制规则图
4 仿真实验
为了验证所提出改进方法的有效性,在MATLAB/Simulink环境中采用运动学模型作为车辆的路径跟踪仿真模型,采用改进前有代表性的三组固定权重因子(参数1,k1=1;参数2,k1=0.5;参数3,k1=0)模型及相关度较高的参考文献[10]所提出的方法分别与本文所提出的改进方法进行比较,为体现前两者与改进方法的差别,分别出图进行比较。本文将典型工况双移线作为参考路径,车速分别设为30 km/h、55 km/h,车辆初始位置为(0.1,0),初始横摆角设为0,改进方法中控制增益量k=0.1,文献[10]中横摆角偏差增益kth取50,横向偏差增益ke取0.6;仿真车辆参数参考某乘用车,车辆质量m=1 723 kg,前轴至质心距离a=1.232 m,后轴至质心距离b=1.468 m,绕z轴转动惯量为Iz=4 175 kg·m2,前轮侧偏刚度C1=66 900 N/rad,后轮侧偏刚度C2=62 700 N/rad。
仿真结果如图5-图12所示,其中图5-图8为车速30 km/h的仿真曲线,图9-图12为车速55 km/h的仿真曲线。为了区分本文中权重因子(参数)固定模型与引用参考文献[10]的方法,特将两者分别以(a)、(b)两部分图区分开。

(a) 改进方法与固定参数对比
(b) 改进方法与参考文献对比图5 30 km/h时路径跟踪效果对比图

(a) 改进方法与固定参数对比

(b) 改进方法与参考文献对比图6 30 km/h时车辆横向偏差对比图
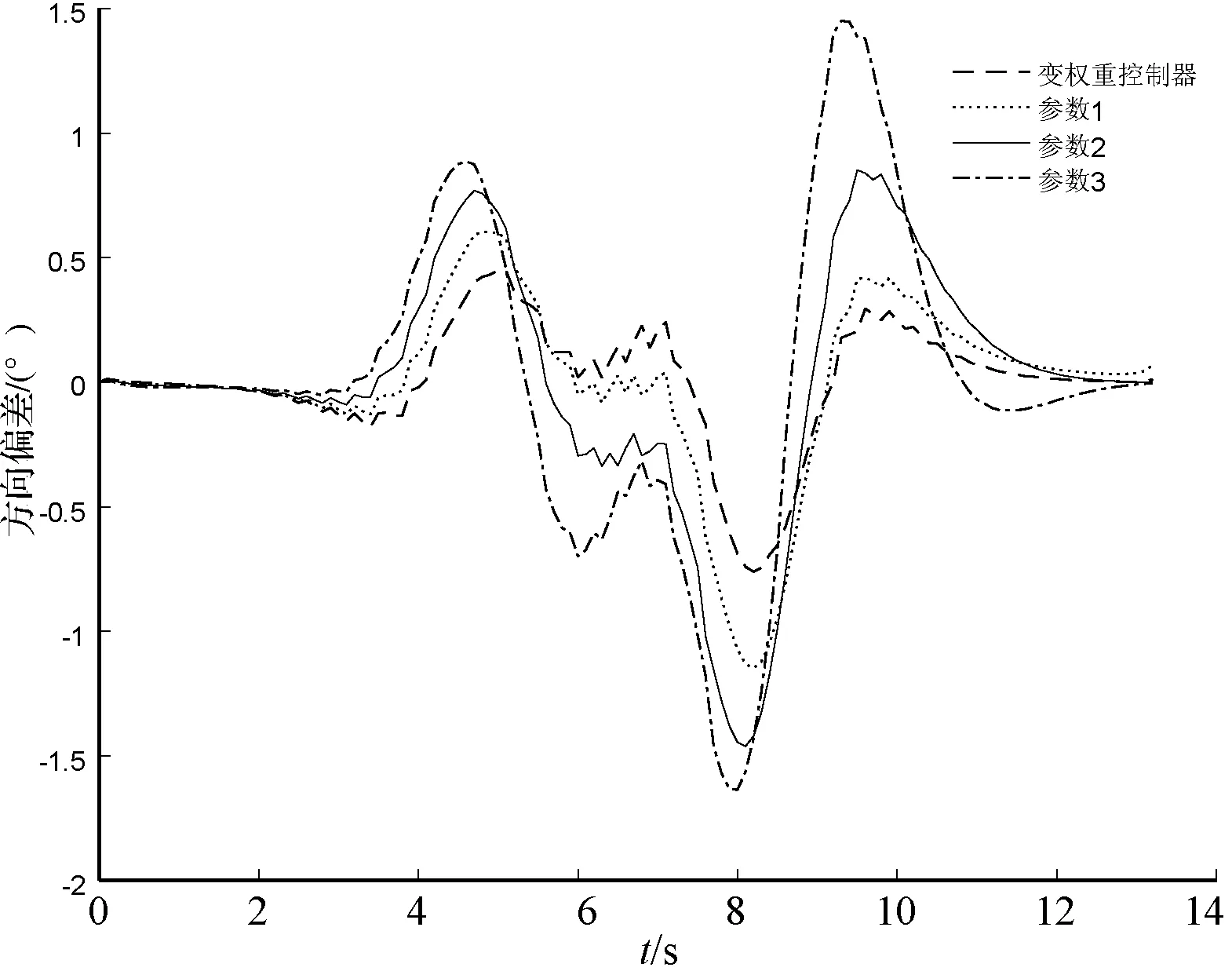
(a) 改进方法与固定参数对比
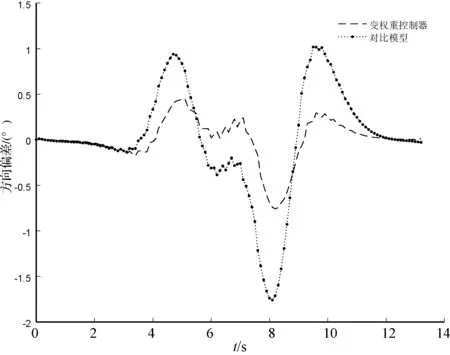
(b) 改进方法与参考文献对比图7 30 km/h时车辆方向偏差对比图

(a) 改进方法与固定参数对比
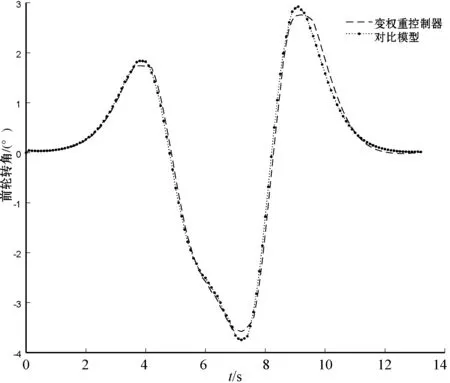
(b) 改进方法与固定参数对比图8 30 km/h时车辆前轮转角对比图

(a) 改进方法与固定参数对比

(b) 改进方法与参考文献对比图9 55 km/h时路径跟踪效果对比图

(a) 改进方法与固定参数对比
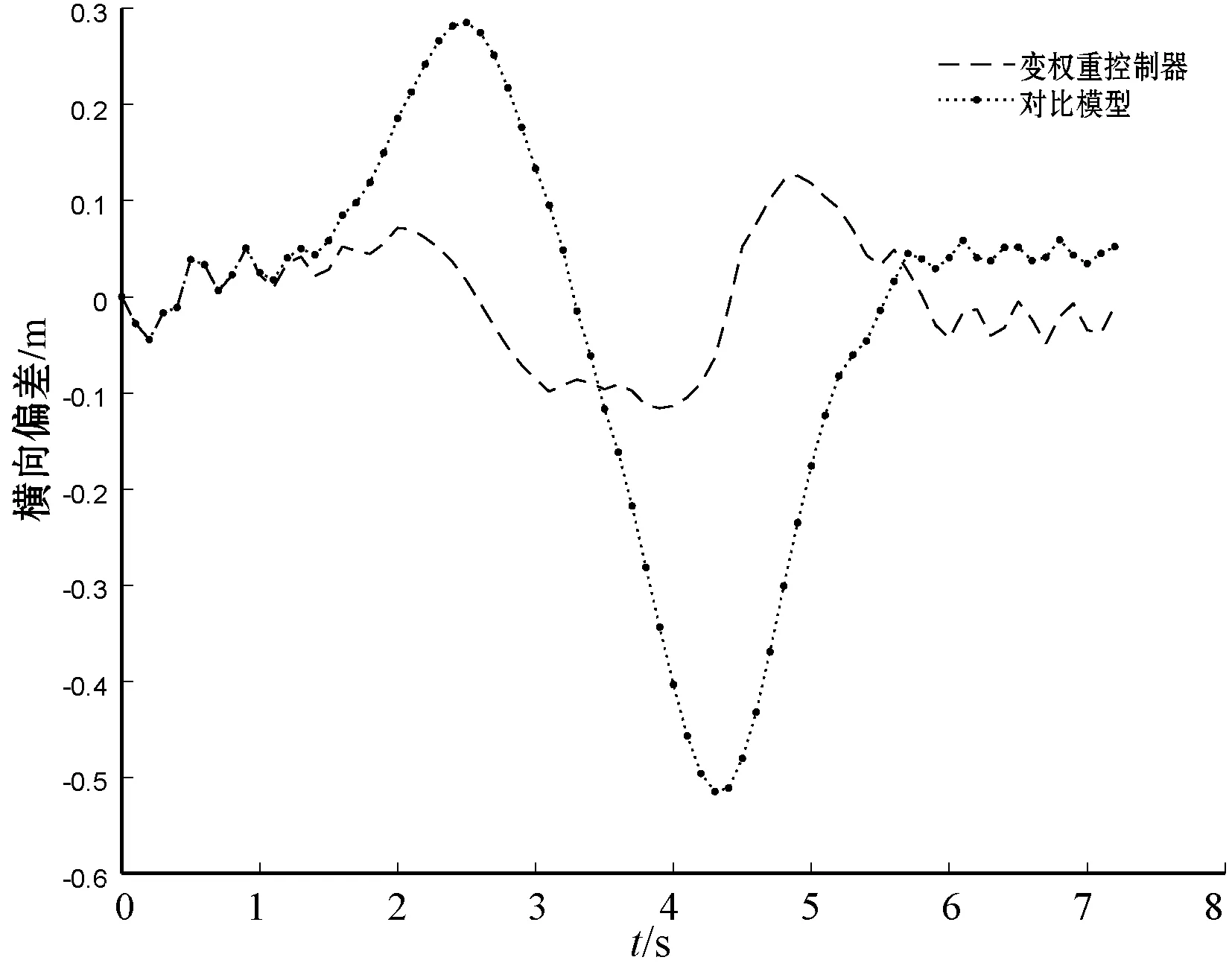
(b) 改进方法与参考文献对比图10 55 km/h时车辆横向偏差对比图

(a) 改进方法与固定参数对比

(b) 改进方法与参考文献对比图11 55 km/h时车辆方向偏差对比图

(a) 改进方法与固定参数对比

(b) 改进方法与参考文献对比图12 55 km/h时车辆前轮转角对比图
由表2可以看出,在低速情况下,变权重控制器相较于参数1、参数2、参数3对应横向偏差峰值分别优化了13%以上、16%以上、36%以上,方向偏差峰值分别优化了33%以上、47%以上,53%以上,前轮转角峰值方面只较参数1、参数2分别优化了11%和7%左右,且略高于参数3对应模型的前轮转角峰值;在中速情况下,变权重控制器相较于参数1、参数2、参数3对应横向偏差峰值分别优化了16%以上、31%以上、49%以上,方向偏差峰值分别优化了49%以上、66%以上,71%以上,前轮转角峰值方面只较参数1、参数2分别优化了8%和2%左右,且略高于参数3对应模型的前轮转角峰值;这些数据对比说明改进的方法较固定参数而言可以在保证跟踪平稳性基础上提高跟踪准确性。

表2 仿真结果峰值数据对比表
由表2可以看出,在低速情况下,本文改进方法跟踪性能略优于文献[10]中跟踪方法。在中速情况下,本文改进方法仍能较好跟踪参考路径,而文献[10]中所提方法的最大跟踪横向偏差却达到0.514 7 m,远远无法满足跟踪准确性。
由此可以看出在车辆中低速情况下,对曲率变化较大的路径进行跟踪时,本文所提出的基于前馈-反馈的变权重控制方法对参考路径有更好的跟踪精度。
5 结 语
针对中低速无人驾驶车辆在曲率变化较大路径进行跟踪的问题,提出了一种变权重路径跟踪控制器,基于纯追踪算法与前轮反馈控制算法的优势设计模糊控制器,使得模糊控制输出(权重因子)能够根据车辆跟踪横向偏差和方向偏差的变化自适应地进行调整,相较于权重因子(参数)固定的模型而言,本文改进算法能够在保证跟踪平稳性基础上提高跟踪准确性,使得车辆具有较好的跟踪性能。本文搭建了MATLAB/Simulink仿真模型,将几组权重因子(参数)固定的模型以及相关度较高的文献[10]方法与本文所设计的变权重控制器进行仿真对比,验证了变权重控制器较前两者有较好的跟踪性能。
目前的研究成果对后续的实车试验具有一定的指导作用,下一步将通过实车试验对所提出的控制方案进行验证。
