一种基于混沌天牛须搜索算法的摄像机标定方法

范山城 倪受东 张宏峰

(南京工业大学机械与动力工程学院 江苏 南京 210000)

0 引 言

在机器视觉工业检测、自动导航、三维重建等领域中,所有工作的基础是摄像机标定 。摄像机标定[1]就是通过实验和计算确定相机关于世界坐标系的内在参数和外在参数的一个过程。为此,国内外研究者们提出了诸多摄像机标定方法, 应用较为广泛的有Tsai[2]提出的Tsai两步法、Faugeras等[3]和Maybank等[4]提出自标定方法[3-4]、Zhang[5]提出的基于二维平面靶标的摄像机标定方法。其中张正友标定法因标定过程简单、易实施、成本低且标定精度较高而得到广泛应用。然而,张正友标定法在进行非线性求精时,易因初始值选取不当,导致优化过程收敛缓慢或陷入局部最小值,并且其全局搜索能力会随着标定参数增多而下降。因此 ,国内外相关研究者们将智能优化算法引入摄像机标定中,既摆脱初始值影响,又增强全局搜索能力。Xing等[6]采用遗传算法标定摄像机参数,在收敛性、精度和鲁棒性方面取得很好的效果。针对因标定图像数量少而导致摄像机标定精度不高的问题,郭彤颖等[7]提出了一种基于粒子群算法的摄像机内参数优化方法 ,该方法可以较大地提高摄像机的标定精度。为了实现摄像机的准确标定,雷阳等[8]将模拟退火算法和粒子群算法混合引入摄像机标定,起到了良好的效果。为了实现快速、准确地进行双目摄像机标定,廉小磊等[9]将粒子群算法引入进来,提高了标定精度,减少了离线标定中许多不必要的标定工作。为了解决张正友方法存在的不足,王琳霞等[10]提出了一种基于混沌粒子群(CHPSO)的双目摄像机标定方法,该方法可以获得较为精确的双目摄像机标定参数。然而这些基于智能优化算法的摄像机标定方法大都存在原理复杂、计算量大、效率低、对初始值比较敏感、鲁棒性差的问题。为了解决上述问题,提高摄像机标定的精度和效率,本文提出一种基于混沌天牛须搜索算法的摄像机标定方法。

1 摄像机非线性成像

在经典物理体系中摄像机的成像通常被当作小孔成像来研究,如图1所示,其中光心OC可以被当作是小孔,真实世界中物体上某一点P经过光心OC在像平面上投影成倒像点P′的过程可以分解为世界坐标系OW-XWYWZW、摄像机坐标系OC-XCYCZC、图像像素坐标系O1-uv、图像物理坐标系O1-xy之间三个简单的变换。变换过程如下,设点p在上述四个坐标系中的坐标分别为: (XW,YW,ZW)、(XC,YC,ZC)、(x,y)、(u′,v′)。

图1 摄像机成像模型

第一个变换是将世界坐标系下点(XW,YW,ZW)转换成摄像机坐标系下点(XC,YC,ZC)的刚体变换,如式(1)所示。

(1)

式中:R是3×3的正交旋转变换矩阵,表达了坐标轴的三种基本旋转—沿X、Y和Z轴的旋转,其矩阵元素可以用三个欧拉角α、β、θ来表示;T是三维平移向量,其向量元素可以用tx、ty、tz表示。参数R和T构成了摄像机标定外参数。

第二个变换是将摄像机坐标系下点(XC,YC,ZC) 转换成图像物理坐标系下点(x,y)的透视变换,如式(2)所示。

(2)

式中:f是摄像机焦距。

第三个变换是将图像物理坐标系下点(x,y)转换成图像像素坐标系下点(u′,v′)的仿射变换,如式(3)所示。

(3)

综合式(1)-式(3),可以得到图像像素坐标系下点P′与世界坐标系下点P之间的转换关系为:

(4)

从世界坐标系中一点P到点P对应的像素点P′(u′,v′)的转换采用的是摄像机线性成像模型(理想的小孔成像模型),但是由于摄像机本身的设计和制造误差、安装误差等,会造成摄像机存在多种非线性畸变,使得上述摄像机成像过程并不能准确地描述最终的成像关系。如图1所示,在考虑多种非线性畸变的情况下,点P对应的像平面上的点实际上是点P(u,v)。本文将主要考虑非线性畸变中的二阶径向畸变和切向畸变,如式(5)所示。

(5)

式中:(x′,y′)是引入畸变后的实际图像坐标;r2=x2+y2;k1、k2是径向畸变系数;p1、p2是切向畸变系数。结合式(1)-式(3)、式(5),可以得到点P经摄像机非线性成像模型得到的实际图像像素坐标P(u,v)。

通过分析上述摄像机非线性成像过程,可以确定摄像机待标定参数包括摄像机内参、外参、畸变系数。

2 模型建立

2.1 BAS算法原理

天牛须搜索算法是(Beetle Antennae Search,BAS)是由Jiang等[11-12]提出的一种高效的生物启发式算法,其源于对天牛觅食行为和寻找配偶行为的研究。天牛拥有一对由多种类型嗅觉细胞组成的巨大触角,当天牛觅食或寻找配偶时,它会抖动身体一侧的触角来接收气味。如果左边触角探测到的气味浓度高于右边触角,天牛就会飞向左边,反之则飞向右边。依据这一原理,天牛可以完成觅食和寻找配偶。现实中天牛的运动空间是三维的,而天牛须搜索算法需要满足任意的维度空间,因而在对天牛须搜索算法进行建模之前,必须先对天牛进行以下假设:(1) 天牛左右两须位置分布于质心两侧;(2) 天牛步长与两须之间的距离的比是个固定的常数;(3) 天牛飞到下一步后,头的朝向是随机的。

BAS建模过程如下:

(1) 在维度空间中,构造天牛须朝向随机方向向量并进行归一化处理:

(6)

式中:rand()是随机函数。

(2) 创建天牛左右两须的搜索行为,模拟天牛须的活动:

(7)

(3) 天牛须判断气味的强度进行下一步位置的更新:

(8)

式中:δt表示当迭代次数为t时天牛运动的步长;eta是(0,1]之间的常数;f()是适应度函数;xLt表示当迭代次数为t时天牛左须的位置;xRt表示当迭代次数为t时天牛右须的位置。

2.2 混沌优化算法原理

混沌是一种在自然界普遍存在的非线性现象,拥有遍历性、规律性、随机性、敏感性等独特性质。其中,混沌的遍历性性质是混沌优化算法的理论基础,其基本思想是通过将优化变量线性映射到混沌空间产生混沌序列进行遍历搜索,然后逆映射回优化变量的取值空间,使算法免于陷入局部最小值[13]。目前,用于产生混沌序列的混沌映射方程主要有Logistic映射和Tent映射,其中Tent映射产生的混沌序列易于实现、全局遍历均匀性强、对初始值不敏感且寻优效率更高[14]。因此本文选用产生混沌序列的是Tent映射。Tent映射在数学中是指一种分段的线性映射,因其函数图像类似帐篷而得名。其数学表达式如式(9)所示。

(9)

式中:Xk表示第k维度X的混沌序列;通常取b=0.5。

式(9)经贝努利移位变换后可以表示成如式(10)所示的形式。

xk+1=(2xk)mod1

(10)

Tent映射在可行解域产生混沌序列的步骤如下:

(1) 在区间(0,1)任取一个初值X0(避免X0在小周期内(0.2,0.4,0.6,0.8)),z(1)=X0,i=j=1。

(2) 利用式(10)进行迭代,生成X(i+1),i=i+1。

(3) 如果X(i)={0,0.25,0.5,0.75},或X(i)=X(i-k),k={0,1,2,3,4},则按X(i)=z(j+1)=z(j)+ε改变迭代初值,其中:ε为随机数;j=j+1。否则返回步骤2。

(4) 如果满足终止条件,则运行停止,保留x序列,否则返回步骤2。

2.3 基于混沌天牛须搜索算法的摄像机标定

天牛须搜索算法仅仅依靠天牛单个个体就可以实现对低维度函数的高速度、高质量寻优,然而对于摄像机标定这样涉及到4维度甚至28维度的搜索任务来说,其搜索效率和全局搜索能力就会下降,导致标定精度不高,而混沌优化算法具有对初始值不敏感、搜索速度快、计算精度高、全局搜索能力强的特点[15]。所以,本文将混沌搜索算法与天牛须搜索算法结合起来,用于实现高效率、高精度的摄像机标定。

图2 混沌天牛须搜索算法流程

结合摄像机非线性成像模型与混沌天牛须搜索算法,求解摄像机参数的具体步骤如下:

(1) 根据摄像机非线性成像模型确定摄像机的待标定参数:摄像机内参、畸变系数、摄像机外参。

(2) 基于张正友标定方法,使用MATLAB标定工具箱对待标定摄像机进行预标定,得出摄像机的内部参数(fx,fy,u0,v0)、畸变参数(k1,k2,p1,p2)、外部参数(R,T)。 预标定结果作为混沌天牛须算法的初始值。

(3) 初始化算法参数。设定天牛运动初始步长δ,天牛步长与天牛两须之间距离的比值常数c,最大迭代次数Tmax,混沌映射的迭代次数Tch,步长迭代因子eta。

(4) 构造平均重投影误差适应度函数f(x):

(11)

式中:N是棋盘格角点的数量;(U,V)是使用Harris亚像素角点提取方法得到的棋盘格角点实际像素坐标;(U′,V′)是使用混沌天牛须搜索算法的摄像机标定方法后得到的棋盘格角点像素坐标。

(5) 使用混沌天牛须搜索算法对标定参数进行优化求解,算法运行结束时xbest所对应的结果就是要求的摄像机标定参数。

3 实验与分析

3.1 实 验

为了验证本文方法的可行性和有效性,搭建了一个简便的摄像机标定实验平台进行实验验证,如图3所示。该实验平台包括一台CGU2-500C CMOS高清工业相机、焦距为6～12 mm的高清工业镜头、背光板光源、19×19光学玻璃材质的棋盘格标定板(棋盘方格尺寸为4 mm×4 mm)。分别从不同角度拍摄20幅棋盘格标定板图像,利用MATLAB标定工具箱进行预标定,预标定结果如表1所示,其中α、β、θ、tx、ty、tz是第一幅标定图像对应的摄像机外参。将此结果作为混沌天牛须搜索算法的初始值。

图3 摄像机标定实验平台

采用本文摄像机标定方法,使用MATLAB进行编程。通过多次实验发现,当算法初值参数值分别被设置为k=14,δ=0.008,eta=0.95,c=0.4,Tmax=300,Tch=14时,得到最小的平均重投影误差值。最终的标定结果表2所示。

表2 基于混沌天牛须搜索算法得到的摄像机标定参数

3.2 精度与鲁棒性分析

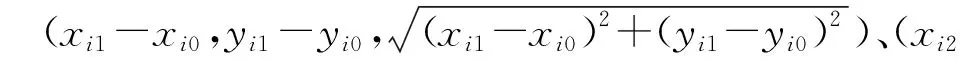
图4 平均重投影误差曲线

表3 三种摄像机标定方法性能对比

图5 反投影误差对比

为了验证本文算法的鲁棒性,在拍摄的20幅棋盘格标定板图像上分别加入均值为0,方差分别为0.1、0.2、0.3、0.4、0.5的高斯噪声,分别使用本文方法、张正友方法、基于BAS方法、基于文献[10]方法依次进行摄像机标定实验,对于每一个规定的方差值,标定结果均为50次独立实验的平均结果。以不同值的高斯噪声为x轴、相对重投影误差绝对变化率为y轴建立如图6所示的坐标系。可以较直观地发现,随着噪声的增加,四种方法的标定精度都有所下降,但本文方法的下降程度小于另外两者,即在一定的噪声变化范围内,基于混沌天牛须搜索算法的摄像机标定方法具有较好的鲁棒性。

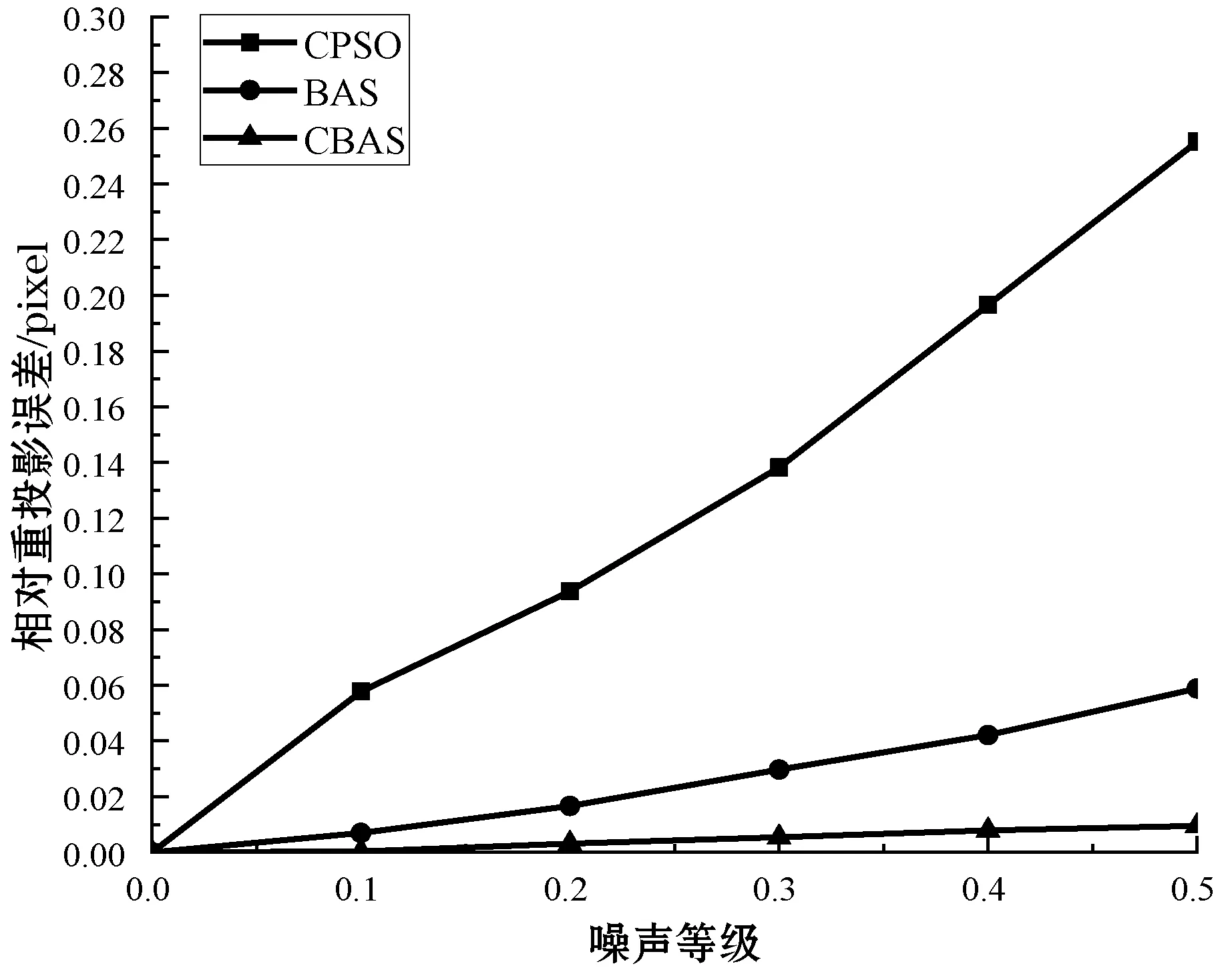
图6 不同强度噪声下标定结果的平均值

(a) 摄像机内参数、畸变参数的标准差

(b) 摄像机外参数的标准差图7 同一噪声强度下摄像机标定参数的稳定性

可以看出,随着噪声强度的增加,摄像机各参数的标准差虽有所增加但都小于0.12,即标定结果数值的离散程度不大,故本文算法具有较好的稳定性。

4 结 语

针对传统智能标定方法在进行摄像机标定时存在的对初始值敏感、精度不高、收敛速度慢且易陷入局部最优值等问题,本文提出一种基于混沌天牛须搜索算法的摄像机标定方法,其特点是在不改变天牛须搜索算法的基础上,通过增加一个基于Tent映射的混沌优化算法,使得该算法既拥有天牛须搜索算法原理简单、搜索速度快的优点,又具有混沌优化算法的全局搜索能力强、不容易陷入局部最优值的优点。最终的摄像机标定实验表明,基于混沌天牛须搜索算法可以较大地提高摄像机标定的精度和效率,具有更好的鲁棒性。下一步工作将使用本文方法进行双目立体摄像机的标定,为后续的工件三维测量奠定良好基础。