基于局部距离特征的多模态融合CNN时间序列分类
2023-05-08马志强
马志强 石 磊
1(河南农业职业学院 河南 郑州 451450) 2(郑州大学信息工程学院 河南 郑州 450001)
0 引 言
时间序列作为大数据中极其重要的一种组成,在各个领域都得到了极大的关注[1]。时间序列分类是时序分析里面非常重要的分支,即基于历史观察的序列信号对样本做出分类。由于必须考虑各个变量之间的次序关系,因此,时间序列分类问题已成为数据挖掘领域的特殊挑战之一[2-3]。
时间序列分类的难点在于保持序列的时间相关性[4]。传统的时间序列分类方法采用基于距离的方法如k-最近邻,然而,由于数据的可用性不断提升,人工神经网络已经成为模式识别的有力工具,尤其在图像数据识别方面,但是对时间序列分类中存在的可变长度以及时间扭曲问题还未能有效解决[5-6]。动态时间规整(DTW)等工具是专门为解决时间序列的困难而设计的[7]。DTW的标准用法是通过取非线性匹配时间序列元素之间的局部距离之和来计算两个时间序列模式之间的全局距离,其中元素匹配是用动态规划来完成的,它允许弹性匹配对时间失真、长度变化和速率变化具有鲁棒性[8]。然而,当使用DTW作为距离度量时,只使用全局距离,并且丢弃了有关序列元素动态匹配的信息。
将输入时间序列与原型时间序列之间的DTW匹配元素间的局部距离作为新的局部距离特征时间序列的特征。局部距离被称为局部距离特征,原始输入的时间序列是坐标特征。考虑五种不同的原型选择方法:边界法、最近法、跨越法、K-中心法和随机法[9-10]。这些方法既可用于类独立的,也可用于分类。通过从这些方法中选择的原型,可以提取局部距离特征并与CNN结合使用。但是选择哪种原型方法较优还没有一个确定的结论。
本文提出一种基于局部距离特征的多模态融合CNN时间序列分类方法,在多模融合网络中结合了局部距离特征和坐标特征,并且探索了原型选择对分类性能的影响。最后通过实例验证了本文方法的有效性。
1 基于局部距离的特征提取
1.1 使用DTW进行特征提取
DTW是一种广泛使用的算法,用于确定时间序列模式之间的距离。与线性匹配不同,DTW使用优化的元素匹配来增强对时间失真的鲁棒性,例如速率差异和时间平移。DTW确定的匹配是通过动态规划对相似元素进行对齐来完成的。具体而言,DTW通过估计由元素对之间的局部距离构成的代价矩阵上的最小路径来匹配元素。这将在时间维度上扭曲的序列元素之间创建匹配。
给定两个时间序列,前面定义的s和一个原型时间序列p=p1,p2,…,pu,…,pU,具有U个时间步数,pu∈RQ,其中Q是每个元素的维数,DTW全局距离是最佳匹配的局部距离的总和,即:
(1)
式中:(u′,t′)是匹配的索引,分别对应于p和s的原始索引u和t;M表示索引集。然后将匹配之间局部距离的总和用作离散时间序列之间的距离度量。
然而,如式(1)所示,仅使用总全局距离,而浪费了实际匹配计算。虽然这一事实对于传统的基于距离的方法来说并不重要,但有可能丢失有关比较模式之间的结构关系的信息。图1为DTW计算之间的比较,其中元素之间的局部距离可以揭示在使用DTW作为全局距离度量时通常会丢失的其他信息。图1中显示了不同原型p1、p2、p3和p4的四个示例,每个原型和样本对都有上面所示的两个模式,连接线表示通过DTW进行匹配,下面是局部距离特征序列。它们的DTW距离与普通样本s相似。使用传统的基于距离的分类方法将无法区分不同的原型,即使原型之间存在显著差异。另一方面,时间序列的匹配元素之间的局部距离保持可以利用判别信息。因此,不是使用匹配的总和,而是使用匹配元素之间的局部距离来创建序列v,或者:

(a)

(b)

(c)
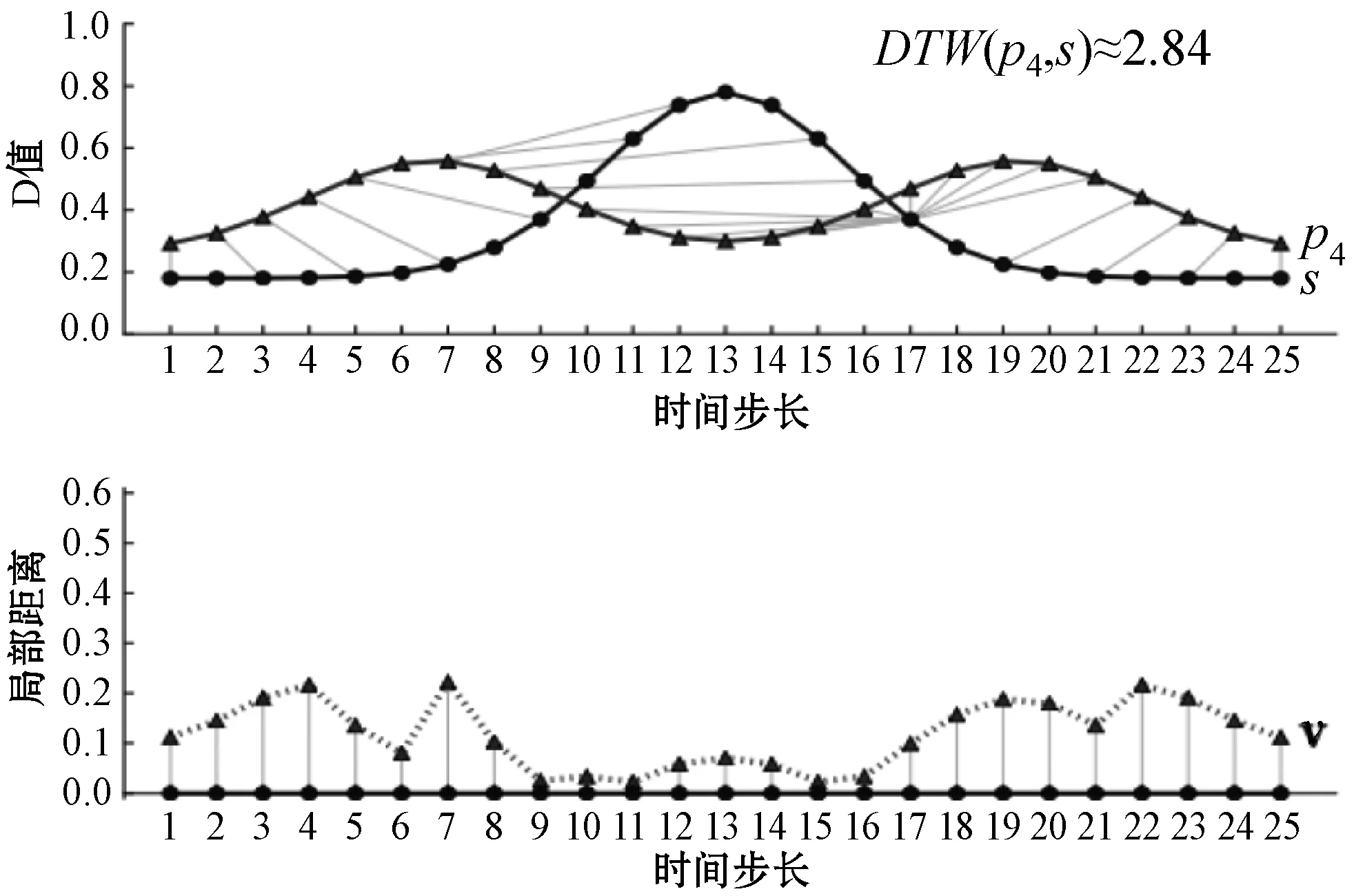
(d)图1 一维时间序列s和四个原型DTW
(2)
对于每个(u′,t′)∈M。将v的元素称为局部距离特征,将序列s的原始特征称为坐标特征。v的可视化如图2所示,其中每一列代表从样本到原型的局部距离。每行涉及一个原型p1、p2和p3,每列是一个样本s1、s2和s3的局部距离特征。基于局部距离特征的时间序列v1、v2和v3是每个样本的原型的三维组合。

图2 局部距离特征与对应的在线字符时间序列示例
当与多个原型一起使用时,一个多元序列表示为:
(3)
将创建RK中v的每个元素,其中K是原型总数。当使用DTW斜率约束时,确保时间步长相对于原型序列总是前进一个,例如由递归函数定义的非对称斜率约束:
(4)
式中:D(u,v)是累加和,只要原型长度相同,就可以使用不同长度的输入序列来创建固定长度v。这是因为使用这种特殊的斜率约束保证了M中的匹配数将始终等于原型序列p中的元素数。因此,局部距离特征序列v的表达式提供了一个固定长度、时间扭曲的时间序列。
1.2 CNN分类
在构造出局部距离特征序列后,提出将它们用作一维卷积CNN的输入,以进行时间序列分类。坐标特征表示原始时间序列模式,局部距离特征表示与原型模式的关系。通过结合这两种特征,可以训练一种结合了来自两种数据类型信息的CNN。
将两种不同的数据模式结合起来称为多模态分类。在CNN的背景下,可以通过多种方式组合这些模式。如果将具有两种模式的CNN在输入级融合,则称为数据级融合或早期融合。如果CNN在中间层之一融合,则称为特征级融合或中间融合。最后,如果在分类层之前的最后,将CNN进行融合,则它是决策级融合或后期融合。融合的时间取决于模型的作者,并且像超参数一样选择。
图3概述了三种融合方案,并结合了所提出的特征提取。如图3(a)所示,早期融合模型采用坐标特征并将其与局部距离特征组合以创建单个时间序列输入。这等效于将局部距离特征视为多元时间序列的附加维度。除了数据融合之外,CNN的结构与标准时间CNN相同。对于图3(b)中的中间融合模型,这两种模态被提供给单独的卷积层集,并在共享的全连接层之前串联在一起。每个部分都将学习与各自的模态相对应的独立卷积权重集。图3(c)中的后期融合网络的结构类似于两个不同的CNN,每个CNN具有数据模态,但是被组合作为输出层的输入。
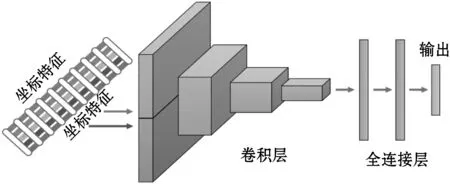
(a)
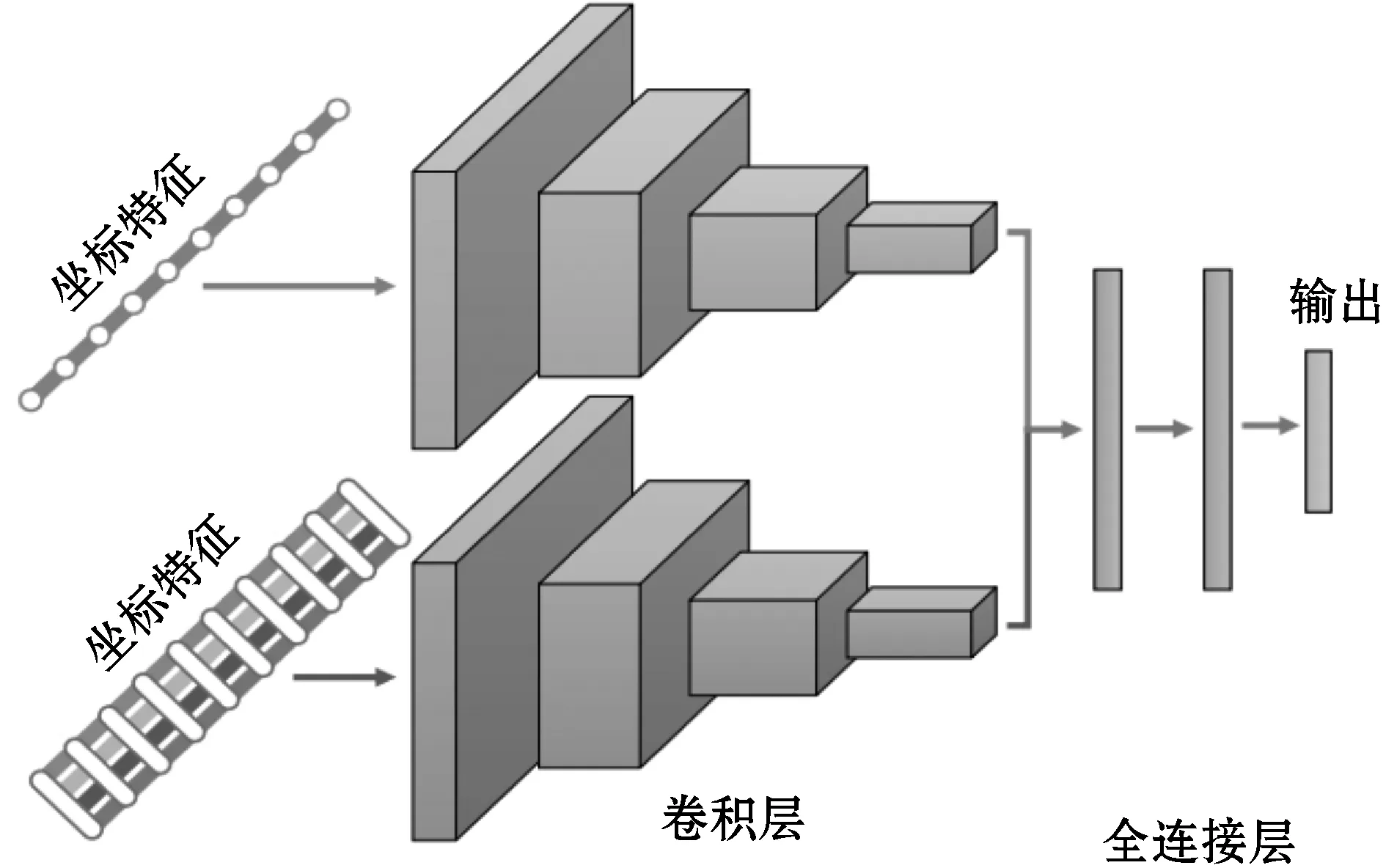
(b)
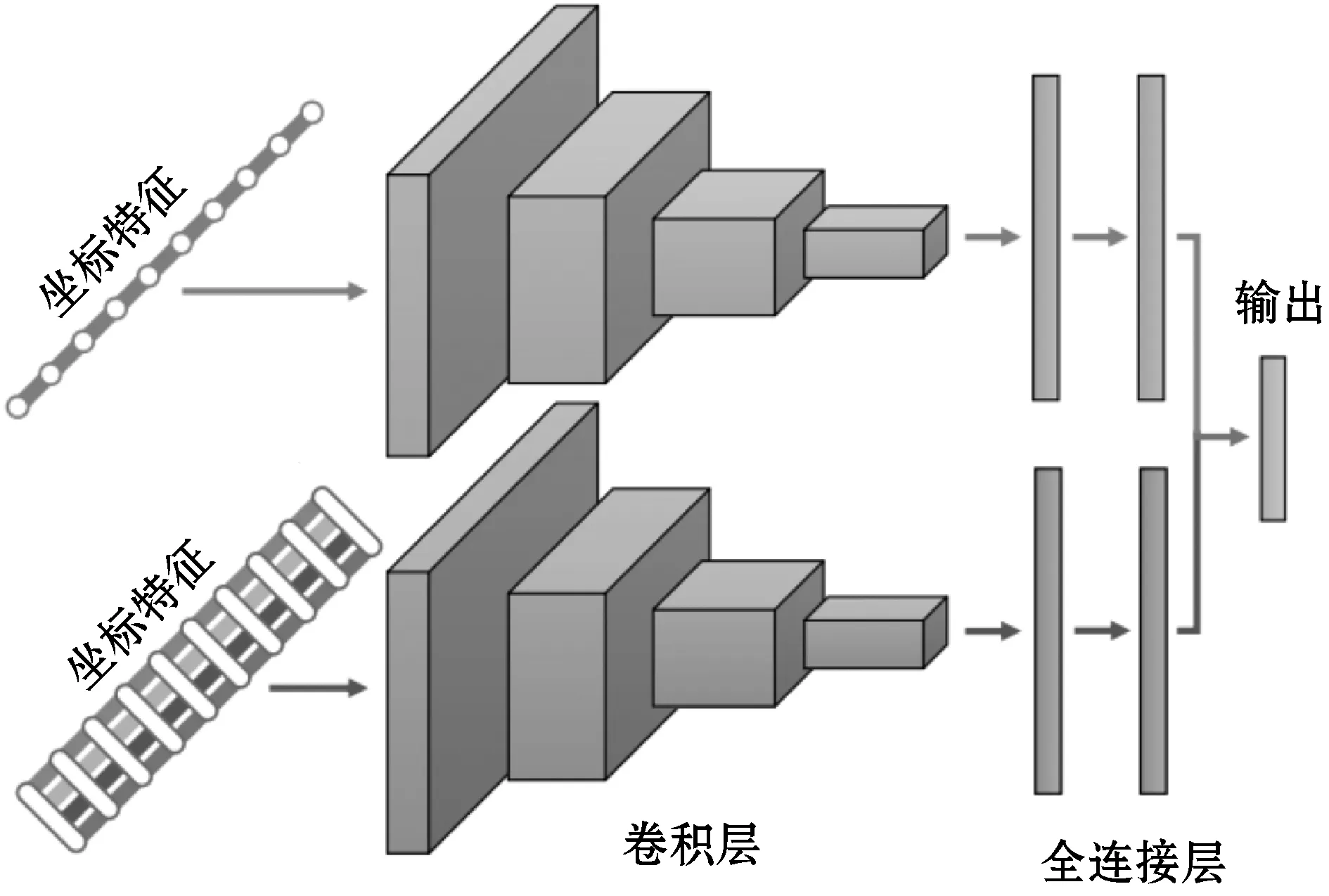
(c)图3 三种融合方案下的比较
1.3 原型选择
通过观察原型和样本之间的差异来进行基于距离的学习中的分类。但是,随着数据集规模的扩大,原型的数量可能会很大。因此,为任务选择最佳原型可能是减少计算时间同时保留准确分类所需信息的有效步骤。过去,基于距离的方法的原型选择已被广泛研究。此外,针对时间序列提出了许多原型选择和生成方法。例如,使用AdaBoost进行选择,并使用DTW重心平均进行生成。
本文借用从基于距离的分类器中选择原型的想法,以选择用于创建局部距离特征v的原型,以便有选择地增加v中嵌入的信息量。具体而言,使用随机、边界、最近、跨度和K中心原型选择从整个训练集P确定一个子集P′。这些方法中的每一个都可以在整个数据集上执行,与类无关,也可以在每个类中按类执行。除随机选择外,每一种原型选择方法均采用DTW作为距离度量进行距离计算,以适应时间序列。图4为每种与类无关的原型选择方法的示例,较大的点是原型选择方法的结果,较小的点在数字类中着色。

图4 可视化的Unipen 1a在线手写数字数据集
(1) 随机原型选择。随机选择是随机选择原型的简单方法。此方法用作故意选择方法的基准。
(2) 边界原型选择。边界方法创建一个表示训练集P边界上的模式的原型子集P′,即:
(5)
式中:Borders(P)是训练集P中原型的结果索引,该训练集具有由DTW确定的与所有其他模式的总最大距离。此过程重复K次,每次回合将选定的原型从P移到P′。当以类的方式使用时,边界原型选择方法通常会在每个类的边缘上选取模式,选择难以分类的模式或决策边界附近的模式,以类无关的方式使用时,所选模式位于整个训练数据集的边缘。
(3) 最近原型选择。“最近”采取与“边界”相反的方法。它从训练集P中最接近其他所有模式的模式构造原型子集P′。换句话说,P的中心或以式(6)的优化处理方式重复K次。
(6)
与其他方法相比,与类无关的最近选择对于本文方法来说是一种直观上较差的选择方法,这是因为所选的原型彼此相似并且几乎没有提供额外的信息。但是,当以类方式使用时,可以在选择每个类的中心原型时使用。
(4) 跨度原型选择。跨度原型选择的目的是在数据集中实现均匀分布。补充材料中概述了跨度原型选择的算法。与以前的方法不同,跨度考虑了以前选择的原型。它将选择与所有先前选择的DTW距离最远的原型。结果是一个原型集P′,它包含的原型之间的距离尽可能远,跨越整个原始数据集P。
(5) K中心原型选择。K中心原型选择方法遵循K中心或K中心点聚类方法来选择原型。选择P中的聚类的中心点的原因是为了获取一个与整个集合的分布相似的原型的分布。
补充材料中还提供了K中心原型选择算法。为了计算K中心,首先,使用跨度初始化原型集P′,以创建K中心的确定性初始化。第二,训练样本p∈P被分配到聚类C1,C2,…,Ck,…,CK,基于它们与最近的聚类中心的接近程度。最后确定每个聚类的新中心。重复这个过程,直到聚类中心没有变化。
2 实验与结果分析
2.1 数据集
Unipen 1a、Unipen 1b和Unipen 1c数据集分别由独立在线手写数字、大写字符和小写字符组成。Unipen数据集作为时间序列分类的基准已经很成熟。每个数据集包含大约13 000个模式。实验将数据集分成10份,与每个训练集中选择的原型进行10倍交叉验证。
UCI机器学习存储库是跨多个领域的大型数据集存储库。从存储库中,将四个时间序列数据集用于实验。根据以下标准选择数据集:时间序列分类任务、训练集中有足够的模式以及最新的基线。使用了来自UCI机器学习存储库的以下数据集:腕戴式加速度计数据集的日常生活活动(ADL)识别、口语阿拉伯数字数据集(Arabic)、澳大利亚手语符号数据集(Auslan)和Hill-Valley数据集。ADL由705个3轴加速度计测量组成,分为7个ADL类。Arabic包含10个口语数字类的13频率梅尔频率倒谱系数(MFCC)。该数据集有8 800个模式,其中:6 600个模式构成训练集;2 200个模式用于独立于说话人的测试集。接下来,Auslan有来自95个类的6 650个手语单词。最后,Hill-Valley数据集是由606个时间序列模式组成的综合数据集,每100个时间步长被分为“hill”或“valley”。有两种版本,一种不带噪音(HillValley),一种带噪音。如果可用,则使用具有预定义拆分的数据集的训练和测试集。当没有预定义的集合拆分时,使用10倍交叉验证。
数据集的最后一类是来自UCR时间序列分类档案的85个1D时间序列数据集。这些数据集跨越许多不同的领域并具有不同的特征。数据集具有2至60个类、60至2 709个时间步长,并且都包含预定义的训练和测试集。
2.2 实施细节
为了评估所提出的CNN局部距离特征的有效性,使用了五种实现方式:一个仅具有时间序列特征的CNN,一个仅具有局部距离特征的CNN,数据级早期融合CNN,特征级中间融合CNN和决策级后期融合CNN。所有实现都使用一维卷积层,内核大小为3,步幅为1。与通常与图像一起使用的CNN不同,时间CNN可以使用一维卷积,其中在整个时间维度上使用卷积。对于此应用,使用1D或2D卷积时结果几乎没有差异,因此选择了1D卷积方法。在每个卷积层之后,使用窗口大小为2、步幅为2的一维最大池化层。
由于第2.1节中概述的数据集范围很广,因此根据输入的长度确定卷积层和池化层的数量。具体来说,池化层的数量Lpool和卷积层的数量Lconv定义为:
Lpool=Lconv=round(log2(T))-3
(7)
式中:T是输入模式中的最大时间步数。式(7)用于确保通过最大池化将全连接层之前的最终特征长度减少到5到12个时间步长之间。使用式(7)使得实验中的模型具有2到8个卷积和池化层。至于节点数,第一个卷积层设置为64个节点,第二个卷积层设置为128个节点,并且在适用时,第三个或更高的卷积层设置为256个节点。此外,全连接层有1 024个节点,丢失率为0.5。整流线性单元(ReLU)用作隐藏层的激活函数。应当指出,还测试了其他深层神经网络如VGG,但是结果并不令人满意,也无法证明额外参数的合理性。
对于Unipen数据集,使用100个批次对模型进行了100 000次迭代训练。使用32个批次对UCI和UCR数据集进行了50 000次迭代训练。训练方案的差异是由于与其他数据集相比,Unipen数据集的大小更大。使用Adam优化器对每个模型进行了训练,初始学习率为0.000 1。
2.3 方法对比
2.3.1 Unipen在线手写数据集的评估
将Unipen数据集上的实验与文献中的9种最新方法进行了比较,包括经典方法和基于神经网络的方法[11-17]。对于经典方法,比较了基于统计DTW的隐马尔可夫模型(HMM)(HMM CSDTW)、两个SVMs(一个将DTW嵌入到高斯内核中(SVM GDTW)以及另一个使用分段多项式函数(Inter.Kernel))、在线扫描n元组分类器(OnSNT)的结果。对于神经网络方法,将本文方法的结果与DTW神经网络(DTW-NN)(该DTW神经网络将DTW集成到前馈神经网络中),使用神经网络中的笔画特征的神经模糊系统(FasArt),混合Kohonen-perceptron(KP)神经网络(Fuzzy Rep.KP),具有动态对齐权重的CNN(CNN DWA)和LSTM进行了比较。最后,展示了使用格编码和波束搜索方法的Google在线手写识别系统(Google)的结果。
2.3.2 UCI机器学习存储库数据集的评估
UCI机器学习存储库及其数据集过去有许多不同的成果,它们用专门的模型处理每个数据集。为了简洁起见,仅报告对每个数据集进行调查后发现的最新方法。对于ADL数据集,文献[17]使用CNN DWA。Arabic数据集的最新结果使用带MFCC的二阶导数(TPMFCC)的HMM。过去有很多使用Auslan数据集的作品。但是,文献中的大多数方法仅使用完整数据集的子集来限制类的数量。然而,De Rosa等在Auslan数据集的全部95个类中使用了6个方法。对于HillValley1和HillValley2,分别将本文方法与神经网络(NN)和随机位森林(RBF)进行了比较。
2.4 结果分析
表1和表2分别显示了针对Unipen和UCI数据集的五种原型选择方法的结果。补充材料中提供了UCR数据集的更详细的结果表。结果显示了在结合坐标特征和局部距离特征的中间融合CNN中使用K=5的与类无关的原型选择的准确性。根据各自的原型选择方法,本文方法被标记为“中间融合”(随机)、“中间融合”(最近)、“中间融合”(边界)、“中间融合”(跨度)和“中间融合”(K中心)。

表1 Unipen数据集的比较(%)

续表1
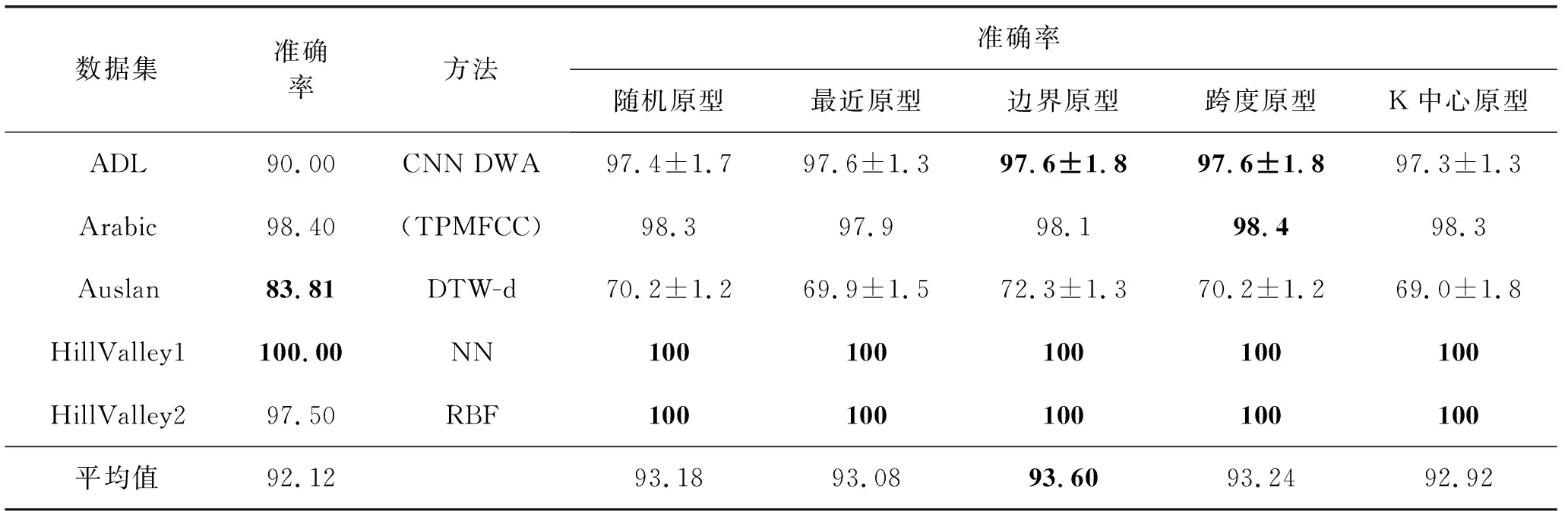
表2 UCI机器学习存储库数据集的结果(%)
表1显示了本文方法能够获得Unipen 1b和Unipen 1c数据集的最新结果,并且仅被一种经典方法OnSNT和一种现代方法Google所超越。此外,与Unipen数据集上除这两种方法以外的所有其他方法相比,所有原型选择方法均具有较高的准确性。
对于表2中UCI数据集的结果,本文方法表现异常出色。除了Auslan数据集外,本文方法具有完美或接近完美的准确度,即使为满足各自的任务而量身定制,它们还是对现有方法的最大改进。由于数据集具有95个类,每个类只有70个模式,因此Auslan数据集为深度学习提供了艰巨的任务。这证明了本文方法的弱点,因为它在小型数据集上表现不佳。
由于类似的原因,UCR数据集也很困难。大多数UCR数据集都有非常小的训练集,这对于CNN和深度学习解决方案来说通常不太理想。
3 讨 论
3.1 原型数量的影响
通过使用局部距离特征序列训练融合方法来完成实验,对于类无关和按类的原型选择。对三个Unipen数据集重复此操作,并进行10倍交叉验证。
直观地讲,原型越多,每个局部距离特征序列中嵌入的信息越多,因此可以学到的信息就越多。这个直觉由图5证实,实线代表使用各种原型选择方法的10倍交叉验证的平均值,裕度是上下的标准偏差。其中在最初的几个原型中,准确度大大提高。但是,当使用大量原型时,准确性下降得会非常严重。尽管使用了十倍的类数,即1a为100,而1b和1c为260,但准确度却几乎没有提高。因此,在选择最少数量的原型后,增加模型的计算时间和复杂性是不值得的。因此,表1和表2的结果仅使用5个原型获得,尽管能够使用更多的原型报告更高的准确度。

(a)


(b)图5 使用仅具有局部距离特征的CNN在Unipen数据集上的测试结果
3.2 原型选择方法的影响
要研究的最重要因素之一是原型选择方法之间的差异。类似于原型数量的影响,原型选择方法的准确性与所选原型的变化相关。选择数据均匀分布的方法往往比从狭窄原型中选择原型的方法更好。
(1) 类与类无关。由于图5显示,当增加原型集的大小时,在准确度上存在严重的递减回报,并且用于类选择的最小原型数量固定在类的数量上,因此与类无关的选择更适合于分析。融合网络方法的分类选择结果可以在补充材料中找到。
(2) 最近原型选择。如前所述,与类无关的“最近”是一种直观上较差的原型选择方法,这在图5(a)中得到了反映。在每个数据集中,除K=1外,最近的表现最差。K=1的一个例外是由于中心原型是数据集的平均表示。但是,由于其他原型选择方法添加了其他原型,因此失去了优势,因为最近继续从数据集中的中央区域选择原型。
(3) 边界原型选择。至于其他的原型选择方法,区别则更加微妙。天真地,边界将具有最大的变化,这是因为边界选择了式(5)中描述的距所有其他点最远的训练模式。但是,当使用度量多维缩放(MDS)和主成分分析(PCA),使用DTW作为距离度量来可视化Unipen 1a的训练集之一时,在图2中可以看到并非总是如此。图2显示,虽然选定的边界模式距离数据集中的其他点最远,但它们可以彼此相似。
(4) 跨度原型选择。跨度采取了相反的方法来寻找与边界相比最远的原型。跨度可以找到距已选择的原型最远的模式,而不是从数据集中确定最远的模式。这意味着跨度原型被选择为跨越整个训练数据集,从而导致非常不同的模式的表示。通常,图5中的结果表明,跨度是为基于局部距离特征的分类选择原型的最佳方法。
(5) K中心原型选择。类似于跨度,K中心原型选择由于使用聚类的类群而找到了良好的原型分布。但是,与直觉相反,K中心的表现通常不会优于跨度。这表明聚类的中心模式对于局部距离特征不如均匀分布数据集那样有利。
(6) 随机原型选择。尽管仅将随机选择作为其他方法的基准,但结果表明,随机选择原型往往效果很好。这种现象的一个原因是高斯分布中的随机选择模式,因此选择模式具有良好的数据集表现。对于图2中的数据集,随机和K中心的原型分布看起来大致相同,并且所有数据集的结果都反映了这一点。
3.3 融合方法的影响
影响最大的模型设计选择是融合方法的时机选择。图6为Unipen 1a、Unipen 1b和Unipen 1c数据集的临界差,用于比较融合和选择方法(其中)。平均等级是使用10倍交叉验证计算的,每个训练和测试集的每次比较均相同。在特征级融合CNN通常具有最佳效果。同样,临界差图表明,与仅使用局部距离特征时不同,使用融合网络时,原型选择方法之间没有显著差异。

图6 Unipen 1a、Unipen 1b和Unipen 1c数据集的临界差
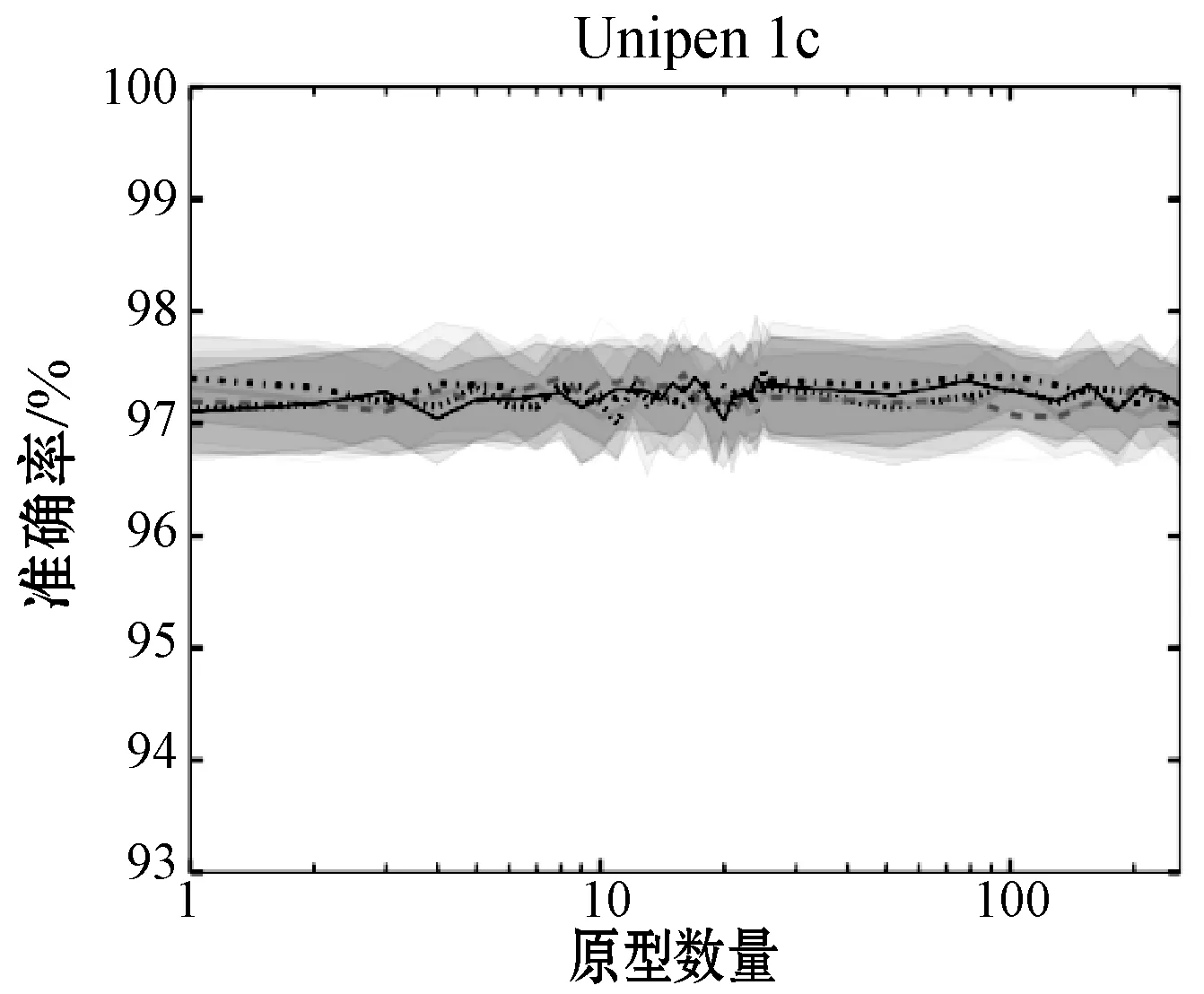
此外,在图7中,实线代表使用类无关进行的各种原型选择方法的10倍交叉验证的平均值,裕度是上下的标准偏差。可以看出,对于中后期融合网络,增加原型的数量,甚至是类数量的10倍,对准确度的影响很小。这表明即使原型数量很少,局部距离特征也仅通过坐标特征即可为多模式网络提供信息(表1)。

(a)

(b)
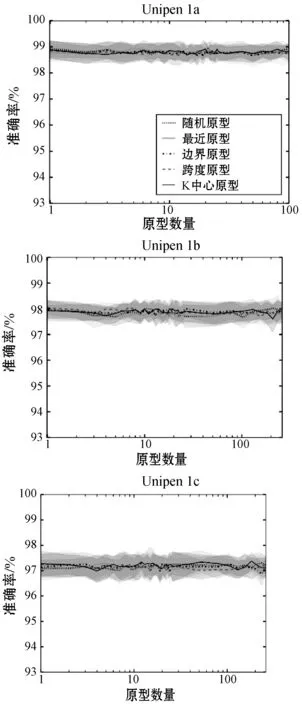
(c)图7 三种多模态融合方案的测试结果
图7(a)中的早期融合准确度图特别有趣。这三个数据集具有相似的趋势,因为它们最初具有逐渐降低的准确度,直到它们收敛于仅图5(a)的上升局部距离特征准确度。其原因是在数据级融合时数据维度的不平衡。对于Unipen数据集,原始坐标特征代表平面的两个空间维度。当K小时,两个特征的维数平衡。但是,随着K的增大,局部距离特征会掩盖甚至会干扰坐标特征,从而导致准确度下降。这是值得注意的,因为通过在CNN中稍后融合这些模态,可以通过在融合时具有平衡的特征表示来克服此问题。
此外,图7(b)、图7(c)和图6显示,原型选择方法之间只有很小的差异。临界差由Nemenyi事后检验定义,其中α=0.05,或者:
(8)

图8显示了Unipen 1b数据集(大写字符)的交叉验证折叠错误分类。每列显示了用实心圆圈表示错误分类的交叉点:分别对比单独使用坐标特征以及本文方法使用不同原型选择方法。原型选择方法之间的差异是细微的。通常,多种方法会漏掉错误分类的字符。尽管如此,图8还显示,与单独使用坐标特征相比,使用坐标特征和局部距离特征的中间融合CNN具有较少的误分类。
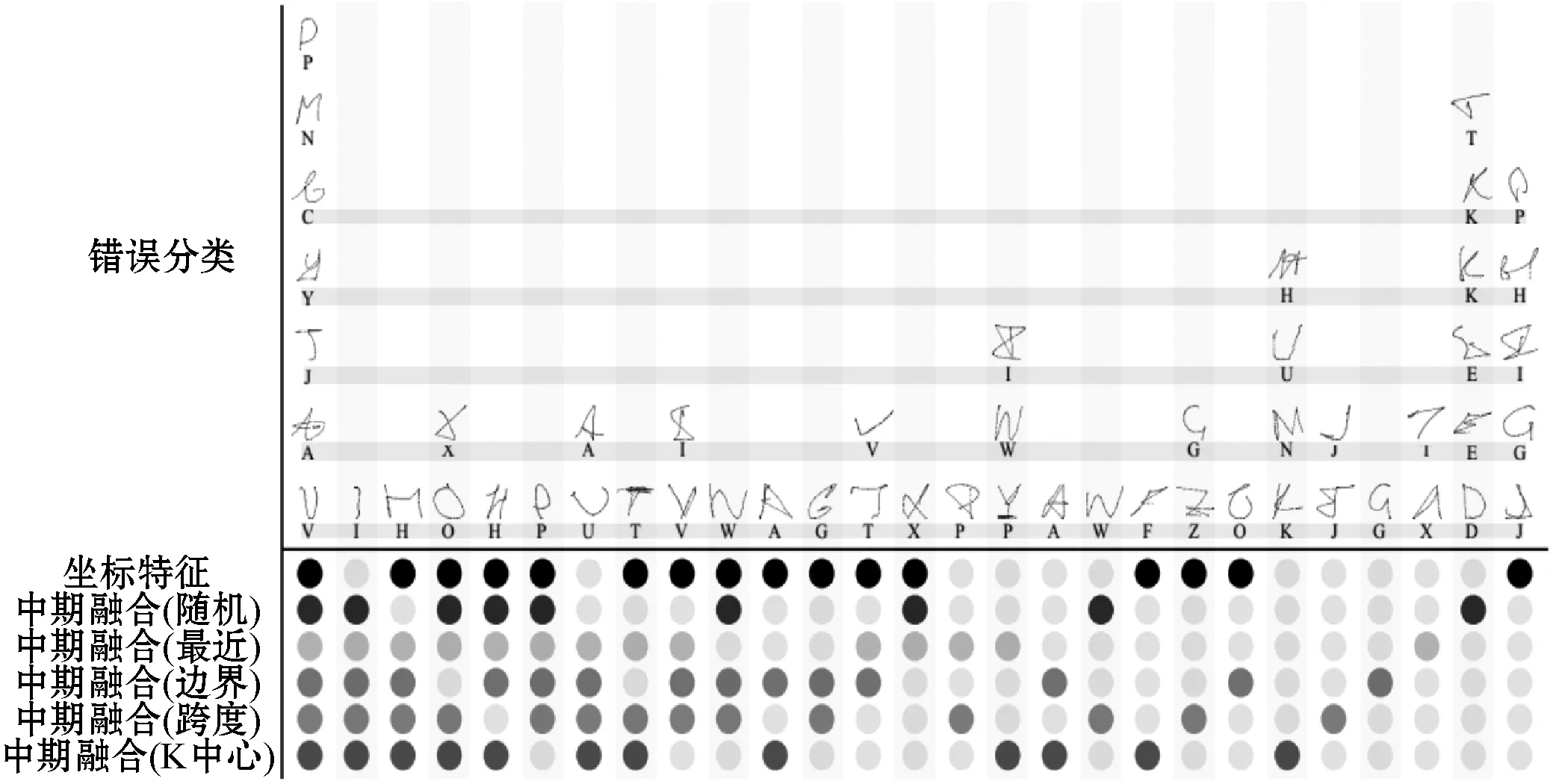
图8 Unipen 1b数据集上的交叉折叠验证
4 结 语
针对动态时间规整时间序列分类中存在的动态匹配信息丢失问题,提出一种基于局部距离特征的多模态融合CNN时间序列分类。通过对几个典型数据集的分类实验结果分析可得出如下结论:(1) 使用中间融合或特征级融合,通常比早期和晚期融合的分类效果更好。(2) 使用高变异原型选择方法往往比相似原型方法在分类效果上更具有优势。(3) 基于局部距离特征的多模态融合CNN时间序列分类能够有效解决动态匹配信息丢失问题,从而极大地提升时间序列分类的精度。
