基于时频对消的跳频信号盲检测算法
2023-05-08赵知劲尚俊娜王李军
王 琳 赵知劲, 尚俊娜 王李军
1(杭州电子科技大学通信工程学院 浙江 杭州 310018) 2(中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室 浙江 嘉兴 314001)
0 引 言
跳频通信具有截获率低、抗干扰能力强和组网方便等特点,是军事通信的主导技术。近年来围绕跳频信号检测、参数估计[1]的研究已成为通信对抗和无线电监测等领域的热点问题。跳频信号检测是通信侦察的主要任务之一。跳频信号为非平稳信号,利用其频率的时变特点可以实现跳频信号检测。文献[2-4]利用信道化接收将跳频信号分解到各个窄带信道中,再在各个信道中检测窄带信号,实现跳频信号检测。文献[2]提出了一种重叠滑动窗方法改进门限,降低虚警概率;文献[3]提出了多层信道化接收,大大降低了计算量;文献[4]利用主分量分析消除突发信号影响,利用短时能量对消去除定频信号影响;但它们都不能检测定频信号。文献[5-7]根据定频和跳频信号频谱的不同特点,采用功率谱对消实现跳频信号检测,但此类方法没有充分利用跳频信号时频谱特点,检测性能有待提高。时频图包含了跳频信号丰富特性,是跳频信号检测与参数估计的重要依据。文献[8]利用多天线接收信号的互相关函数,得到时变功率谱密度矩阵,然后利用功率对消去除定频信号,并从时频图中分割和处理各跳参数,检测跳频信号。文献[9-10]利用跳频信号时频稀疏性,检测跳频信号。但文献[8-10]的方法复杂度都比较高。文献[11-13]利用短时傅里叶变换得到信号时频图,其中文献[11-12]对灰度时频图运用形态学滤波和去均值或边缘检测,消除各种干扰和噪声,当SNR分别大于0 dB和2 dB时,检测概率才达到100%。文献[13]选取时频矩阵局部自适应阈值,对时频矩阵进行截断处理,消除定频干扰,提取跳频信号,但算法的自适应因子确定复杂度高,SNR大于0 dB,检测概率才达到100%。
本文充分利用跳频和定频信号时频谱的不同特点,推导得到跳频信号、定频信号和噪声的时频对消比;采用分数低阶短时傅里叶变换[14]代替短时傅里叶变换,估计得到时频对消比,实现了在脉冲噪声背景下跳频信号盲检测,当信噪比大于-16 dB时对跳频信号检测概率为1。
1 信号模型与算法设计
1.1 信号模型
跳频信号模型可表示为:
(1)

定频信号模型可表示为:
J(t)=a(t)×AJ×ej(2πfJt+φJ)
(2)
式中:AJ、fJ和φJ分别为定频信号的幅度、载波频率和相位。
令仅存在噪声的假设H0,噪声中仅有跳频信号和干扰的假设分别为H1和H2,则用三元假设检验表示接收机截获的观测信号为:
(3)
式中:v(t)为噪声;J(t)为定频信号。
观测信号的短时傅里叶变换可以表示为:

(4)
式中:h(t)为窗函数;STFTs(f,t)、STFTJ(f,t)和STFTv(f,t)分别是s(t)、J(t)和v(t)的短时傅里叶变换。
α稳定分布可以较好地描述脉冲噪声,α稳定分布噪声不存在二阶及以上统计量,因此观测信号需要采用如式(5)所示的分数低阶短时傅里叶变换进行时频分析[14]。

(5)
1.2 算法原理

从时间维度将时频矩阵X(m,n)平均分为两个时频矩阵X1(m,n)和X2(m,n)如下:
(6)
对上述两个时频矩阵做如下运算,分别得到叠加时频矩阵Xadd(m,n)和对消时频矩阵Xsub(m,n)如下:
Xadd(m,n)=[X1(m,n)+X2(m,n)]2
(7)
Xsub(m,n)=[X1(m,n)-X2(m,n)]2
(8)

(9)
(10)
当x(t)是定频信号时,信号的某个频率分量在对应时频矩阵行上的驻留时间长度是整个观测时间T,可以得到E[X1(m,n)]=E[X2(m,n)],可以近似得到:
(11)
E[Xsub(m,n)]=0
(12)
当x(t)是跳频信号时,由于跳频图案由伪随机码控制,实际军事应用中伪随机码的码周期都比较长,因此在观测时间内跳频信号的载频几乎不会重复,所以X1(m,n)、X2(m,n)两个时频矩阵非零值互不重叠,即E[X1(m,n)]·E[X2(m,n)]=0,所以有:
E[Xadd(m,n)]=E[Xsub(m,n)]
(13)
由式(9)-式(13)可见,跳频信号、定频信号和高斯白噪声的Xadd(m,n)和Xsub(m,n)的均值各不相同,因此提出时频对消比检测统计量如下:
(14)
可得跳频信号、定频信号和高斯白噪声的时频对消比为:

(15)
由式(15)可见,利用时频对消比特征参数可以在高斯白噪声背景下同时检测跳频信号和定频信号。

1.3 检测算法
为了适用于高斯噪声和α稳定分布噪声背景下的跳频信号和定频信号检测,利用分数低阶时频矩阵XFLO(m,n)计算时频对消比。根据式(14),时频对消比η的估计如式(16)所示,利用时频对消比η和合适的门限th1和th2可以实现定频信号和跳频信号的检测,检测判决规则如式(17)所示,根据纽曼-皮尔逊准则仿真确定门限th1和th2。当η

图1 时频对消检测算法流程
(16)
(17)
2 算法仿真及性能分析
信号采样频率为fs=10 MHz,采样点数为80 000。采用BPSK调制方式,码元速率为200 kbit/s,跳频图案为[1.25,4.25,0.75,3.75,2.75,3.0,2.0,4.5,0.25,4.5,0.25,3.5,1.0,4.0,0.5,1.75,1.5,3.25],跳速为2 000 hop/s,即跳周期为0.5 ms;定频信号的频率为2.25 MHz。标准α稳定分布噪声的参数为,特征参数0<α≤2,α=2时退化为高斯噪声;对称参数β=0;分散系数γ>0,对应高斯噪声方差;位置参数δ=0。分数低阶短时傅里叶变换使用海明窗,p=0.2。广义信噪比可以表示为:
(18)
式中:A为信号幅度,A=As或A=AJ。
1) 门限确定。窗长P=1 024,滑动长度为P/4=256。本文采用蒙特卡罗仿真确定门限th1和th2。对服从N(0,1)分布的高斯白噪声和γ=1、α为0.5、0.8和1.5的标准α稳定分布噪声各进行10 000次蒙特卡罗仿真,当虚警概率Pf取不同值时,得到th1和th2如表1所示。得到高斯白噪声和γ=1、α为1.5标准α稳定分布噪声的时频对消比η如图2所示。由图可知其均值为3,与理论值一致。

表1 不同虚警概率Pf下的门限th1和th2

(a) 高斯白噪声 (b) α稳定分布噪声图2 高斯白噪声时频对消比
2) 信号时频图。在α=1.5,γ=1的标准α稳定分布噪声背景下,广义信噪比为0 dB时,跳频信号X1(m,n)和X2(m,n)时频图如图3所示,定频信号X1(m,n)和X2(m,n)时频图如图4所示。由图可见,α稳定分布噪声背景下的时频图X1(m,n)和X2(m,n)特性与高斯白噪声背景下一样,且仿真结果与理论分析一致。

(a) 跳频信号X1(m,n)时频图 (b) 跳频信号X2(m,n)时频图图3 跳频信号时频图
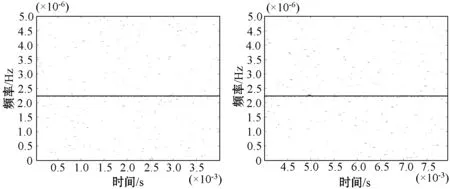
(a) 定频信号X1(m,n)时频图 (b) 定频信号X2(m,n)时频图图4 定频信号时频图
3) 算法性能分析。不同滑动长度对本文算法的影响。窗长P为1 024,滑动长度分别为P/8、P/4和P/2,当虚警概率Pf为10-3时,本文算法的门限th1和th2选取方法同上。在高斯白噪声和α=1.5,γ=1的标准α稳定分布噪声背景及不同广义信噪比下,随机产生定频信号、跳频信号和噪声,1 000次仿真得到本文算法对定频信号和跳频信号的检测概率曲线如图5所示。由图可知,窗滑动长度太大,检测性能下降;窗滑动长度取P/4时性能较好。下文选取滑动长度为P/4。

(a) 高斯白噪声背景 (b) α稳定分布噪声背景图5 不同滑动长度对检测性能的影响
不同窗长对本文算法的影响。窗长P分别为512、1 024和2 048,滑动长度为P/4,当虚警概率Pf为10-3时,本文算法的门限th1和th2选取方法同上。在高斯白噪声和α=1.5、γ=1的标准α稳定分布噪声背景及不同信噪比下,随机产生定频信号、跳频信号和噪声,1 000次仿真得到本文算法对定频信号和跳频信号的检测概率曲线如图6所示。由图可知,窗长增加,检测性能提高。但窗长太长,算法复杂度增大,实时性变差。下文选取窗长度为P为1 024。

(a) 高斯白噪声背景 (b) α稳定分布噪声背景图6 不同窗长对检测性能的影响
由于对比算法[6]在标准α稳定分布噪声背景失效,因此仅比较在高斯白噪声背景下本文算法和对比算法检测性能。当虚警概率为Pf=10-3时,同样用蒙特卡罗仿真得到对比算法门限为th1=1.973 7和th2=2.024 6。在不同广义信噪比下,随机产生定频信号、跳频信号和高斯白噪声,1 000次仿真得到本文算法和对比算法检测定频信号和跳频信号的检测概率曲线如图7所示。由图可见,本文算法检测性能明显优于文献[6]算法,当信噪比为-16 dB时,本文算法对跳频信号的检测概率为1,而对比算法仅为60%,所以大大提高了低信噪比时对跳频信号的检测能力。

图7 与对比算法的检测性能比较
算法的抗噪声功率不确定性分析。设ρ为噪声功率不确定度,当ρ>1.0时噪声方差在(γ/ρ,ρ·γ)内均匀分布;ρ=1.0表示不存在噪声功率不确定性,噪声分散系数是固定值。噪声功率不确定度ρ取1.0和1.1,虚警概率Pf为10-3,在高斯白噪声和α=1.5,γ=1的标准α稳定分布噪声背景及不同广义信噪比下,随机产生定频信号、跳频信号和噪声,1 000次仿真得到的本文算法检测定频信号和跳频信号的检测概率曲线如图8所示。
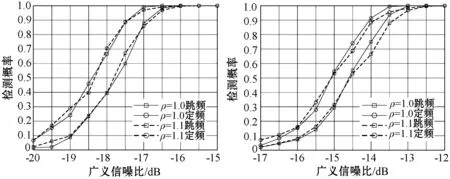
(a) 高斯白噪声背景 (b) α稳定分布噪声背景图8 算法的抗噪声功率不确定性分析
由图8可知,不同噪声背景下,本文算法对跳频信号和定频信号检测都具有较好的抗噪声功率不确定性,当广义信噪比大于-16.5 dB、-13 dB时两种信号的检测概率均达到90%以上。
不同α值时本文算法检测性能分析。α为0.5、0.8、1.5和2.0,当虚警概率Pf为10-3时,在不同广义信噪比下,随机产生定频信号、跳频信号和噪声,1 000次仿真得到本文算法对定频信号和跳频信号的检测概率曲线如图9所示。由图可知,α值越小,α稳定分布噪声脉冲性越强,算法检测性能下降。

(a) 跳频信号 (b) 定频信号图9 不同α值时本文算法检测性能
3 结 语
本文利用跳频信号和定频信号的不同时频特性,设计了一种时频对消比检测统计量,得到一种基于时频对消的跳频信号和定频信号同步检测算法。为了适用于脉冲噪声背景,利用分数低阶短时傅里叶变换计算时频矩阵,蒙特卡罗仿真确定了检测门限。仿真结果表明,该算法可以在高斯噪声和α稳定分布噪声下有效检测跳频信号和定频信号,提高了现有基于时频分析的检测算法在低信噪比下检测性能。
