计及实时碳减排的产消群价格型需求响应机制
2023-05-08朱月尧吴星辰华昊辰
朱月尧, 祁 佟, 吴星辰, 刘 迪, 华昊辰
(1. 国网江苏省电力有限公司 淮安供电分公司,江苏 淮安 210000; 2. 山东科技大学 智能装备学院,山东 泰安 271019; 3. 清华大学 自动化系,北京 100084; 4. 河海大学 能源与电气学院,南京 211100)
2021年9月,《中共中央 国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》(中发[2021]36号,以下简称为36号文件)强调了能源绿色低碳发展在“碳达峰”“碳中和”目标上的关键作用[1].36号文件的出台意味着电力体制改革不仅是电力行业的内部要求,更是“双碳”目标背景下社会经济发展的必要举措.电价改革是电力体制改革的核心内容,考虑碳排放以完善电价机制是减少电力行业碳排放的有效途径.
以电力市场和碳市场为手段的市场机制是电力行业低碳发展的保障.受到碳排放政策的制约,当化石能源发电企业的实际碳排放量高于配额量时,企业为了足额履约,需向富裕配额量的企业购买一部分配额,否则将面临惩罚.在碳市场中,碳排放量过大的化石能源发电企业的成本(以下简称为碳成本)将会增加[2],碳配额富裕的部分发电企业则可通过售卖配额的方式获得额外的收益.这种成本的增减可以促进企业自发减排.在碳排放成本的影响下,市场中电力供给与电力需求的动态平衡会受到碳交易的影响[3],进而供需两侧的优化决策也随之变化.
由于可再生能源的调节灵活性较差,所以在高比例新能源的新型电力系统内,需求侧管理在电力系统的高效运行中愈发重要[4-5].电力市场准入机制的约束使得大量中小型用户不能够直接参与电力市场,需要通过售电商从市场中获得所需电量[6].为了实施更加高效、经济的需求响应计划,文献[7]提出构建边云协同框架实现住宅需求响应的预测.文献[8]综合分布式负荷的需求响应提出基于云边缘计算架构的能量管理算法.文献[9]提出基于云边协同的需求响应调度策略用于优化调度的时延问题.为了提升自身效益,售电商可以面向用户实施需求响应以引导用户改变电力消费行为.需求响应可以分为价格型和激励型,其中激励型需求响应更为灵活,而价格型需求响应包括尖峰电价、分时电价和实时电价等[10-11],更加适合大范围推广.目前分时电价机制已经在我国全面普及,因此本文关注价格型需求响应机制.文献[12]基于分时电价构建售电决策模型来引导用户用电.文献[13]将分时电价的优化问题转化为博弈问题,对用户的功率求解到最优.文献[14]根据实时电价设计微网运行模式,优化微网内功率分配.文献[15]考虑到电力市场电价的随机性,针对随机电价利用模型预测确定最优电力调度方案.文献[16]提出基于折扣因子的需求响应机制,考虑用户间的差异性.但上述研究均未考虑需求侧的碳减排问题.
针对能源系统中的碳排放问题,目前已有一些研究成果.文献[17]对电力碳排放权交易市场进行扩展研究.文献[18]从发电、输电、配电等环节考虑电力行业中碳排放的变化.文献[19]分析欧盟碳市场与电力市场之间的相互作用机理.文献[20]从社会效益达到最优角度出发,提出电碳联动前提下的发电权交易模型,但所提出的模型难以从数值上准确反映出电、碳二者的耦合关系.上述研究多是从发电侧的角度针对能源系统的碳排放展开研究,但供给侧的发电量会随着电力消费需求变化,因此能源系统碳排放实际上是由消费者引起的,能源系统的碳排放成本最终也应由需求侧承担[21].
目前电力消费的碳排放多基于联合国政府间气候变化专门委员会的计量方法,采用固定系数计算单位电力消费的碳排放.由于可再生能源出力占比不同,电力系统中不同时段单位发电量产生的碳排是变化的,目前基于固定系数的需求侧电力消费碳排放计量方法很难反映不同时段电力消费引起碳排放的差别,所以无法引导用户改变电力消费行为实现碳减排.
综上,为了充分挖掘需求侧可调节资源的灵活性潜力,引导用户改变电力消费行为实现碳减排,需解决两个关键问题:一是如何将碳排放量和发电量之间的耦合关系融合到电价机制中;二是如何在电价机制加入碳成本的情况下,将固定碳成本转化为灵活碳成本.针对以上问题,本文在建立碳排放量与光伏发电量数值关系的前提下,将折扣因子(γ)的概念引入价格型需求响应以及碳排放调节当中,使产消者[22]通过积极响应需求响应机制在不同时段获得更低的折扣价格.利用这种方法,在引导用户积极响应改变用电行为、加强分布式能源就地消纳的同时,还能达到更好的碳减排效果.
1 实施架构及碳减排分析
目前越来越多用户群体装设分布式光伏,本文将这些用户群体定义为产消者[22].假设每个用户均装设有智能终端,可以对用户内部的负荷优化控制[23].售电商作为整个运营系统的核心[24],当产消者的光伏发电量有剩余时,会对其进行回收,并将多余的电量出售给外电网,以此来达到供需平衡.传统电力行业的能源消耗主要来源于高污染煤炭.由化石能源发电作为主力电源的供应侧,是电力行业碳排放的主要来源.而可再生能源发电过程中的碳排放可忽略不计,因此利用可再生能源代替化石能源,可有效实现发电侧的清洁化.针对我国以火电为主的现状,假设从市场中购电需承担碳排放责任,而本地分布式光伏所发电量的碳排放为0.为了引导能源系统碳减排,碳排放引起的环境污染成本需要发电企业承担,并通过碳配额和碳交易市场实现,本文称之为碳排放成本内部化.不同于以往的碳配额分配[25]调节,本文将传统发电后形成的碳排放量内部化后的碳成本直接归算到电价中进行传导.售电商的运营架构简图如图1所示.
由图可见,将火力发电产生的碳排放内部化为碳成本,外电网将由碳成本和基础电价共同构成的购电和售电价格发送给售电商.其中,市场的供求会决定电力市场下的电力价格,而其他环境下的电力价格将由政府政策决定.此外,在电价制定过程中,售电商除了与外电网进行信息与能量交互以外,与周围其他售电商之间也可以进行交互.某个区域内的多个售电商之间可以相互传递购、售电量以及购电、售电价格信息,合作协商统一制定电价后向外电网进行购电,由此可达到降低批发成本的目的.对发电商和售电商的相互作用进行分析,将碳成本归算到外部电价中,售电商在确定价格信号时,统一考虑电力需求侧贡献以及碳减排的贡献.售电商根据所获取的外部电网价格信息来设置产消者的价格信息,而后将价格信息传送到智能终端.智能终端接收信息后对产消者进行用电调节,并将调节后的信号重新发送到售电商.这个过程中产消者本身不会产生碳排放,碳成本被引入价格中进行传导,以形成减少碳排放条件下的价格型需求响应机制.
不同类型负荷的产消者具有差异化的调节弹性[26].为体现用户的差异,文献[27-28]根据用户参与需求响应的贡献给予不同激励.在价格型需求响应中,每个用户的单位电价相同,为体现用户贡献的差异,提出基于折扣因子的价格型需求响应激励机制.参考博弈论中Shapley值的计算方法,用户在调节中对经济成本降低和碳减排的贡献越大,获得的折扣就越大,从而用电成本越低.产消者无论具有何种调节弹性,均能经智能终端决策后在同一时段内得到相同的购电、售电价格以及折扣系数,以此来保证机制形式上的公平性.除此以外,整个系统的最终结果均应呈现积极趋势,即当系统中的用户终端参与调节的积极性越高,对系统调节贡献越大时,其所能得到的折扣也越大,以此保证结果的公平性.
不同于传统的价格型需求响应,售电商除了需要决策产消者单位购电价格Pbuy外,还需要决策相对应的折扣因子,即最终产消者要结算的电价为γPbuy,且γ=γ1(k,ΔN)γ2(k,ΔL),γ1为碳成本折扣因子,γ2为电价折扣因子,k为折扣因子中的折扣系数,决定折扣力度的大小,ΔN为产消者碳减排程度,ΔL为产消者的负荷改变量,γ1(k,ΔN)与产消者碳减排程度存在一定关系,产消者碳减排程度越高,碳排放成本越低,从而承担的碳成本价格越低;γ2(k,ΔL)与产消者的负荷改变存在一定关系,当产消者负荷的改变量往正方向变大时,折扣因子减小,所需结算的基础电价越低,从而实现电力需求侧响应与碳减排的共同激励作用.
2 模型构建
2.1 碳排放模型
以光伏发电为例,将某系统产消者所需的基础电量看作由产消者光伏发电和外来发电组成的一个整体.即当光伏发电量增加时,可相应减少外来发电量,使得碳排量减少.每日系统需要的总电量定义为Q,每日外来发电量定义为M,从需求侧出发产消者每日所需光伏发电量定义为E,则Q=M+E.将年碳排放约束折合为每日碳排放约束N,求得满足每日碳排放约束时外来发电量M的约束条件为M≤N/g,其中g为二氧化碳排放因子[29],表示每度电所产生的二氧化碳排放量,具体取值以算例所选取的区域为准.产消者每日所需光伏发电量为E=1-M/Q.同时,产消者每日实际光伏发电量e与每日所需光伏发电量E满足e≥E.将每日实际光伏发电量多于每日所需光伏发电量的部分定义为碳减排程度,则其公式为ΔN=e-(1-M/Q).综合上述得:
ΔN=e+N/gQ-1
(1)
由式(1)可得,若结果为正,则表示每日实际光伏发电量超出每日所需光伏发电量,所需外来发电量小于满足约束条件时的外来发电量,此时碳减排程度增大;若结果为负,则每日实际的光伏发电未达到每日所需光伏发电量,碳减排程度减小.同时,将每日实际光伏发电量与每日碳排放量(n)建立关系[30],表示为n=(Q-e)g.
为了使用户的结算电价在一个合理的范围,折扣因子在满足碳成本灵活性的同时,应始终保持在某一范围内.因此引入一个虚拟函数F(x),能够将其映射到一个连续单调的有界范围内.基于此将产消者i的碳成本折扣因子γ1的表达式[31]设计为γi1=1-F(kΔNi),其中ΔNi为产消者i的碳减排程度.由于双曲正切函数存在有界性,取值范围始终保持在[-1, 1],能满足折扣因子保持在某一范围内的特点;且其单调性能够保证在自变量正向或负向增长这两种情况下折扣因子不会存在效果相同的情况.因此,在双曲正切函数的基础上设计碳成本折扣因子.需要指出的是,任何满足连续单调的有界函数都可作为虚拟函数.以双曲正切函数为例,则碳成本折扣因子γ1的表达式为
γi1=1-F(kΔNi)=1-tanh(kΔNi)
(2)
(3)
当产消者的碳减排程度正向增大时,折扣因子随之减小,此时产消者所承担的碳成本减少;当碳减排程度减小,甚至为负减排时,折扣因子增大,产消者不仅需要承担已存在的碳成本,还需承担由折扣因子增加带来的额外碳成本.基于此,本文碳成本折扣因子可使得产消者对碳排放进行控制,从而达到减排效果.同时,由式(3)可知,无论k如何取值,折扣因子始终能稳定到0~2.
2.2 售电商模型
售电商的最终目的是实现收入最大化.外部电网和产消者均可对售电商的收益产生影响,售电商可采取制定折扣因子来引导改变产消者的用电行为,使得自身收益得到优化.定义售电商收益为I,其收益模型设置如下:
PinLin+PoutLout
(4)
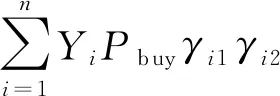
产消者功率约束应满足如下要求:
(5)
同时,传输功率约束为Lin≤Pmax,其中Pmax为售电商最大的传输功率.电价折扣因子γ2与碳成本折扣因子模型类似,同样以双曲正切函数为例,表示如下:
γi2=1-tanh(ksgn(∑Vi-∑Bi)Di)
(6)
式中:Vi为第i个产消者的光伏发电量;sgn为符号函数[32],当光伏发电量大于基线负荷时取值为1,表示负荷向正方向调整,当光伏发电量小于基线负荷时取值为-1,表示负荷向正方向调整;Bi为第i个产消者的总基线负荷;Di为第i个产消者的负荷调节量,其值为Di=Ai-Bi,其中Ai为第i个产消者的实际用电量.
理想情况下,希望总体折扣因子具备以下几个特点:
(1) 折扣因子可以体现碳减排程度和负荷调节量两个方面对折扣力度调整的贡献,且具有公平性,即用户最终享有折扣仅与其贡献值有关,总体上折扣因子应做到引导用户向降低负荷的不平衡、向增大碳减排程度方向调整.
(2) 折扣因子应保证无论碳减排程度或负荷调节量如何,均能使折扣因子在某个范围内,避免出现由于折扣或成本过多而产生价位不合理的问题.
由此,总折扣因子为
γi=γi1(k,ΔNi)γi2(k,ΔLi)
(7)
由式(7)得折扣因子和产消者负荷调节量、碳减排程度的关系如图2所示.由图2可得,综合考虑碳减排程度、负荷调节量两个因素,当产消者的碳减排程度正向增大、负荷调节量增加时,折扣因子随之减小,此时产消者需承担的电价减少;当负荷调节量减少、碳减排程度减小,甚至为负减排时,折扣因子增大,产消者不仅需要承担原有电价,还需承担由额外碳成本和额外电价所增加的费用.基于此,所提出的折扣因子在碳排放进行控制的同时,也可起到平衡负荷调节量的作用.当折扣系数k取不同值时,折扣因子的变化灵敏度随折扣系数的增大而增大;同时,折扣因子始终能稳定到0~4.
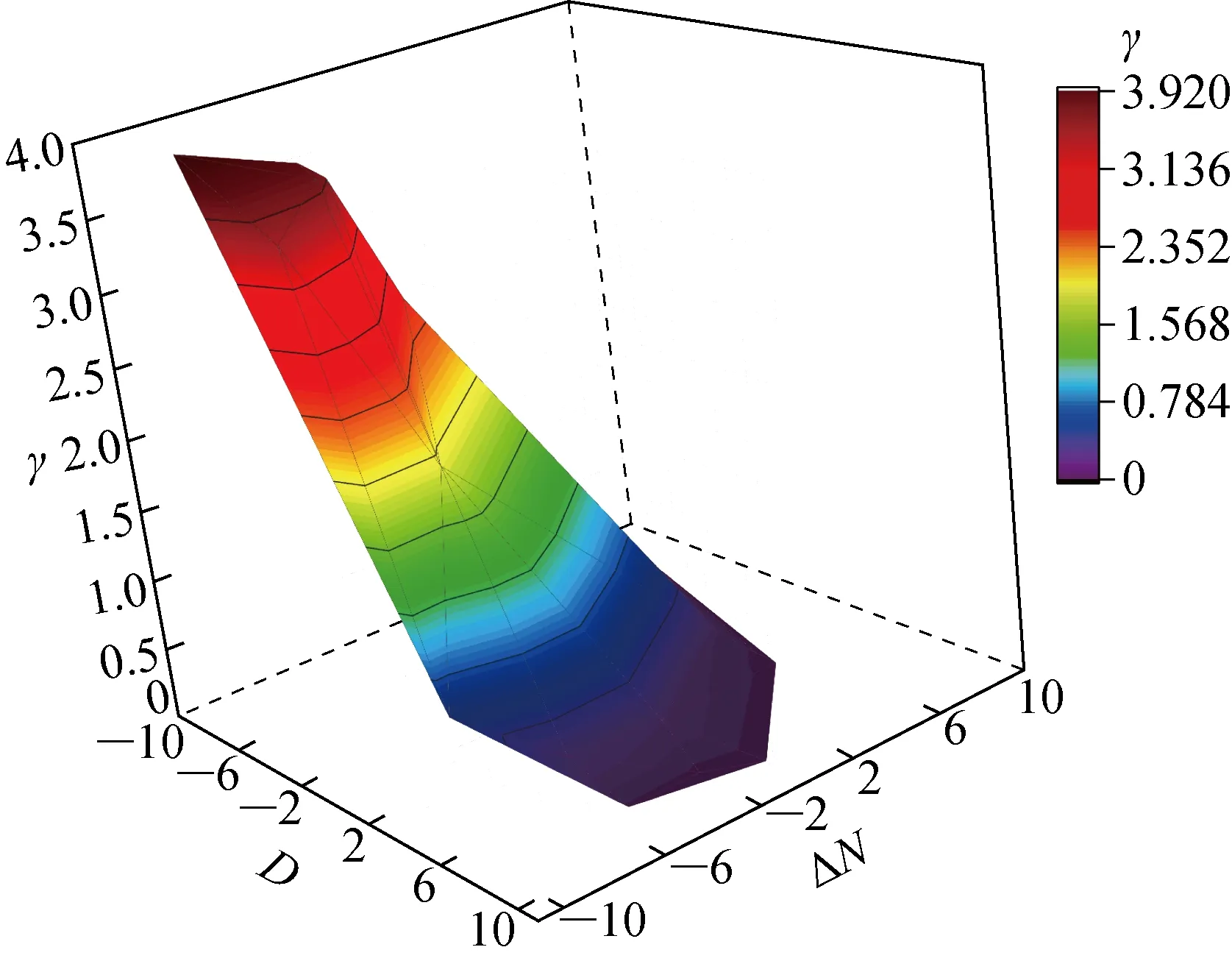
图2 折扣因子随碳减排程度和负荷调节量变化
2.3 产消者模型
产消者自身用电也会产生收益,此收益与产消者的用电量呈正相关.定义产消者收益为U,第i个产消者收益可表示为如下的分段函数[33]:
Ui(Ai,ωi)=
(8)
式中:ωi为第i个产消者的弹性系数;υi为第i个产消者的设定参数.
产消者除了获得部分效益,还需支付一些成本.所要支付的成本由两部分组成,一部分是产消者在向售电商购电时需支付的成本,另一部分是产消者随实时电价调整自身的用电行为所造成的舒适度损失.其中购电经济成本又可分为两部分,一部分是基础购电成本,另一部分是额外碳成本.
当产消者的使用电量偏离基线负荷时,会导致舒适度损失,定义舒适度损失[31]为
(9)
式中:βi、αi为舒适度损失函数的设定参数;|Di|为第i个产消者的负荷调节量的绝对值.
综上,定义产消者效益为
Oi=Ui-Ci-YiPbuyγi+SiPsell
(10)
式中:YiPbuyγi为第i个产消者向售电商购电后损失的总收益;SiPsell为第i个产消者将光伏发电量卖给售电商后获得的收益.

3 边云协同模式下的迭代优化策略
在低碳条件约束下,售电商为得到最优电价及折扣系数从而达到效益最优,需要在考虑碳成本的情况下,了解每个时间段的产消者在不同需求响应激励时的响应情况.边云协同计算架构能够有效提高计算速度和计算灵活性[34].在主从博弈模型框架下,基于边云协同架构,将售电商作为云端,利用折扣系数改变价格引导用户的用电行为,以促进可再生能源的就地消纳以及碳减排行为.将智能终端经过优化从而决策出最优结果视作一个“应用实例”.为了解决电价及折扣系数组合过多造成的不经济性,本文通过优化实现售电商与产消者智能终端的互动协同,决策得出每个时间段的最优电价和折扣系数.
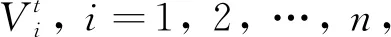
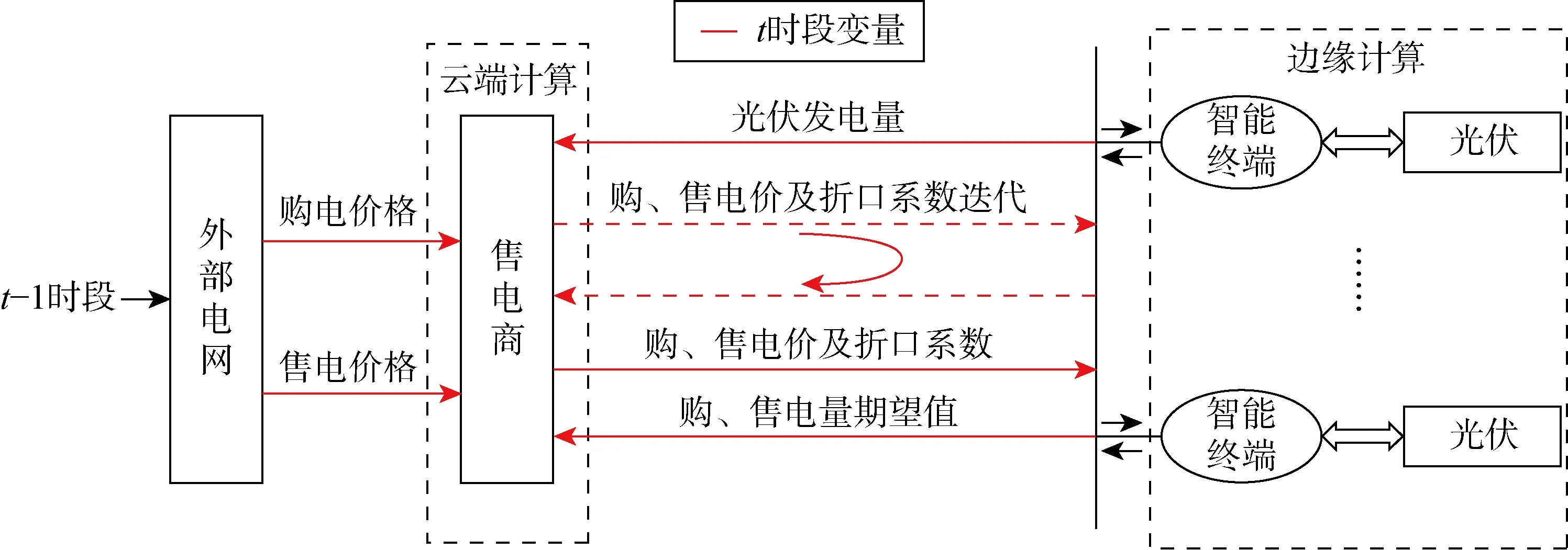
图3 边云协同优化时序图
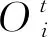
此次优化都是对多变量求解最优值的问题,并且求解过程中,售电商和产消者求解的最优值之间存在耦合,二者相互影响.求解过程中,希望所选取的算法能够高效准确,保持多样性的同时提高收敛性,因此选取粒子群算法(PSO)进行求解[35].
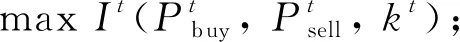
(11)
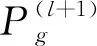
(12)
经由智能终端决策后的值才可以计算出It的值,故优化时需要进行多次迭代.
智能终端在运行过程中,需要判断在满足传输功率约束的前提下是否保证经外电网和产消者购入的电量与售出电量的实时平衡.若不满足条件,为避免不能满足功率约束条件的值成为最优值,适应度将被设置成负无穷.
求得每次经迭代后的个体和粒子种群最优位置后,需要更新各个粒子的速度和位置,更新公式[36]如下:
(13)
(14)
式中:c1、c2为加速常数,一般取值范围为0~4;ρ为约束因子,其作用是控制速度Vi的权重;r1、r2为区间[0, 1]的随机数.
以粒子群算法为基础的边云协同模式下的迭代优化策略流程如图4所示,详细运算过程如下:
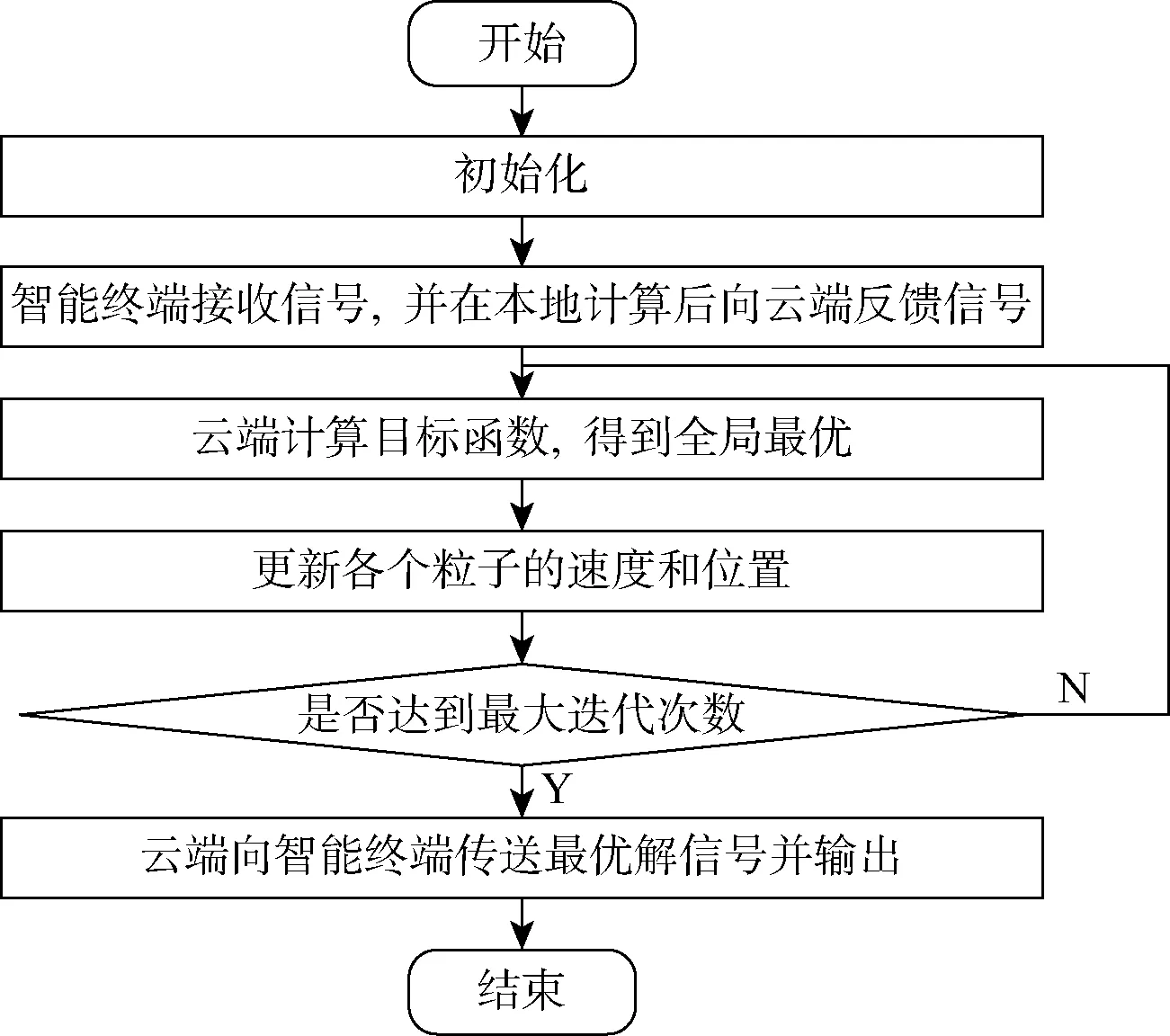
图4 以粒子群算法为基础的边云协同模式下的迭代优化策略
(1) 随机初始化每个粒子,设置粒子群大小,以及售出电价、购买电价和折扣系数的初始值.
(2) 产消者智能终端收到价格信号并进行优化,同时在本地计算购买电量、售出电量的期望值后将信息反馈到云端售电商.
(3) 云端售电商根据反馈信息计算各个粒子的目标函数,找到各粒子当前个体极值以及整个粒子群的全局最优解.
(4) 利用式(13)和式(14)更新各个粒子的速度和位置.
(5) 判断是否达到最大迭代次数,若达到,则将最优解信息传送到智能终端,算法结束;若未达到,重复步骤(3).
4 仿真分析
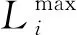
为了检验添加碳成本折扣因子机制在产消者光伏发电量满足或不满足自身需要前提下引导用户积极参与决策的激励有效性,同时,为了达到检验碳成本参与系统运营的机制作用效果是否优于无碳成本参与系统运营的机制作用效果的目的,设计两种不同的情况,分别为产消者光伏发电量大于需求量和产消者光伏发电量无法满足需求量.二者本质区别是产消者基础光伏发电量的多少.情况1中,设置光伏发电量取值范围为[0, 2],基线负荷为[4, 10],售电商从外电网购进电价为1,售电价格为0.6;情况2中,设置光伏发电量取值范围为[6, 10],基线负荷为[2, 4],售电商从外电网购进电价为0.5,售电价格为1.2.其中,当模拟过程为情况1时,产消者的光伏发电量远小于其负荷;当模拟过程为情况2时,产消者的光伏发电量大于其负荷.
为进一步验证本文算法的稳定性,进行多次仿真,定义迭代次数为n,适应度为F,每次迭代结果如图5所示.由图可见,同样参数下的多次仿真结果收敛于某一值附近,最优适应度处于132上下,最大适应度和最小适应度的结果存在较小的误差,且小于2%,证明算法具有较好的稳定性.同时,考虑到粒子群算法中的通信延迟问题,在算法程序中增加一项时延函数用于模拟仿真过程中的通信延迟,文献[37]将每次迭代通信延时设置为0.25 s,本文保守设计为0.7 s.经模拟后算法总计算时间为557 s,迭代的延时时间对求解速度影响可忽略.
图5 粒子群算法迭代结果图
在光伏发电量分别大于和小于需求量的情况下,产消者及售电商的收益如图6和图7所示.由图能够分析出,本文粒子群算法在迭代60次后两种情境下产消者和售电商的效益曲线基本达到平稳,在经过100次迭代之后,产消者和售电商效益曲线得到最终稳定.其中在光伏发电量大于需求量的情况下,从效益曲线中可得:产消者的综合效益最终达到 2 259.26 元,售电商的综合效益达到131.50元.在光伏发电量无法满足需求量的情况下,产消者的收益为 2 452.93 元,售电商效益为113.60元.
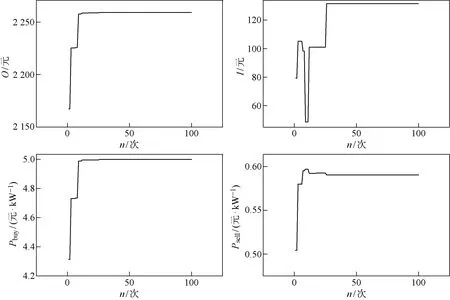
图6 情况1下产消者用户及售电商效益
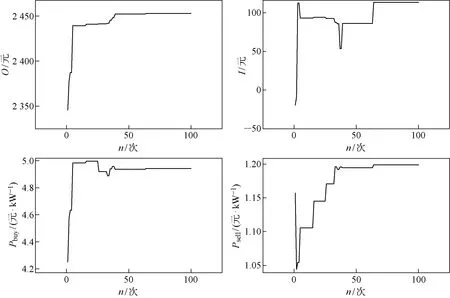
图7 情况2下产消者用户及售电商效益
结合两种不同情况下所得出的优化价格可以分析出,当处于情况1时,产消者优化得出的光伏售出价格较低,购买价格较高,以此可以引导产消者降低购电需求,从而促进碳减排;当处于情况2时,售电商优化得出的光伏回收价格相较于电量不足的情况较高,以此可以引导产消者调节负荷的使用情况.同时,因光伏过剩,无需购进电量,售电商也可减少从外电网购买电量,也可以促进碳减排.在这两种情况下,从购电价格曲线可以看出,若产消者不积极参与调节决策,那么产消者的用电成本会较高.但当结合本文所提的机制后,产消者可以通过调节负荷获得不同的电价折扣.在两种情况下将是否考虑碳成本进行对比,将产消者用户定义为US,在碳成本灵活化后对不同积极性参与决策调节的产消者可以获得的电价折扣结果作图,如图8和图9所示.
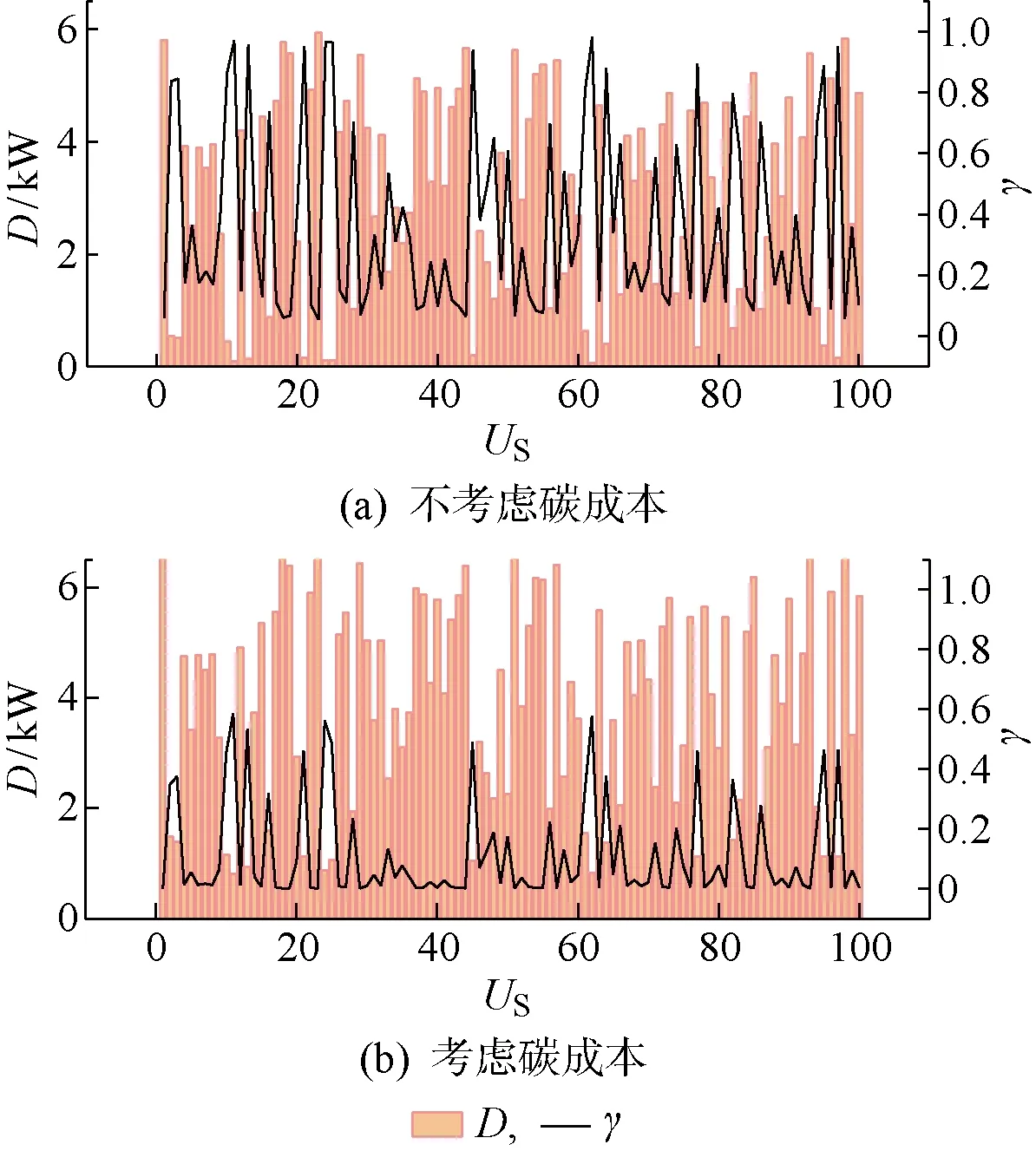
图8 情况1下产消者的负荷改变量及结算折扣
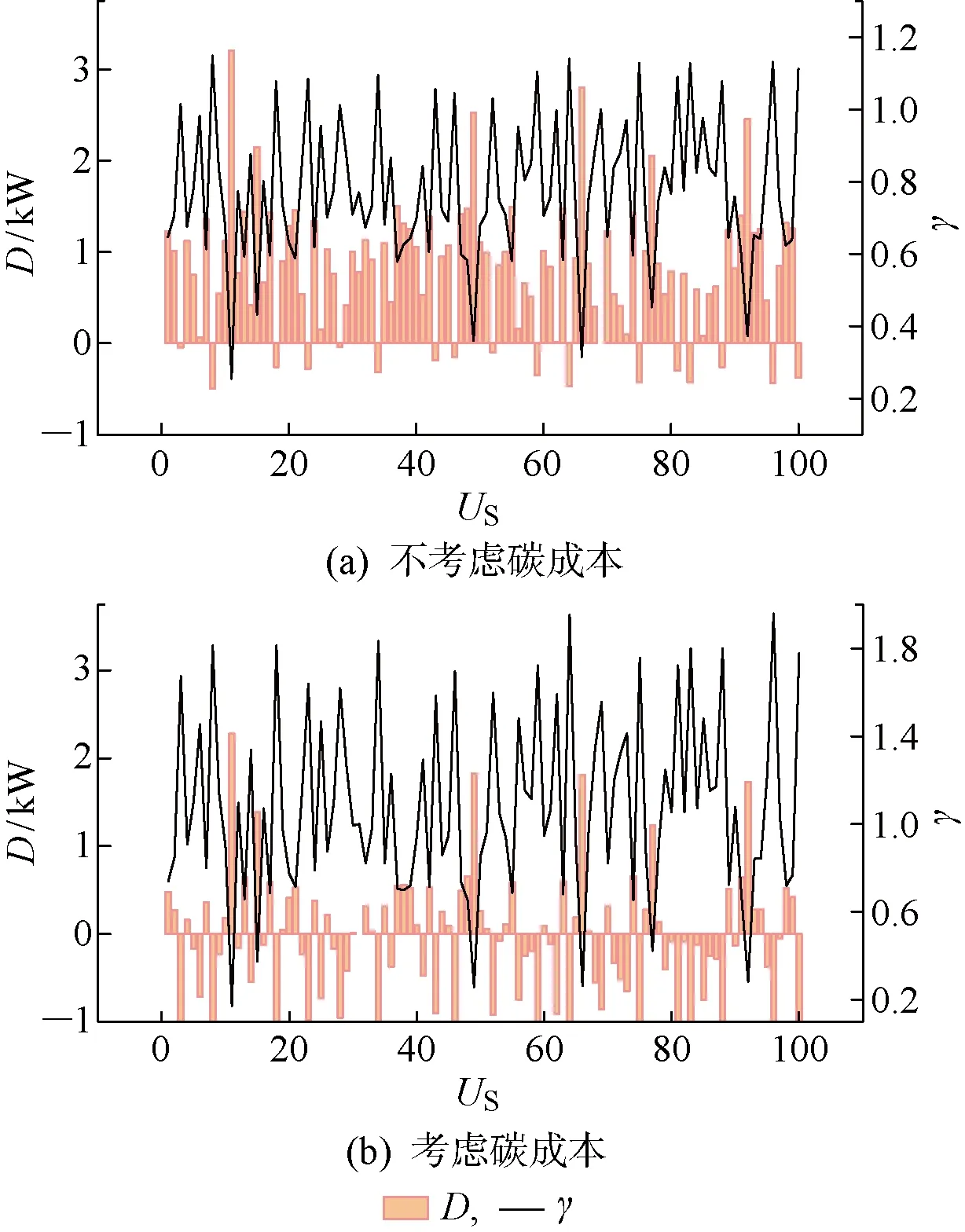
图9 情况2下产消者的负荷改变量及结算折扣
由图可见,在光伏发电量大于需求量中,不考虑碳成本情况下,积极参与响应的产消者能够以小于0.1的折扣进行购电;考虑碳成本情况下,积极参与响应的产消者能以低于0.02的折扣进行购电.因此在考虑碳成本情况下,产消者能够获得更低购电折扣.随机以第98个产消者为例,其在不考虑碳成本情景下能够以0.87作为折扣进行购电,其原始负荷是9.41 kW,经机制调节后原始用电负荷变为3.54 kW.在考虑碳成本情况下, 其能够以为0.018作为折扣进行购电,其基线负荷为9.41 kW,经机制调节后原始用电负荷变为2.89 kW.因此,考虑碳成本情况下比不考虑碳成本情况下的负荷调整幅度更大,更能引导产消者的负荷调节.
由图9可见,在光伏发电量无法满足需求量时,考虑与不考虑碳成本均出现折扣值大于1的情况,此时产消者所需承担的电价会高于原来的基础电价,产消者的经济成本增多,产消者负荷调节会往反方向进行,减少用电量,通过这种调节使购电成本上升带来的损失有所减小.综上,在两种情况下,对比考虑碳成本比不考虑碳成本两种条件,可以看出考虑碳成本时产消者的负荷调整量幅度更大,降低产消者用电量也更为明显.
同时,从图8和图9中可以看出,考虑碳成本的机制对产消者负荷平衡所做出的贡献会更多于不考虑碳成本时的机制.考虑碳成本时产消者可以用更低折扣进行购电,负荷调整幅度也更大;反之,不考虑碳成本则需要支付更高的购电成本,负荷调整幅度也更小,更能突出在考虑碳成本时的优越性.
为了进一步探究本文考虑碳成本机制的优越性,将在不考虑碳成本算法和机制下产消者、售电商的效益以及购电量和售电量与所提算法和机制下相应方面进行比较.在光伏发电量大于需求量和光伏发电量无法满足需求量这两种情况下不同机制的产消者、售电商的收益以及购电量和售电量如图10和图11所示.
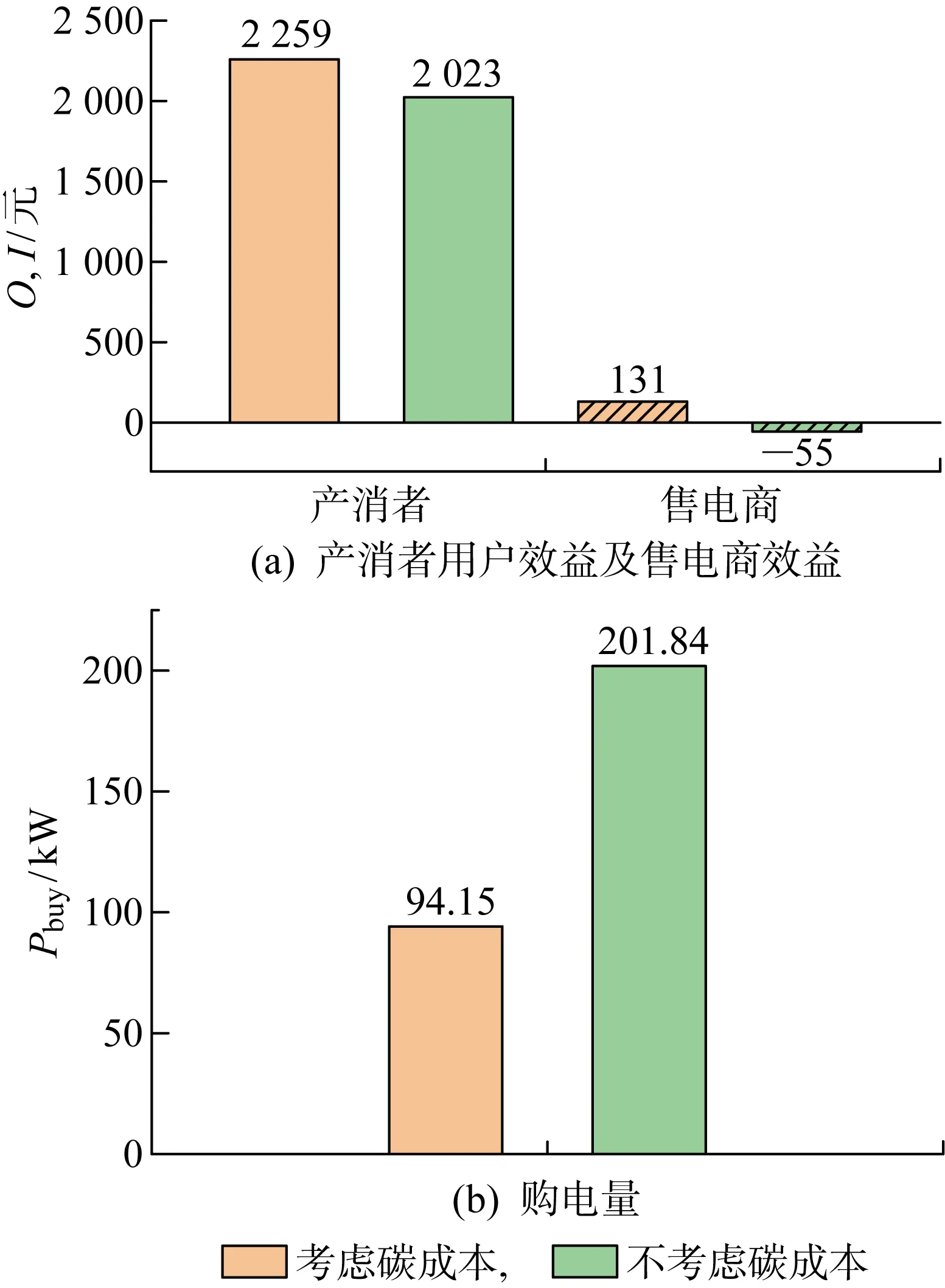
图10 情况1优化结果对比
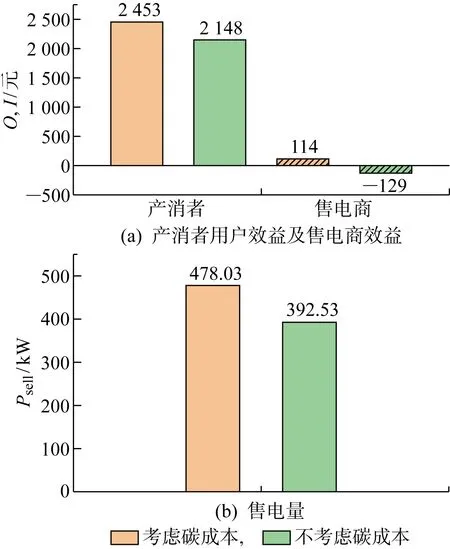
图11 情况2优化结果对比
从图10和图11中能够看出,在光伏发电量大于需求量与光伏发电量无法满足需求量情况下,无论是否考虑碳成本均能使得产消者用户获得较高的收益,并且考虑碳成本时的机制能够更有效地提升售电商的收益,在光伏发电量大于需求量中售电商的收益达到了131元,比不考虑碳成本算法和机制下的优化结果提高2.4倍.考虑碳成本的算法和机制下的购电量明显低于不考虑碳成本下的购电量,将此信息反馈到售电商处,售电商也可减少从外电网的购买电量,从而起到减少外电网电量的作用,以此增大碳减排力度,更大地提高碳减排程度.
在光伏发电量无法满足需求量时,考虑碳成本的售电量明显高于不考虑碳成本的售电量,且售电商收益在不考虑碳成本情况下可以提高0.9倍,侧面反映出售电商从外电网的购电量在考虑碳成本情况下可以更低,仍然能够起到减少外电网电量的作用,碳减排程度提高;同时,考虑碳成本时产消者以及售电商的效益较不考虑碳成本时有大幅度提升.
5 结论
针对提升碳减排力度和实现产消群功率平衡问题,从售电商的角度出发,提出考虑添加折扣因子情况下的电价机制.售电商统一设定相同的基础购买电价和售卖电价后将信号传送到所有产消者.为了达到挖掘产消者不同调节弹性的同时,将固定碳成本转化为灵活碳成本,通过价格调节降低碳排放的目的,引入折扣因子这一概念,加强系统中产消者光伏发电与碳排放的耦合,使得积极响应调节的产消者能够用更低的折扣购电,同时在电价信号的返回过程中对碳排放进行调节,以达到调节负荷的同时减少碳排放的效果.进而提出基于边云协同模式的价格型需求响应电价策略,以售电商的收益最大化作为目标,优化不同时段的价格和折扣.
从仿真实验结果能够看出,在产消者发电量少于和多于需求量两种情况下,考虑碳成本折扣因子的机制均能使售电商和产消者收益提升.而且在两种不同情况下,考虑碳成本时能够有效引导用户降低负荷高峰、填补负荷低谷,实现发用电平衡,并减少整个运行系统的碳排放.同时,在仿真过程中发现,折扣系数最优取值介于0.3~0.6,过小会导致负荷调节量较大时才能体现出折扣因子作用,而过大导致折扣对负荷调节的反应过于灵敏.
在未来的研究工作中,将进一步考虑激励型需求响应.采用实时弹性奖励策略,更有效地激励用户改变用电行为.在此基础上需要对本文提出的折扣进一步优化,解决取值问题.本文仅考虑售电商与产消者之间的交易,而产消者间的相互交易可能会进一步提升系统运行效率,因此未来将进一步探索考虑用户间交易的合作或非合作博弈问题.此外,多售电商共存环境下如何解决售电商与用户间的多对多博弈问题,达到系统最优运行状态,也将进一步探索.
