直升机着舰起落架动态响应

刘湘一，宋山松，吴 靖，康之卉

（1.海军航空大学，山东 烟台 264001；2.91967部队，河北邢台 054000）

舰载直升机着舰时，着舰区域十分狭小，且因受到舰船上部建筑的影响，平台上方明显的气流变化会使直升机的姿态保持难度加大[1-2]，从而具有了更大的下沉速度。同时，由于舰船在海面的运动是六自由度的运动，因此，直升机通常是单轮着舰，这使得起落架载荷加大。对直升机着舰时起落架的动态响应进行研究，分析不同情况下着舰动态响应的变化规律，对直升机安全着舰具有理论指导意义。

文献[3]对轻型直升机起落架的载荷进行了分析；文献[4]对某型直升机主起落架小升力系数下的着陆性能进行了分析；文献[5]对某型直升机主起落架落震实验载荷异常进行了分析；文献[6]对直升机起落架着陆载荷及参数影响进行了分析；文献[7]基于LMS Virtual.Lab 对直升机起落架着陆载荷进行了分析；文献[8]基于LMS Virtual.Lab 对直升机着舰动力学仿真分析；文献[9]基于ADAMS对直升机着舰动力学特性进行了仿真；文献[10]建立了直升机舰面动力学模型，主要对受计及舰面共振影响的起落架缓冲器性能进行分析；文献[11]通过建立直升机着舰动力学模型，进行了舰碰撞研究；文献[12]对直升机着舰起落装置进行了动力学仿真建模研究；文献[13]提出了1 种基于PCA-BP 的直升机起落架着舰载荷评估方法，以此来评估直升机起落架在飞行包线边界及包线扩展状态下的着舰载荷。上述研究对所建模型都进行了相应地简化，且对直升机着舰动态响应的影响因素分析都不够全面。

本文通过建立直升机机体/起落架/舰船耦合着舰动力学模型，将着舰过程中直升机着舰姿态和舰船的姿态联系起来，计算出起落架的动态响应，分析着舰时直升机的质量、接舰姿态、下降速度等因素对直升机起落架载荷的影响。

1 建立坐标系

文中采用的主要坐标系如图1所示。

图1 坐标系Fig.1 Coordinate systems

1）惯性坐标系oI-xIyIzI：原点oI位于海平面上，与地球相对静止；oIxI轴与舰船速度方向重合，指向后方；oIzI轴垂直向上；oIyI轴指向右舷。

2）舰船坐标系oS-xSySzS：原点oS位于舰船的转动中心；oSxS轴与舰船纵向轴线一致，指向后方；oSzS轴垂直于舰船基准面，指向上方；oSyS轴指向右舷。相对惯性坐标系具有横摇角φS、纵摇角θS。

3）舰面坐标系oP-xPyPzP：与舰船坐标系平行并保持相对静止，原点oP位于直升机舰面起降平台中心线。

4）机身坐标系oF-xFyFzF：oF点在机体的转动中心；oFxF轴为机体滚转轴，沿机身纵向轴线，方向指向后方；oFyF轴为机体俯仰轴，在机身水平面内，方向指向左方；oFzF轴为机身偏航轴，垂直于机身水平面，方向指向上方。

2 直升机机体/起落架/舰船耦合模型

2.1 起落架的布置

以常见的前三点式起落架为例，起落架在机身坐标系中的布置，如图2所示。

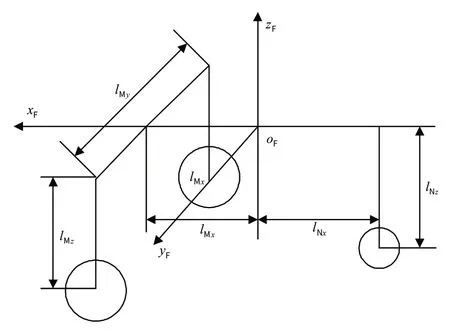
图2 起落架布置示意图Fig.2 Configuration of landing gear

在机身坐标系中，3个机轮底部的坐标分别为：

式（1）～（3）中：下标1、2 和3 分别表示直升机的前轮、左主轮和右主轮；lNx为机身重心到前起落架轴线的距离；lNz为重心到前起落架轮轴的距离；lMx为机身重心到主起落架轴线的距离；lMy为主起落架之间的距离；lMz为重心到主起落架轮轴的距离；rN为前轮半径；rM为主轮半径；s为起落架和轮胎的压缩量。

2.2 起落架的受力

起落架由缓冲支柱和机轮组成。假设不考虑缓冲支柱的摩擦阻尼，则缓冲支柱和机轮均可简化为弹性元件和阻尼元件的并联，单个起落架简化的模型，如图3所示[14-18]。

图3 起落架力学模型示意图Fig.3 Sketch of landing gear mechanical model

起落架受到的力可以表示为：

式（4）中，fxi、fyi和fzi分别表示第i（i=1、2、3）个起落架在x、y和z方向的力。

式（5）～（7）中：ktxi、ktyi、ktzi分别表示轮胎在3 个方向的刚度系数；ctxi、ctyi、ctzi分别表示轮胎在3个方向的阻尼系数；stxi、styi、stzi分别表示轮胎在3 个方向压缩量；kdi、cdi表示起落架缓冲支柱的刚度系数和阻尼系数；sdi表示起落架缓冲支柱的压缩量。stxi、styi、stzi、sdi与直升机姿态及舰船运动有关。

2.3 着舰判断条件

将机身坐标系中3个轮胎底面的坐标转换到惯性坐标系中，然后，再转换到舰面坐标系中，可得3 个轮胎底面在舰面坐标系中的坐标分别为：

式（8）～（10）中：xP、yP、zP为直升机重心在舰面坐标系中的坐标；LSI、LIF分别为惯性坐标系到舰船坐标系、机体坐标系到惯性坐标系的转换矩阵。

如果轮胎底面在舰面坐标系中的竖轴坐标ziP>0，说明该轮胎并未接触舰面；若ziP≤0，说明轮胎开始接触舰面，起落架开始起作用，机体开始受到起落架的作用力。

2.4 起落架压缩量与舰船的关系

假设起落架始终是垂直于机体轴线的，起落架安装点在机体oF-xFyF平面的投影点坐标为：

将上述坐标转换到舰面坐标系中，则有：

式（14）～（16）中，θP、φP为机体相对舰面坐标系的俯仰角和滚转角。

因此，起落架的压缩量分别为：

式（17）～（19）中，HN、HM分别为前、主起落架完全伸展时，轮胎底面与机体xFoFyF面的距离。

3 起落架的动态响应计算与分析

3.1 初始条件

计算的初始条件为：假设直升机在舰面上方3 m处相对飞行甲板静止悬停，此时直升机的前飞速度Va=20 m/s。直升机配平时的姿态角为：滚转角φx=-1.3° ，俯 仰 角φy=1.33°。直 升 机 的 质 量M=9 000 kg。舰船保持不动，初始下沉速度为VzR=1 m/s，直升机旋翼的拉力2 s时线性变化至0。

3.2 计算结果

图4～7是计算所得的结果。图4是直升机在舰面坐标系中，重心高度随时间的变化历程；图5、6是起落架缓冲支柱和轮胎压缩量随时间的变化历程；图7 是直升机的姿态角随时间的变化历程。

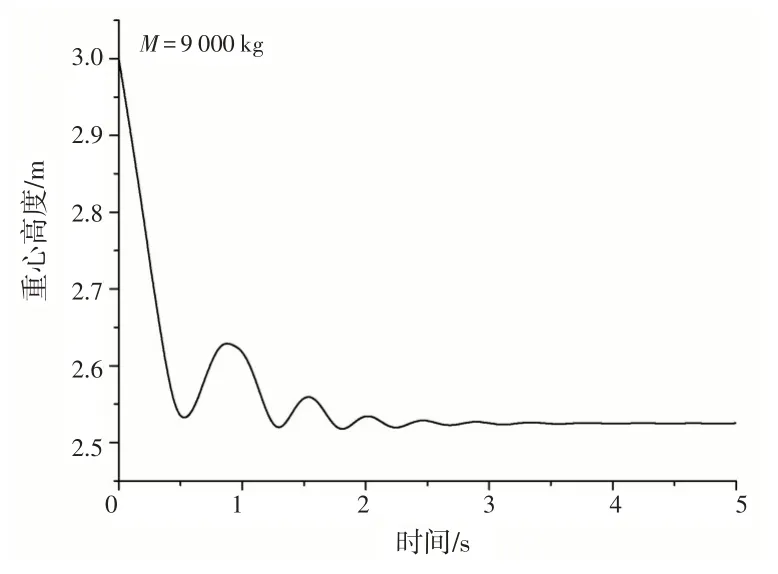
图4 机体重心高度随时间的变化Fig.4 Change of helicopter center of gravity height with time

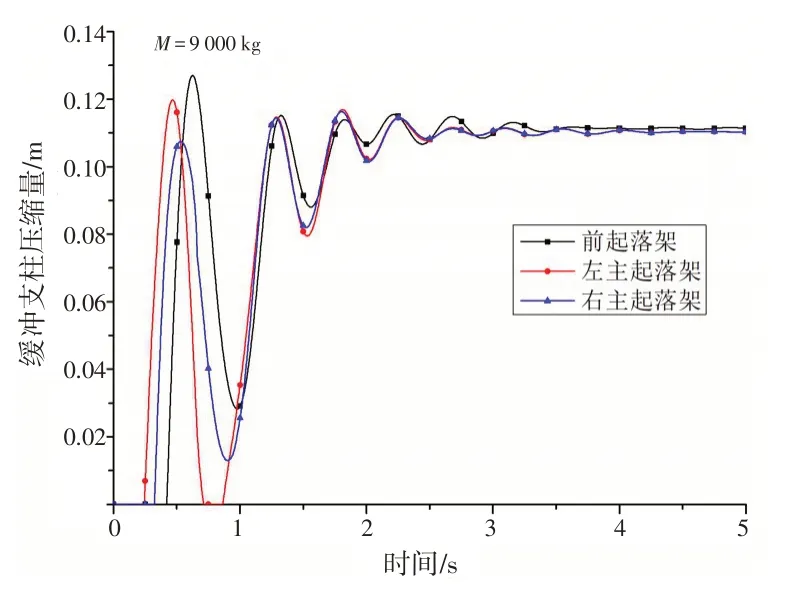
图5 缓冲支柱压缩量随时间的变化Fig.5 Compression of the landing gear damper with time

图6 轮胎的压缩量随时间的变化Fig.6 Compression of the tire with time

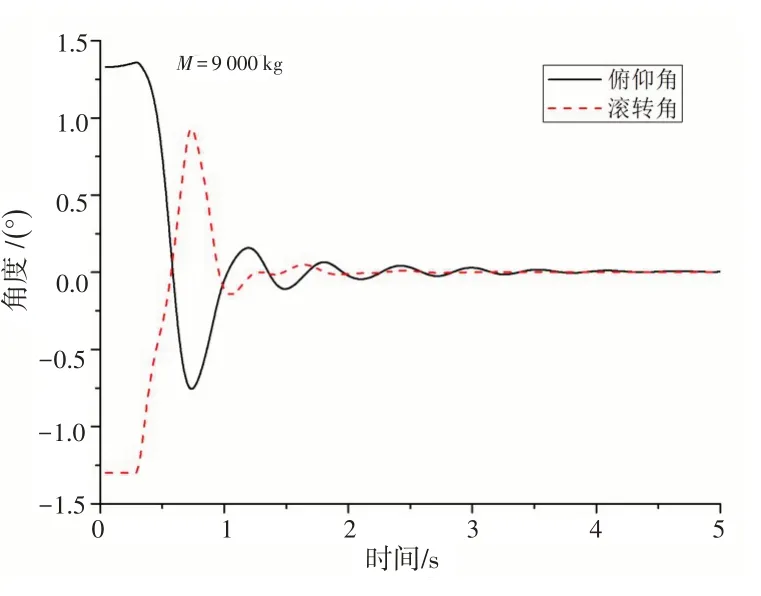
图7 直升机姿态角随时间的变化Fig.7 Attitude angle of the helicopter with time

从图5、6 可以看出，直升机左主起落架最先接触舰面，然后是右主起落架，最后是前起落架着舰。左起落架接舰后出现了1 次弹跳离开舰面，在着舰后各参数迅速衰减，经过约5 s，稳定至平衡位置。前起落架缓冲支柱的最大压缩量为0.13 m；主起落架的最大压缩量约为0.12 m；轮胎的最大压缩量约为0.02 m，均在允许范围内。

3.3 影响因素分析

从着舰质量、着舰姿态、着舰速度3个方面对着舰起落架动态响应的影响进行分析。分析某个因素的影响时，其余参数假定不变。

3.3.1 着舰质量的影响

直升机着舰质量考虑3 种情况：M=9 000 kg ，M=11 000 kg 和M=13 000 kg。以前起落架为例进行说明，图8、9是3种不同着舰质量情况下，前起落架缓冲支柱压缩量和载荷的动态响应。

从图8、9可以看出，3 种不同情况下，直升机都能成功着舰，并且各参数都能迅速稳定，但大质量时稳定时间要长一些。

图8 不同着舰质量下前起落架缓冲支柱的动态响应Fig.8 Dynamic response of the nose landing gear damper with different landing masses

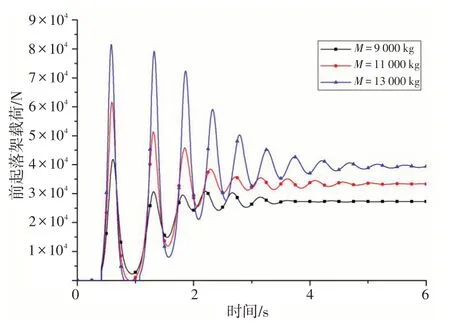
图9 不同着舰质量下前起落架载荷Fig.9 Load of the nose landing gear with different landing masses

计算结果显示，质量增大，起落架缓冲支柱压缩量、载荷等参数的平衡位置均增大，峰值也增大。与M=9 000 kg 时相比，M=13 000 kg 时缓冲支柱最大压缩量增加了0.025 m，轮胎最大压缩量增加了0.014 m，特别是起落架最大载荷增加了1 倍，说明在大质量情况下着舰，机体和起落架面临更大的载荷压力，可能会导致结构的破坏。

3.3.2 着舰姿态的影响

计算初始条件为：直升机着舰质量M=9 000 kg，下沉速度VzR=1 m/s ，相对舰船不动，前飞速度Va=20 m/s，拉力2 s 时减小至0，滚转和俯仰分开考虑。

分析俯仰角的影响时，滚转角初始值φx=-1.3°，俯仰角φy分别取-2°、0°、2°和4°，计算结果，如图10～12所示。

从图10～12 可以看出，俯仰角对起落架的响应有显著的影响：当俯仰角为负时，也就是低头着舰，前起落架会先于主起落架接触舰面，导致前起落架的载荷很大，超出正常着舰载荷92.1%；当俯仰角为正时，直升机主轮先接触舰面，如果俯仰角过大，主轮接触舰面后会造成低头力矩过大，导致前起落架载荷增大。

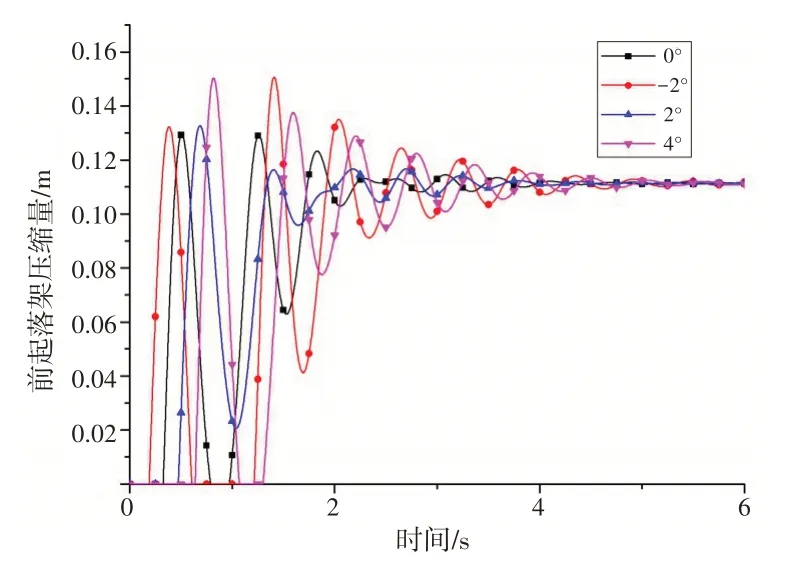
图10 不同着舰俯仰角时前起落架缓冲支柱的动态响应Fig.10 Dynamic response of the nose landing gear damper with different pitch angles

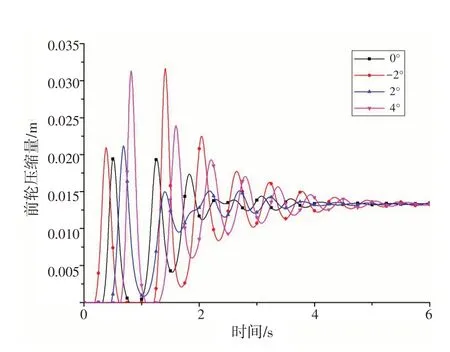
图11 不同着舰俯仰角时前起落架轮胎的动态响应Fig.11 Dynamic response of the nose landing gear tire with different pitch angles

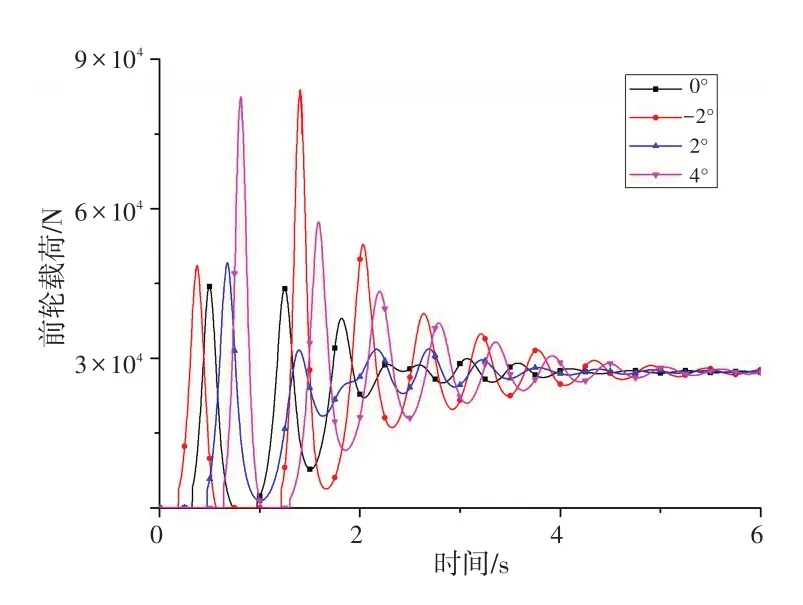
图12 不同着舰俯仰角时前起落架载荷的动态响应Fig.12 Dynamic response of load of the nose landing gear with different pitch angle

分析滚转角的影响时，俯仰角初始值φy=-1.3°，俯仰角φx分别取-1.3°、-4°、-6°和-8°，计算结果如图13～15所示。

从图13～15 来看，滚转角对起落架的动态响应的影响并不十分显著。随着滚转角的增大，缓冲支柱、轮胎的最大压缩量略有增大，起落架载荷有所增大。

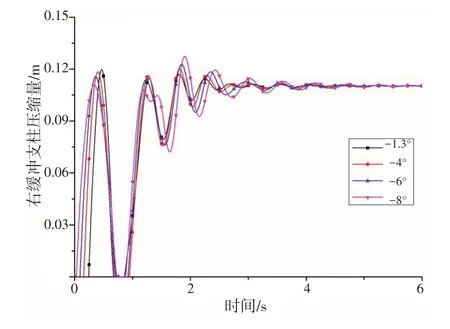
图13 不同着舰滚转角时主起落架缓冲支柱的动态响应Fig.13 Dynamic response of the main landing gear damper with different roll angles

图14 不同着舰滚转角时主起落架轮胎的动态响应Fig.14 Dynamic response of the main landing gear tire with different roll angles

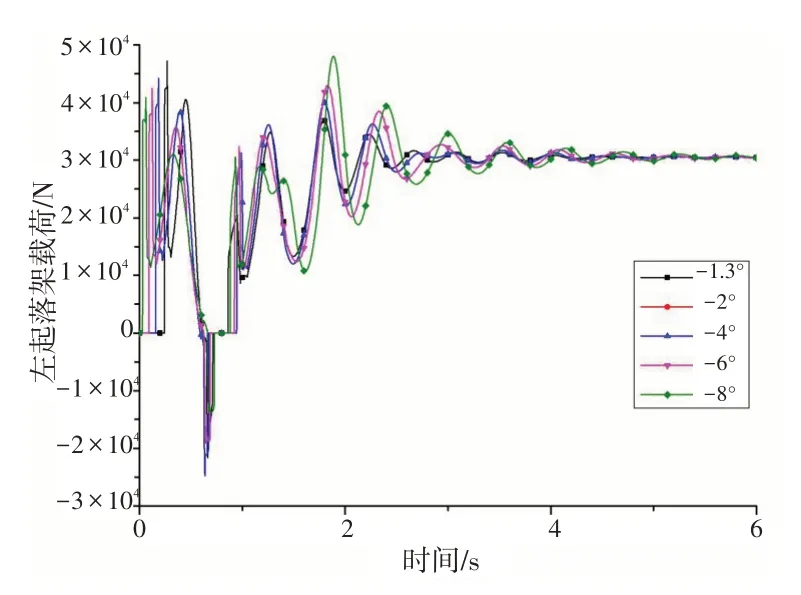
图15 不同着舰滚转角时主起落架载荷的动态响应Fig.15 Dynamic response of load of the main landing gear with different roll angles

3.3.3 着舰速度的影响

计算初始条件为：直升机着舰质量M=9 000 kg，姿态角为滚转角φx=-1.3°、俯仰角φy=1.33°，相对舰船不动，前飞速度Va=20 m/s，拉力2 s时减小至0。

下沉速度VzR取0.5、1、1.5、2 和2.5 m/s 共5 种情况。计算结果如图16～18所示。

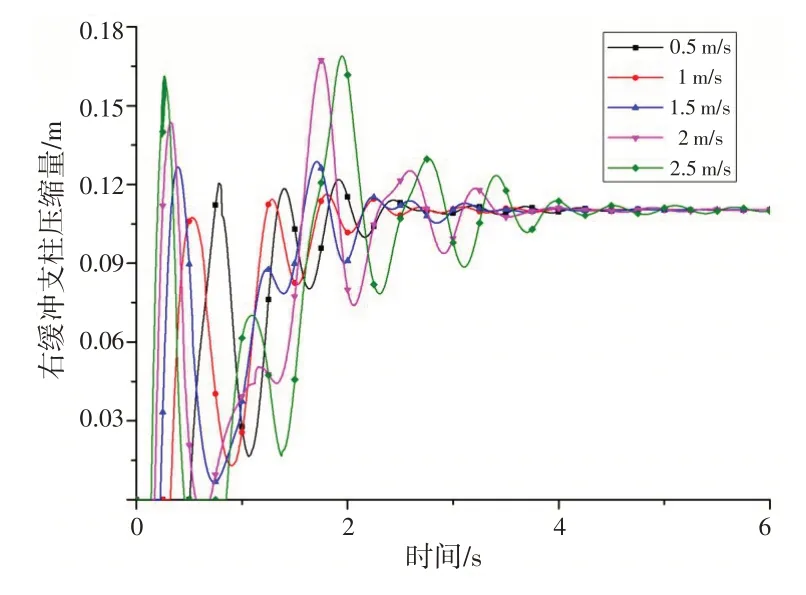
图16 不同着舰速度时主起落架缓冲支柱的动态响应Fig.16 Dynamic response of the main landing gear damper with different landing velocities

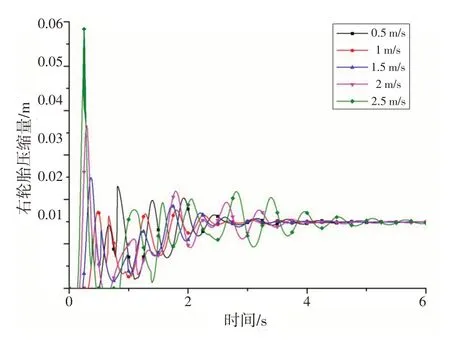
图17 不同着舰速度时主起落架轮胎的动态响应Fig.17 Dynamic response of the main landing gear tire with different landing velocities

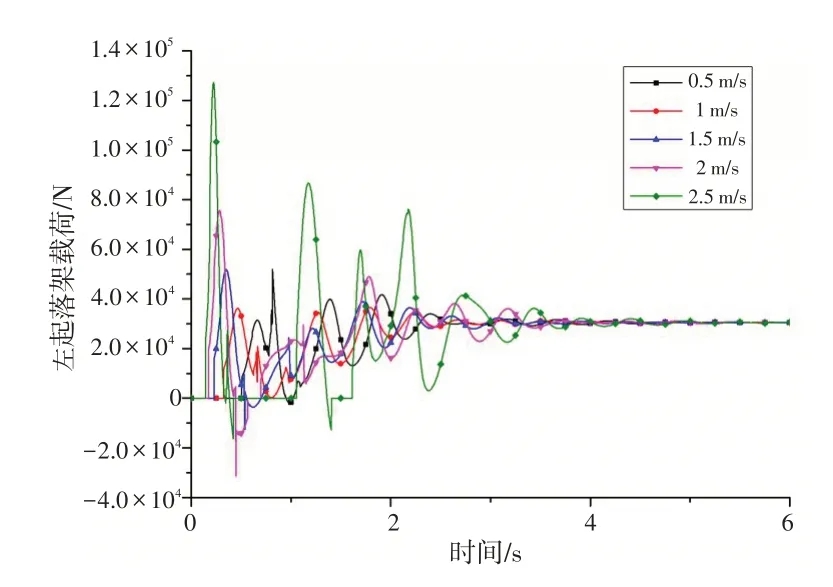
图18 不同着舰速度时主起落架载荷的动态响应Fig.18 Dynamic response of the load of main landing gear with different landing velocities

从图16～18 可以看出，着舰速度对起落架动态响应的影响非常明显：下沉速度越大，起落架缓冲支柱、轮胎的压缩量越大，载荷也急剧增大，特别是当下沉速度超过2.5 m/s时，单个起落架的载荷是直升机自身质量的3倍，严重超出了正常的使用范围。因此，直升机在着舰时，应控制好下沉速度，避免粗暴着舰。

4 结论

本文建立了直升机机体/起落架/舰船耦合的着舰动力学方程，计算分析了直升机着舰时起落架的动态响应，分析了着舰质量、着舰姿态、着舰速度等因素对起落架动态响应的影响，可以得到以下结论：直升机的着舰质量对起落架缓冲支柱压缩量、轮胎压缩量、载荷都有显著的影响，着舰质量越大，压缩量和载荷越大；着舰时直升机的俯仰角对前起落架的影响较大，低头着舰会导致载荷显著增大；直升机的滚转角主要影响主起落架，但不是特别显著；着舰下沉速度对起落架的影响非常大，下沉速度过大会导致着舰载荷急剧增大，对结构造成破坏。