一种新的椭圆球面波信号时频域滤波方法

王媛媛，毛忠阳，陆发平

（1.91001部队，北京 100841；2.海军航空大学，山东烟台 264001；3.91206部队，山东青岛 266109）

0 引言

椭圆球面波函数（Prolate Spheroidal Wave Functions，PSWFs）是Bell 实验室Slepian 和Pollak 于1961年定义的一类特殊函数的集合[1]，具有时域双正交性、时域奇偶性、频谱可控性、在时频域具有最佳能量聚集性等优良特性[2-4]，其被广泛应用于流体力学[5]、目标探测[6]、信号处理[7-10]、通信系统[11-12]、图像处理[13]等领域。在无线电通信领域，得益于PSWFs 的优良特性，基于PSWFs 的非正弦通信，利用PSWFs 信号进行信息传输，具有高信号波形能量聚集性、高系统频带利用率等优良特性，是1 种极具应用潜力和推广前景的非正弦波通信新体制[14-18]。此外，PSWFs 信号作为一类典型的频率时变信号，其各频率分量随时间不断变化。文献[19]引入Wigner-Ville变换，分析了椭圆球面波信号时频域分布特性；在此基础上，文献[20]进一步引入ST 变换、S 变换，分析了Wigner-Ville 变换、ST 变换和S 变换3 种不同时频分析方法下，PSWFs 信号时频域能量分布特性与正交性特点。

由于信号在实际传输过程中，噪声是不可避免的，因此，在接收端，除PSWFs 信号间的影响外，还须要考虑噪声的影响。文献[21]初步探讨了高斯白噪声对PSWFs信号时频域分布的影响。但对于PSWFs信号间的影响，由于PSWFs 信号为非平稳过程，不具备高斯白噪声的平稳特性，因此，PSWFs 信号间的影响可以看作是1种特殊的色噪声影响。如何在时频域滤除干扰噪声（白噪声/色噪声）对PSWFs信号时频域分布特性的影响，目前未有相关文献报道。

针对以上问题，本文引入精细滤波，结合PSWFs信号带宽较宽的特点，构建以距离为依据的滤波算子，在时频域对PSWFs 信号进行时频域滤波，抑制噪声对PSWFs信号时频域分布特性的影响。

1 以距离为依据的时频滤波原理依据

在基于PSWFs的非正弦调制方法中，为实现信息的高速传输，利用频带范围较宽的带通PSWFs信号加载信息，其时频分布大区域区别明显，而小区域区别却不明显。当频带范围为1～7 MHz、时宽为1 μs，相同PSWFs信号间交叉项时频域分布，如图1所示。

从图1可知：

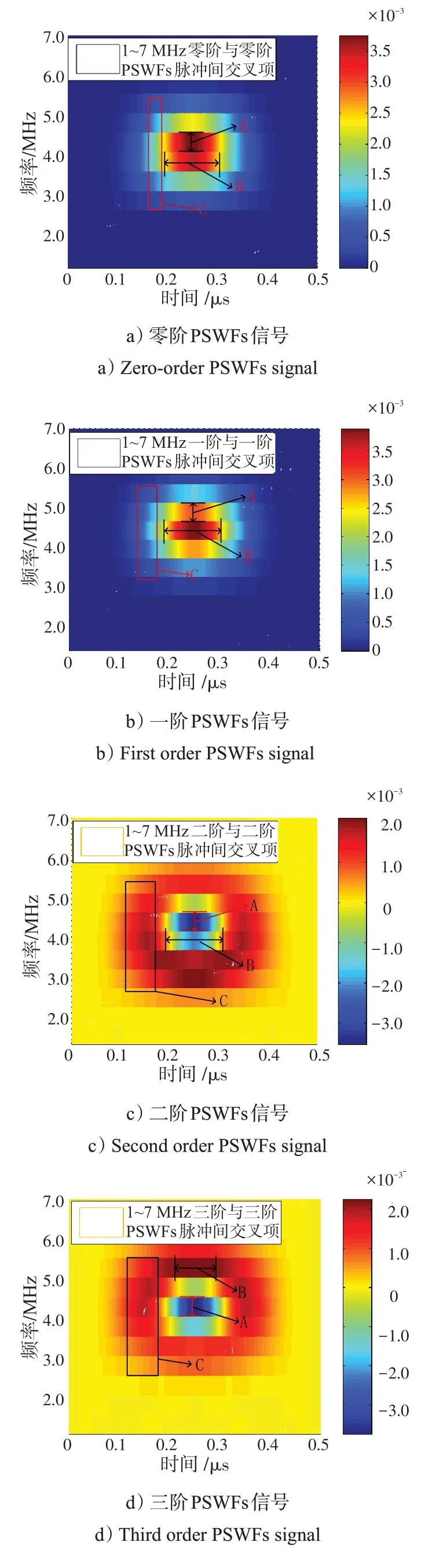
图1 PSWFs信号间交叉项时频域能量密度分布Fig.1 PSD of cross item between PSWFs signals in time-frequency domain

1）PSWFs信号在时频域具有较高的能量聚集度；

2）由图中A 处可知，在不同时刻处，PSWFs 信号在频域的能量分布较为集中，但所占频率范围较宽；

3）由图中B 处可知，在不同频率处，PSWFs 信号在时域的能量分布较为集中，但所占频率范围较宽；

4）由图中C 处可知，在同一时刻，PSWFs 信号在频域的能量分布出现多个能量峰值点。

通过上述分析可知：对于频带较宽的PSWFs信号而言，其时频分布同样表现出能量在时域（频域）持续时间（频率）长的特点；在不同时刻（频率）处，其时频分布极为复杂。

此外，考虑到不同阶PSWFs信号时频域分布在时频面中心位置具有能量峰值，不同时刻（频率）处均拥有各自的能量峰值，因此，构建在时频平面，以能量峰值点为中心。

2 以距离为依据的时频滤波处理流程

考虑到相同PSWFs 信号时频域分布在时频面中心位置具有能量峰值，因此，以时频面能量峰值点为中心（基准），通过计算坐标之间的距离，进而获得滤波算子调节参数α，其获取思路如图2所示。

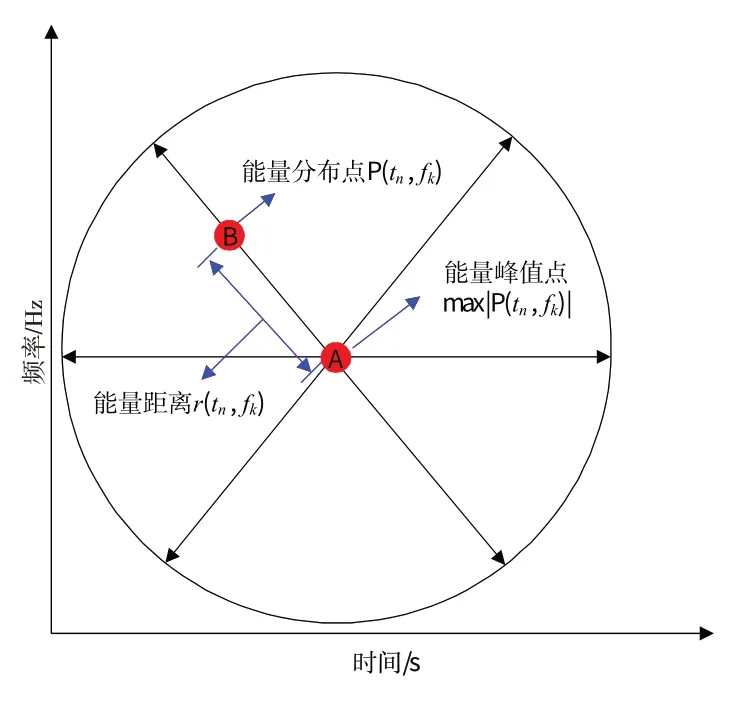
图2 以时频平面能量峰值点为基准Fig.2 Beak point of PSD in time-frequency domain is used as a reference

对信号进行时频滤波的主要步骤。

步骤3：计算时频面能量分布点坐标到(t0,f0)的距离，获取坐标点到能量峰值点距离集合,n=1,2,3,…,N;k=1,2,3,…,K}。

步骤4：计算滤波算子调节参数α，

步骤5：按式（2）计算滤波后的PSWFs信号的时频分布。即：

式（2）中，Pi,j(tn,fk)为离散化的信号交叉项在坐标(tn,fk)处的能量密度值。

3 仿真分析

下面通过计算机进行仿真。考虑到对信号进行时频滤波的目的在于突出有效分量，抑制噪声（干扰）分量，且由式可知，精细滤波是1 种非线性运算，势必会带来一定失真，因此，仿真从原信号时频域分布、添加噪声信号时频域分布、原信号精细滤波后时频域分布以及添加噪声信号精细滤波后时频域分布4 个方面，对时频域平面，以能量峰值点为基准的滤波算子调节参数α，探究其对信号进行时频滤波的有效性。

3.1 仿真条件

1）仿真时选用频率范围1～3 MHz，时宽为1 μs 的PSWFs信号，各阶PSWFs信号的奇偶性，如表1所示。

表1 PSWFs信号的奇偶性Tab.1 Parity symmetry of PSWFs signals

2）噪声类型为高斯白噪声，信噪比为-15 dB。

3.2 仿真结果与分析

PSWFs信号原信号时频域分布、添加噪声后信号时频域分布、原信号精细滤波后时频域分布以及添加噪声信号精细滤波后时频域分布，如图3、4所示。

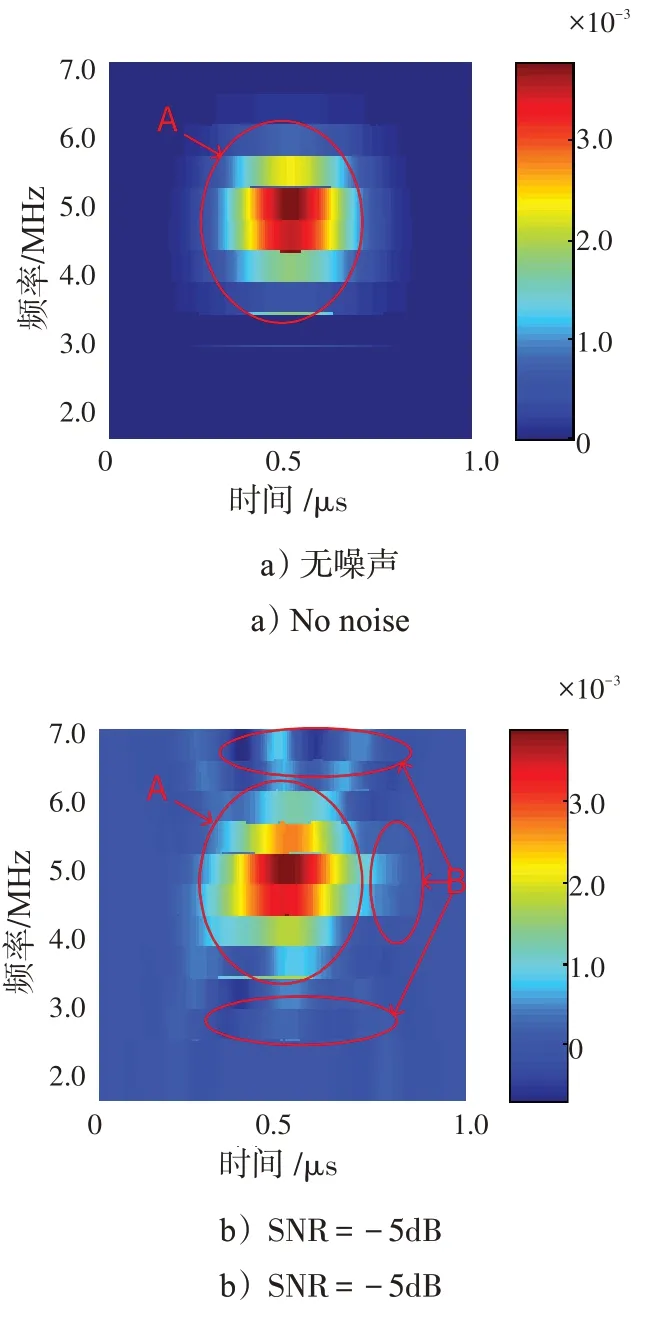
图3 零阶与零阶PSWFs信号间交叉项时频域能量密度分布Fig.3 PSD of cross item between zero-order PSWFs signals in time-frequency domain

图4 二阶与二阶PSWFs信号间交叉项时频域能量密度分布Fig.4 PSD of cross item between second order PSWFs signals in time-frequency domain

从仿真结果得到以下结论。

1）噪声影响PSWFs 信号时频域分布特性。首先，噪声影响PSWFs 信号时频域能量聚集区时频分布。对比图3 b）、4 b）与3 a）、4 a）中A处可知，高斯白噪声会给PSWFs 信号时频域能量聚集区带来一定程度的干扰，导致信号时频域能量存在一定程度的失真。其次，噪声影响PSWFs信号时频域能量聚集区外时频分布。由图3 b）、4 b）中B处可知，高斯白噪声会给PSWFs 信号时频域能量聚集区外带来一定程度的干扰，导致信号在时频域能量聚集区外出现能量分布，影响信号的时频域能量聚集性。

2）精细滤波导致PSWFs 信号发生严重的非线性失真。对比图3 c）、4 c）与3 a）、4 a）可知，精细滤波能够提取出部分PSWFs信号时频域分布特性，如压缩信号在时域能量分布的范围，凸显在中心时刻处，信号在频域的能量分布特性，特别是信号时频域分布能量峰值（图3 c）、4 c）中C处）。通过对比图3 c）、4 c）与3 a）、4 a）中A处可知，其会导致PSWFs信号时频域分布发生失真，部分时频分布特性丢失，特别是除时域中心时刻外，其余时刻时频分布特性的细节信息丢失。

3）精细滤波能够有效抑制噪声对PSWFs信号时频域分布特性的影响。对比图3 d）、4 d）与3 b）、4 b）以及3 c）、4 c）可知，精细滤波能够有效抑制噪声对PSWFs 信号时频域能量聚集区内、外时频分布的影响，提取出在中心时刻处，PSWFs 信号在频域的能量分布特性，降低信号在时频域能量聚集区外的能量分布，提高信号时频域能量聚集性。

4 结论

本文分析了PSWFs信号间交叉项时频分布特性、噪声对PSWFs 信号时频域分布特性的影响，提出了1种新的椭圆球面波信号时频域滤波方法。仿真对比表明，在时频域降低了噪声对信号时频域分布特性的干扰，特别是提取中心时刻处，信号在频域的能量分布特性。值得注意的是，上述滤波效果的获取是以PSWFs 信号部分时频分布特性丢失为代价的。考虑到在不同频率处，PSWFs信号在时域的能量分布较为集中，但所占频率范围较宽。因此，以不同频率/时刻处能量峰值点为基准，构造以距离为依据的滤波算子调节参数，是解决对PSWFs 信号进行精细滤波后，信号的部分时频分布特性丢失问题的1个途径。这也将是我们后续重点关注的研究内容之一。