结合聚类的改进HGS求解复杂车辆路径问题

黄静 王亚彬 白梅娟 闫聚兵 侯帅 王杨洋

关键词：车辆路径问题；多供应方；时间窗；聚类分解；改进饥饿游戏搜索算法

车辆路径问题（VRP）是在1959 年由Dantzig 和Ramser首先提出[1]，自提出后便受到众多学者来深入研究。典型的车辆路径问题往往只存在一个供应方，多供应方车辆路径问题（MDVRP）即存在多个供应方，通过合理的路径优化，将需求地分配给确定供应方，并由供应方分配车辆来完成配送。

近年来部分研究提出了一些分解策略[2-5]，将MDVRP分解为一系列子问题（单供应方VRP） ，再求解该子问题。例如，陈诚等人[6]通过基于边界客户分配法的转化策略把MDVRP转化成单供应方VRP，再用禁忌搜索算法对单供应方VRP 进行路线规划[7]。Ma等人使用全局搜索集群将问题转化为多个单供应方的多目标优化问题，然后设计了一个多目标遗传算法来解决转化的VRP[8]。郑建辉等人[9]通过最近距离分配原则来转化多供应方问题，再根据禁忌搜索算法进行优化求解。史春燕等人[10]根据k-means聚类算法将多供应方VRP转化为单供应方VRP，然后利用模拟退火算法进行求解。胡蓉等人[11]先用两种基于Kmeans的聚类将原问题分解成若干子问题，再设计一种增强蚁群算法来求解。上述文献对MDVRP的分解主要是根据需求地的密度或距离信息。而在其分解结果平衡性方面的研究目前还较少。然而对于MDVRP_TW问题，由于其求解难度较高，截至目前，在MDVRP_TW问题上获得的成果仍是比较有限的，故开展相关研究意义重大。

本文提出了一种结合聚类分解策略的改进饥饿游戏搜索算法（Improved Hunger Games Search Algo?rithm Based on Cluster Decomposition， IHGS_CD），首先本文结合MDVRP_TW的特征，设计了求解该问题的改进饥饿游戏搜索算法（IHGS）。饥饿游戏搜索算法（Hunger games search，HGS）[12]是一种按照动物饥饿驱动活动和行为而设计的新型智能优化，具备寻优能力强、收敛快等特点。截至目前，还尚未有文献将HGS应用于MDVRP_TW的求解。其次基于K-means的平衡约束聚类算法（BCGS）的思想使得各供应方的资源划分更具平衡性。最后提出的改进饥饿游戏搜索算法，采用个体精度约束参数来控制个体继续迭代，能有效提高个体精度。

1 MDVRP_TW 建模与分析

MDVRP_TW属于带软时间窗约束的多供应方车辆配送问题，优化目标为最小化配送总成本。

1.1 问题假设和符号定义

MDVRP_TW满足如下假设：

（1） 供应方和需求地的位置坐标已知；

（2） 车辆送完货后需返回原供应方；

（3） 车辆为同种车型，且容量已知，在配送过程中不得超过其额定载重量；

（4） 配送需尽量在各需求地设定的时间段内完成。

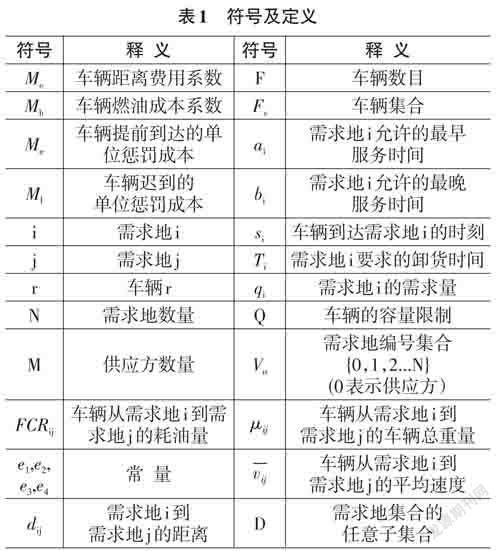
MDVRP_TW的相关符号定义如表1所示：

1.2 问题优化目标计算模型

MDVRP_TW的优化目标为配送总成本H，该优化目标由两部分组成：车辆经济成本H1和软时间窗惩罚成本H2。H1和H2的计算公式如式（1） 和（2） 所示：

1.3 问题模型

问题优化目标：

式（6）表示最小化配送总成本；式（7）表示容量限制约束，即分配给车辆的货物量不能超过车辆的额定载重；式（8）代表所有车辆从某供应方出发且都回到该供应方；式（9）表示车辆驶入需求地，也会从其驶出；式（10）表示需求地间没有子回路；式（11）表示从某供应方出发的车辆数和回到该供应方的车辆数相等。

2 问题求解算法IHGS_CD

本文提出的IHGS_CD由问题分解阶段和子问题求解阶段组成。其结构如图1所示。

2.1 IHGS_CD 的问题分解阶段

IHGS_CD的问题分解阶段执行BCGS[13]，用于将原问题MDVRP_TW 分解为Gt 个单供应方子问题VRP_TWs。

随着需求地数量逐渐增大，聚类后会出现各供应方服务的需求地数量相差较大。为确保各供应方的需求地资源能平衡划分，采用BCGS进行聚类，根据对簇可以包含的数据点个数进行限制，可更合理地分配各供应方所服务的需求地群。BCGS步骤如下：

Step1 对每个需求地进行K-means聚类。初始化簇数目为供应方数目K，初始化簇可以包含的数据点个数上限为u，初始化簇中心为每个供应方的坐标位置，评价指标为欧式距离和u，终止条件为簇不发生变化或达到最大迭代次数。

Step2 将需求地ni分配至合适的供应方。计算ni与各簇中心点的距离，按照由近到远排序后存入Q={mj|j=1，2，3，...，K}中。然后，按照由近到远顺序尝试加入Q 中的某一个簇中。

Step3 平衡需求地群。如果供应方mj簇中当前需求地个数未达到u，则将需求地ni加入簇mj中。但若簇mj中当前需求地个数已达上限，则需比较簇mj当前边界需求地nb离中心点的位置与ni离簇mj中心点的位置。若ni离中心点更近，则将簇mj中的当前边界需求地nb移出该簇mj，然后将需求地ni加入簇mj中。且对nb （边界需求地即簇中与中心点距离最远的需求地）进行重新分配。否则用相同的策略尝试将ni加入簇mj+1中，直到ni成功添加至某个簇。

Step4 当簇不发生变化或达到最大迭代次数时，则输出各供应方服务的需求地群。

2.2 IHGS_CD 的子問题求解阶段

本阶段采用设计的IHGS依次对每个VRP_TW进行求解，进而可获得原问题的解和优化目标值。

2.2.1 编码与解码规则

本文采用的自然数编码[8]。每个个体代表多辆车。

IHGS采用贪心策略对每个个体的配送路径进行解码，在不违背载重约束的情况下，根据个体从左往右的顺序将需求地插入当前车辆。如果添加下一需求地，当前车辆将违反载重量约束，则应分配下一辆车来服务剩余需求地。

2.2.2 适应度函数

适应度对于评价个体位置的优劣和对个体进行位置更新操作有着重要作用。最优的个体Xbest即是适应度最高的种群个体。因本文所设的目标函数为配送总成本，故可将种群个体的适应度设成与配送总成本成反比关系的值，即当配送总成本越小，该种群个体的适应度越高，反之则相反。则适应度函数设置如式（14） 所示：

H 代表当前个体所求得的配送成本，min（H）代表最小配送成本值，max（H）代表最大配送成本值。

2.2.3 接近食物

X（t）为第t 代个体位置，t 是迭代次数，rn（1）是一个满足正态分布的随机数，c1和c2均是范围在[0，1]的随机数，h 是一个可以改善算法性能的控制参数，G1和G2指的是饥饿的权重，Xbest代表全局最优位置。P 为在[-a，a]范围内，用于控制活动范围的参数公式如式（16） 所示：

2.2.4 饥饿角色

模拟搜索中个体的饥饿特征为：

Z 代表个体数量，hg（i）表示个体的饥饿程度，Shg是全部个体饥饿程度的总和。c3，c4和c5均是范围在[0，1]的随机数。

在每次迭代中，当个体适应度与最佳适应度相同时，将个体的饥饿值设置为0。否则，在原始饥饿值的基础上增加一个新的饥饿值hgn，每个个体对应不同的hgn。hgn的公式如式（23） 所示：

2.2.5 算法步骤

根据前面对接近食物和饥饿角色的描述，可将整个算法流程描述如下：

Step1 初始化参数。

个体总数量N，最大迭代次数T，参数h，全部个体饥饿程度的总和Shg，个体精度约束参数f。

Step2 初始化个体Xi的位置。

Step3 判断迭代次数是否大于T，如果是，则输出全局最优解，否则，继续执行Step4。

Step4 依照式（14）计算所有个体的适应度值，更新Fitbest，Fitworst，Xbest，分别依照式（20）式（21）计算饥饿权重G1和G2，依照式（18）计算M，依照式（16）更新P，依照式（15）更新个体。

Step5 依照式（14）计算更新的个体适应度值，若Fit

Step6 t=t+1，返回执行Step3。

3 实验比较与分析

为验证所提算法的有效性。本文通过Python程序对算例进行仿真实验。

算例：设在一个边长为35km的正方形区域里有3个供应方和30个需求地，每个供应方均配备4台车辆，且每辆车的空车重量为5 000kg，平均速度为30km/h，车辆的最大负载均为11t。要求车辆配送路线合理，使之取得最短配送总长度。

设置最大迭代次数T=100，改善算法性能的参数h=0.03，个体精度约束参数f=0.3，搜索空间的上限BU=100，下限BL=100，惩罚成本Me=10元/小时，Ml=15元/小时，Mc=1.2元/km，Mh=6.8元/L。

表2给出了应用本文设计的IHGS_CD求解到的最优配送路线与应用结合最近距离分配的禁忌搜索算法的求解结果比较，验证了本文算法的有效性。其中，禁忌搜索算法的参数设置为：不可行路徑惩罚权重为300km，迭代次数为400，每次迭代搜索当前邻居个数为40，禁忌长度为20。通过对比可得，应用本文设计的IHGS_CD 对算例求解，得到的最优结果为140.14km，与应用最近距离分配结合禁忌搜索算法得到的145.76km相比也有很大提升。此外，本文算法在求解过程中确保每个供应方的需求地资源能平衡划分。据此可以看出，IHGS_CD在求解带时间窗多供应方车辆路径问题上具有良好效果。

4 结论

针对MDVRP_TW，本文提出一种结合聚类分解策略的改进饥饿游戏搜索算法进行求解。其中，该问题分解阶段采用的BCGS能使得需求地资源平衡划分给供应方，并有效控制问题规模且快速引导算法在较优区域内搜索，求解阶段采用IHGS对每个分解后的子问题VRP_TW进行求解，IHGS引入个体精度约束参数来控制个体继续迭代，从而有效控制个体精度以提高算法的全局最优解。本文所提方法与结合最近距离的分配禁忌搜索算法相比，取得了较好的预测效果。同时，验证了改进饥饿游戏搜索算法求解MDVRP_TW的有效算法，拓宽了其实际应用领域。