不同前缘形状非细长三角翼等离子体流动控制的参数影响实验

李 昌, 赵光银*, 于文涛, 张 鑫

(1.中国空气动力研究与发展中心空气动力学国家重点实验室, 四川绵阳,621000;2.中国空气动力研究与发展中心低速空气动力研究所, 四川绵阳,621000)

现代战斗机由于对高速和高机动性的要求,较多采用三角翼布局,然而大迎角状态下三角翼绕流发展为脱体涡流型,其空气动力特性受前缘涡结构影响较大,同时前缘形状、雷诺数、迎角均对三角翼前缘涡的稳定性、破裂等有显著影响[1-7]。

通过流动控制手段能够有效控制三角翼绕流中分离流和旋涡,推迟三角翼大迎角下涡破裂或者增强涡强度,可提高机翼稳定性和改善升力特性[8-13]。等离子体气动激励具有响应快、结构简单、频带宽等优点,在分离流和旋涡控制领域有一定发展潜力[14]。

国际上三角翼等离子体流动控制研究仍处于初步探索阶段,现有研究中多采用AC-DBD等离子体激励[1],其中主要有4种DBD等离子体激励器布局用于三角翼前缘涡控制的探索研究:①激励器布置在机翼前缘,由脉冲式放电引入的前缘非定常扰动比连续式放电控制效果好[15-16];②激励器垂直于前缘布置以诱导附面层向下游加速,定常连续放电激励效果比非定常脉冲激励效果好,逆气流方向的连续激励可导致旋涡提前破裂[17];③激励器沿二次分离线布置,研究认为这种布局下的非定常激励对旋涡的稳定性有一定控制效果[17];④激励器布置在上翼面不同弦向或垂直于翼根的位置,以诱导流动顺涡轴方向加速[18-19]。以上研究主要以尖前缘三角翼为研究对象,此时分离点被固定在前缘处,然而实际中的飞行器前缘常为钝前缘结构,因此将流动控制技术应用于钝前缘机翼的研究更有意义。

相关研究表明,在同样来流条件和后掠角下,三角翼的不同前缘形状会对涡运动产生很大影响,相对于尖前缘三角翼,钝前缘三角翼的涡流特性由于前缘黏性效应而更为复杂,其前缘涡分离点位于前缘下游[3]。前缘涡特性的差异会影响流动控制效果,因此有必要研究揭示等离子体气动激励对不同前缘形状三角翼绕流的控制规律和机理。

1 实验设置

1.1 风洞

实验在中国空气动力研究与发展中心的FL-11风洞中完成,实验段尺寸为1.8 m(宽)×1.4 m(高),模型中心距实验段入口2.6 m,稳定风速范围为10～105 m/s,当风速低于70 m/s时湍流度达到0.000 8。本文中实验风速固定为50 m/s。

1.2 实验模型

实验模型为3个不同前缘形状的翼-身组合体,其机翼是45°后掠角的三角翼,机翼展弦比为2,厚度10 mm,迎角45°时形成的风洞阻塞度为2.53%,其他参数见表1。模型如图1～2所示,其中尖前缘机翼为WingSLE,圆前缘机翼为WingCLE,椭圆前缘机翼为WingELE。模型主要部件包括机身、机翼、整流盖板、天平套筒等,均采用树脂材料通过3D打印制成,加工精度为0.05 mm。模型通过机身内嵌套筒与天平配合。

表1 模型参数表

1.3 激励系统

激励系统主要包括等离子体激励器和高压电源。其中等离子体激励器构型如图3所示,包括激励器电极和绝缘介质层。激励器电极由厚度0.02 mm的铜箔制成,其中高压电极宽度为5 mm;低压电极宽度为10 mm;绝缘介质层为0.2 mm厚度的聚酰亚胺胶带,介电常数为3.4。

(a)Wing SLE (b)Wing CLE (c)Wing ELE

图3 介质阻挡放电等离子体激励器布局图

相关研究表明,布置于前缘的激励器对于非细长三角翼的控制效果优于其他布局[20],为此本文设计了Type A和Type B两种前缘激励器布局研究其对于三角翼气动力特性的影响,其中Type A激励器能够产生从前缘顶点指向上翼面的等离子体,Type B激励器则产生从前缘顶点指向下翼面的等离子体。以圆前缘三角翼模型为例,图4给出了激励器布置示意图,高压和低压电极的间隙为0。

(a)Type A激励器

使用的脉冲等离子体电源为CTP-2000K,功率为500 W。输入为0～220 V、50 Hz的交流电,输出为脉冲频率(1～1 000 Hz)、载波频率(5～20 kHz)和输出电压(0～30 kV)能在一定范围内连续可调的正弦波。该电源为稳电压输出,电压(U)调节至特定值后,输出端电流(I)可以通过电源自带的电流表读取(波动量0.01 A),电源输入功率P=UI测量的相对误差为1%。

等离子体激励器有2种工作模式:定常激励与非定常激励。图5给出了AC-DBD等离子体定常和非定常激励的波形图。定常激励时,加载电压波形为连续的正弦波,激励器可诱导产生准定常的近壁面射流;非定常激励则是带占空比的周期性脉冲放电,激励器可诱导产生非定常的近壁面涡流扰动。此时关键参数为占空比τ和脉冲频率f,其中脉冲频率f根据平均气动弦长l和来流速度u∞进行无量纲化,定义无量纲脉冲频率f+=fl/u∞,通过无量纲脉冲频率f+有利于获取非定常扰动对流动控制效果影响的普遍规律。

图5 激励器定常和非定常工作模式示意图

本文中实验工况见表2。

表2 实验工况表

1.4 测试设备及方法

1.4.1 风速管

使用T4-800型风速管获取实验参考速压,风速管安装于实验段上游远离翼型截面的位置,从而降低对翼型周围流场的干扰。

1.4.2 实验天平

采用TG0203A应变天平测力。天平的浮动端与模型相连,固定端与支撑装置连接。为避免AC-DBD激励对天平测力带来电磁干扰,天平与激励系统的电源线、信号线分开接地,同时采取同轴电缆等屏蔽措施。

1.4.3 数据采集系统

采用PXI 总线数采平台采集天平数据。该平台主要由前置放大器、数据采集器、通讯卡、控制计算机和数据处理计算机等部分组成,并配套编写相应的数据采集和处理程序。

1.4.4 油流实验方法

油流法是一种简单有效的流动显示方法,采用滑石粉、机油、液态蜡配制为混合试剂后均匀涂抹于模型上表面,具体配比根据现场温、湿度条件进行调整。在风洞上方使用摄像机记录模型表面油流图谱。

2 实验结果与讨论

首先进行AC-DBD激励对测量系统电磁干扰的排除实验和天平测力重复性实验,均在圆前缘三角翼模型上进行。实验中通过采用同轴电缆和良好接地等措施有效消除了电磁干扰,在升力方向加载20 N力的条件下,对比了激励器关闭、定常激励(Up-p=12 kV,f=5.239 Hz)、非定常激励(Up-p=12 kV,f+=1.0,τ=30%)的升阻力测量结果(见图6),可知测力结果的重复性和稳定性良好。另外实验前对所用天平的测力进行了5次重复实验,升力系数(CL)和阻力系数(CD)测量相对误差均小于5%(见图7)。

图6 电磁干扰排除结果

(a)升力系数

2.1 干净模型的气动特性

在风速50 m/s条件下开展了干净(无激励器)模型的测力实验,结果如图8所示。对于相同后掠角,不同前缘形状的三角翼,其气动特性表现出明显差异。两种钝前缘三角翼的失速迎角均大于尖前缘三角翼,这与文献中研究结果一致[3]。

(a)升力系数

在小迎角状态下,尖前缘三角翼的升力系数略高于钝前缘机翼的升力系数。这是由于相较于其他两种钝前缘三角翼,尖前缘的前缘剪切层会更早分离产生前缘涡,前缘涡为机翼提供了额外的涡升力[21-22]。

对圆和椭圆两种钝前缘的三角翼,两者在较低迎角下(α<5°)的升力系数曲线基本重合。随迎角增大,圆前缘三角翼的升力系数明显高于椭圆前缘,其失速迎角也最大。

对于阻力系数,钝前缘三角翼的阻力系数在迎角约22°以下均明显低于尖前缘三角翼的阻力系数。从升阻比上来看,2种前缘形状三角翼的最大升阻比出现在4°～7°小迎角状态下。其中椭圆前缘机翼最大升阻比可达到9。尖、圆、椭圆3种不同前缘形状三角翼最大升阻比对应的平均升力系数为CLS= 0.33,CLC= 0.30和CLE= 0.41(下标S-尖前缘,C-圆前缘,E-椭圆前缘)。迎角达到10°之后,3种前缘形状三角翼的升阻比变化趋势一致,圆形前缘三角翼的升阻比最大。

前缘形状对三角翼的基准气动特性产生了明显的影响,其原因与前缘涡的形成与发展紧密相关。

2.2 激励器布局影响

为了研究AC-DBD激励器的最佳作用位置,基于Type A 和Type B两种激励器下,开展了圆前缘三角翼流动控制的测力实验。实验速度50 m/s,激励电压峰-峰值Up-p=12 kV,占空比τ=30%,对应模型基于平均气动弦长的雷诺数Re=0.64×106,无量纲脉冲频率f+=fl/u∞=1.0(对应的脉冲激励频率为250 Hz)。激励前后不同迎角下升阻力变化量如图9所示。

(a)升力系数变化量

Type A 和Type B两种激励器均能取得一定的控制效果,在失速之前,Type A激励器对升力系数的增加量更显著。失速之后则Type B激励器效果更优。这可能与失速前后三角翼绕流特性的变化有关,对于非细长三角翼,在迎角不大时,前缘分离剪切层在机翼内侧又附着于翼面上,流态如图10(a)所示;而随着迎角增大,附着点内移,在临界迎角时移至翼根,这意味着即将失速,失速后的剪切层附着点脱离翼面[23],流态如图10(b)所示。

(a)非细长三角翼上附体 (b)三角翼上非附体

2.3 激励参数的影响

2.3.1 激励方式的影响

在3种前缘形状三角翼前缘敷设Type A激励器,采用定常激励和非定常激励两种激励方式开展流动控制研究,激励电压峰峰值Up-p=12 kV,载波频率f=5.294 kHz,非定常激励下无量纲脉冲频率f+=1.0,占空比τ=30%。激励前后不同迎角下三角翼气动特性见表3和图11～13。

表3 AC-DBD激励控制前后三角翼的气动特性

(a)升力系数

(a)升力系数

(a)升力系数

对于圆前缘三角翼,前缘AC-DBD的2种激励方式均可推迟失速迎角,并同时提高升力系数和阻力系数,非定常激励作用效果更好;对于尖前缘三角翼,前缘AC-DBD激励仅在失速迎角之后起作用,且对升力系数和阻力系数的改善不明显,非定常激励作用效果相对较好;对于椭圆前缘三角翼,AC-DBD激励的作用效果介于圆前缘和尖前缘三角翼之间,在失速迎角前后均能提高气动特性,但是作用效果有限,且无法推迟失速迎角。

定常激励可产生使流体向下游加速的近壁面切向体积力,实验证明这种方式并不能有效提高三角翼气动特性;而同样激励电压下的非定常激励则是通过对前缘剪切层产生扰动来起作用的。非定常激励的控制效果明显优于定常激励,说明AC-DBD前缘激励控制非细长三角翼的主要原理是利用激励或扰动的非定常性激发剪切层的不稳定性进而达到流动控制的目的。

根据尖前缘三角翼上表面油流的运动录像,画出壁面流线如图14所示,在α=16°时三角翼还未失速,但是机翼上已经出现了大面积的回流,前缘涡破裂位置已经发展到接近前缘顶点。施加非定常激励后,破裂点向下游移动。

图14 非定常激励前后三角翼上翼面油流图谱(Up-p=12 kV,f+=1.0,τ=30%,α=16°)

2.3.2 脉冲频率的影响

脉冲频率是衡量激励非定常性的一个重要参数。相关研究表明,适当频率的非定常扰动能够激发剪切层K-H不稳定性,促进分离剪切层附体[1]。

在Type A激励器作用下,对不同形状前缘的三角翼研究了脉冲频率对控制效果的影响。实验风速50 m/s,激励电压峰峰值为Up-p=12 kV,占空比30%,迎角为24°。取无量纲脉冲频率f+=fl/u∞=0.5、1、2、3、4,对应的脉冲激励频率分别为125 Hz、250 Hz、500 Hz、750 Hz和1 000 Hz,测力实验结果见图15。同时图16给出了电源的输出功率,由于不同前缘形状三角翼的激励器相同,仅列出一组激励器对应的电源输出功率。

(a)升力系数

α=24°时,不同脉冲激励频率的控制均取得了一定控制效果。对于尖前缘三角翼,无量纲脉冲频率f+=1时控制效果最佳,升力系数增大2.6%;对于圆和椭圆前缘三角翼,最佳无量纲脉冲频率为f+= 2,升力系数分别提高了5.5%和1.8%。以上结果表明,对于45°后掠角三角翼,非定常激励的最佳无量纲脉冲频率f+=1～2,这与文献中的其他非定常流动控制手段的控制规律一致[24]。普遍认为该脉冲频率有利于激发剪切层的不稳定性。在脉冲调制过程中,由于输出电压的载波频率保持不变,此时随脉冲频率(调制频率)变化,激励器功耗基本一致。

2.3.3 占空比的影响

非定常AC-DBD等离子体激励的占空比同样是衡量非定常性的重要参数,在占空循环作用下激励可诱导产生一系列诱导涡。同时,固定脉冲频率时,占空比决定了一个周期内等离子体激励的作用时间。在实验风速50 m/s,激励电压峰峰值Up-p=12 kV,无量纲脉冲频率f+=1时,研究了Type A激励器工作占空比对三角翼气动特性的影响,实验结果见图17～18。

(a)升力系数

图18 不同占空比下电源输出功率(Up-p =12 kV,f+=1.0)

占空比为5%的激励,控制效果最佳;占空比越大,升力系数增量越小,且5%占空比的非定常激励对圆前缘三角翼的作用效果最好。在迎角24°,占空比5%时:尖前缘三角翼升力系数增大了3.6%,阻力系数增大了2.8%;圆前缘三角翼升力系数增大了5.9%,阻力系数增大了5.2%;椭圆前缘三角翼升力系数增大了4.2%,阻力系数增大了3.3%。从图17看出,占空比5%对三角翼气动特性的控制效果最好,且此时电源所耗的功率最低。进一步表明,AC-DBD等离子体激励对45°后掠角三角翼流动的主要作用机理在于非定常扰动。

2.3.4 电压的影响

非定常AC-DBD等离子体激励强度与激励电压直接相关,激励电压越高则扰动强度也越大,进而能够获取更好的控制效果。固定无量纲脉冲频率f+=1.0,占空比τ=30%,通过改变激励电压开展Type A激励器对尖前缘和圆前缘三角翼气动特性的影响研究。

图19给出了施加不同电压激励后模型的升阻力系数。对于45°后掠角的尖前缘和圆前缘三角翼,前缘非定常AC-DBD激励对升阻力系数的改善效果随激励电压增大而增强,在Up-p=14 kV时,2种前缘形状三角翼在24°状态下的升力系数分别增加了2.7%和7.3%,阻力系数分别增加了2.1%和5.7%。文献[25]认为,等离子体激励在翼型分离控制上存在一个阈值电压,即激励电压高于阈值电压后,分离得到完全控制。本文中对45°圆前缘三角翼研究时,在目前施加的电压范围内(7～14 kV),还没有观察到明显的阈值电压,电源的输出功率随激励电压增大而不断增加(见图20)。脉冲AC-DBD激励的瞬间强度还有待提升,发展高强度的短脉冲激励更有优势。

(a)升力系数

图20 不同电压下电源输出功率(f +=1.0,τ=30%)

2.4 控制机理探讨

对于非细长三角翼,失速主要是由于剪切层流动脱离翼面导致的,过失速阶段翼面上难以附着形成稳定的前缘涡而存在大面积的分离区,此时前缘形状的不同会导致分离点位置和分离角度存在差异。钝前缘三角翼的分离点位于上翼面前缘稍向下游,剪切层分离角相对较小,易于控制;尖前缘三角翼的分离点固定在前缘,剪切层的分离角度相对较大[15],受控之后附着难度较大。另外,可从流体动能(定义为Ek=(U2+V2+W2)/2)的角度分析,前缘曲率不同影响前缘流速分布。在同样来流条件下,圆前缘处的流体动能明显大于尖前缘处,这是由于在曲率较小的圆前缘处,气流局部加速明显,速度相对较大;尖前缘处,在前缘顶点附近气流无明显加速而直接分离,如图21(a)和图22(a)所示。

(a)激励前

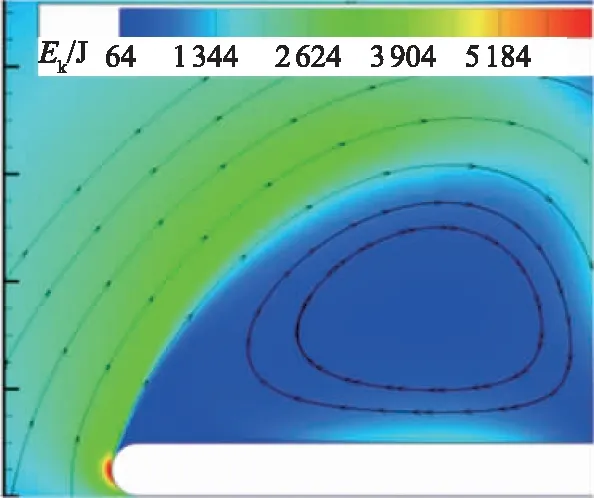
(a)激励前

AC-DBD等离子体激励能够在三角翼前缘引入非定常扰动,促进局部气流掺混。其中位于尖前缘处的激励虽然促进了掺混,但是前缘剪切层主流侧的动能相对较低,掺混效果有限,产生的诱导流向涡强度较低,弱的流向涡沿分离剪切层运动,最终被分离涡吞没,见图21(b)。而位于圆前缘处的激励则能够更好的将高动能流体引入分离区,促进局部对流,使剪切层失稳产生较强的诱导流向涡,强的诱导流向涡发展成为附着的前缘涡,见图22(b)。不同曲率前缘处施加非定常激励,诱导出不同的流向涡结构,从而导致控制效果的不同。

3 结论

本文采用AC-DBD等离子体激励,对具有不同前缘曲率的45°后掠非细长三角翼模型开展流动控制实验研究,主要结论如下:

1)小迎角状态下,尖前缘三角翼的升力系数略高于钝前缘三角翼;圆和椭圆两种钝前缘三角翼的失速迎角基本一致,均比尖前缘三角翼大,圆前缘三角翼能够达到的最大升力系数最高。

2)指向上翼面的前缘激励在失速迎角之前的控制效果更好,指向下翼面的前缘激励则在失速迎角之后效果更佳。

3)不同前缘形状的非细长三角翼流动控制效果存在明显差异。圆前缘三角翼的控制效果明显优于尖前缘和椭圆前缘,相同激励电压下(12 kV),激励控制对尖、圆和椭圆前缘三角翼在过失速阶段的升力分别可提高3.6%、5.9%和4.2%。

4)非定常激励能够有效改善三角翼升力特性,并推迟上翼面涡破裂位置;AC-DBD控制非细长三角翼的主要机理是其对剪切层的非定常扰动,最优的无量纲脉冲频率f+=1～2;最优占空比τ=5%,扰动强度对应的激励电压越高,控制效果越好。

5)限于电源的载波频率,占空比低于5%时将出现波形不稳。推测尺度更短的高压脉冲放电在改善三角翼失速特性上更有潜力。不同曲率的前缘处流体动能分布不同,显著影响了脉冲激励的掺混效果,进而影响诱导流向涡的形成和发展,需要进一步的数值模拟研究和精细化的锁相流场显示揭示流动控制机理。