一种基于广义Jaccard系数的改进SAMP压缩信号快速恢复算法
2023-05-06时天昊白银山沈志远
时天昊, 白银山, 沈 堤, 沈志远
(1.南京航空航天大学民航学院,南京,211106;2.94116部队,新疆和田,848000;3.空军工程大学空管领航学院,西安,710051)
根据《“十四五”民用航空发展规划》,预计到2025年,民用运输机场数量达到270个以上,保障起降架次1 700万。民航的快速发展导致机场终端区的频谱资源需求及安全隐患大大增加,对频谱的快速高效监测可以指导频谱的智能管理。在机场终端管制区认知无线电技术可以包括:利用信号能量检测实现信号状态感知及稀疏化处理,将电磁信号转换成二进制信号,并将二进制信号作为测量信号,引入宽带压缩频谱感知模型,利用压缩感知[1](compressed sensing,CS)算法进行信号传递后的重构工作。压缩感知可以在较小的采样频率的情况下对频谱进行高精度监测,同时在广播式自动相关监视(automatic dependent surveillance-broadcast, ADS-B)的来波信号估计、干扰抑制、空管数据处理等方面也有着广泛的应用。
压缩感知算法是一种高效的信号采集及重构算法,该算法在采样频率远低于奈奎斯特频率情况下依然有着优秀的重构精度,大大降低了信号的传输量,在图像重建[2]、远距离通信[3]等领域有广泛的应用前景。对于压缩感知的研究主要集中在测量矩阵构造、信号稀疏表示、重构算法3个方面[4]。重构算法的选择直接影响着信号恢复的精度及速度。重构算法主要有组合类算法、凸优化类算法和贪婪追踪类算法3种[5]。贪婪类算法凭借复杂度低,重构效果好,收敛速度快等特点得到了广泛应用。贪婪算法需要较多的先验信息,然后在每次迭代过程中,不断地将迭代目标像原始信号靠近,并通过设定一个收敛条件来结束算法,从而达到具有较高重构精度的信号。常用的贪婪类算法包括匹配追踪[6]、正交匹配追踪[7]、正则化正交匹配追踪[8]、分段正交匹配追踪[9]、压缩采样匹配追踪[10]、子空间追踪算法[11]。但是上述介绍的算法一般需要先验参数稀疏度K来确定迭代的次数,在实际运用中不具备较高的应用性,为了解决这个问题,文献[12]提出了稀疏度自适应匹配追踪算法(sparsity adaptive matching pursuit,SAMP),该算法在稀疏度未知的情况下依旧具有较高的重构精度。SAMP算法在迭代过程中的原子筛选标准均采用的是内积匹配准则,有时会导致2个相似原子信息的丢失,降低重构精度。SAMP-RB算法[13]在原子筛选阶段采用了正则化回溯的思想,用正则化进行原子的二次筛选,大大提高了重构精度,但是由于增加了二次筛选,其算法运行时间也大大增加。文献[14]提出的DSAMP算法用Dice系数代替了SAMP算法中的内积匹配准则进行原子筛选,Dice系数可以更好地突出残差信号中的重要元素组成部分,更准确的选择符合信号重构的原子,大大提高了重构精度。同时,SAMP算法在运行前需要进行一个固定步长设置,过大的步长设置会导致算法的精度达无法达到理想效果,而过小的步长设置会降低算法的运行效率。文献[15]将变步长的思想引入到算法之中,作者利用Sigmoid函数作为变步长的判断条件,利用大步长逼近,小步长渐进的方法提高了算法的重构精度及运行效率。SAMP-PVRB[16]不仅采用了正则化回溯的思想,还将抛物线函数和变步长思想结合,函数的变化率与算法迭代过程中步长的大小变化呈正相关,取得了良好的效果。在变步长思想中增加初始稀疏度估计有助于大小步长的设置,降低算法的迭代次数,Gao[17]根据定理:稀疏度小于等于测量数的1/4时,信号可以完全准确地重建。将初始稀疏度大小设置为测量数的1/4进行取根号处理,与未设置初始稀疏度情况相比重构效率大大提高。
由于民航终端区频谱资源态势复杂,以上方法在解决频谱感知等问题时的精度及效率还未达到要求,为解决上述问题,本文提出了一种基于SAMP算法改进的算法:JTVS-SAMP(J代表广义Jaccard系数,T代表t-平均相关系数,VS代表变步长思想)。该算法在原子筛选过程中,利用广义Jaccard系数代替了SAMP算法中的内积匹配准则,并引入t-平均相关系数对初始稀疏度进行预测来确定算法迭代的初始步长,同时引入了变步长的思想来优化算法的重构效率和重构精度。
1 压缩感知
1.1 压缩感知的概述
压缩感知的流程如图1所示[18],主要分为3步:信号稀疏表示、信号采样、信号重构。

图1 压缩感知流程图
常用的信号稀疏化处理包括小波变换[19]、曲波变换[20]、离散傅里叶变换[21]等。图1中,Ψ是N×N维稀疏表示阵,x∈RN是长度为N的一维信号,经过稀疏表示阵处理后,信号就具备了稀疏性,数学表达为:
y=ΦΨx=Θx
(1)
式中:y∈RM为压缩信号;Φ表示测量矩阵;Θ=ΦΨ为M×N的感知矩阵。
如果一个信号本来就具备稀疏性且为一维的,那就可以直接使用一个测量矩阵来对信号进行测量,数学表达为:
y=Φx
(2)
式中:Φ∈RM×N,M≪N为测量矩阵;y是被测量矩阵测量后的测量信号。
在信号的采样过程中,会丢弃原始信号x大量的无用信息,因此测量信号会有一定程度上的能量缺失,Tao和Candès证明了稀疏度为K的测量信号要从M个测量值准确的进行信号重构,就要保证测量矩阵Φ满足有限等距特性[22](restricted isometry property,RIP)。
信号重构过程即对式(2)的逆向求解过程。在式中M≪N,因此x的解会有无穷多个,考虑到x具有稀疏性,可以把信号重构过程转换成l0范数问题进行计算[23],信号重构的数学模型可表示为:
(3)
式中:‖·‖0是一个非凸函数,代表输入信号中非零元素数量,对于公式的求解属于NP(non-deterministic polynomial,NP)难问题,无法直接求解,文献[24]将L0范数最小化问题转换成了更加简单的L1范数最小化问题,实现了从非凸向凸的转变,计算式如下:
(4)
1.2 SAMP算法
SAMP算法是贪婪类算法的一种,该算法不需要稀疏度K等先验信息,更符合自然界信号的实际情况。算法步骤流程如下:

表1 SAMP算法步骤
2 JTVS-SAMP算法
2.1 算法改进
2.1.1 基于广义Jaccard系数的原子筛选
传统的SAMP算法采用了内积匹配准则[25]来作为原子筛选标准,原子与迭代过程中的残差匹配度越高,其内积计算结果越大,将该原子加入到支撑集中就可以更快地逼近原始信号,可以达到较为优秀的重构精度,内积匹配准则表达式为:
(5)
式中:x=(x1,x2,…,xn);y=(y1,y2,…,yn)。
由于内积匹配准则更多地考虑了原子和信号残差之间角度的差距,缺乏对信号本身的关注,这会导致在原子筛选过程中会忽略2个相似度较高的原子,造成信号丢失,降低重构质量。为了避免上述情况的出现,引用了广义jaccard系数来代替内积匹配准则[23],计算式如下:
(6)
由式(6)可以看出,广义jaccard系数可以反应出2个向量之间的相似度。分母上放大了2个原子的差异部分,减去了两者的相似部分,使得原子不容易混淆,减少了重要信息的丢失,使得重构精度大大提升。
2.1.2 初始稀疏度的预估计
准确合适的初始稀疏度估计可以指导设置初始步长,有效地减少迭代次数,提高运行效率,本文采用的稀疏估计策略基于如下性质[26]:
当满足RIP条件的测量矩阵Φ在稀疏度K下有以下规定时:
(7)
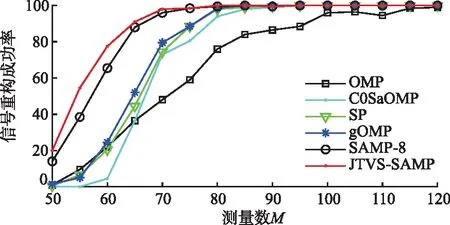
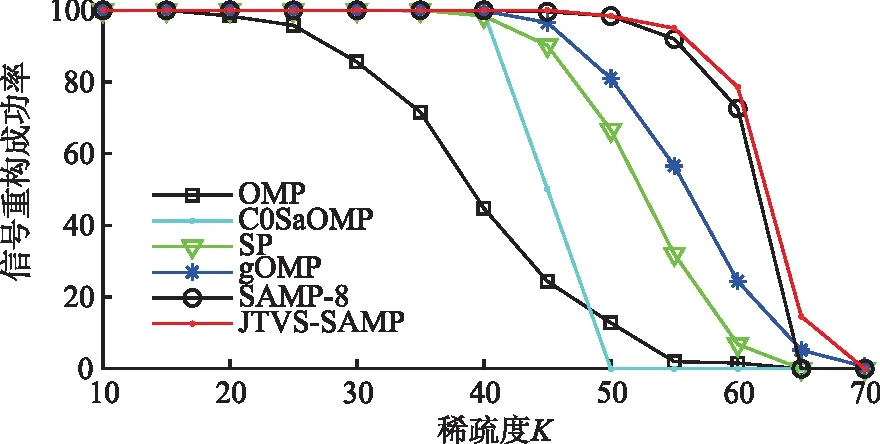
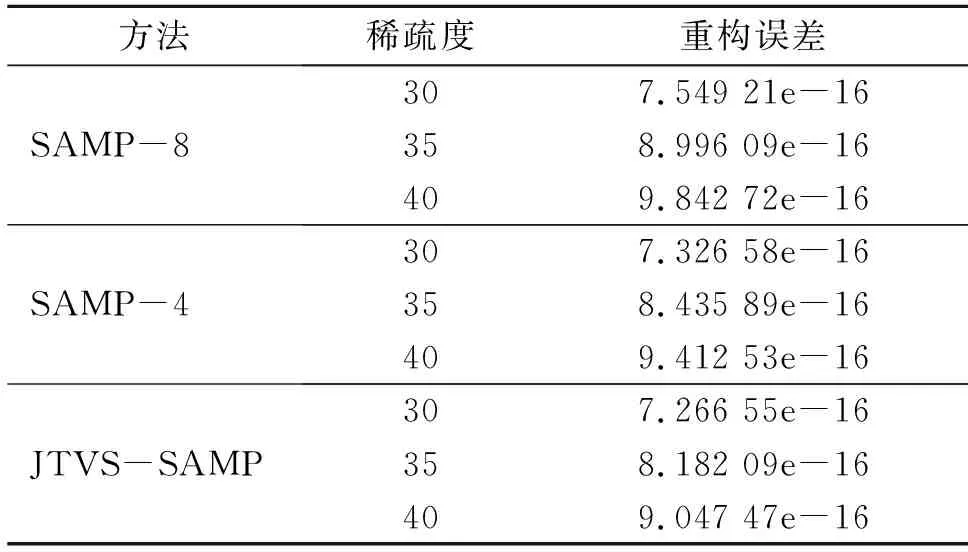
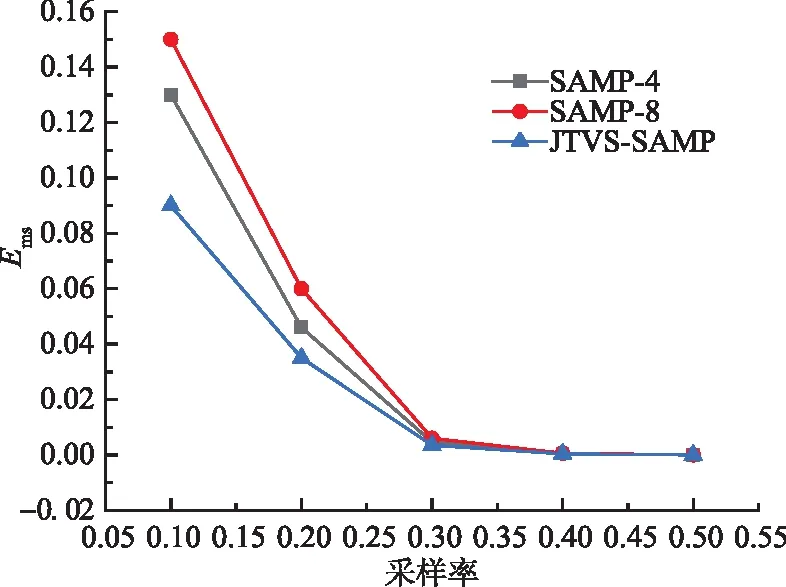
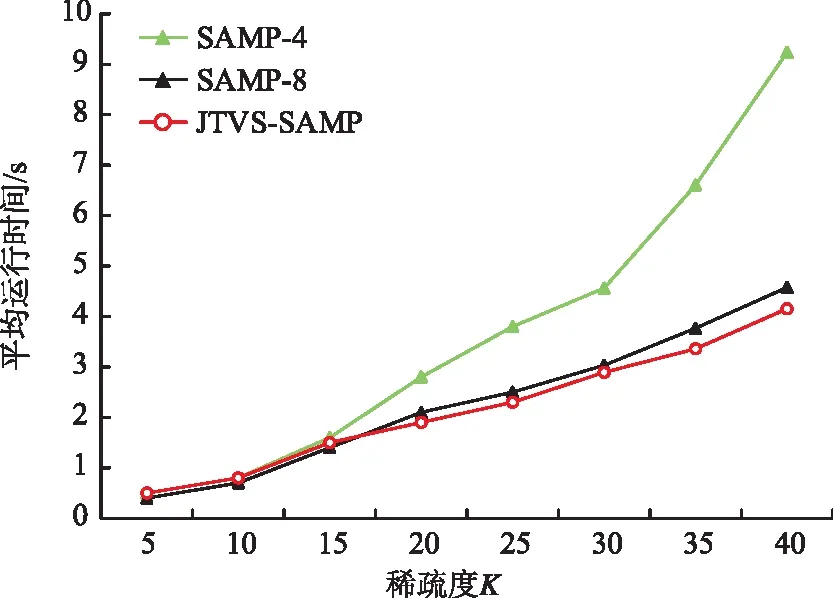
式中:‖Λ‖0=K0,则K0 式(7)中RIP系数δK计算复杂,不容易通过计算得出准确结果。δK与矩阵的正交性呈正相关,其值的大小与信号采样过程中保留的原始信号信息有关,与0越靠近代表保存的原始信息更完整。根据上述特点,引入了t-平均相关系数来代替RIP系数δK,可以在保证稀疏度估计精确度的同时大大降低计算复杂度,如式(8)所示: (8) 式中:μt(Φ)是测量矩阵Φ的t-平均相关系数。 t-平均相关系数作为测量矩阵的评价指标,定义如下[27]: (9) 由此,可以对初始稀疏度K0进行估计,初始化K0=1,代入式(8)进行验证,如果满足条件,则K0=K0+1,继续代入公式验证,否则就结束迭代并输出K0。 2.1.3 迭代过程中的变步长处理 在测量矩阵满足RIP条件的前提下,测量信号y与原始稀疏信号x满足以下关系[17]: (10) 虽然考虑了大小步长变化的方法来平衡重构效率及重构精度之间的平衡,但是由于稀疏度K的未知性,无法准确地确定算法迭代的次数,若在最后一次迭代计算时,步长S仍然有着较大的值,可能会导致过估计[28]的现象,为了避免出现上述情况,结合回溯的思想,本文提出了一种步长S的处理方法。若最后一次迭代过程中,步长S=1,就不进行额外处理;若S>1,则将迭代中的参数回溯至上次迭代的数据,然后以步长S=1继续迭代,直到再一次满足迭代结束条件,经过回溯处理后,重构信号的误差会大大降低。 根据以上改进措施,本文在SAMP算法的基础上提出了JTVS-SAMP算法,步骤流程如下: 表2 JTVS-SAMP算法步骤 为了比较本算法和其他算法重构精度及重构效率上的优越性,本文选择一维高斯随机稀疏信号来模拟算法所需的测量信号,该信号可以有效的模拟机场终端区信号经过能量检测处理后的信道状态[27]。测量矩阵Φ选择为高斯随机矩阵进行信号采样,实验中所采用的对比算法为实验选用OMP、CoSaOMP、SP、gOMP、SAMP,参数设置见表3。 表3 仿真参数表 本文所有实验运行的平台为MATLAB R2022a,计算机配置为Intel i5-6500 CPU @ 3.20Hz,8.00 GB RAM,Windows 7。为避免额外因素干扰,程序运行期间保证后台其余程序全部关闭。 每种算法实验重复500次,运行结果见图2。 图2 不同观测值信号重构成功率 从图中的曲线我们可以看出,随着测量数M的的增加,各个算法的信号重构成功率都有较大的提升。50 图3 不同稀疏度信号重构成功率 从图3可以看出,在测量值为定值的情况下,随着稀疏度K的增加,所有的算法信号重构成功率均呈现不同程度的下降。JTVS-SAMP算法下降速度远远慢于其它算法,在稀疏度K=65的时,依然保持着一定的信号重构成功率,而SAMP算法的重构成功率已经接近0。 为了验证JTVS-SAMP算法及SAMP算法在信号重构成功情况下其重构精度的优劣,我们引入了重构误差这个指标来表示重构信号和原始信号的相似性,重构误差越大,代表信号重构效果越差,计算公式如下: (11) 选择K=30,35,40共3个稀疏度。SAMP算法的步长设置由2~8,选取步长为4和8两种情况进行对比分析。对每个特定K值条件下仿真1 000次,统计仿真结果计算信号的平均重构误差,见表4。 表4 重构误差对比表 由表格可得,随着稀疏的K的增加,JTVS-SAMP、SAMP-4和SAMP-8的重构误差都会逐渐增大,SAMP-4相比于SAMP-8,采用了更小的步长设置,在算法迭代过程中具有更高的精度,因此其重构误差小于SAMP-8的重构误差。JTVS-SAMP的重构误差略优于SAMP-4算法,这是因为JTVS-SAMP算法利用广义Jaccard系数筛选原子、小步长逼近等措施,使得该算法具有较高的精度。 信号采样率的大小是测量数与信号长度的比值,代表了采集过程中的所需的信号采集数量。为了证明算法在不同信号采样率情况下的重构性能,引入均方误差(MSE)作为评价指标,其计算公式如下: (12) 在压缩感知中,测量信号K≤M/4是稀疏信号完全恢复的充分条件[17]。因此在本次仿真实验中,设置测量信号稀疏度K=M/4。采用SAMP算法作为对比算法,其步长设置分为4和8两种情况,探讨采样率为0.1,0.2,0.3,0.4,0.5情况下的改进算法与对比算法的重构精度,结果见图4。 图4 不同采样率下的算法均方误差比较图 从图4可以看出,随着采样率的增加,3种算法的均方误差数值在逐渐减小,当采样率大于0.3时,所有的算法均可以完成高精度信号重构,但在低采样率的信号重构过程中,JTVS-SAMP算法相比于SAMP算法,具有更高的误差控制能力,表明了算法在低采样率情况下也具有较高的算法稳定性。 为了验证JTVS-SAMP算法的重构效率的优越性,使用Matlab软件进行算法用时统计,与步长设置为4、8的SAMP-4、SAMP-8算法进行比较。采样信号固定测量数M=128,设置稀疏度K从5开始,步长为10增加到40。进行循环200次处理计算平均运行时间,仿真结果见图5。 图5 平均运行时间对比图 由图5可以看出,随着稀疏的K的增加,3种算法的平均运行时间都在增加,这是由于信号重构的内容增多,其耗费的时间也在逐渐增加。SAMP-4的平均运行时间大于其余两种算法,是由于其步长设置较小导致的效率偏低。JTVS-SAMP算法在效率方面略优于SAMP-4算法,这是因为JTVS-SAMP算法对初始稀疏度进行了预测,且采用了变步长的思想,在大步长阶段的快速迭代,大大降低了算法所需时间。 本文基于的SAMP算法,通过融合广义Jaccard系数、t-平均相关系数、变步长思想,提出了JTVS-SAMP算法。相比于SAMP,COSaOMP,gOMP等传统压缩感知算法,在使用二进制信号模拟信号能量检测后的机场电磁信号时,JTVS-SAMP算法在同稀疏度不同观测值、不同稀疏度同观测值下的情况下,算法重构的成功率表现更为优秀,且与其原算法SAMP相比,在重构误差、低采样率信号稳定性、重构时间等方面均有了明显的提高。该改进算法未来可在机场终端区频谱分析、波达方向估计等领域广泛应用。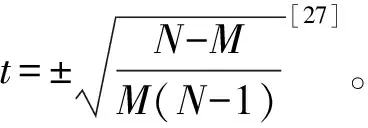
2.2 算法步骤

3 仿真结果及对比分析

3.1 不同观测值下的算法重构成功率
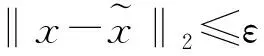

3.2 不同稀疏度下的算法重构成功率
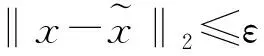
3.3 不同算法的重构误差比较
3.4 不同信号采样率情况下的重构精度分析
3.5 算法重构时间的比较
4 结语
