基于双模式更新五行环算法的多目标冷链配送

任 静，项 月，刘漫丹

（华东理工大学信息科学与工程学院, 上海200237）

冷链物流作为物流业的一个重要分支受到了越来越多的关注。我国在冷链物流配送的过程中，冷链产品的损失金额约为1 亿人民币，足以满足2 亿人口的基本需求[1]。近年来，针对冷链物流配送中的路径规划问题，不论是在模型建立还是在算法求解方面都取得了大量的研究成果。

在模型建立方面，Wang 等[2]建立了以配送成本最低为目标函数的模型；Govindan 等[3]建立了以配送成本最小化、环境影响最小化为目标函数的模型；Caoa等[4]建立了以车辆数最小化、计划距离最小化等为目标函数的模型；Wang 等[5]建立了以交货成本最小化、生鲜产品新鲜度最大化为目标函数的模型。

在求解算法方面，Gong 等[6]提出了一种改进的粒子群优化算法来解决带时间窗的路径规划问题；Wang 等[7]提出了一种基于时空的邻域搜索-遗传算法的两阶段启发式算法来解决多目标路径问题；Zhao 等[8]提出了一种改进的蚁群算法来求解冷链物流中的路径规划问题；Claudia 等[9]采用两阶段法求解柔性周期车辆路径问题；Chen 等[10]提出了一种自适应的大型邻里搜索算法来解决具有时间窗的车辆路径规划问题。

五行环优化(FECO)算法[11]是近年来提出的一种新型的优化算法，因其采用元素空间结构，在全局探索和局部探测方面可实现较好的平衡性。相比于经典的优化算法以及一些其他的新型算法，FECO 算法在解决单目标路径优化问题中取得了很好的优化结果。基于FECO 算法，本文提出了一种双模式更新个体的五行环优化算法(Five-Elements Cycle Optimization Algorithm of Dual-Mode Updating Individuals, FECODMUI)用于求解多目标优化模型，并与FECO 算法、NSGA-II 算法[12]、鲸鱼优化算法(Whale Optimization Algorithm, WOA)[13]、灰狼优化算法(Grey Wolf Optimizer，GWO)[14]进行比较，通过具体实例验证了FECO-DMUI 算法能够为冷链物流配送提供可实施的有效方案。

1 相关背景

1.1 问题描述

根据顾客对配送时间的满意度可以将顾客分为两类[15]，每类顾客的满意度情况如图1 所示，本文的优化模型依据普遍存在的第二类顾客而建立。冷链物流配送问题可描述为：某区域设有一个冷链产品的配送中心，该中心含有G辆车负责向N个客户点配送，每辆车的起点与终点均为配送中心。根据图1分析得：①为最优配送时间范围；②为可接受配送时间范围；③为拒绝配送时间范围。

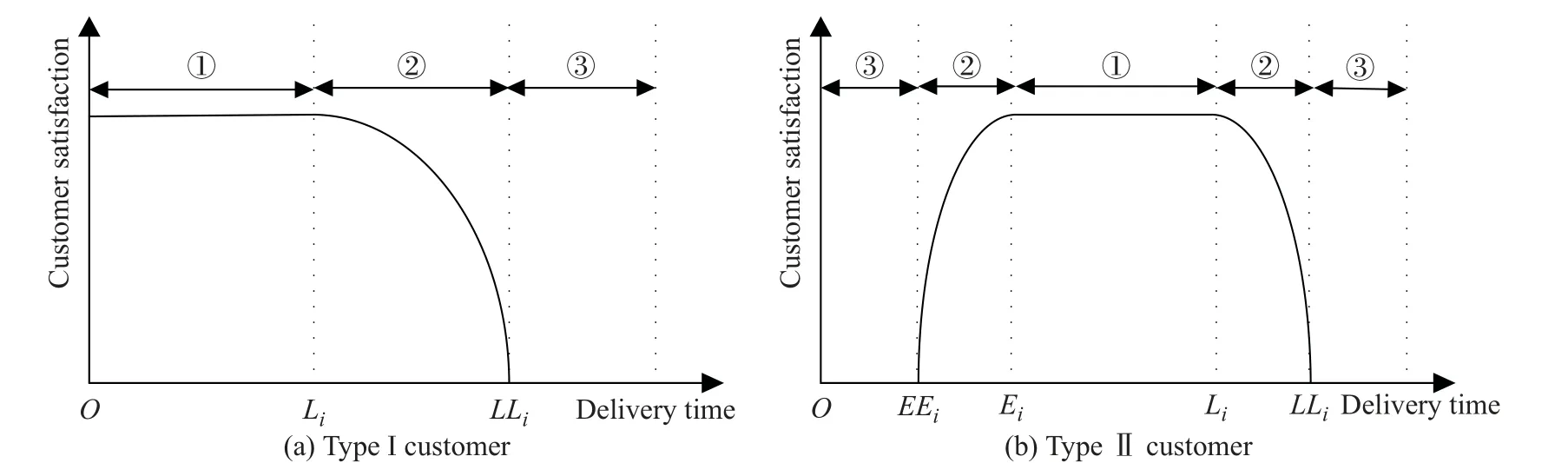
图1 顾客满意度分析Fig.1 Customer satisfaction analysis

1.2 问题假设

假设 1：每辆车的最大载重量已知，并且客户的需求量不会超过车辆的最大载重量。

假设 2：每个客户点之间的距离均预先可知且每个客户点只用一辆车进行配送。

假设 3：每辆车的起点与终点均为配送中心且车辆在整个运输过程中以近似恒定的速度行驶。

假设4：每个客户点均有时间窗限制，如果没有按照规定时间送达则产生相应的惩罚成本。

2 模型的建立

2.1 参数及变量设定

模型参数的设定：Q为车辆的最大载重量；h为单位里程的运输成本；e为燃料单价；µ1为运输中单位时间内制冷设备的能耗；µ2为装卸过程中单位时间内制冷设备的能耗；s为运输过程中车辆行驶的恒定速度；p为冷链货物单价；c1为提前服务引起的惩罚成本；c2为延迟服务引起的惩罚成本；α 为装卸过程中的货损率；β 为货物对时间的敏感系数；[Ei,Li]为客户i的最优时间窗；[EEi,Ei,Li,LLi] 为客户i的特定时间窗；di j为客户点i与客户点j之间的距离，i或j为0 时，代表配送中心，否则代表各客户点；qi为客户点i的需求量。

模型变量的设定：tiv为车辆v到达客户点i的时间；wi jv为车辆v到达配送点的时间，当车辆v由配送点i行驶到配送点j时，wijv=1 ，否则为0（wiiv=0 ，i或j为0 时，代表配送中心，否则代表各客户点）；yiv表示客户点i是否由车辆v配送，是，yiv=1 ，否则为0。

2.2 配送成本模型

配送成本f1由运输成本C1、货损成本C2、制冷成本C3和时间惩罚成本C4构成。

2.2.1运输成本 冷藏车辆产生的运输成本主要包含燃料成本以及车辆的维修成本，具体表达形式如下：

其中：N为配送点的数目；G为配送车辆的数目。

2.2.2货损成本 相对于传统物流，冷链物流的关键是保证冷链产品的新鲜。在实际情况中，配送车辆长时间行驶使得冷链产品腐烂变质或品质下降；在装卸货物过程中，冷链产品与外部热空气接触，温度升高会使冷链产品的质量遭到损坏[16]。本文的货损成本模型根据文献[17]改进所得，具体表达形式如下：

2.2.3 制冷成本 由于车辆在运输过程中维持冷链产品的低温和到达客户点进行交货过程中产生的能耗成本[18]均不可忽视，因此本文的制冷成本模型根据文献[18]改进所得，具体表达形式如下：

2.2.4 时间惩罚成本 不论配送车辆到达的时间早于Ei还是晚于Li，均会增加配送成本。因此，只要车辆在客户规定的最优时间窗外到达，就要产生相应的惩罚成本。具体表达形式如式（4）所示。

2.3 客户满意度模型

客户满意度f2的评估是基于配送车辆到达客户点的时间建立的。根据图1 建立的评估函数如式（5）所示：

在该评估函数中，当tiv位于 [Ei,Li] 时，客户的满意程度为1；当tiv位于 [EEi,Ei] 或 [Li,LLi] 时，满意程度位于 (0,1) ；当tiv位于 (0,EEi] 或 [LLi,∞) 时，满意程度为0。因此，最终建立的客户满意度模型如式（6）所示。

2.4 冷链物流模型

本文建立的是单个配送中心和多个客户点的模型，优化目标为最小化配送成本f1、最大化客户满意度f2。目标函数和约束条件的表达式如下：

其中，目标函数式（7）表示配送成本最小化；式（8）表示客户满意度最大化；约束条件式（9）表示保证每个客户点都能接受服务；式（10）、式（11）、式（12）表示每个客户点只用一辆车服务；式（13）表示客户需求量不超过车辆的最大装载量；式（14）表示保证每一辆车的起点和终点都是配送中心。

3 FECO-DMUI 算法的求解

3.1 FECO 算法的原理

Liu[19]提出的FECO 算法利用了五行元素(金、木、水、火、土)相生相克的关系（图2），将金、水、木、火、土这5 个元素分别用序号1、2、3、4、5 来表示。假设在k时刻，各元素的质量为mi(k) ，各元素受到其他4 个元素所施加的合力为Fi(k) ，其中i=1,2,3,4,5。由F于i(k)是由4 个元素施加的力组成，并且每个元素施加的力所产生的作用并非完全相同，定义、wgp、wrp、wgawra分别为上述4 个元素施加的力的权重系数，因此所建立的五行环模型(Five-ElementsCycleModel,FECM)[12]如下：

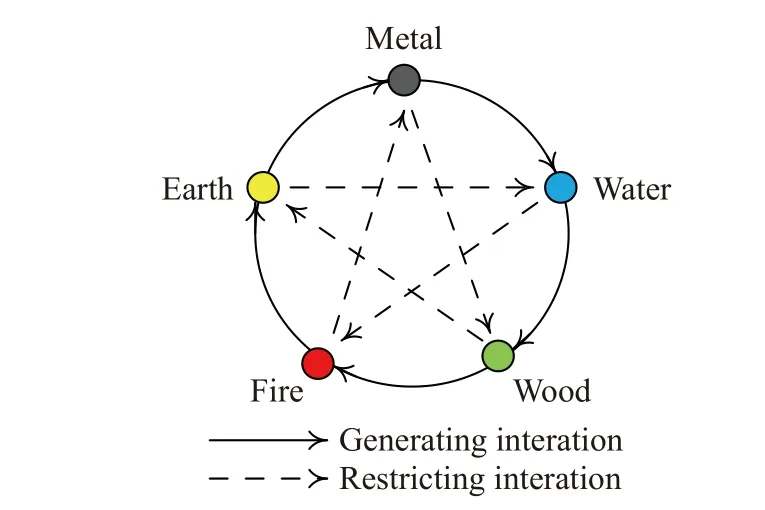
图2 五行元素相生相克关系Fig.2 Five elements complement each other

在求解优化问题时，往往将FECM 中的五行元素拓展为任意元素，并将所有元素划分为q个环，每个环包含L个元素。xij(k) 表示第k时刻第j个环中的第i个元素，mi j(k) 表示元素xij(k) 的质量，Fij(k)表示元素xij(k) 所受第j个环中的其他元素的作用合力，Fi j(k) 的表达形式如下：

在FECO 算法中，Fi j(k) 的大小反映了元素xij(k)质量的优劣。当Fi j(k)>0 时，元素xij(k) 的质量较优。因为在系统平衡中大的受力会使元素变得强壮，所以当前的xij(k) 被保留到下一代。当Fi j(k)<0时，元素xij(k) 的质量较差。Fi j(k) 为负，说明系统期望当前元素变得更加衰弱，所以当前的xij(k)会被其他元素替换。重复此过程，直至达到最大迭代次数，即可获得所求问题的最优解。

3.2 FECO-DMUI 算法的适应度函数以及个体的编码与解码

本文模型中初始化种群n=L×q，选取式（7）和式（8）作为评估函数。由于需要将客户点与配送车辆同时进行编码，所以采用随机键[20]的方式。若客户点数为N，配送车辆数为G，则个体xij(k) 的编码长度为N+G−1 ，每一位的取值范围是 [0,1] 之间的小数。由N+G−1 个 [0,1] 之间的小数组成一个个体xij(k)的过程即为编码。解码时，首先对个xij(体k)中的每一位进行大小排序，最小值对应1，次小值对应2，以此类推，通过这样的方式将个N+G−1[0,1]之间的小数转化为1～N+G−1的自然数排列。其中1～N表示客户N+点1N，+G～ −1表示线路分割符号，通过线路分割符号得到每辆车的配送路线。以图3 为例，客户点数N=10 ，车辆数G=3 ，则个体的长度为12，1～10 表示客户点，11～12 表示线路分割符，因此每辆车的配送路线为：第1 辆车：1→5；第2 辆车：8→3→2；第3 辆车：10→7→4→6→9。

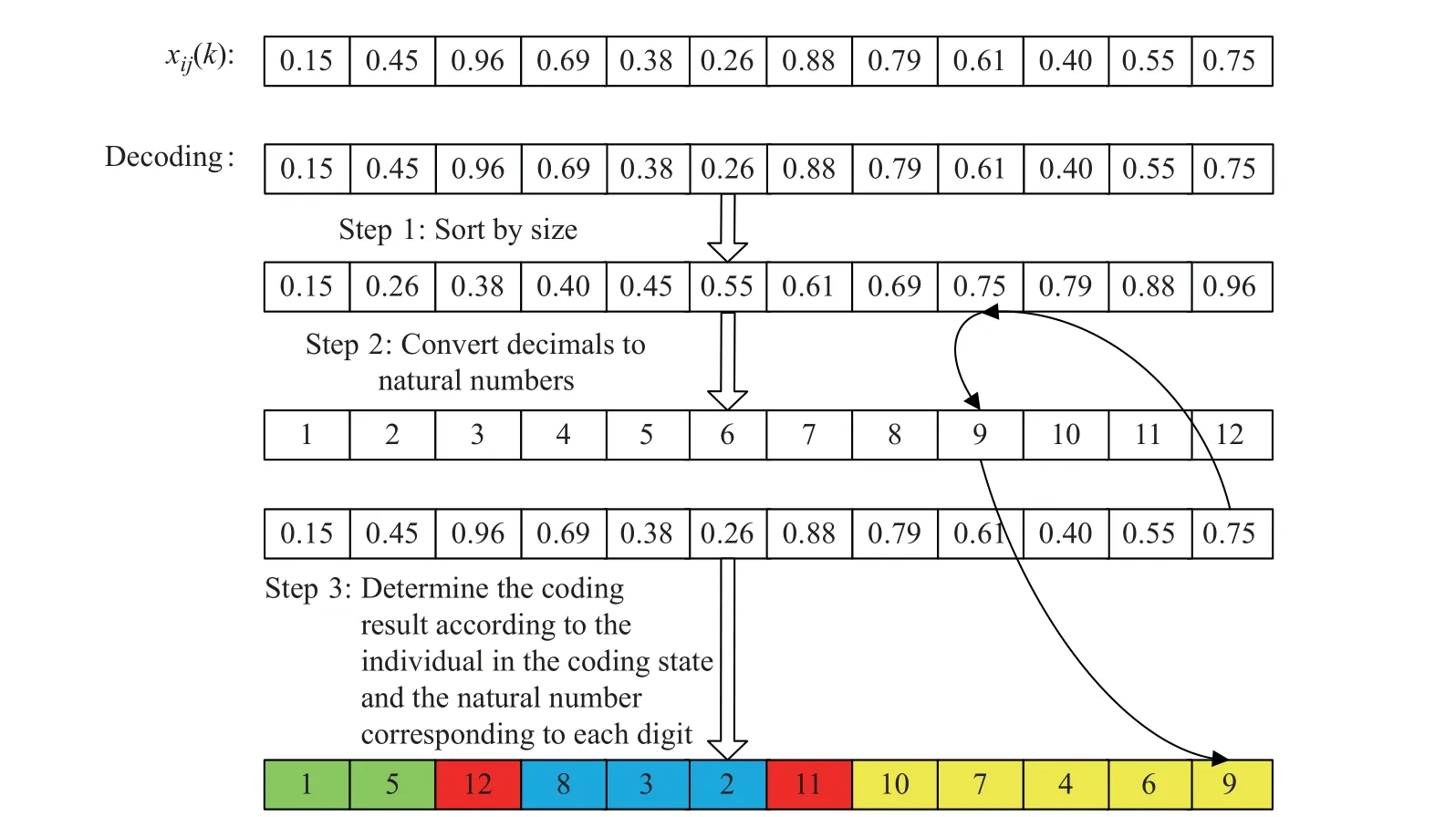
图3 编码与解码操作Fig.3 Encoding and decoding operations

3.3 FECO-DMUI 算法通过选择、交叉和变异产生新个体

3.3.1 选择 本文采用的选择方式为锦标赛选择[21]。每次从种群规模为n的种群中抽取n/2 的个体，从已抽取的个体中选择目标函数达到最优的一个进入子代种群。重复上述操作，直到新的种群规模达到原来的种群规模n。对于多目标优化模型来说，目标函数最优是指从当前Pareto 前沿面上的两个端点解以及拥挤距离最大的解中随机选择一个，这样既能迭代出最优解也能找到更均匀的Pareto 前沿面。

3.3.2 交叉 本文采用的交叉方式为单点交叉，交叉概率为pc，即在当前迭代过程中的个体xij(k) 中随机产生一个交叉点，以该交叉点为基准相互交换两个个体、的序列，产生新的个体、，统。交叉过程如图4 所示。

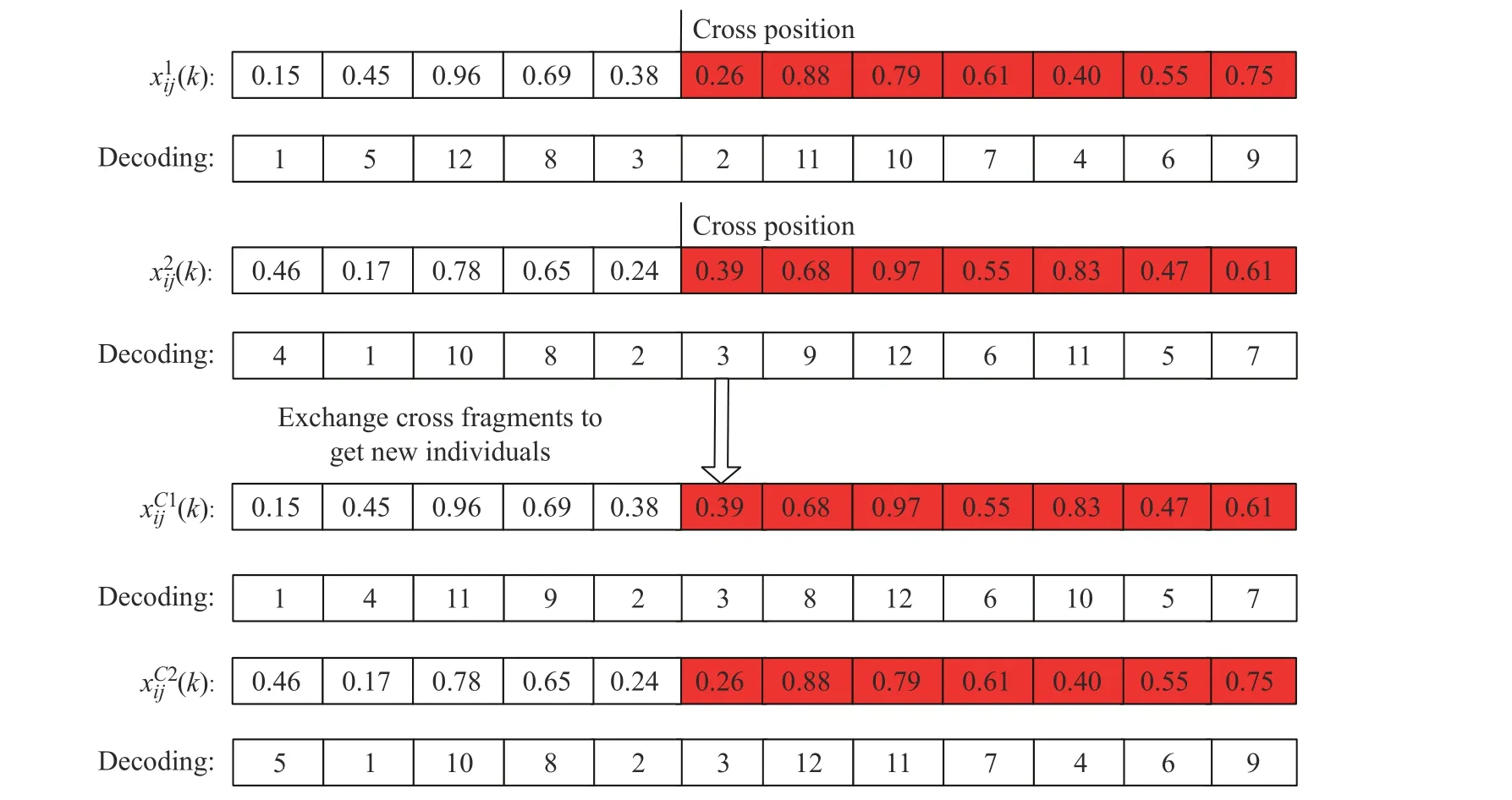
图4 交叉操作Fig.4 Cross operation

3.3.3变异 本文采用的变异方式为单点变异与高斯变异各占一半的混合变异方式，即每个个体以0.5 的概率选择单点变异或高斯变异，变异概率为pm。采用单点变异时，随机产生一个变异点，用新生成的[0,1]之间的小数替换初始变异点上的数。采用高斯变异时，随机产生一个变异点，用一个均值为µ、方差为 σ2的正态分布的随机数替换初始变异点上的数。通过变异产生的新个体记为。变异过程如图5 所示。

图5 变异操作Fig.5 Mutation operation

3.4 FECO-DMUI 算法通过对受力大小的判断产生新个体

本文中，个体xij(k)代表冷链物流优化模型的一个解，f1(xij(k))、f2(xij(k))为其目标函数的值，mi j(k)表示元xi素j(k)的质量。由于本文建立的模型为多目标优化模型，所以将个体xij(k)的非支配等级赋值给。mi j(k)是Fi衡j(k)量个体xij(k)质量优劣的变量，因此，通过对受力大小的判断来产生新个体的方式就是根据的Fi j(值k)来更新个xi体j(k)，得到的新个体记为。根据式（17）计算Fi j(k) 的值。若Fi j(k)>0 ，说明当前个体xij(k) 的质量较优，则保留当前个体，即=xi j(k)。若Fi j(k)≤0 ，说明当前个体xij(k) 的质量较差，则根据式（18）更新当前个体。

式中：rs、rm分别取 [0,1] 区间的随机数；ps表示尺度因子；pn表示给定的概率；xrank1∗(k) 表示在Pareto 排序为1 的个体中随机选取的某个个体；xbest(k)表示种群中的全局最优个体。

3.5 个体的修复

在更新过程中还需要判断更新后的个体是否存在线路分割符相邻或处于首末位的情况。若存在，就会有车辆闲置，此时修复的方法为：将包含客户点最多的配送路线中的第1 个客户点分配给闲置的车辆。以图4 为例，此时的个体出现了车辆闲置的情况，修复结果如图6 所示。修复前的路线为：第1 辆车：5→1→10→8→2→3，第2 辆车：7→4→6→9，第3 辆车闲置；修复后的路线为：第1 辆车：1→10→8→2→3，第2 辆车：7→4→6→9，第3 辆车：5。

图6 个体的修复Fig.6 Individual repair

3.6 非支配排序与拥挤度计算

对于多目标优化问题而言，非支配排序和拥挤度计算是求取Pareto 最优解集的关键。在FECODMUI 算法中，经过选择、交叉和变异产生的新个体为，形成的种群规模为n；通过对受力大小的判断产生的新个体为，形成的种群规模也为n。将两种方式产生的新个体合并后，通过非支配排序与拥挤度计算筛选出n个个体形成新的种群，并使其进入下一次迭代。

3.7 FECO-DMUI 算法流程

FECO-DMUI 算法流程如图7 所示。首先，初始化种群xij(0)，mi j(0) 和Fi j(0) ；其次，对初始化种群进行非支配排序与拥挤度计算，并将每个个体的非支配等级赋值给mi j(k) ；然后，在每一次的迭代过程中，通过两种方式产生新的个体；最后，将两种方式产生的个体合并形成规模为 2n的种群，重新计算合并后种群的非支配排序与拥挤度，通过每个个体的非支配等级与拥挤度选出新的较优个体组成新的规模为n的种群，进入下一次迭代。当迭代次数达到最大时，算法结束并得到最终的Pareto 最优解集。

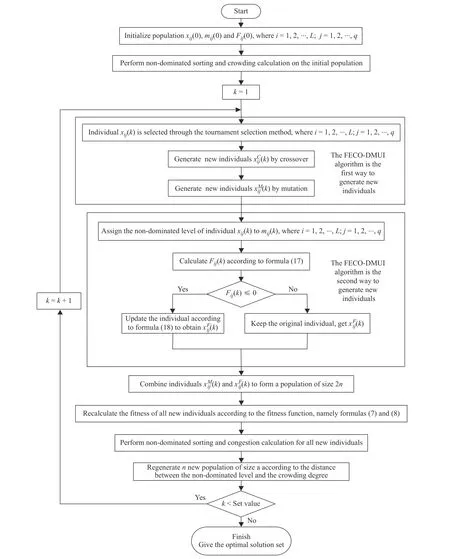
图7 FECO-DMUI 算法流程图Fig.7 Algorithm flowchart of FECO-DMUI

4 算例分析

4.1 相关数据

为了验证本文模型与算法的有效性，借鉴了文献[22]中客户点和配送中心的相关数据来实现本文模型。客户点信息如表1 所示，其中0 代表配送中心，1～25 代表客户点。为了更清晰地了解配送中心与客户点的位置，图8 示出了具体的分布图，横、纵坐标分别代表客户点与配送中心在平面图中的x轴与y轴。

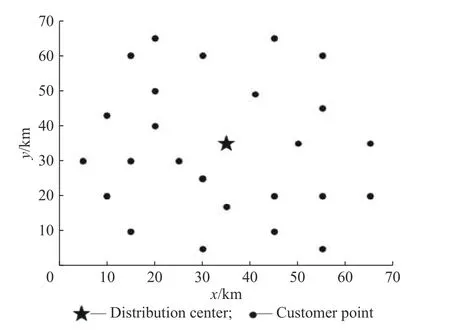
图8 客户点分布图Fig.8 Distribution map of customer point

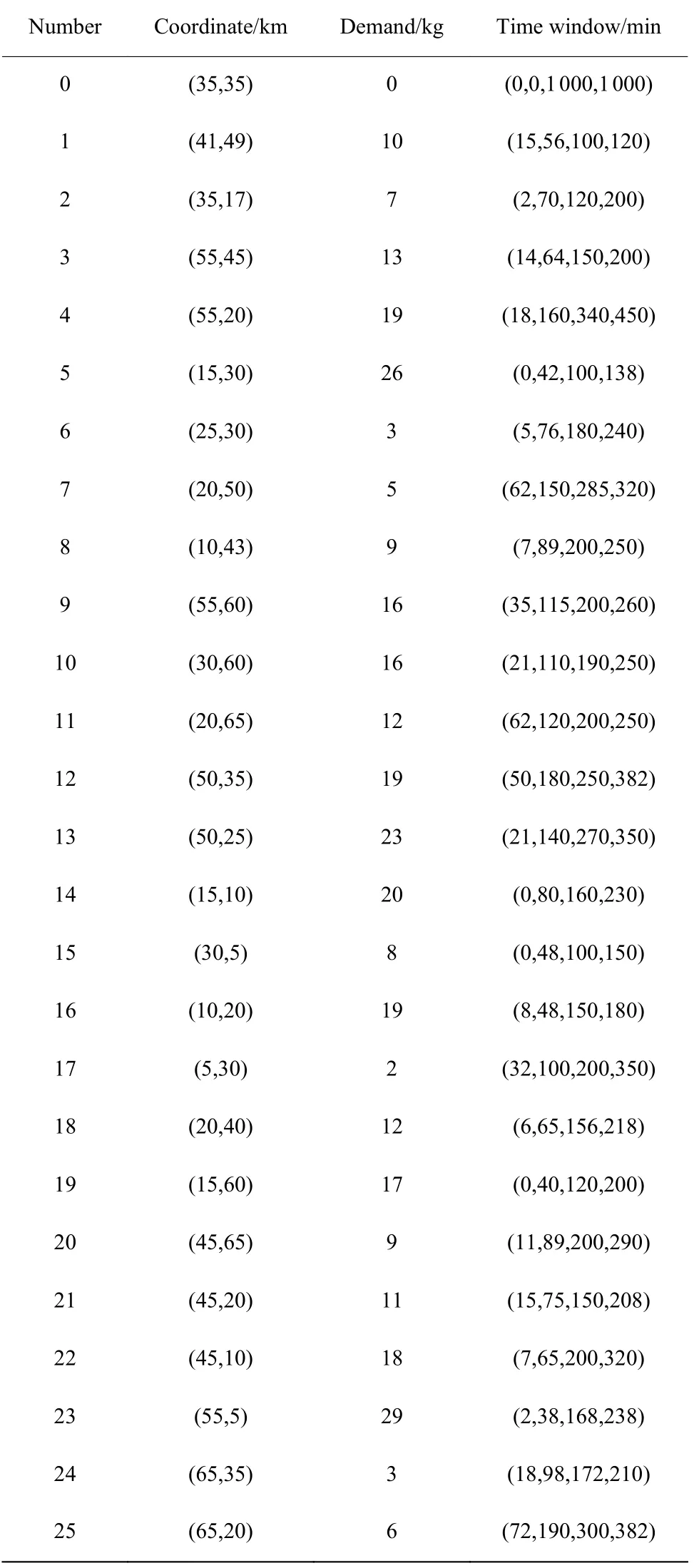
表1 客户点信息Table 1 Customer point information

算例设置如下：1 个配送中心，由4 辆车向25 个客户点进行配送。优化模型中涉及的参数取值如表2所示。实验平台为MATLAB R2019b 版本。

表2 优化模型参数取值Table 2 Parameter values of optimize model

4.2 算法参数分析

经过反复测试得出，当最大迭代次数 (kmax) 为2 000、环的个数 (q) 为40 以及每个环中包含的元素个数(L)为5 时，FECO-DMU 算法处于收敛状态且算法性能最优。当权重系数取值为1 时，算法性能达到最佳[11]。对于其他参数，通过对FECO-DMUI 算法进行多组比较实验来选取合适的取值。选取的一组基本参数值为：交叉概率（pc）为0.4，变异概率（pm）为0.2，尺度因子（ps）为1，给定的概率（pn）为0.9，当对一个参数进行比较时, 其他参数均选取上述基本值。表3～表6分别给出了每个参数的实验比较结果，均为算法运行10 次所取得的平均值。

超体积指标(Hyper Volume，HV)[23]是评价多目标优化算法综合性能的指标，HV 值越大，说明算法的综合性能越好。在计算HV 时，选取的参考点由顾客满意度和配送成本组成，针对本文提出的多目标优化模型，参考点的具体取值为(58 810，0.5895)，不同的多目标优化模型需根据实际情况选取参考点。

由表3 可知，当pc=0.4 时，HV 值最大，说明此时FECO-DMUI 算法的综合性能最佳。由表4 可知，当pm=0.2 时，HV 值最大，说明此时FECO-DMUI 算法的综合性能最佳。由表5 可知，当ps=1.0 时，HV 值最大，说明此时FECO-DMUI 算法的综合性能最佳。由表6 可知，当pn=0.9 时，HV 值最大，说明此时FECO-DMUI 算法的综合性能最佳。

表3 交叉概率比较实验Table 3 Crossover probability comparison experiment

表4 变异概率比较实验Table 4 Mutation probability comparison experiment

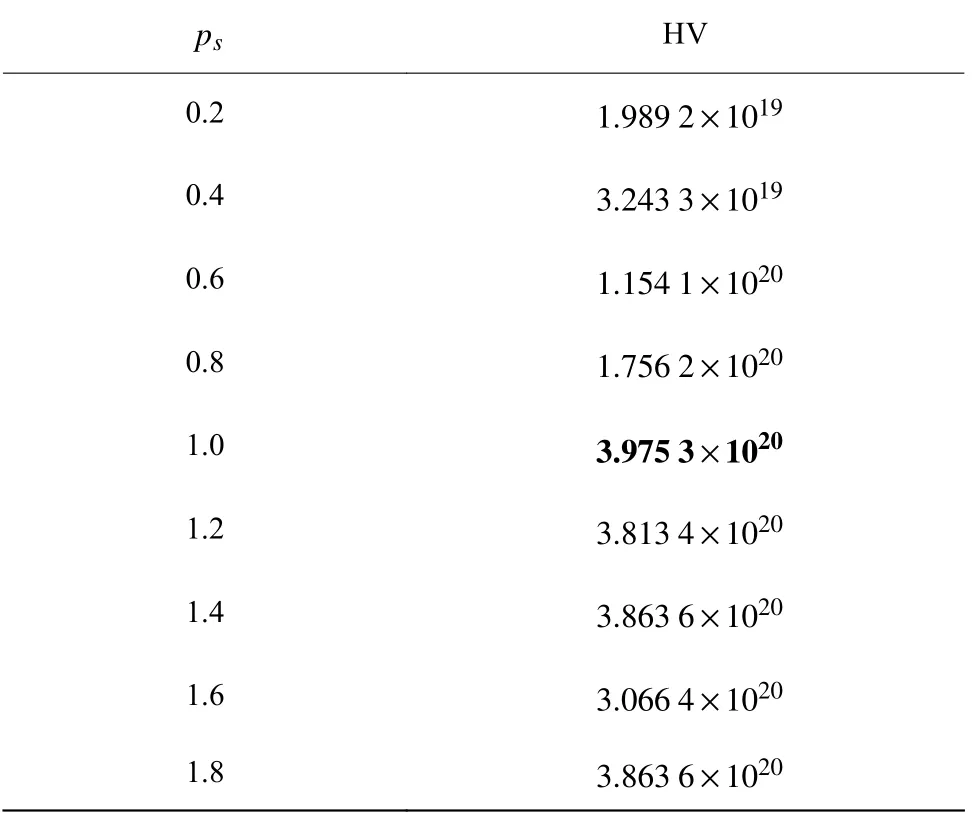
表5 尺度因子比较实验Table 5 Scale factor comparison experiment

表6 给定概率比较实验Table 6 Comparison experiment with given probability

4.3 算法结果分析

利用FECO- DMUI 算法解决多目标冷链物流配送路径优化问题，得到每辆车的配送路径如图9 所示，其中：橙色代表车辆1，紫色代表车辆2，绿色代表车辆3，蓝色代表车辆4。

图9 中的方案分别对应Pareto 解集中的两个端点解以及相对居中的一个解。方案1 为配送成本最小化，此时配送成本为39 861 元，顾客满意度为0.645 4；方案2 为顾客满意度最大化，此时配送成本为57 149元，顾客满意度为0.944 6；方案3 为配送成本与顾客满意度均取折中，此时配送成本为47 646 元，顾客满意度为0.871 9。

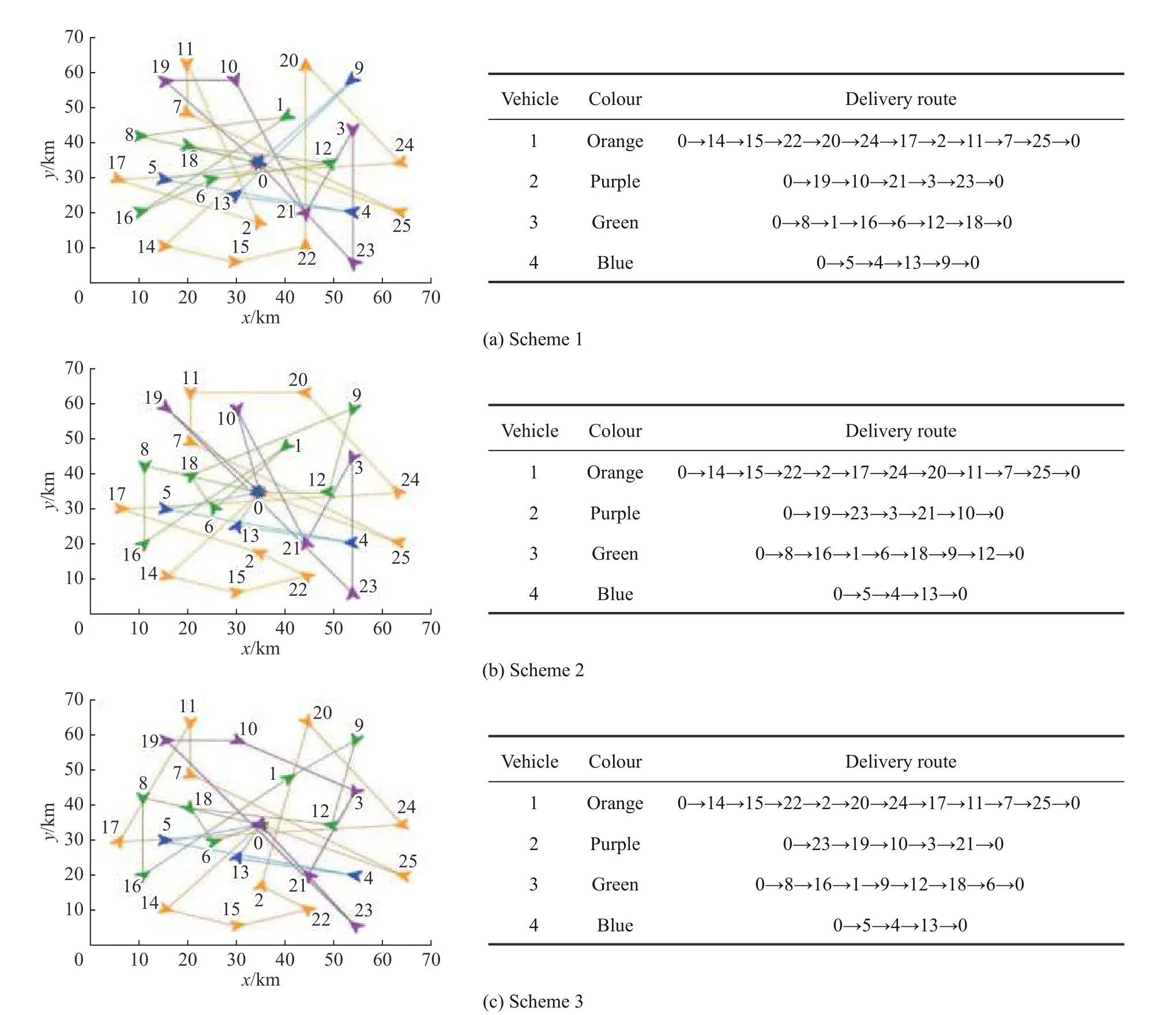
图9 路径规划图Fig.9 Path planning diagrams

本文优化方案比单纯的多回路运输问题(Vehicle Routing Problem, VRP)复杂，原因如下：对于方案3 中的第1 辆车，它经过客户点2 后，直接到达了客户点20，若按最短路径的原则行驶，经过客户点2 后要先到达同一路线上的客户点25，之所以以这样的方式行驶，是因为客户点20 的时间窗为(11,89,200,290)，客户点25 的时间窗为(72,190,300,382)，先去客户点25 很有可能错过客户点20 的最优时间窗，甚至错过配送的整个时间窗，所以选择先到达客户点20，其他类似的情况同理。

4.4 算法对比分析

为了进一步验证本文算法的有效性，基于相同的数据集和编码方式，采用NSGA-II 算法、FECO 算法、WOA 算法以及GWO 算法分别对模型求解，将得到的结果与FECO-DMUI 算法进行对比，进一步验证本文算法的有效性。

FECO-DMUI 算法采用的算法参数和最大迭代次数与4.2 节、4.3 节相同。NSGA-II 算法的n=200，kmax=4 000，p且c=交0.叉4方式均为单点交叉，pm=0.2且变异方式均为混合变异，选择方式依然为锦标赛选择。FECO 算法的n=200 ，kmax=4 000，ps=1 ，pn=0.9以及权wgp=重wrp=系wga=w数ra=1。WOA算法的，n=2，00k系max=数4 000 和r1r2为[0,1]之间的随机数，系数l为[−1,1]内的随机数，定义螺线的形状系数b=1。GWO 算法的n=200 ，kmax=4 000 ，r1，r2的取值与WOA 算法取值相同。

将5 种算法分别对优化模型进行求解，得到Pareto 最优解集分布如图10 所示，对比结果如表7所示。

从图10 可以看出，FECO-DMUI 算法求解所得的Pareto 最优解集明显优于其他算法，同时，FECODMUI 算法得到的可行解的数量多于其他算法。

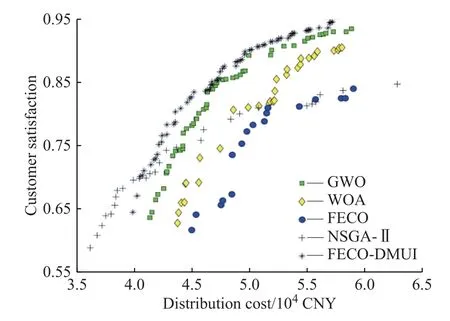
图10 最优解集分布图Fig.10 Optimal solution set distribution graph

表7 中HV 是算法运行10 次所取的平均值。可以看出FECO-DMUI 算法所得HV 明显大于其他算法，证明了算法的综合性能好。选取10 次运行结果中HV 居中的一次，将该次运行结果中各算法获得的Pareto 最优解集中的边界解作为表7 中的“最小配送成本”和“最大顾客满意度”两列。此时，FECODMUI 算法在配送成本的求解上虽不是最优的，但与最优解相差不大，而在顾客满意度的求解上，结果明显优于其他算法。表7 中“平均最小配送成本”与“平均最大顾客满意度”是算法运行10 次取所有最小配送成本和最大顾客满意度的平均值。通过5 种算法的对比可以看出，FECO-DMUI 算法不论是在配送成本的求解上还是在顾客满意度的求解上均最优，充分证明了FECO-DMUI 算法的有效性。

表7 5 种算法的对比结果Table 7 Comparison results of five algorithms

5 结 论

本文基于冷链物流的实际情况建立了以配送成本最小化、顾客满意度最大化为优化函数的多目标数学模型，其中配送成本包含运输成本、货损成本、制冷成本以及时间惩罚成本。在考虑配送成本的同时，通过顾客的特定时间窗和配送车辆到达客户点的时间点来反映顾客满意度，从而达到成本最小化和顾客满意度最大化的优化效果。实例验证表明，FECO-DMUI 算法在求解冷链物流配送的问题中能够得到更优的配送方案，证明了FECO-DMUI 算法的有效性与实用性。