中考中三角形的广泛性探析

文／李蕴欣

通过归纳三角形有关知识的考查方式，我们发现其既能直接求解，也能承接知识点，还能为问题的解决提供关键一环。三角形的广泛性在于，它可以与四边形、圆、平面直角坐标系等为背景的综合题相融合。因此，我们只有会用、用好三角形知识，才能为解决复杂问题提供帮助。

一、三角形与三角形

例1（2022·湖北黄石）如图1，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°，且点D在线段BC上，连接CE。

（1）求证：△ABD≌△ACE；

（2）若∠EAC=60°，求∠CED的度数。

图1

（1）证明：∵∠BAC=∠DAE=90°，

∴∠BAC-∠CAD=∠DAE-∠CAD，

即∠BAD=∠CAE。

在△ABD和△ACE中，

（2）解：∵△ABD≌△ACE，

∴∠ACE=∠ABD。

∵△ABC和△ADE都是等腰直角三角形，

∴∠ACE=∠ABD=∠AED=45°。

∴∠CED=∠AEC-∠AED=75°-45°=30°。

【点评】本题主要考查全等三角形的判定与性质、等腰直角三角形的性质、三角形的内角和定理，掌握全等三角形的判定定理是解题的关键。

二、三角形与四边形

例2（2021·江苏南京）如图2，将▱ABCD绕点A逆时针旋转到▱AB′C′D′的位置，使点B′落在BC上，B′C′与CD交于点E。若AB=3，BC=4，BB′=1，则CE的长为_______。

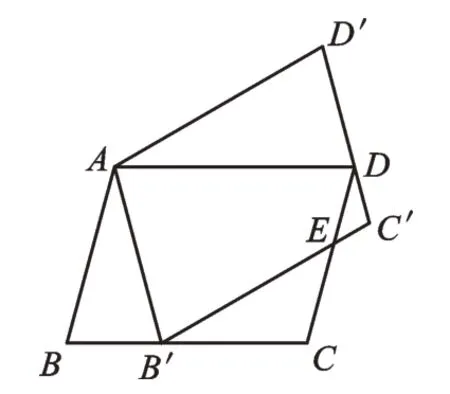
图2

解：如图2，连接DD′。

由旋转可知，∠BAB′=∠DAD′，

AB′=AB=3，AD′=AD=4，

∴△BAB′∽△DAD′。

∴AB∶BB′=AD∶DD′=3∶1。

又∵∠AD′C′=∠AB′C′=∠B，

∠AD′D=∠B=∠AB′B，

∴∠AD′C′=∠AD′D，即点D′、D、C′在同一条直线上。

∵∠C′=∠ECB′，∠DEC′=∠B′EC，

∴△CEB′∽△C′ED。

∴B′E∶DE=CE∶C′E=B′C∶DC′，

即B′E∶DE=CE∶C′E=3∶。

设CE=x，B′E=y，

【点评】本题主要考查平行四边形的性质、等腰三角形“三线合一”、相似三角形的性质与判定、解直角三角形的应用等。本题还有多种不同的解法，同学们可以自己尝试一下。

三、三角形与函数

例3（2021·江苏无锡）在平面直角坐标系中，O为坐标原点，直线y=-x+3与x轴交于点B，与y轴交于点C，二次函数y=ax2+2x+c的图像过B、C两点，且与x轴交于另一点A，点M为线段OB上的一个动点，过点M作直线l平行于y轴交BC于点F，交二次函数y=ax2+2x+c的图像于点E。

（1）求二次函数的表达式；

（2）当以C、E、F为顶点的三角形与△ABC相似时，求线段EF的长度；

（3）已知点N是y轴上的点，若点N、F关于直线EC对称，求点N的坐标。

图3

解：（1）在y=-x+3 中，令x=0，得y=3；令y=0，得x=3。

∴B（3，0），C（0，3）。

把B（3，0），C（0，3）代入y=ax2+2x+c，

∴二次函数的表达式为y=-x2+2x+3。

（2）在y=-x2+2x+3中，

令y=0，得x=3或x=-1，

∴以C、E、F为顶点的三角形与△ABC相似，B和F为对应点，如图4。

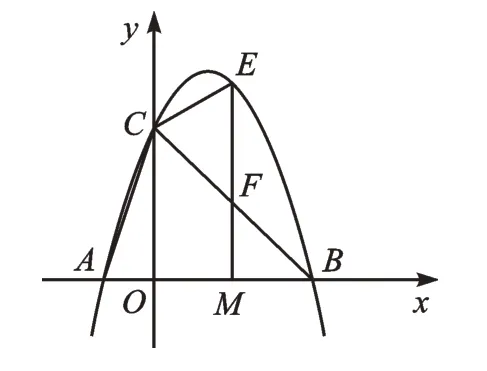
图4

设E（m，-m2+2m+3），则F（m，-m+3），

图5

（3）连接NE，如图5。

∵点N、F关于直线EC对称，

∴∠NCE=∠FCE，CF=CN。

∵EF∥y轴，

∴∠NCE=∠CEF。

∴∠FCE=∠CEF。

∴CF=EF=CN。

【点评】本题的第（2）（3）问涉及三角形相似的判定与性质、对称变换等知识。点M是一个动点，需要引入参数来表示点E和F。解题的关键是先用含字母的代数式表示相关的线段长度，然后在以C、E、F为顶点的三角形与△ABC相似中找到对应点、对应边，根据对应边去分类讨论，最后根据已知列方程求解。解决几何图形中的函数关系的问题，往往要用到几何图形的特征和相似的性质。用含字母的代数式表示未知线段，代入利用相似得到的比例式中求解，是我们常用的方法。