探寻图形本质 获取解题方法

文／孙靓

图形的旋转是初中数学的重难点，也是考查的热点。我们只有对教材例题进行深入分析，探寻图形本质，才能合理利用模型快速切入问题，获得解题思路。

原题呈现（苏科版数学教材九年级下册第60 页例5）如图1，在四边形ABCD中，AC、BD相交于点F，点E在BD上，且

（1）∠1与∠2相等吗？为什么？

（2）△ABE与△ACD是否相似？并说明理由。

图1

【分析】在第（1）问中，根据已知条件，通过三边成比例可证明△ABC∽△AED，得到∠BAC=∠EAD，等式两边同时减去公共角∠EAF，得∠1 与∠2 相等。在第（2）问中，对已知条件进行适当变形，再根据第（1）问结论证明两个三角形相似。详细解答过程见教材。

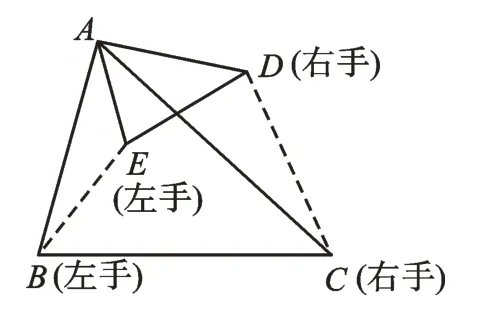
图2

本题中所涉及的基本图形是两个相似的三角形绕着公共顶点旋转形成。如图2，在△ABC和△AED中，我们将点B和点E分别看作两个三角形的左手，将点C和点D分别看作两个三角形的右手，左手与左手相连，右手与右手相连。我们通常将此模型称为“手拉手”模型，以此模型结构为基础的问题可谓是琳琅满目，下面我们一起来看一看。

变式1如图3，在△ABC与△ADE中，∠ACB=∠AED=90°，∠ABC=∠ADE，连接BD、CE。

求证：（1）△ABC∽△ADE；（2）若AC∶BC=3∶4，求BD∶CE为多少？

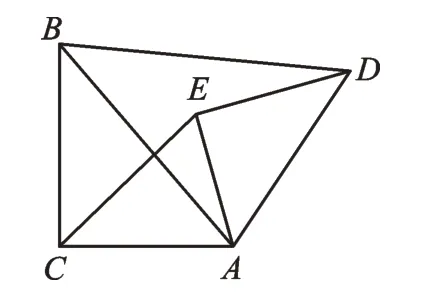
图3

【分析】（1）根据题目给的两组角相等即可得相似；（2）根据（1）中相似可证△AEC∽△ADB，进而可求其相似比。

（1）证明：∵∠ACB=∠AED，∠ABC=∠ADE，

∴△ABC∽△ADE。

（2）解：∵AC∶BC=3∶4，

设AC=3x，则BC=4x。

变式2【问题呈现】如图4，△ABC和△ADE都是等边三角形，连接BD、CE，求证：BD=CE。

图4

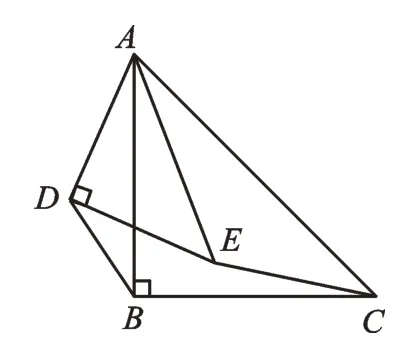
图5

【类比探究】如图5，△ABC和△ADE都是等腰直角三角形，∠ABC=∠ADE=90°，连接BD、CE，请直接写出的值。

【拓展提升】如图6，△ABC和△ADE都是直角三角形，∠ABC=∠ADE=90°，且，连接BD、CE。

图6

【分析】问题呈现：证明△BAD≌△CAE，从而得出结论；类比探究：证明△BAD∽△CAE，进而得出结果；拓展提升：（1）先证明△ABC∽△ADE，再证得△CAE∽△BAD，进而得出结果；（2）在（1）的基础上得出∠ACE=∠ABD，进而∠BFC=∠BAC，进一步得出结果。

解：【问题呈现】

∵△ABC和△ADE都是等边三角形，

∴AD=AE，AB=AC，∠DAE=∠BAC=60°。

∴∠DAE-∠BAE=∠BAC-∠BAE。

∴∠BAD=∠CAE。

∴△BAD≌△CAE（SAS）。

∴BD=CE。

【类比探究】

【拓展提升】

（2）由（1）得△CAE∽△BAD。

“手拉手”模型是解决三角形全等或相似问题常用的模型。大家要多感受此类方法，遇到类似问题要多思考、多总结，长此以往才能达到“会一题，通一类”的效果。