一题多变 拓展创新

文／王涵

在函数图像中求面积问题，因其综合性强，涉及的知识点多，常常出现在中考压轴题中。下面对一道基础题进行变式、拓展，希望同学们能从中体会到基本数学思想的灵活运用。

【例题呈现】如图1，一次函数y=2x-2 的图像与x轴、y轴分别交于A、B两点，求此图像与坐标轴围成图形的面积。

图1

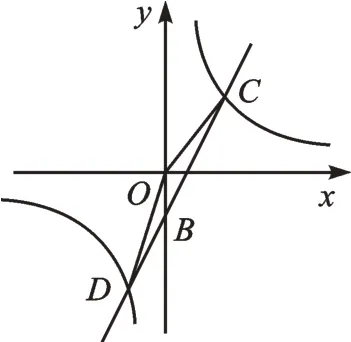
图2

【解析】一次函数的图像与坐标轴围成的是直角三角形，求得两条直角边长即可。由题意得A（1，0）、B（0，-2），易得

【变式一】如图2，一次函数y=2x-2 的图像与反比例函数y=的图像交于C、D两点（C在D右侧），与y轴交于点B，求△COD的面积。

【解析】联立两个函数表达式，可得交点坐标C（3，4）、D（-2，-6），OB=2，则S△COD=。通过本题，同学们要能体悟到，在平面直角坐标系下，常常将不平行或不垂直于坐标轴的线段向平行或垂直于坐标轴方向转化，即“化斜为直”。

【拓展一】点A（m，6m）、B（3m，2n）、C（-3m，-2n）在函数（k≠0）图像上。若S△ABC=2，则k=________。

图3

【变式二】如图4，一次函数y=2x-2 的图像与二次函数y=2x2-4x-10 的图像交于E、F两点（E在F右侧），点E、F下方的二次函数图像上有一个动点P，求△EFP的面积最大值。

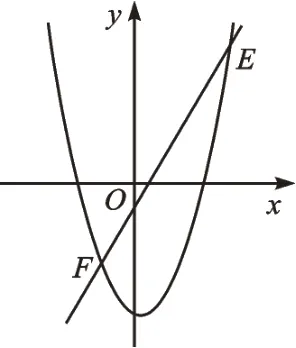
图4

图5

【解析】不难发现这与“变式一”有相似之处。首先，联立两个函数表达式，得到E（4，6），F（-1，-4），过点P作x轴的垂线交EF于点M（如图5）。因为P为动点，那么△EFP的面积随着点P的位置的变化而变化，可以建立△EFP的面积与点P的横坐标之间的二次函数模型。设P（m，2m2-4m-10），则M（m，2m-2），PM=-2m2+6m+8，所以S△EFP=S△MPE+。当时，S△ABE的最大值为。

【拓展二】如图6，二次函数的图像与x轴交于点A和点B（5，0），D（1，3）为顶点，在该图像上是否存在点G，使得△ADG的面积是△BDG的面积的？

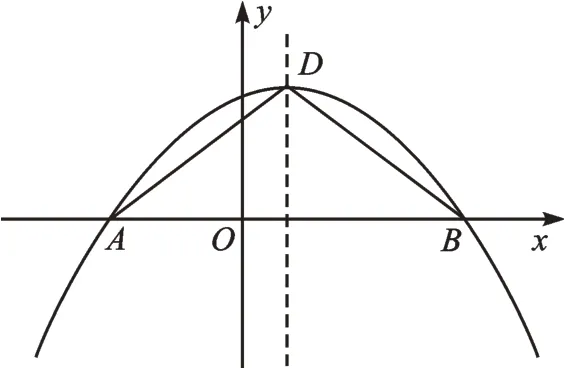
图6

图7