基于轴承变位的大型船舶挠曲轴系振动特性仿真分析

张 聪，李昌平，田亚奇，杨 磊

(1.武汉理工大学 交通与物流工程学院, 湖北 武汉 430070；2.武汉理工大学 船海与能源动力工程学院, 湖北武汉 430070；3.国家水运安全工程技术研究中心, 湖北 武汉 430063)

0 引 言

大型船舶轴系因船体尾部柔性偏大、推进轴系刚性大等因素对外部干扰较为敏感，复杂工作环境易引起轴系固有频率发生变化[1-2]。推进轴系因螺旋桨、设备、部分结构存在集中质量和重力等因素发生挠曲，实际轴线不为一直线。海浪冲击、轴承温度、压载、安装工艺等因素引起的轴承变位改变了轴系的工作状态[3]，导致安装好的轴系在运行过程中出现负荷分布不均、轴承磨损加剧、轴系振动噪声增大等现象，对船舶运行的稳定性和工作的舒适性有较大影响。

针对轴段挠曲、轴承变位、船体变形激励、螺旋桨陀螺效应等对轴系振动特性的影响问题国内外学者开展了大量研究。沈永风等[4]利用Ansys 有限元软件对挠曲轴系横向振动特性分析发现其固有频率比正常轴系小，受剪切变形和剖面转动惯量作用明显。周凌波等[5]指出轴承位置布置、标高变化、轴段挠曲等因素不仅影响到轴系校中状态还对轴系回旋振动响应有着较大的影响。Seo 等[6]利用改进的有限元方法就某30 万吨超大型原油船对中稳定性评估进行了研究，得出吃水变化引起的船体变形是影响轴系各支撑座偏移变形的关键因素。刘江涛等[7]就船舶不同建造阶段船体变形对轴系振动特性进行分析，得出船台下水阶段船体变形对轴系横向振动特性作用明显。刘金林等[8]对舰船直线校中轴系轴承变位引起的回旋振动进行了计算及试验，验证了有限元转子动力学仿真计算方法的有效性。赖国军等[9-10]以后尾轴承负荷最小为目标对轴系试验平台进行了校中优化计算，并对直线校中和合理校中轴系振动响应进行对比分析，建立了校中与减振综合寻优模型。李小军等[11]利用有限元软件Ansys 就尾轴承刚度对计入螺旋桨陀螺效应的轴系回旋振动进行研究，结果表明轴承刚度变化对回旋振动固有频率以及临界转速有一定的影响。Zhang 等[12]进行的试验表明，受到船体变形激励的轴承对轴系振动的影响不可忽视，轴系转速和共振频率设计需考虑船体变形激励频率。马斌等[13]就橡胶尾轴承轴系建立了考虑标高和非线性支撑力的弯曲振动动力学模型，并就标高变化对轴系横向振动进行了数值仿真分析，结果表明尾轴承标高与轴系横向振动关系密切。可以看出，研究大多集中于轴承变位对校中的影响以及直线校中轴系轴承变位的振动特性。大型船舶轴系多采用合理校中且轴承易受船体变形等作用产生变位，现阶段对于考虑轴系初始挠曲的轴承变位振动特性研究较少。

本文以某大型船舶经合理校中后的挠曲推进轴系为研究对象，利用有限元软件Ansys 建立分析模型，分别就轴承不同变位工况下轴系各部分的振动特性和影响因素进行仿真分析。

1 轴系有限元转子动力学

船舶轴系可以简化为多自由度和支撑的弹性系统，其有限元一般动力学方程为：

式中：[M]，[C]和[K]分别为系统质量矩阵、阻尼矩阵和刚度矩阵；{u}，{}和分别为系统位移向量、速度向量和加速度向量；{F(t)}为外界激励。

考虑挠曲[14]和陀螺效应的船舶轴系动力学方程为：

式中：Ω为轴系的转速，[G]为陀螺矩阵，[Kc]为旋转软化刚度效应矩阵，在低转速下影响较小，不计入计算范围，{Q(t)}为轴系挠曲、螺旋桨等激励之和。

2 有限元分析模型

用于分析的某大型船舶推进轴系如图1 所示，包含1 部定距螺旋桨、2 个尾轴承、3 个中间轴承、3 组连接法兰、4 个轴段。几何参数如下：中间轴直径795 mm，尾轴直径975 mm，螺旋桨直径3000 mm，法兰直径1420 mm；中间轴和尾轴长度分别为11000 mm，11000 mm，12880 mm，14165 mm。螺旋桨自重92 580 kg，极转动惯量363 400 kg·m2，径向转动惯量181 700 kg·m2。轴段材质为锻钢，力学参数如下：密度7800 kg/m3，弹性模量207 GPa，泊松比0.25。轴承均为滑动轴承，后尾轴承及中间轴承刚度均为9.81×108N/m，前尾轴承刚度为1.9×108N/m，阻尼系数为1.0×103。

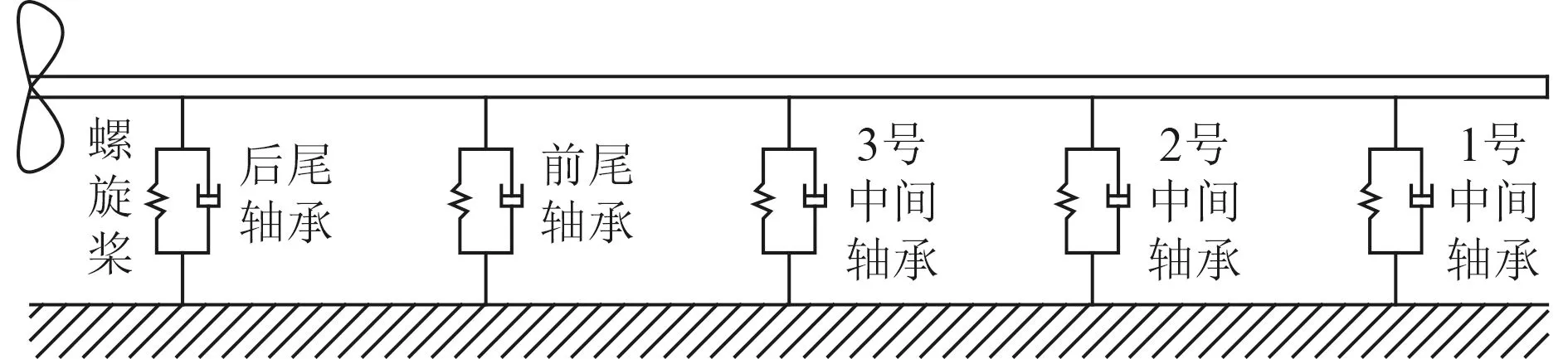
图1 某大型船舶推进轴系示意图Fig.1 Schematic diagram of propulsion shafting of a large ship

为建模和计算方便，对推进轴系进行适当简化。轴段和连接法兰均采用六自由度梁单元Beam188模拟，不同直径轴段通过设置不同梁截面参数表征；滑动轴承均简化为水平和垂直2 个方向的弹簧单元Combin14，弹簧单元不和轴相连的一端自由度全约束模拟和基座接触；螺旋桨简化为带有3 个方向的集中质量Mass21 单元，作用点为几何中心。轴系受到重力作用，G=9.81 m/s2。

轴系有限元模型原点为螺旋桨，自螺旋桨向主机端建模。取坐标轴X方向为轴向，Y方向为垂直方向，Z方向为水平方向，遵循右手法则。通过Ansys 创建的考虑初始挠曲的推进轴系合理校中有限元模型如图2 所示。

图2 考虑挠曲的推进轴系有限元模型Fig.2 Finite element model of propulsion shafting considering deflection

3 仿真分析及讨论

轴系安装和运行过程中，轴承位置不可避免地因外部因素产生一定的变化，轴承位置的变化直接影响到轴系载荷分配和校中状态，不良的工作状况又会引起轴系振动。考虑到螺旋桨的悬臂作用和后尾轴承运行时复杂的环境工况，后尾轴承更容易和频繁地发生变位，取后尾轴承为主要变位轴承对变位引起的轴系振动特性进行有限元分析。

3.1 轴承不同变位工况下轴系固有频率

针对前面建立的有限元模型，考虑陀螺效应并调整后艉轴承垂直方向位置（向上变位为正，向下为负），利用QR 阻尼法进行模态分析得到不同变位工况下前3 阶的正逆回旋固有频率，如表1 所示。

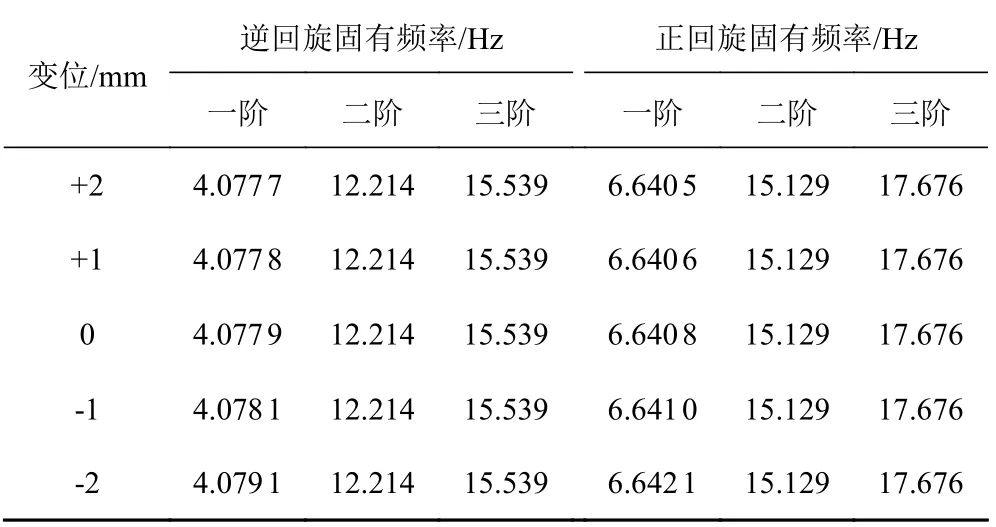
表1 后尾轴承不同变位下计入陀螺效应的轴系固有频率Tab.1 Shafting natural frequencies taking into account the gyroscopic effect under different displacements of the rear stern bearing

可以看出，轴承变位主要对一阶固有频率产生影响，但各变位工况下频率变化较小，二阶、三阶固有频率则没有变化。同阶次正逆回旋固有频率因陀螺效应不同，陀螺力矩为正值时，轴的弯曲刚度增大，轴系固有频率增大；反之，则轴系固有频率降低。

3.2 轴系在轴承不同变位工况下的振动分析

船舶航行时，螺旋桨在船尾不均匀伴流场中受水动力作用产生的激振力和力矩通过轴系传递给船体。通过在螺旋桨节点处施加Fy，Fz，My，Mz方向的力和力矩模拟轴系运行时受到的尾部激振力，考虑Coriolis 效应并施加轴向100 r/min 的转速。应用有限元转子动力学对轴承不同变位方向、变位大小和变位位置3 种工况下轴系的振动响应进行仿真分析。

1）轴承变位方向对轴系振动的影响

取后尾轴承同等变位幅值不同垂直变位方向对轴系振动响应的影响进行分析，分别计算轴系在后尾轴承抬高2 mm、降低2 mm 和初始安装工况下的振动响应。

由图3 的振动响应曲线可以看出，在低频段后尾轴承无论是向下变位还是向上变位振动响应都比初始安装工况大，说明轴承变位改变了轴承和轴系工作状态，振动响应增大；中频段图3(a)中向下变位的振动响应小于初始安装状况，图2(b)中3 种工况振动响应则变化不大。不同变位方向即使是同等幅值大小的轴承变位引起的振动响应也不同，在该转速和变位工况下向下变位显然比向上变位引起的振动响应更大。以一阶振动响应为例，图3(a)中振动响应-2 mm 变位工况比+2 mm 变位工况大15.4 dB，图3(b)中振动响应-2 mm 变位工况比+2 mm 变位工况大15.08 dB，显然后尾轴承向下变位引起的轴承工作状态变化和振动响应更大。

图3 不同变位方向下轴承振动响应Fig.3 Bearing vibration response under different displacement directions

2）轴承变位大小对轴系振动的影响

选取后尾轴承向上变位+2 mm，+1 mm 和初始安装3 种工况就轴系在后尾轴承不同变位幅值大小下的振动响应进行仿真分析。

由图4 的振动响应曲线可以看出，后尾轴承同变位方向（向上变位）不同变位幅值大小下振动响应与轴承变位幅值大小成正比。以一阶振动响应为例，图4(a)中+2 mm 和+1 mm 变位工况振动响应分别比初始变位工况振动响应大101.47 dB 和87.48 dB，图3(b) 中+2 mm 和+1 mm 变位工况振动响应相比初始变位工况振动响应变化80.32 dB 和66.06 dB。显然轴承变位幅值越大，扰动越大，振动响应变化也越大。

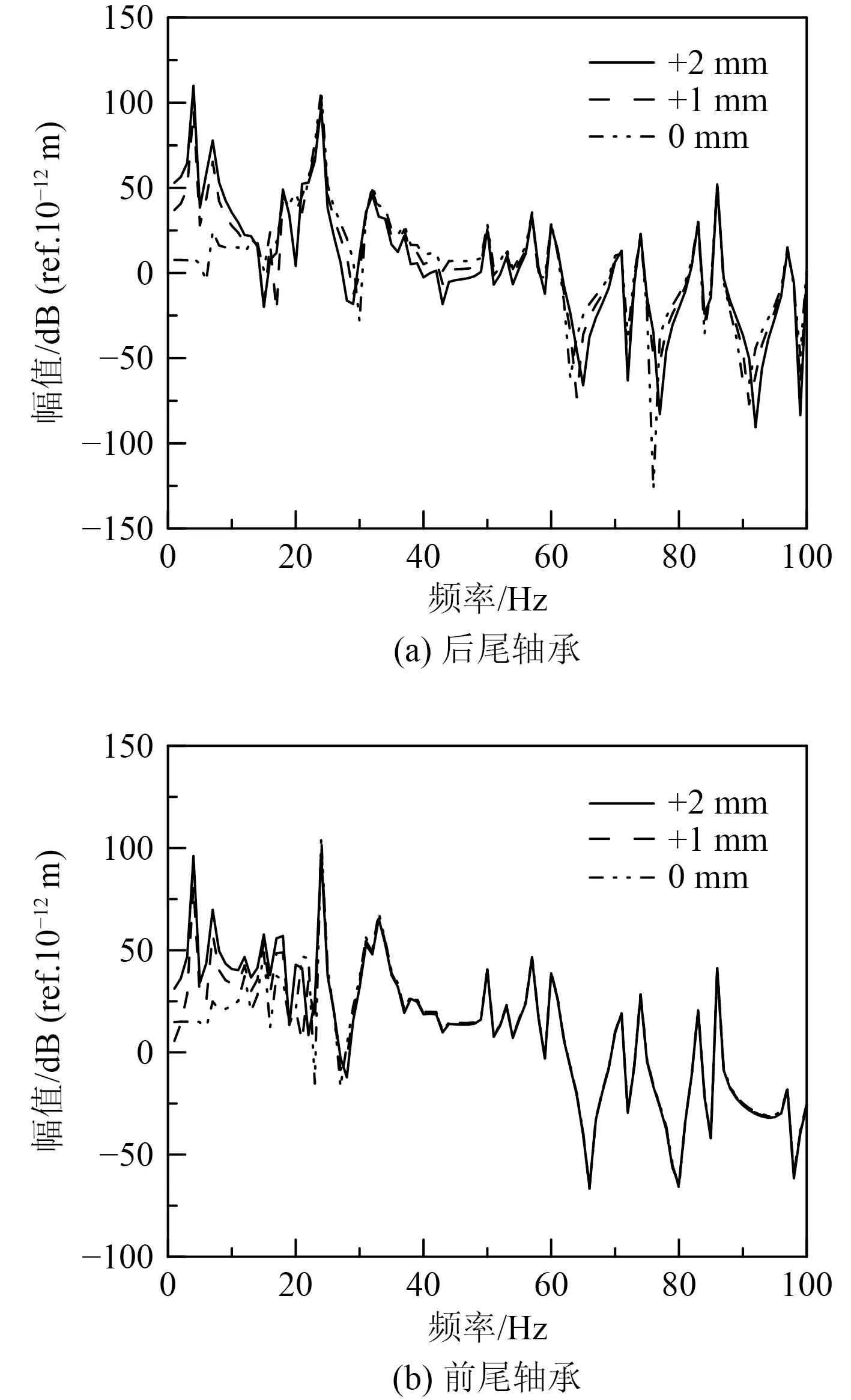
图4 不同变位幅值大小下轴承振动响应Fig.4 Bearing vibration response under different displacement amplitudes

3）不同位置轴承变位对轴系振动的影响

选取靠近前尾轴承的3 号中间轴承，分析2 个不同位置轴承同样变位-1 mm 变位时对轴系振动的影响。

从图5(a)和图5(c)可以看出，对于后尾轴承处的响应点，后尾轴承变位引起的振动响应比3 号中间轴承变位引起的振动响应大；而对于3 号中间轴承处响应点，3 号中轴承变位引起的振动响应比后尾轴承变位引起的振动响应小。表明即使同为变位轴承处轴承变位引起的振动响应，尾轴承变位相比中间轴承变位影响更大，3 号中间轴承因为靠近尾部受到后尾轴承变位引的振动响应相比自身轴承变位响应变化更大。

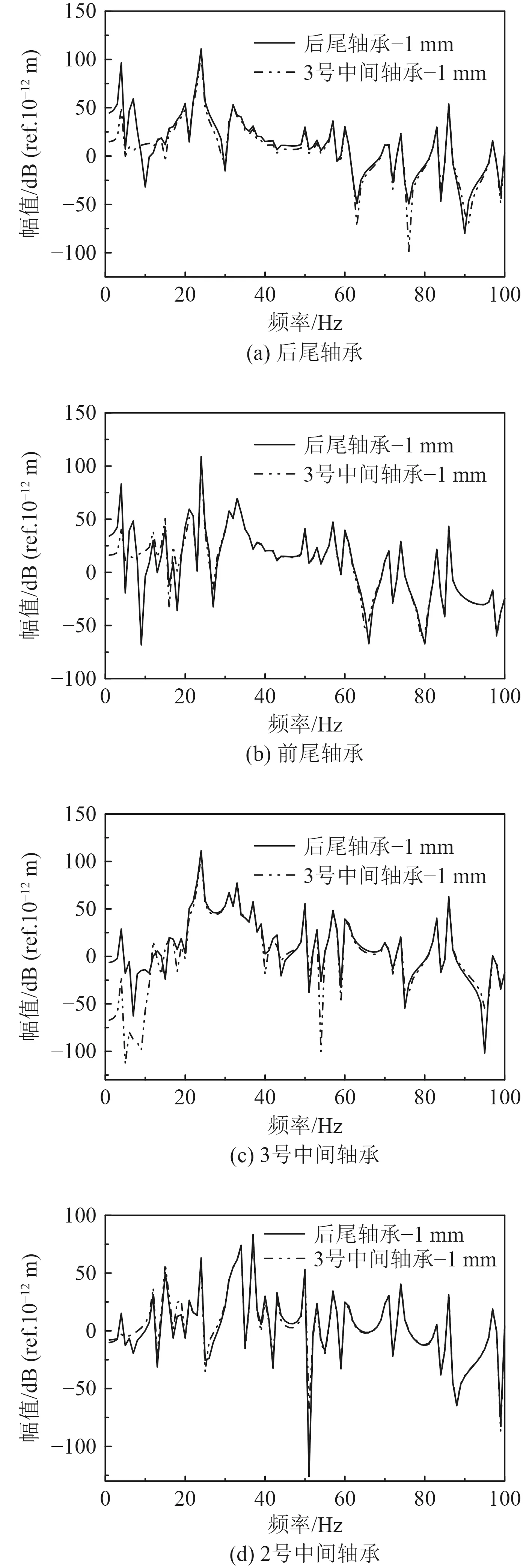
图5 不同位置下轴承振动响应Fig.5 Bearing vibration response at different positions

图5(b)为处于两变位轴承中间的前尾轴承的振动响应曲线，尽管后尾轴承以及3 号中间轴承和前尾轴承之间的跨距几乎相同，但可以看出后尾轴承变位引起的前尾轴承振动响应更大，一方面是因为后尾轴承所处轴段挠曲程度更大，另一方面后尾轴承更靠近螺旋桨受陀螺效应影响更大。

图5(d)为不同位置轴承变位后2 号中间轴承处的振动响应曲线，可以看出3 号中间轴承变位引起的该点振动响应比后尾轴承变位引起的大，说明响应点振动响应大小与响应点距变位轴承的间距成反比，距变位轴承越近振动响应越大。

3.3 轴承变位前后轴系振动影响因素分析

轴系转速和轴承刚度是轴系设计需要考虑的重要参数同时也是影响轴系振动的因素，轴系依照设计建造和安装完成后这些参数一般不会改变，有必要就这些参数对船体变形等激励引起轴承变位导致的振动响应的影响进行探讨。本文分别就后尾轴承变位前后轴系在不同转速和轴承刚度工况下的振动响应进行仿真分析。

1）转速对轴承变位前后轴系振动的影响

保持各轴承刚度为9.81×108N/m 不变，就后尾轴承不同变位工况下的轴系在100 r/min，300 r/min 和500 r/min 转速下的振动响应进行仿真，得到如图6 所示后尾轴承不同变位工况下各转速工况的振动响应曲线。

图6 不同变位及转速下的轴承处振动响应Fig.6 Vibration response of bearing at different displacements and rotational speeds

可以看出，后尾轴承各变位工况下的振动响应大小皆与转速成正比，转速越高轴承变位幅值变化对振动响应的影响越明显。图6(a)中无论哪个变位工况的振动响应曲线都是500 r/min 对应的最大，300 r/min 次之，100 r/min 最小；图6(b) 中轴系转速为100 r/min时，各变位工况的振动响应曲线最为接近，变化趋势几乎相同，转速为500 r/min 时5 条响应曲线间差异较大。一方面表明轴系转速越高，陀螺效应影响越大，另一方面高转速下轴系对轴承位置变化更敏感。

2）轴承刚度对轴承变位前后轴系振动的影响

轴系转速取100 r/min，就后尾轴承不同变位工况下的轴系在不同轴承刚度下的振动响应进行分析。除前尾轴承外各轴承刚度分别取K1=9.81×107N/m，K2=9.81×108N/m，K3=9.81×109N/m，前尾轴承取与其他轴承对应量级刚度。后尾轴承不同变位工况下各刚度工况的振动响应曲线如图7 所示。

图7 不同变位及刚度下的轴承处振动响应Fig.7 Vibration response of bearing under different displacement and stiffness

可以看出，后尾轴承各变位工况下的振动响应随着轴承刚度的增大而减小，刚度变化越大轴承变位幅值大小对振动响应的影响越大。图7(a)中各变位工况下的振动响应曲线都是较小刚度K1对应的最大，轴系选定刚度K2次之，较大刚度K3对应的响应最小；图7(b)中低频部分不同刚度下轴承变位对振动响应都比较大，其他频段K2刚度下各变位工况的振动响应曲线较为接近，K1刚度下向下变位-2 mm 对应的响应曲线相比其他4 条响应曲线变化较大，K3刚度下各变位振动响应曲线间变化都比较大。说明轴系设计选定K2刚度较为合理，能有效减小变位的影响，较大刚度轴承对变位引起的振动作用明显。

4 结 语

本文利用Ansys 建立大型船舶合理校中的挠曲推进轴系有限元模型。对轴承不同变位工况下轴系的振动响应进行动力学仿真分析，并对转速、轴承刚度两影响因素和变位综合作用下的振动响应进行讨论，得出以下结论：

1）轴承变位对轴系振动的影响不是单一因素决定的，需要考虑轴系转速、轴承刚度、陀螺效应等因素，振动响应大小与变位幅值也不是简单的线性关系，轴承变位大小、方向、位置等有不同程度的影响。

2）合理校中后的挠曲轴系通过轴承变位可以改变校中状态，但振动响应会随之变化且响应大小与轴承变位幅值成正比，同等变位幅值不同方向的轴承变位振动响应不同。尾部轴系挠曲更大且更靠近螺旋桨轴承变位引起的振动响应最大，距离变位轴承越远的轴承振动响应受到变位的影响越小。

3）轴承变位前后，轴承振动响应大小与轴系转速呈正相关，转速越高轴承变位幅值变化对振动响应的影响越大；不同变位工况下轴承刚度越大振动响应越小，合理的轴承刚度可减小轴承变位对轴系振动响应的影响。