不完备广义多尺度决策系统的逐步最优尺度选择
2023-05-05程云龙吴成英张清华
牟 琼,程云龙,,吴成英,张清华
(1.重庆邮电大学 数理学院,重庆 400065;2.重庆邮电大学 计算机科学与技术学院,重庆 400065;3.重庆邮电大学 计算智能重庆市重点实验室,重庆 400065)
0 引 言
粒计算是信息处理的一种新的计算范式。美国著名控制论专家Zadeh[1]于1979年首次提出了模糊信息粒。中国张钹院士[2]指出“人类智能的一个公认特点就是人们能从极不相同的粒度上观察和分析同一问题”。波兰科学家Pawlak[3]提出的粗糙集是粒计算的一个具体模型,已被广泛应用于人工智能、机器学习、模式识别、数据挖掘等领域。
现实生活中,信息不完备现象广泛存在。Kryszkiewicz[4]首次提出了基于容差关系的粗糙集模型以研究不完备信息系统。Stefanowski[5]等提出了量化容差关系,利用已知信息的相同程度去刻画对象之间的相似程度。针对不一致不完备决策系统,Qian等[6]提出了基于辨识矩阵的属性约简方法。文献[7-10]分别研究了不完备信息系统中的属性约简。然而,上述不完备信息系统描述的是固定尺度下的对象信息,即每个对象在给定属性下只能取唯一的属性值。显然,这种固定粒度框架下的知识挖掘方法已远远不能满足实际应用的需要。
同一个对象通常可用不同尺度来测量[11]。针对这种多尺度标记的层次数据,Wu和Leung[12]首次提出了多尺度信息系统,被称为Wu-Leung模型。在多尺度信息系统中,属性和尺度是决定粒度大小的2个关键因素。由于已经有很多经典的算法可处理单尺度决策系统的属性约简,因而现有的多尺度研究更多关注最优尺度选择问题。例如,完备多尺度决策系统的最优尺度选择[13-14]与局部最优尺度选择[15],不完备多尺度决策系统的最优尺度选择[16-17]。然而,在上述多尺度决策系统中,所有属性被假定具有相同的尺度个数。Li和Hu[18]假设不同属性可以取不同的尺度个数,提出了完备广义多尺度信息系统,并给出了2种方法求所有最优尺度组合。针对完备广义多尺度信息系统,Li等[19]提出了逐步最优尺度选择方法,Huang等[20]研究了决策属性为多尺度的情形,Huang等[21]研究了属性值为直觉模糊数的情形,Zhang等[22-24]探究了尺度组合间的偏序关系及其性质,提出了求所有最优尺度组合的三支决策模型,该模型显著降低了现有算法的时间、空间复杂度。
然而,鲜有文献研究不完备多尺度决策系统的最优尺度选择算法,且现有的多尺度研究方法不一定能获得全局最优尺度组合。该研究的主要目的是设计一个高效的、不完备广义多尺度决策系统的最优尺度组合选择算法。首先,介绍了不完备广义多尺度决策系统及其上下近似集的性质;其次,采取属性约简与尺度选择同步优化策略,定义了一个新的尺度组合,以获得全局最优尺度组合;最后,从提高一致性判断效率和减少一致性判断次数2个角度,分别设计了求相容类的快速算法和不完备广义多尺度决策系统的逐步最优尺度选择算法。
1 基础知识
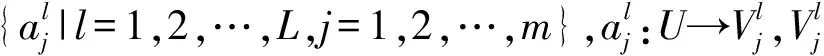

(1)
设B⊆A,l∈{1,2,…,L},记Bl所导出的相容关系TBl和相容类TBl(x)分别为
TBl(x)={y|(x,y)∈TBl},x∈U。

显然,任何一个不完备多尺度决策系统
可分解为L个单尺度决策系统
设Rd={(x,y)∈U×U|d(x)=d(y)},决策属性d对论域U的划分U/Rd={D1,D2,…,Dr}。若RAl⊆Rd,则称Sl是一致的,否则称为不一致。特别地,若RAI⊆Rd,则称S是一致的。
定义2[17]设S=(U,A∪{d})为不完备多尺度决策系统,若Sl是一致的,且当l≥2时,Sl-1是不一致的,则l是S的最优尺度。
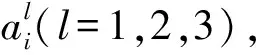

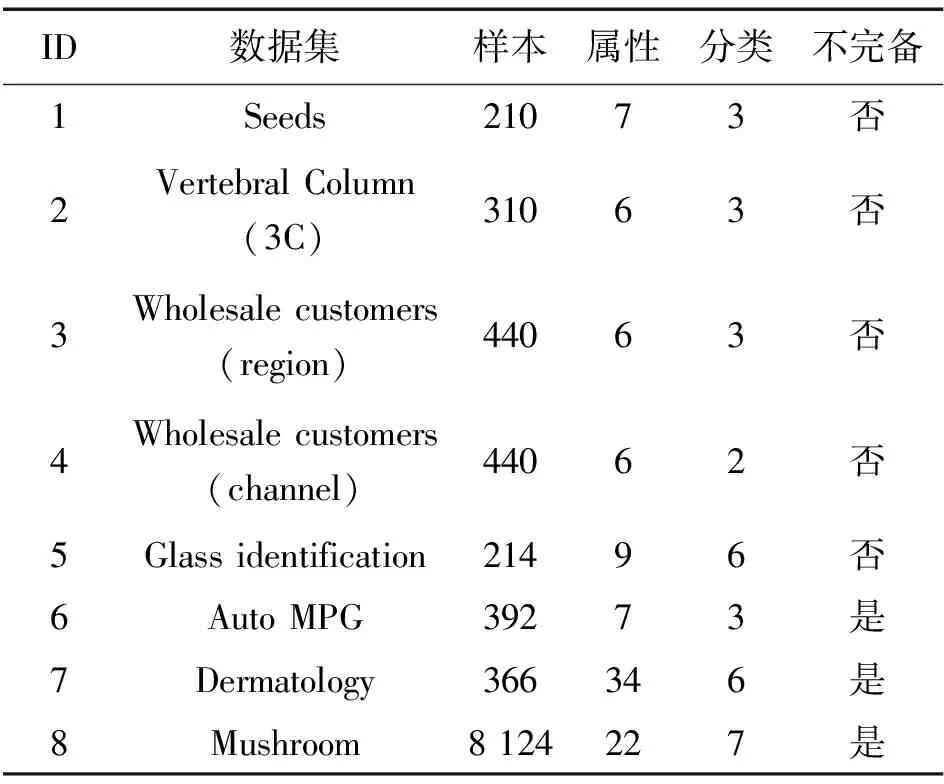
表1 不完备多尺度决策系统
虽然,S可分解为3个单尺度决策系统:S3,S2,S1,其中,S2如表1中阴影部分所示。由表1可知:
U/Rd={{x1,x2},{x3,x4,x5,x6,x7,x8}},
U/TA3={{x1},{x2},{x3},{x4},{x5},{x6},{x7},{x8}},U/TA2={{x1,x2},{x3},{x4},{x5},{x6,x7},{x8}},
U/TA1={{x1,x2,x3},{x1,x2,x3,x8}{x4,x6},
{x5,x6,x7},{x4,x5,x6,x7},{x3,x8}}。
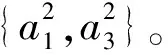
U/TB={{x1,x2},{x3,x5,x6},{x4,x6},{x6,x7,x8},{x3,x4,x5,x6,x7,x8}}⊆U/Rd,
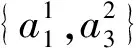
例1表明先由定义2得到最优尺度,然后对最优尺度所对应的单尺度决策表进行属性约简,不一定能获得最优粒度。究其原因:①因为定义2要求所有属性的尺度必须相等;②尺度选择后属性约简的这种串行处理方式所致。
2 不完备广义多尺度决策系统
针对不完备广义多尺度决策系统,本节提出一个新的尺度组合以同步优化尺度选择与属性约简。
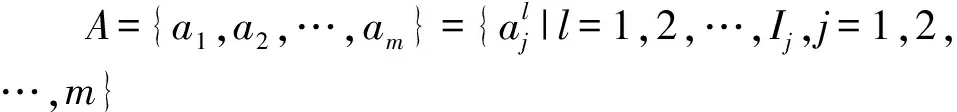
定义4S=(U,A∪{d})为不完备广义多尺度决策系统,lj为属性aj所选取的尺度,0≤lj≤Ij,且lj=0表示属性aj未被选择, 则全体属性所选取的尺度组成的向量K=(l1,l2,…,lm)称为S的一个尺度组合。最细尺度组合I=(I1,I2,…,Im),最粗尺度组合0=(0,0,…,0)。所有尺度组合所构成的集合称为尺度空间Ω,即
Ω={K=(l1,l2,…,lm)|0≤lj≤Ij,
j=1,2,…,m}。
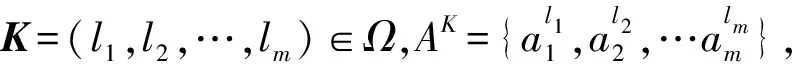
(2)
TAK(x)={y|(x,y)∈TAK},x∈U
(3)
于是,X(X⊆U)关于AK的下近似和上近似分别为
(4)
(5)
且D={d}关于AK的正域为
(6)
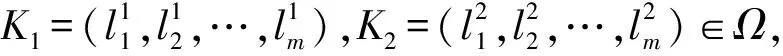
由(1)—(3)式,易知如下性质成立。
性质1设I≥K1K20,则
1)TAI⊆TAK1⊆TAK2⊆TA0;
2)TAI(x)⊆TAK1(x)⊆TAK2(x)⊆TA0(x),x∈U。
性质2表明,给定一个不完备广义多尺度决策系统,若尺度组合K逐渐变粗,则由K导出的相容类逐渐变大。
性质2设S=(U,A∪{d})为不完备广义多尺度决策系统,X,Y⊆U,K,K1,K2∈Ω,则

显然,对∀K∈Ω,可由S=(U,A∪{d})导出一个单尺度决策系统SK=(U,AK∪{d})。若SK满足POSAK(D)=POSAI(D),则称SK是一致的,并称K为一致尺度组合。若POSAK(D)=U,则称S是一致的,否则称S是不一致的。
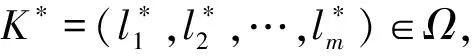
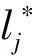
由定义5,性质4成立。
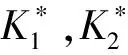
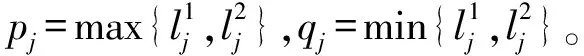
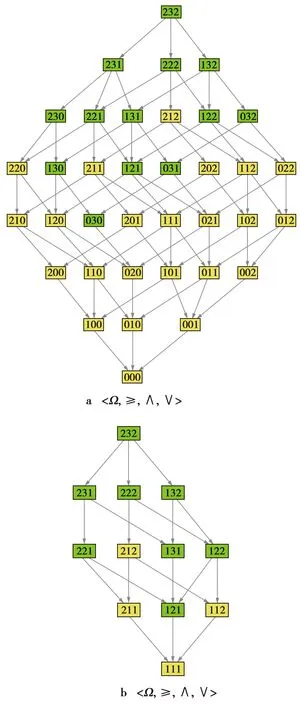
图1 尺度格Fig.1 Scale lattice
3 逐步最优尺度选择
提出一个快速的相容类算法和不完备广义多尺度决策系统的逐步最优尺度选择算法。
在不完备决策系统中,需要求SK的相容类以判断SK是否一致。针对两两比较法求相容类存在时间复杂度高的缺陷,提出了基于排序和粒运算的相容类求法。考虑到同一个等价类中任意2个对象的相容类相等,即对∀xi,xj∈[x]AK,则TAK(xi)=TAK(xj)。受此启发,首先将论域U分为不含缺失值的对象集U1和含缺失值的对象集U2;然后利用排序求U1的等价类[22],记作{X1,X2,…,Xs},并将每一个等价类标记为一个新的对象;最后利用两两比较法判别U2中的对象与粒子{X1,X2,…,Xs}的相容关系,以及U2中对象间的相容关系。具体流程见算法1。
算法1基于排序与粒运算的相容类算法
输入:单尺度决策系统SK=(U,AK∪{d})
输出:SK的相容类Sim
Step 1:Sim←{};
Step 2:将U分解为不含缺失值的对象集U1和含缺失值的对象集U2={xj1,xj2,…,xjr};
Step 3:利用排序求U1关于AK的等价类,记
U1/RAK={X1,X2,…,Xs};
Step 4:Sim(i)←Xi,i={1,2,…,s},
Sim(s+i)←xji,i={1,2,…,r};
Step 5: 求xji∈U2的相容类
fori=1:r
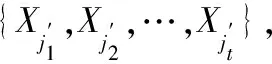
Sim(u)←xji,u∈Ind;
forv=i+1:r
ifxjv与xji满足相容关系
Sim(s+i)←xjv;
Sim(s+v)←xji;
end
end
end
Step 6: 输出Sim
例2(续例1) 设K=(1,0,2),根据表1可知,U1={x1,x2,x4,x5,x7,x8},U2={x3,x6}。在K尺度下,对U1按属性值升序排列可得U1/RAK,即
U1/RAK={{x1,x2},{x4},{x7,x8},{x5}}=
{X1,X2,X3,X4}。
于是
X1:Sim(1)={x1,x2},X2:Sim(2)={x4},
X3:Sim(3)={x7,x8},X4:Sim(4)={x5},
x3:Sim(5)={x3},x6:Sim(6)={x6}。
在K尺度下,x3=(*,3)与粒子X4,与对象x6满足相容关系,故将X4中的对象以及对象x6添加到Sim(5)中,即Sim(5)={x3,x5,x6}。同时,相容关系的对称性有Sim(4)={x5,x3},Sim(6)={x6,x3}。
同理,x6=(4,*)与粒子X2,X3,X4相容,故Sim(6)={x6,x3,x4,x7,x8,x5},Sim(2)={x4,x6},Sim(3)={x7,x8,x6},Sim(4)={x5,x3,x6}。
因此,由AK导出的相容类为
Sim(1)={x1,x2},Sim(2)={x4,x6},
Sim(3)={x7,x8,x6},Sim(4)=Sim(5)={x5,x3,x6},Sim(6)={x6,x3,x4,x7,x8,x5}。
算法1的时间复杂度分析:步骤2的时间复杂度为O(m|U|),其中|·|表示集合的基数;步骤3的时间复杂度为O(m|U1|);由于|Xi|<<|U1|,故步骤5的时间复杂度近似为O(m|U2|2);其余步骤的时间复杂度为常数。因此,算法1的时间复杂度为O(m(|U|+|U2|2))。通常|U2|<|U|,故算法1的时间复杂度低于两两比较的时间复杂度O(m|U|2)。
当属性或尺度个数递增时,尺度组合个数将急剧增加。针对该情形,Li等[19]提出了逐步最优尺度选择算法求完备多尺度决策系统在Ω+上的最优尺度组合。然而,在计算多尺度属性重要度时,需要计算每一个属性在每一个尺度下的重要度,对高维数据情形,存在耗时较高的缺陷。同时,若属性在最细尺度下的重要度较小,则该属性在粗尺度下的重要度更小。因此,可用最细尺度组合下的属性重要度代替多尺度属性重要度。
设S=(U,A∪{d})为不完备广义多尺度决策系统,Kj=(I1,…,Ij-1,0,Ij+1,…,Im),定义属性aj在S中的重要度为
sig(aj,A,D)=γAI(D)-γAKj(D),
(7)
不完备广义多尺度决策系统的逐步最优尺度选择算法见算法2。
例3详细说明了算法2的具体流程。
例3(续例1)属性a1,a2,a3的重要度分别为
因此,属性排列顺序为(a2,a1,a3)。
令K=I=(3,3,3)。
算法2不完备广义多尺度决策系统的逐步最优尺度选择
输入:不完备多尺度决策系统S=(U,A∪{d})
输出:最优尺度组合(optimal scale combination,OSC)
Step1:根据(6)式,计算属性重要度,并按升序排列,不妨假设为(aj1,aj2,…,ajm);
Step2:K←I=(I1,I2,…,Im);
Step3:fori=1:m%m为属性个数
K(ji)←0,%令属性aji的尺度为零;
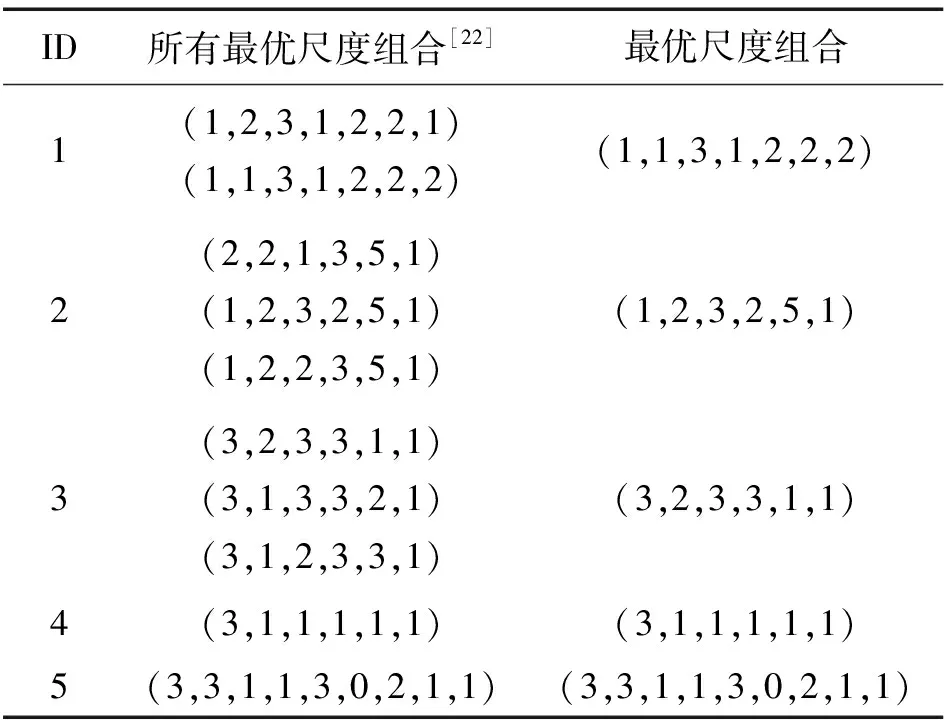
whileK(ji) ifSK一致 break; else K(ji)←K(ji)+1; end end end Step4:OSC←K。 首先考虑属性a2:将K中属性a2的尺度变为最粗尺度,即K=(3,0,3)。SK是一致的,故属性a2的最优尺度为0; 其次考虑属性a1:将K中属性a1的尺度变为最粗尺度,即K=(0,0,3)。SK是不一致的,于是属性a1的尺度加1,即K=(1,0,3);此时,SK是一致的,故属性a1的最优尺度为1。 最后考虑属性a3:将K中属性a3的尺度变为最粗尺度,即K=(1,0,0)。SK是不一致的,于是属性a3的尺度加1,即K=(1,0,1)。SK是不一致的,于是属性a3的尺度继续加1,即K=(1,0,2)。此时,SK是一致的,故属性a3的最优尺度为2。 因此,K*=K=(1,0,2)是S的最优尺度组合。 显然,算法2的空间复杂度为O(m|U|)。 数据集来源于UCI机器学习数据库,数据集详细描述如表2所示,其中数据集1-6是文献[18-19,22-24]的实验数据集。实验环境为Windows XP操作系统, Intel(R) Core(TM) i7, CPU 1.80 GHz,程序通过Matlab7.0软件实现。 表2 数据集描述 数据集1-8均是单尺度决策系统,利用Li等[19]提出的方法将单尺度决策系统转换为多尺度决策系统。同时,数据集1-5是完备决策系统,为了得到不完备决策系统,采用先随机选取对象,再随机选取属性和尺度的方法,将部分属性值改为缺失值,缺失率α=0.1。 在完备信息的情形下,Zhan等[22]提出了基于三支决策和哈斯图求所有最优尺度组合的方法。对完备数据集1-5,算法2与文献[22]所求得的最优尺度组合如表3所示。由表3可看出,算法2所得到的最优尺度组合是文献[22]所得到的全体最优尺度组合中的一个。数值实验表明由算法2求得的结果是有效的。 表3 完备数据集1-5的最优尺度组合 图2 2种求相容类方法的运行时间Fig.2 Running time of two methodsfor finding similar classes 对数据集1-8,2种方法所得到的最优尺度组合及其运行时间如表4所示,其中“-”表示在24小时内未求得最优尺度组合。 由表4可看出,大多数情形下,2种方法所得到的最优尺度组合是不同的,L-H算法所得到的尺度之和更小。例如,对数据集1,L-H算法得到的尺度之和为12,算法2得到的尺度之和为13,而对数据集2、3、4、6,2种算法得到的尺度之和是相等的。然而,算法2的运行时间显著低于L-H算法的运行时间,例如:对数据集4,L-H算法的运行时间是39.6 s,而算法2的运行时间是2.3 s;数据集5有4 148 928个尺度组合,L-H算法在24 h内未得到最优尺度组合;对数据集7和8, 运行L-H算法时,系统提示内存不足。数值实验表明,算法2能在一个可容忍的时间内获得一个满意解。 表4 最优尺度组合与运行时间 针对传统的先尺度选择后属性约简的串行处理方式有可能得不到全局最优尺度组合的问题,提出了新的尺度组合以同步优化尺度选择与属性约简。针对缺乏高效的不完备多尺度决策系统的最优尺度选择算法问题,设计了一个高效的求相容类算法,在此基础上提出了逐步最优尺度选择算法以快速地获得不完备广义多尺度决策系统的一个最优尺度组合。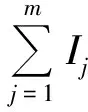
4 数值实验
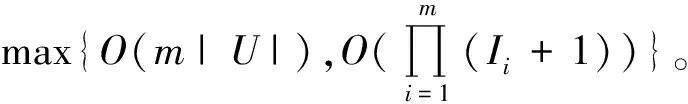
5 结 论
