小型无人机遥控器信号跳频参数估计方法

徐亚军,唐文波,鲁合德,司成可

(中国民用航空飞行学院, 四川 广汉 618307)

0 引言

近年来,无人机滥用和黑飞现象时有发生,导致安全事故层出不穷[1]。雷达[2]、声学[3]、光电[4]等检测技术成为了检测无人机目标的主流手段。但是上述检测技术均存在其不足,而无线电检测[5]是利用无人机与遥控器之间的控制信号来检测无人机目标,具有监测距离远、受环境影响小等显著特点。

跳频扩频信号是典型的非平稳信号,时频分析法[6]凭借对非平稳信号的分析拥有强大的处理能力成为了无人机信号检测的主流方法。在该类方法中,线性时频分析法运算复杂度低、实时性高,但无法同时获得高时间、频率分辨力[7]。非线性时频分析法具有良好的时频聚集性,但存在运算量与时频聚集性无法兼得的问题[8-10],这严重影响了参数估计的性能。近年来,许多组合时频估计参数算法被相继提出,如文献[11]将STFT和SPWVD相组合提出了一种新的时频分析方法,参数估计性能得到了提升,但是受噪声影响大。文献[12]在时频分析基础上引入门限降噪策略对噪声进行抑制,提高了信号时频参数估计性能,但是设置的静态门限难以应对复杂动态变化的信号检测场景。

考虑当前各类跳频信号参数估计方法均存在各自不足,基于频域互相关运算获得相邻时隙采样信号的频域互相关特征,通过引入逻辑回归、门限自适应去噪算法完成对无人机遥控器信号参数的估计,提高了跳频信号特征参数的估计性能。

1 信号模型与算法介绍

1.1 跳频信号时域模型

小型无人机遥控器信号普遍采用跳频通信技术,典型的跳频信号时域模型[13]如下:

(1)

其中:

(2)

式(1)中的K为可观测到的跳频次数;ak(t)表示幅度;式(2)中,t′=t-(k-1)TH,sk(t)、fk、φk分别表示第k个跳频信号分量及其瞬时载波中心频率和初始相位;TH为每跳驻留时长。

在均值为0方差为σ2的复高斯白噪声噪声场景中,经过对信号离散采样后的N点离散信号观测值建模为

g(n)=s(n)+v(n),n=1,2,…,N

(3)

1.2 逻辑回归算法

逻辑回归分类器本质上是一组权值,与支持向量机、神经网络等自主优化训练的学习算法相比,其在模型训练、预测耗时上都占有很大优势。逻辑回归模型[14]的数学表达式为

(4)

式中:θ为模型权值;x为输入序列;f(θ;x)为模型预测的概率值,取值范围为(0,1)。

根据实际需要设置阈值,通过判断f(θ;x)是否超过阈值确定预测结果的所属类别。利用最大似然方法对θ进行估算,它是一个高阶可导的凸函数求解问题,本文中采用梯度下降法求最优解。

1.3 门限自适应算法

对离散信号g(n)进行傅里叶变换后得到G(n),则去噪算法的门限值[15]为

(5)

由于噪声能量较小且分布在整个频域范围内,而跳频信号的能量则相对比较集中,因此存在一个门限值能区分信号和噪声,但是在不同场景下信号和噪声的能量差异也不同,所以门限值是变化的,因此本文中引入门限自适应去噪算法去除噪声。具体步骤如下:

1) 设定w在区间[1,10)以0.1为步长取值,并根据式(5)计算出门限值th(i),其中1≤i≤90。

2) 通过式(6)统计大于门限值th(i)的点数:

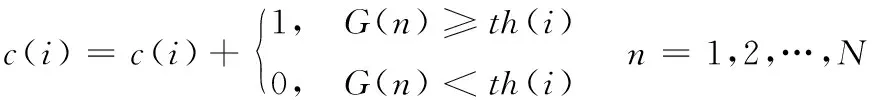
(6)

3) 计算c(i)二次差分结果中首次最接近零值的点,将其对应的权重w代入式(5)得到门限值。

2 小型无人机遥控器信号跳频参数估计方法

同一架无人机遥控器信号的每跳信号具有相同带宽,利用频域互相关处理可在频域上获得高相似性的能量分布特征,因此基于该特性可以估计出无人机遥控器信号跳频参数。为展示该特性,基于前文所述的跳频信号模型生成仿真数据,设无人机遥控器信号的频率范围为10～250 kHz,频率间隔为50 kHz,每跳信号驻留时长为10 ms,采样频率为900 kHz,采样时长为500 ms,信号划分时隙为1 ms,信噪比为9 dB。计算了无人机遥控器信号与噪声的、相邻跳信号的以及同一跳信号不同时隙的频谱图及其频域互相关结果。

如图1所示,当相邻时隙信号的前一时隙和后一时隙分别为噪声、信号时,两者的频域互相关结果不会出现明显峰值,很显然此时相邻时隙信号不是同一跳无人机遥控器信号。图2中,当相邻时隙信号的前一时隙为前一跳信号的末段信号,后一时隙为后一跳信号的首段信号时,两者的频域互相关结果的峰值位置处于非0偏移频点,虽然相邻时隙信号均是无人机遥控器信号,但不属于同一跳无人机遥控器信号。

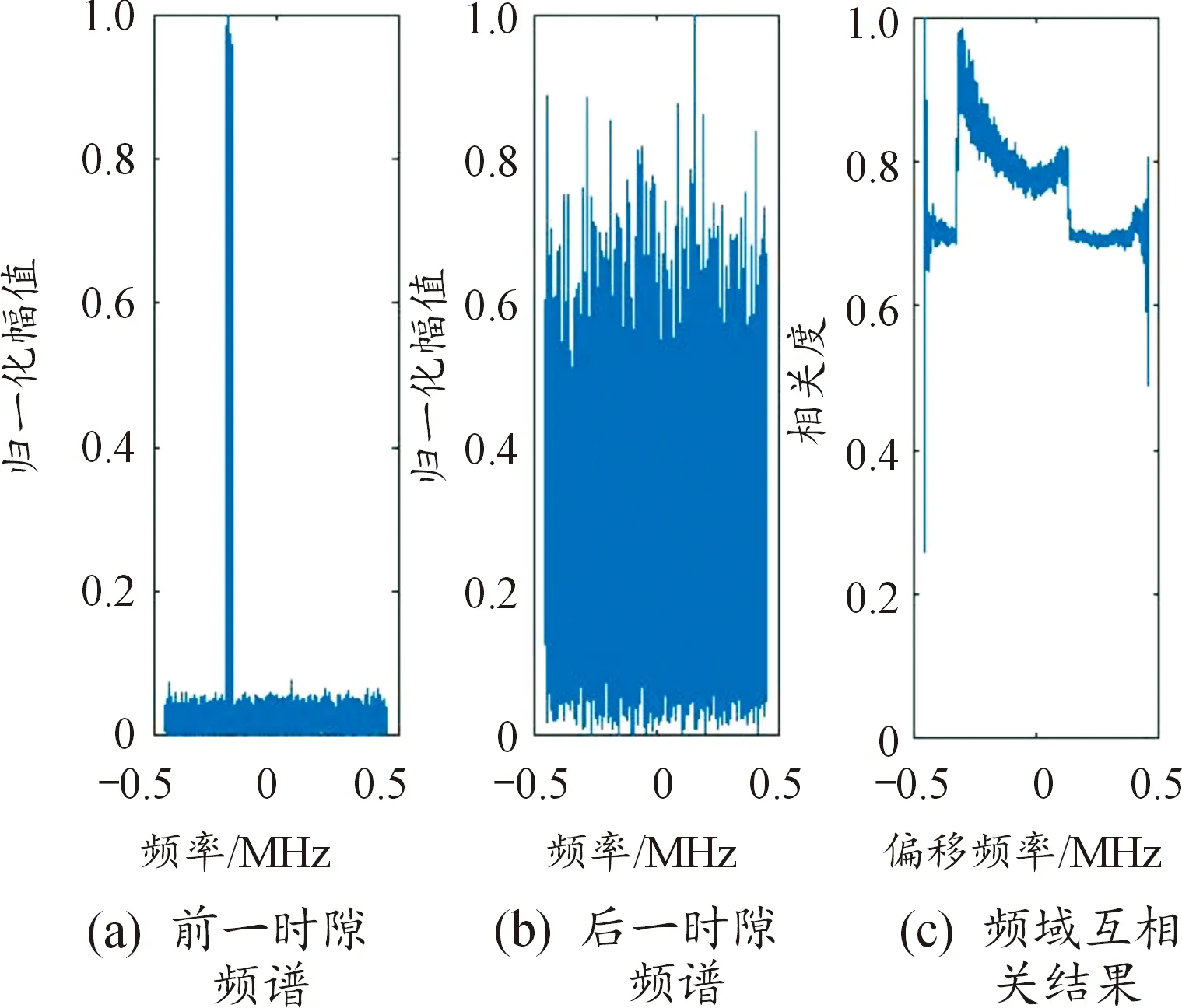
图1 跳频信号与噪声的计算结果Fig.1 The calculation results of frequency hopping signal and noise

图2 相邻跳的跳频信号计算结果Fig.2 The calculation result of adjacent hops of frequency hopping

从图3的结果可以看到当相邻时隙信号的前一时隙和后一时隙属于同一跳信号相邻时隙时,两者的频域互相关结果峰值处于0偏移频点附近。

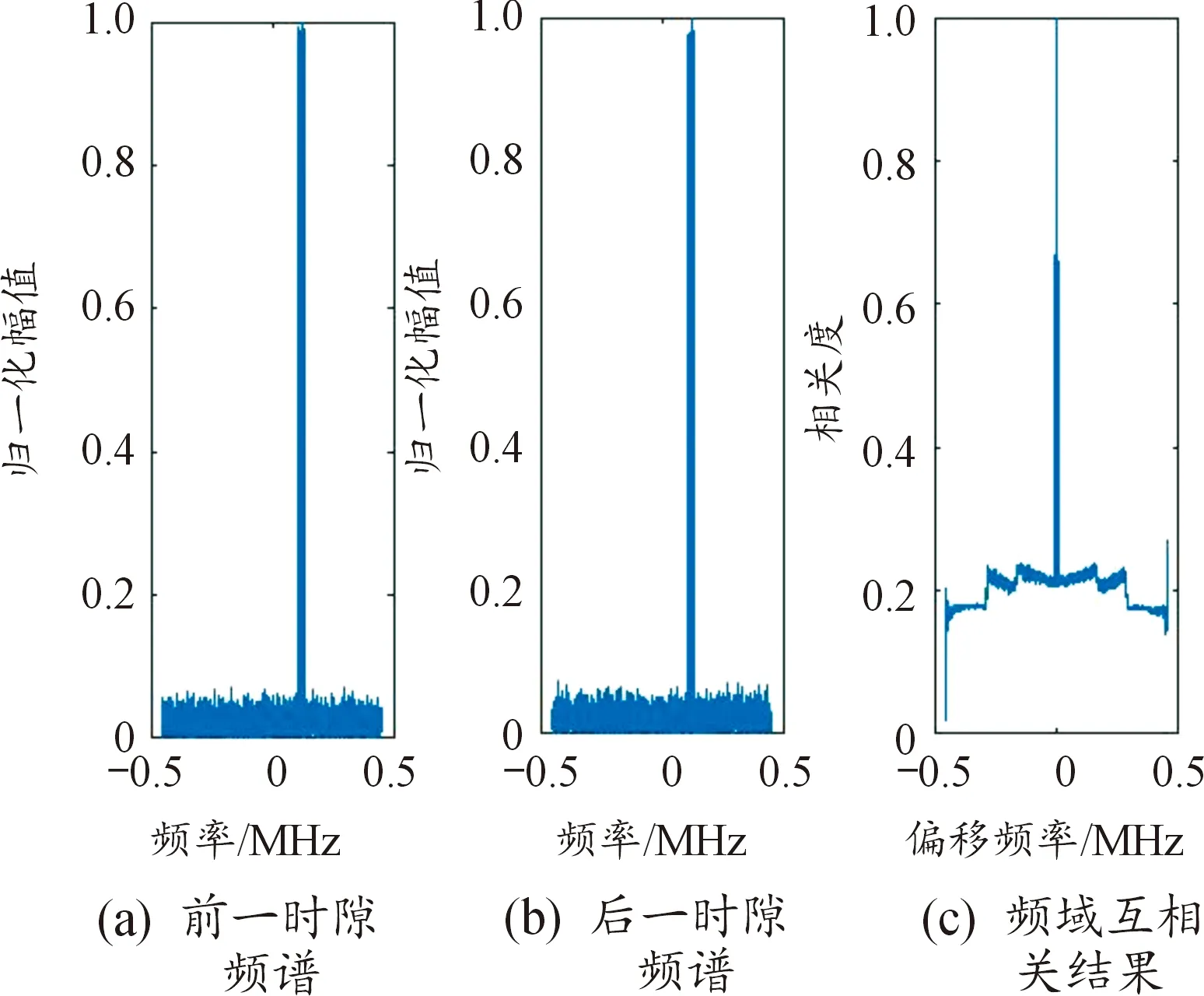
图3 同一跳的跳频信号计算结果Fig.3 The calculation result of the same hops of frequency hopping

基于此,本文中引入逻辑回归算法对相邻时隙信号的频域互相关结果进行二分类,判断相邻时隙信号是否为同一跳信号从而估计出无人机跳频信号的起跳时刻、每跳驻留时长等特征参数。然后根据这类特征参数以跳为单位分割信号并对每跳信号进行傅里叶变换,利用门限自适应去噪算法在频域上对每一跳信号进行去噪处理,最后计算最大频点值和最小频点值的差值、均值得到每跳信号的带宽、中心频率。首先按如下步骤训练逻辑回归分类器。

1) 把信号划分时隙转换为单个时隙样本点数L,并将信号g(n)划分为N/L段,得到:

gm=[g((m-1)L+1),g((m-1)L+2),…,g(mL)],

m=1,2,…,N/L

(7)

2) 求每一时隙信号gm的傅里叶变换得到Gm并计算相邻时隙信号的频域互相关结果:

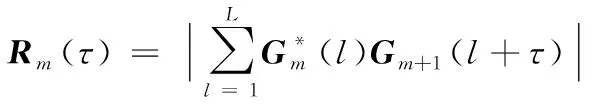
(8)

3) 生成训练集。频域互相关结果峰值处于零点位置附近的样本设标签为‘1’,否则设标签为‘0’。

4) 将训练集送入逻辑回归分类器,经过训练、迭代得到已训练的分类器model。

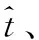
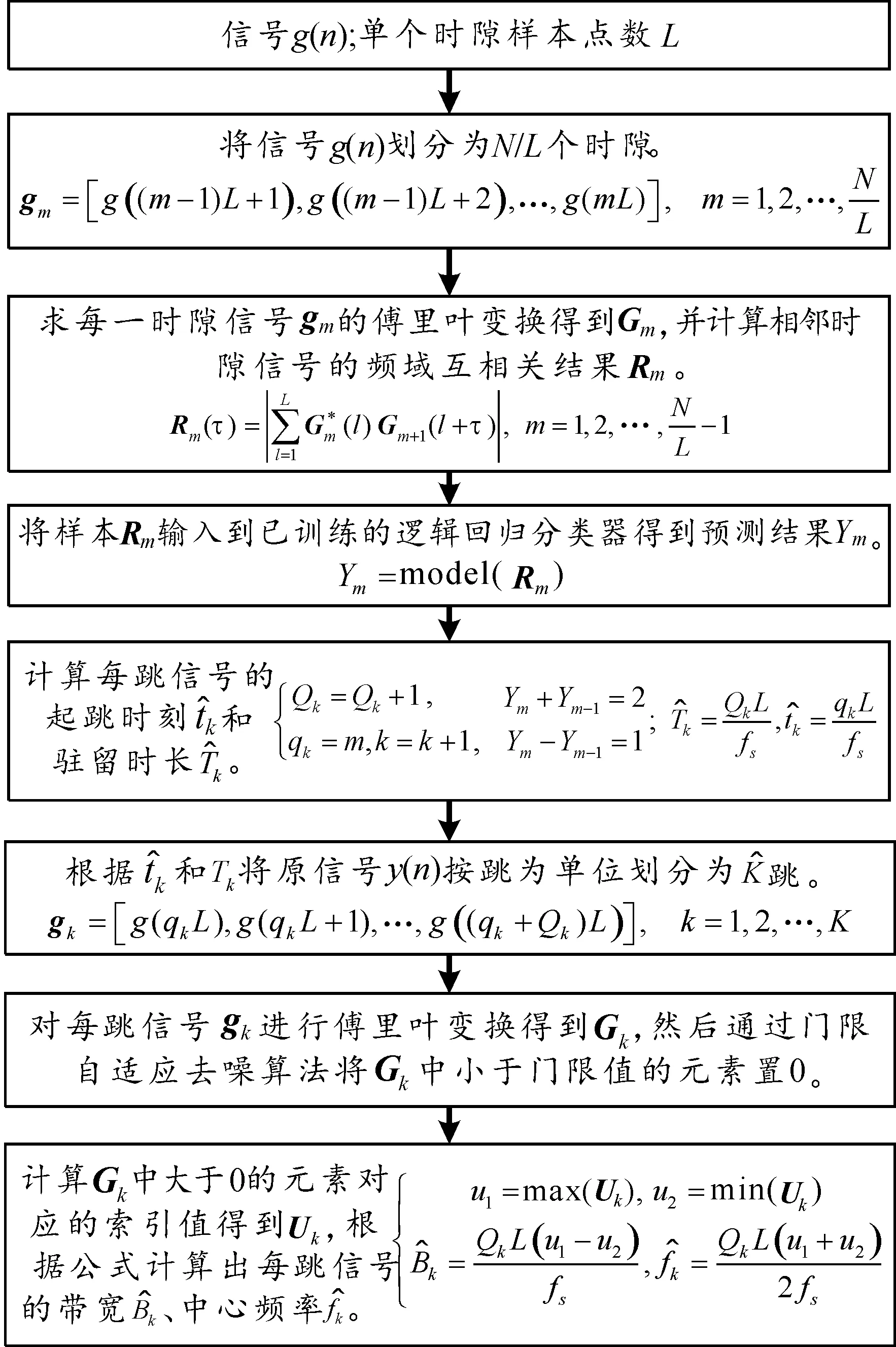
图4 无人机遥控器信号参数估计流程图Fig.4 The parameter estimation flowchart of the signal of UAV remote controller

值得注意的是,相同跳信号内的相邻时隙信号具有较强的频域互相关性,同时逻辑回归算法在分类任务中具有运算速度快和准确度高的特点。因此在满足相邻时隙信号的频域互相关这一前提下,单个时隙样本点数L越小,所提方法对每跳信号的起跳时刻、驻留时长参数的估计就越准确,且所提方法能同时兼顾时间、频率分辨力。

3 仿真实验与分析

3.1 评价指标

为验证所提方法的跳频信号参数估计性能,引入基于时频脊线的跳频参数估计法、基于最大值图的跳频参数估计法作为对比方法1、对比方法2。同时,使用平均相对误差(mean relative error,MRE)作为每跳驻留时长参数估计性能的评价指标:

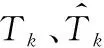
使用均方根误差(root mean square error,RMSE)评价起跳时刻、每跳中心频率估计性能:

(10)

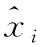
3.2 仿真实验

通过仿真实验对比分析小型无人机信号被完整采集时所提方法与传统方法的参数估计性能。仿真场景:跳频信号的频率变化范围为10～250 kHz,频率间隔为50 kHz,每跳信号驻留时长为10 ms,采样率为900 kHz,采样时间为0.5 s。对信号加注信噪比变化范围为-10～8 dB,步长为2 dB的高斯白噪声,在每个信噪比场景下进行1 000次蒙特卡洛仿真实验。

图5和图6的结果表明:对于每跳驻留时长和起跳时刻参数的估计:当信噪比达到2 dB时,对比方法的性能得到了小幅度的提升,误差大约保持在10-3～10-4;信噪比达到2 dB后,所提方法拥有逻辑回归算法的加持,在信噪比达到-2 dB时便得到了极大的提升并趋于稳定,误差降低到了10-6左右。

图5 每跳驻留时长估计平均相对误差Fig.5 MRE of estimated dwell time per hop

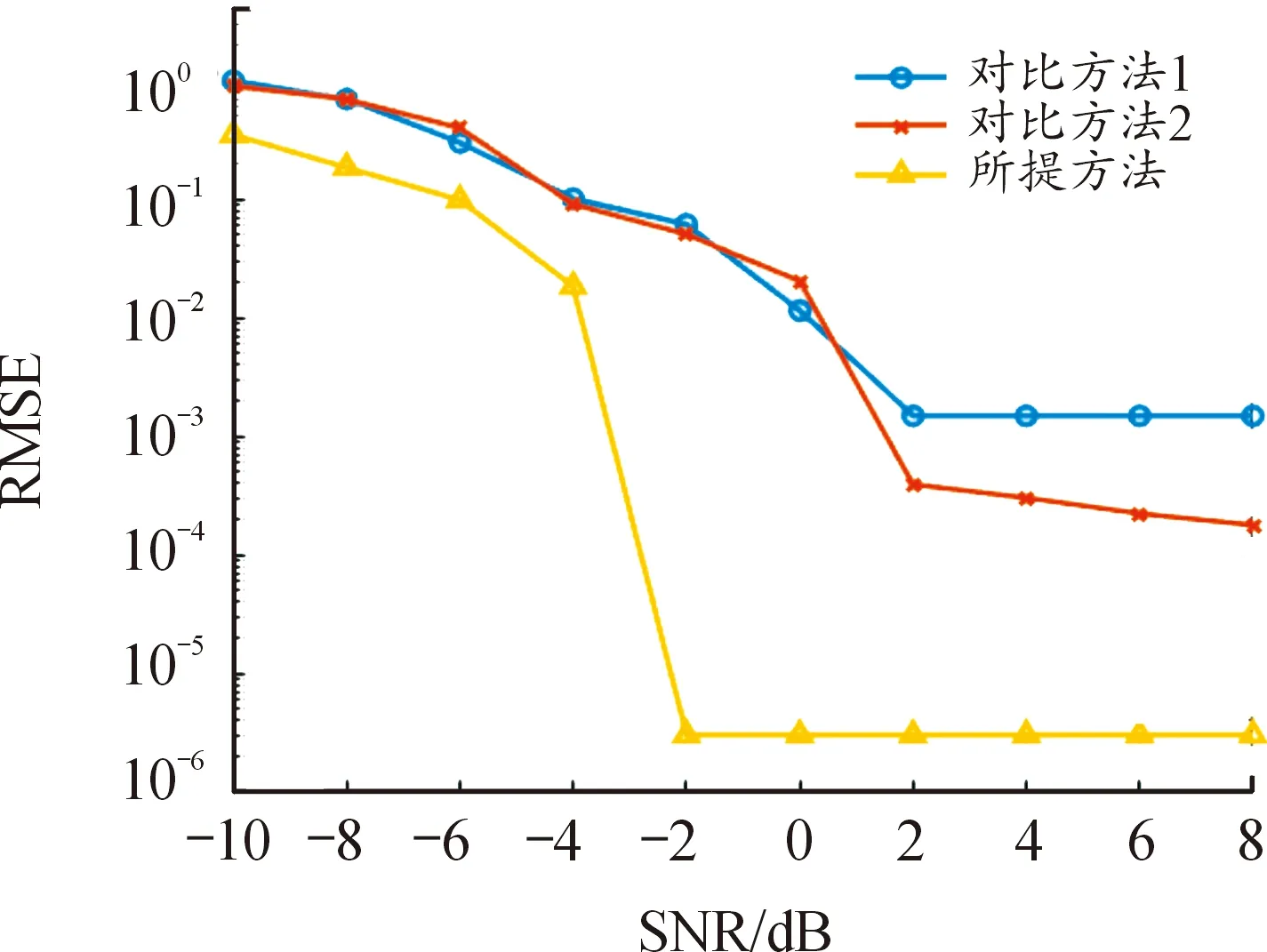
图6 每跳起跳时刻估计均方根误差Fig.6 RMSE of estimated frequency change time per hop

图7为3种方法对每跳中心频率参数估计的误差结果。由于阈值的设定,传统方法在极低信噪比下估计结果误差较大,且随着信噪比的增加参数估计性能的提升幅度较小,最小误差在5×10-1左右。而所提方法引入了门限自适应去噪算法,性能得到了大幅提升,最小误差大约为10-3。

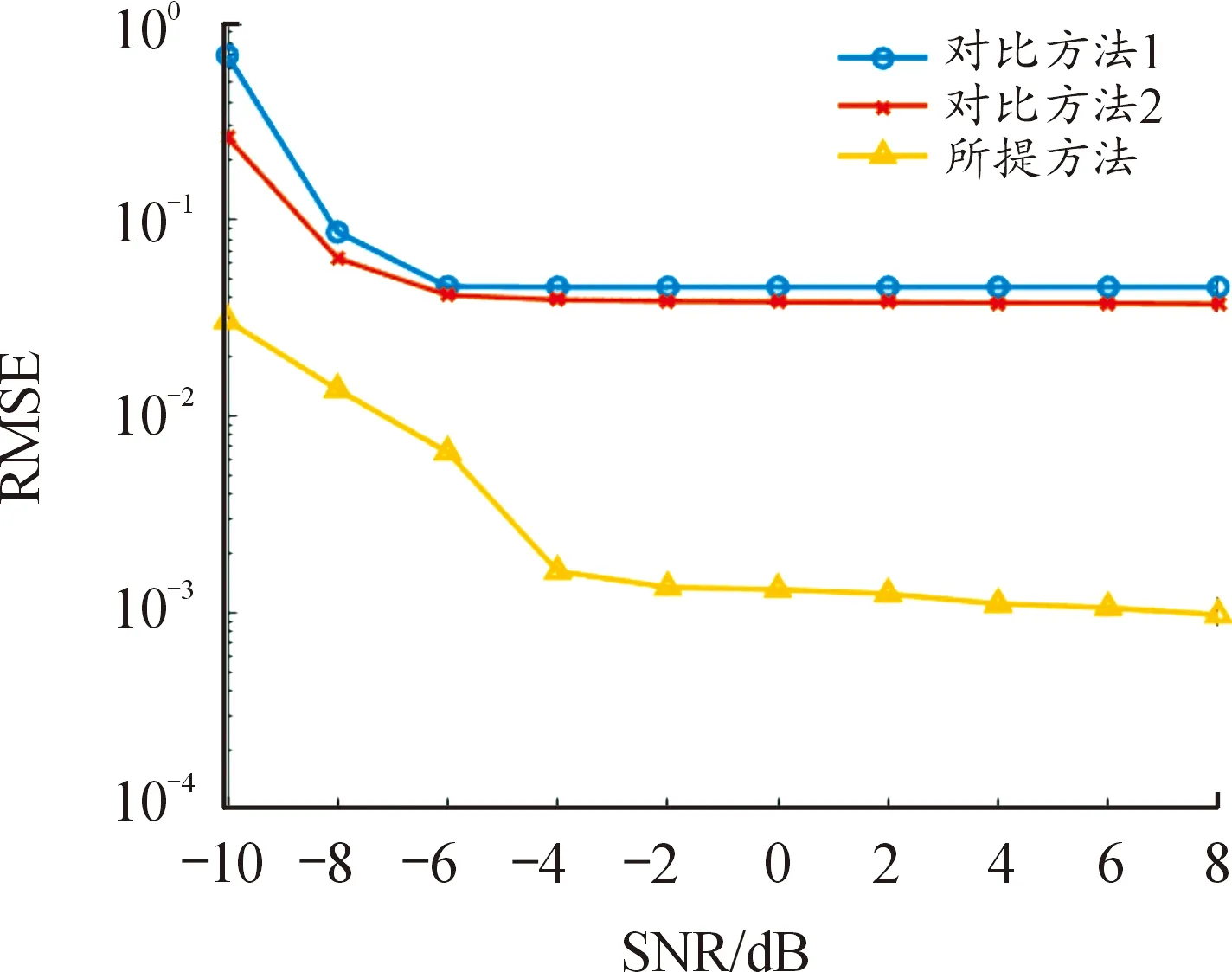
图7 每跳中心频率估计均方根误差Fig.7 RMSE of estimated instantaneous center frequencyper hop

3.3 实验分析

为验证所提方法的可行性和有效性,进一步完成对实测数据的实验分析。在微波暗室放置分布式智能频谱传感器、大疆精灵4无人机遥控器。将分布式智能频谱传感器的监听范围设置为2 410～2 420 MHz,数据采集平台采样率设置为10 MHz,采集时长为1 s。实验设备如图8所示。

图8 分布式智能频谱传感器与无人机遥控器(左)、多通道数据采集板卡(中)、数据采集平台(右)Fig.8 Distributed intelligent spectrum sensor and drone remote controller (left)、Multi-channel data acquisition board (middle)、Data collection platform(right)

信号采集设备采样率小于无人机遥控器信号的跳频总带宽时无法完整地采集无人机遥控器信号,所采集的无人机遥控器信号在时域上具有不连续性。当某一时隙信号全是噪声时,基于时频脊线的跳频参数估计法(即对比方法1)仍会将噪声频域信号的最大值对应的频率值作为跳频信号的瞬时频率,这使得该方法不再适用,因此后续实验舍弃了该方法。首先分别对接收信号的每跳驻留时长、起跳时刻、中心频率参数进行100次测量实验,并将各参数测量值的平均值作为后续实验的真实值。然后对信号加注信噪比变化范围为-12～15 dB,步长为3 dB的高斯白噪声,在每个信噪比场景下进行1 000次蒙特卡洛实验。

从图9的每跳驻留时长估计平均相对误差结果中可以得知,所提方法在信噪比极低的场景下性能优于对比方法2,并且在信噪比达到-6 dB时便得到了极大的提升并趋于稳定。图10中起跳时刻估计均方根误差结果反映出所提方法的参数估计性能全面优于对比方法2,这与仿真实验的结果一致。

图9 每跳驻留时长估计平均相对误差Fig.9 MRE of estimated dwell time per hop

图10 每跳起跳时刻估计均方根误差Fig.10 RMSE of estimated frequency change time per hop

图11为每跳中心频率参数估计均方根误差结果,在信噪比极低的场景下噪声与信号的功率差异非常细微,无法通过门限值去除噪声。但当信噪比达到-6 dB,噪声与信号的功率差异逐步增大,门限自适应去噪算法能有效去除噪声,提高参数估计性能。同时当信噪比大于-3 dB后,所提方法的参数估计性能趋于稳定且对噪声的敏感度极低。

图11 每跳中心频率估计均方根误差Fig.11 RMSE of estimated instantaneous center frequencyper hop

4 结论

通过引入逻辑回归、门限自适应去噪算法提出了一种适用于估计时域连续和时域非连续跳频信号参数的方法。并将该方法在仿真实验和实测实验中进行性能测试,得到以下结论:

1) 当信噪比达到-3 dB后,相邻时隙信号的频域互相关性逐渐提高,逻辑回归算法能准确地判断相邻时隙信号是否属于同一跳信号,因此所提方法对驻留时长、起跳时刻参数估计性能得到大幅提升。

2) 所提方法利用门限自适应去噪算法去除噪声,然后估计出每跳信号的中心频率。在信噪比达到-3 dB时对该参数的估计性能达到饱和,均方根误差达到了10-2。

3) 在噪声干扰下,所提方法的参数估计性能全面领先于传统的时频分析法。