公司股票对数收益率的分析与预测
——以T能源公司为例
2023-05-03程瀚哲首都经济贸易大学
程瀚哲 首都经济贸易大学
股票是现代金融市场中最常见、最重要的金融工具。股票市场在市场经济活动中起到了至关重要的作用。股票市场可以让企业发行股票筹集生产资本。企业可以通过股市传播企业信息以起到宣传作用、能够反映企业自身的真实运营状况及优化经济市场资源配置。对于投资者来说,股票市场有了更多的投资原则,扩大了投资的选择范围,股票市场上可以随时进行股票交易也降低了投资者投资所需要承担的风险。对于国家来说,股票市场一直都是市场经济的晴雨表,此外很重要的是能使社会的闲散资金合理流动。而没有股票市场,常规的商品交易很难像股市一样集成全国乃至全球范围的,因为其虚拟资本运作的形式而摆脱了地域的限制来统合整体的经济活动[1]。
股票市场的研究和预测难度很大,因为影响股票市场的因素众多,国家政策、企业发展、投资情绪以及普遍存在大量的随机事件导致股票市场变幻莫测,从因素上对股市进行分析很难有准确的预测。因此时间序列模型往往是用来进行股票价格预测的普遍选项。时间序列分析是通过数据本身的变化来反应数据走向规律的一种数据分析模型,常用的模型包括自回归AR模型、移动平均MA模型、自回归移动平均ARMA模型、差分自回归移动平均ARIMA模型、自回归条件异方差ARCH模型、广义自回归条件异方差GARCH模型等。应用合适的模型是时间序列分析的重要步骤之一,将股票数据拟合为恰当的模型能够给股票价格带来有价值的预测结果。
一、数据背景
本文所使用的数据集是来源于Kaggle平台的公开数据集:https://www.kaggle.com/rpaguirre/tesla-stockprice。该数据集记录了T公司从2010年6月29日到2017年3月17日每天的股票价格数据。本文选取其中的收盘价序列(Close)进行分析,计算其更具研究意义的对数收益率,并对此对数收益率序列进行时间序列建模和预测。
二、收盘价序列的描述性分析
首先,绘制出每日收盘价序列的时序图(见图1)。
从收盘价序列时序图中可以看出,数据总体呈现出上升趋势,并且具有随着股价增加波动幅度更大的迹象,该序列的标准差近似与其水平值成正比。因此,本文根据此特征,需对此收盘价序列进行对数变换,以调整该序列的方差至近似一致。
然后,绘制出对数收盘价序列的时序图及其延迟100阶的样本自相关图(见图2)。

图2 对数收盘价序列时序图
经观察,对数变换后的收盘价序列在方差一致性方面确实有了显著的改善。此外,对数收盘价序列仍具有明显的上升趋势,且不具有短期相关性。因此,本文认为此序列非平稳,对于其是否为差分非平稳,还需做单位根检验来进行进一步的探究。
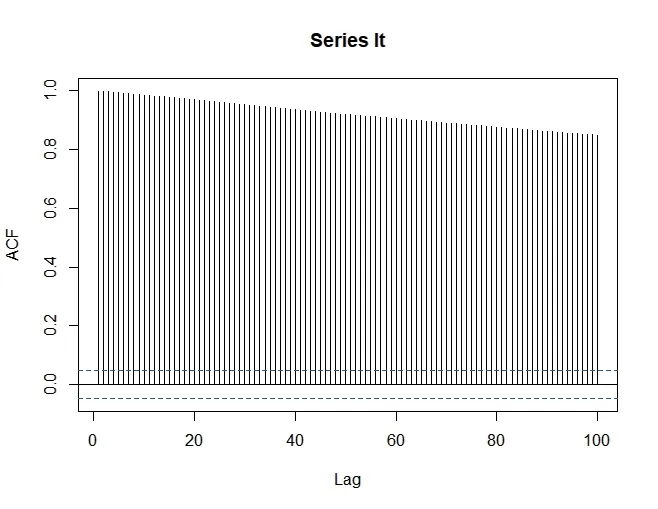
图3:对数收盘价序列ACF图
三、模型识别
(一)ADF检验
对上述对数收盘价序列做一阶差分,记差分后的数据为对数收益率,接下来,根据对数收益率序列的样本偏自相关函数图和R语言中的ar函数选择ADF检验时自回归模型的阶数,对数收益率序列拟合自回归模型时AR项阶数选择为0,于是ADF检验就退化为DF检验,对数收盘价序列DF检验结果如下:

表1 ar函数对对数收益率序列的估计结果
由于p值大于0.05,于是在0.05的显著性水平下不拒绝原假设,即认为对数收盘价序列单位根非平稳。
进而需要检验对数收益率序列是否单位根非平稳(步骤同上述DF检验):

表2 ar函数对对数收益率一次差分序列的估计结果
由于p值小于0.05,于是在0.05的显著性水平下拒绝原假设,即认为对数收益率序列平稳,因此不需要对对数收盘价序列做二次差分。
综上,对数收盘价序列非平稳。若想实现平稳,则应对此序列进行一次差分处理,形成对数收益率序列。
(二)对数收益率序列的描述性分析
首先,计算对数收益率序列的描述统计量。
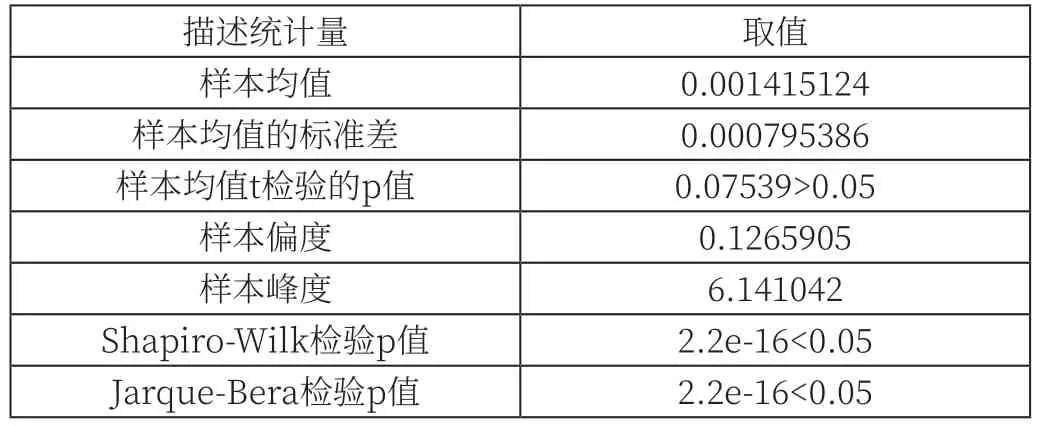
表3 对数收益率序列的描述统计量
由样本均值的t检验结果知:对数收益率序列的总体均值并没有显著地不同于0;正态性检验的结果显示此序列并不服从于正态分布;样本偏度为正,说明此序列右偏。
绘制对数收益率序列的样本自相关函数图,结合对数收益率序列的样本ACF图和PACF图,以及其总体均值不显著的特征,初步认定此序列为白噪声序列,接下来需进一步做Box检验,检验结果p为0.4198。
由于p值显著大于显著性水平0.05,所以该序列不能拒绝白噪声的原假设。
(三)ARCH效应检验
ARCH模型是自回归条件异方差模型,解决了传统计量经济学时间序列变量的第二个假设方差恒定所引起的问题,应用于波动性有关的广泛的研究领域,可以用来预测股票的波动率,来对风险进行控制,等等。不同于大部分预测被解释变量期望着的模型,ARCH模型能预测被解释变量的方差,准确地模拟时间序列变量波动性的变化。ARCH模型主要解释序列中明显的变化是否具有规律,说明这种变化依存的是内在传导而不是外生性结构变化,能够提高预测精度[2]。
绘制对数收益率绝对值序列的样本自相关图,并对其进行白噪声检验。检验结论为对数收益率绝对值序列存在序列自相关。白噪声检验结果也表明绝对值变换后的序列为非白噪声序列。
绘制对数收益率平方序列的样本自相关图,并对其进行白噪声检验。
对数收益率平方序列存在序列自相关,白噪声检验结果也表明平方变换后的序列为非白噪声序列。
非线性变换后不是独立的,说明原序列也是非独立的,因此,对数收益率序列具有某种自相关性,而且这种自相关性会造成序列的条件异方差性。基于此观点,需对对数收益率序列进一步做ARCH效应检验。
对此对数收益率序列做McLeod-Li检验,McLeod-Li检验在5%的显著性水平下都显著,给数据具有ARCH特征提供了强有力的证据。
对对数收益率序列做拉格朗日乘子检验,LM检验在5%的显著性水平下都显著,给数据具有ARCH特征提供了强有力的证据。
(四)GARCH模型定阶
Bollerslve在Engle的基础上,借助自回归移动平均ARMA模型的建立,建立了广义自回归条件异方差GARCH模型。他弥补了ARCH(q)模型中阶数q过大时需要过多的参数的缺陷。这是一种允许异方差中同时存在自回归项和滑动平均项的模型,GARCH(p,q)模型。显然,如果p=0时,GARCH(0,q)模型就是ARCH(q)模型,可以将GARCH模型看成是ARCH模型的推广,或者将ARCH模型看作是GARCH模型的特殊情形。
由于对数收益率序列ARCH效应的存在,所以应对此序列拟合ARCH模型或GARCH模型,首先需确定模型的阶数。
根据ARCH模型定阶应用平方序列的样本偏自相关函数图和GARCH模型定阶应用平方序列的样本EACF图所示结果,建议设定ARCH(2)模型或GARCH(1,1)模型。
四、参数估计
(一)ARCH(2)模型的估计(应用正态分布的新息)
对数收益率应用正态分布的新息建立ARCH(2)模型,记作m1,对m1模型进行参数估计。
此模型的各参数估计值都显著,模型表达式为:
检验结果显示:均值方程和波动率方程都充分拟合了数据,模型AIC为-4.05562,但标准化残差并不满足正态性假定。
(二)ARCH(2)模型的估计(应用学生t分布的新息)
对数收益率应用学生t分布的新息建立ARCH(2)模型,记作m2,对m2模型进行参数估计。
此模型的各参数估计值都显著,模型表达式为:
检验结果显示:均值方程和波动率方程都充分拟合了数据,模型AIC为-4.232647。
(三)GARCH(1,1)模型的估计(应用正态分布的新息)
对数收益率应用正态分布的新息建立GARCH(1,1)模型,记作m3,对m3模型进行参数估计。
此模型的各参数估计值都显著,模型表达式为:
检验结果显示:均值方程和波动率方程都充分拟合了数据,模型AIC为-4.061315,但标准化残差并不满足正态性假定。
(四)GARCH(1,1)模型的估计(应用学生t分布的新息)
对数收益率应用正态分布的新息建立GARCH(1,1)模型,记作m4,对m4模型进行参数估计。
此模型的各参数估计值除omega外都显著,但考虑到条件方差的长期水平不能为0,于是参数omega不予剔除。模型表达式为:
检验结果显示:均值方程和波动率方程都充分拟合了数据,模型AIC为-4.254761。
(五)模型比较
汇总上述通过检验的模型的AIC值,并进行样本内比较:

表4 模型AIC值汇总
m4模型的AIC值最小,因此,认为m4模型为相对最优模型。
五、模型诊断
画出对数收益率m4模型的波动率图像(见图4)。
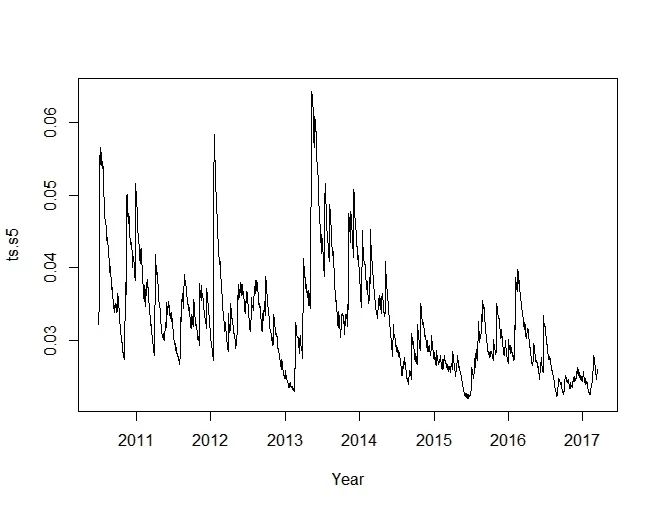
图4 m4模型的波动率图像
画出对数收益率m4模型的标准化残差时序图(见图5)。
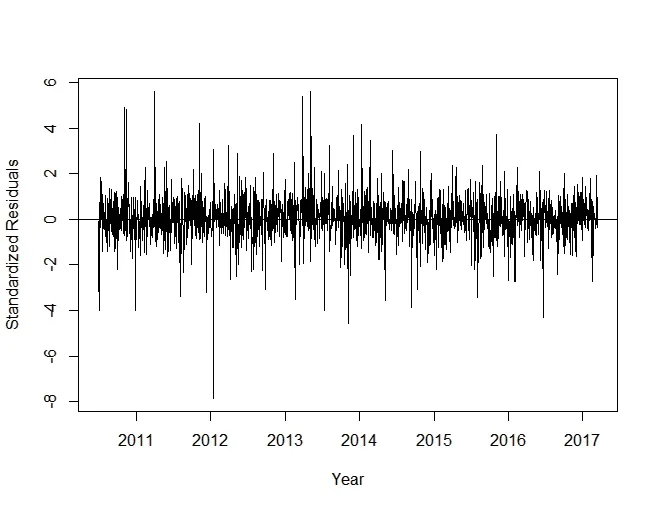
图5 m4模型的标准化残差时序图
由上图可见,标准化残差序列基本在水平线0的上下波动,且波动幅度近似一致。
画出对数收益率的m4模型的标准化残差样本自相关图(见图6)。

图6 m4模型的标准化残差样本ACF图
画出对数收益率m4模型的标准化残差平方样本自相关图(见图7)。
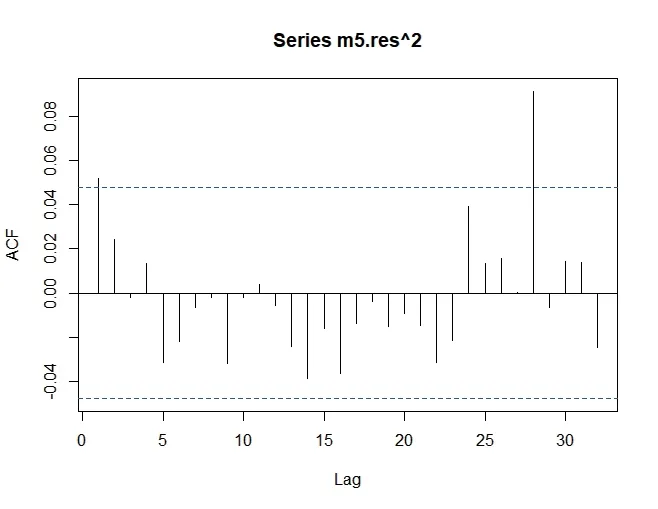
图7 m4模型的标准化残差平方样本ACF图
图6不表明标准化残差过程中有显著的序列相关性,图7不表明标准化残差过程中有显著的条件异方差性,因此,m4模型通过了诊断,可以用作预测。
六、模型预测
应用m4模型对T公司的对数收益率序列进行了10期外推预测,预测结果如下:
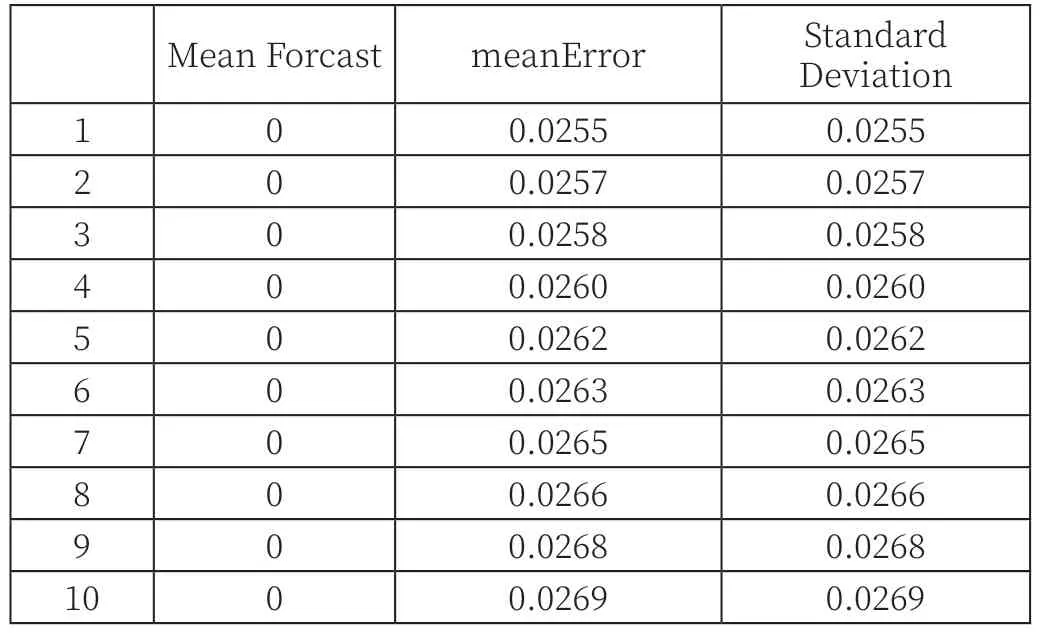
表5 对数收益率的m4模型的预测结果
保留原对数收益率序列的后50条数据,并结合上述m4模型的预测结果,绘制出如下预测图像(见图8)。

图8 对数收益率的m4模型的预测图像
