遗传蚁群混合算法在高职院校排课系统中的应用

李印坤?任宣宇

摘要：排课是高职院校的日常工作，排课管理是否合理，直接影响了高职院校的办学质量。基于此，将遗传蚁群混合算法作为研究工具，针对高职院校排课管理系统进行优化研究。将混合遗传蚂蚁算法应用于高职院校排课系统中，利用交叉函数设计和构建了高校自动排课系统。选择某高职院校的课程调度系统进行研究，利用遗传蚂蚁混合算法对原系统A进行改进，形成一个新的系统B，比较两个系统的运行时间和系统适应性。实验结果表明，系统B的适应度优于系统A，遗传蚁群混合算法可以提高课程的合理性。

关键词：遗传蚁群混合算法；排课系统；高职院校

一、前言

近年来，随着我国高职院校规模迅速扩大，许多高职院校都面临着课堂资源和教师资源不足的问题，组织课程的方式越来越难以满足不断变化的需求。排课问题一直困扰着很多高职院校，特别是班级较多而教学资源紧张的学校，每次排课都是困难重重，在实际工作中，许多学校只能无奈地选择手工排课。实现全自动化的排课系统是众多高职院校的共同期待。

排课问题是NP中的时间表问题，也就是在资源条件有限的情况下，将事件安排到适合的时间段。问题的核心在于为学院计划制定合理的课程安排，包括分配教室、时间和教师资源，并确定适当的教学时段和场地，以便有序地进行教学工作，进而设计一个满足多约束条件且高效运行的智能排课系统[1]。

国外学者解决排课问题大多采用智能算法，比如IA Ashari采用结合遗传算法和蚁群算法，以优化解决排课问题。经过实验和大量测试，证明遗传算法在此问题中表现良好[2]。G. Kendall及其团队将禁忌搜索算法与模拟退火算法相结合，提高可行解质量，并成功求解排课问题[3]。Saptarini等学者应用遗传算法有效地避免了违反硬约束条件，在最大限度上满足软约束条件[4]。C.Akka等研究人员将遗传算法和模拟退火算法相结合，适应排课规模的变化，并应用于排课系统中[5]。

但国外的排课系统普遍不适用于我国高校。袁俊毅设计了一种基于遗传算法的排课系统，成功应用于高职院校，显著提升了排课效率[6]。罗义强等学者采用改进的粒子群算法优化高校排课问题，通过该算法得到潜在解并验证其有效性。冯月华则运用动态调整信息素策略改进蚁群算法，并将其应用于排课系统中，成功缩短了排课时间。

为了提高高职院校的排课效率，本文提出一种将遗传算法与蚁群算法混合使用的方法，通过遗传算法对初始种群进行优化选择，进而生成蚁群算法所需的信息素，再通过蚁群算法求得全局最优解。本文选择某高职院校的一个教务管理系统进行实验研究，将原有的系统与运用混合算法改进后的系统进行比较，通过比较遗传蚁群混合算法的运算时间和适用性，发现该算法可以更好地提高高职院校排课的合理性。

二、高职院校的排课特点

根据教育分类的观点，高职教育不属于普通高等教育，而是技术与职业教育中的高等教育。2022年修订的新《中华人民共和国职业教育法》第三条阐明“职业教育是与普通教育具有同等重要地位的教育类型”。特殊的教育类型决定高职院校的排课工作也具有挑战性，既有普通高等学校排课的复杂性，又有自身的特殊性。

1.高职院校的特点之一是教学资源比较紧张，除了一般的教室、机房、实训室、体育场地，教师资源紧张也是高职院校在排课方面遇到困难的共同点，很多高职院校的教师周课时为18节至20节。

2.一般全院的课程表就是公共基础课的安排，专业课程由各系安排。排课中最大的挑战在于公共选修课。不同专业或班级的学生可能会选择相同的课程，而各门选修课人数也参差不齐，因此安排教室变得十分困难。

3.受到教师资源限制，很多高职院校采用两个及两个以上的班级合堂上课，需要使用合堂教室或阶梯教室，而合堂教室或阶梯教室需求量较大又会带来诸多相关的问题。

4.部分高职院校采取单双周上课模式，或者分阶段安排实训课，课程表的分阶段变化在一定程度上增加了排课的复杂性。

三、高职院校排课问题分析

基于高职院校的排课特点，排课问题主要涉及课程、班级、教师、教室、上课时间等因素，排课的实质是课程表中不能在上面5个因素之间发生冲突。为描述问题方面，下面使用5个集合表示这些因素。

（一）硬约束条件

在高职院校排课过程中，硬约束条件是必须遵守的限制条件。如果硬约束条件无法满足，则无法得到最优解，进而导致教学计划无法实施。根据高职院校的排课特点，具体硬约束条件有以下几点：

（二）软约束条件

软约束条件是指那些是否满足都不影响教学计划实施，但影响师生体验的约束条件。为了提高师生对课表的满意度，在排课的同时要充分考虑人体生物规律。在排课的过程中，满足软约束条件越多，教学计划实施起来越顺利，课表也越能让师生满意。

例如：①尽量将难度较大的课程或对思维训练要求较高的课程安排在上午第1、2节课等节次，在这些时间段学生思维相对更活跃；②体育与健康课程尽量安排在上午的第3、4节和下午的第5、6节，充分考虑到体育锻炼后因身体疲惫，不适宜立刻进入专业性过强的课程。

四、遗传蚁群混合算法

（一）遗传蚁群混合算法的基本思想

通过对参考文献的研究发现，在解决高校排课问题时，遗传算法和蚁群算法各自具有一定的优势，但也存在相应的缺陷。例如，在寻求最优解的初始阶段，遗传算法的搜索效率较高，适用于大范围的搜索。但在寻求最优解的后半阶段，遗传算法没有充分利用反馈信息，这一不足之处就会显现出来，并消耗大量的时间在无效的迭代上。突出的并行计算能力和整体优化能力是蚁群算法的最大优势，但不足之处是，在算法初期，信息素的匮乏会导致寻求最优解的速度过慢，因而该算法的运行时间比较长。

针对高职院校的排课特点，本文在前人研究的基础上进一步将遗传算法和蚁群算法结合起来使用，可以更好地发挥它们各自的优势。具体而言，在算法运行过程中，可以先充分利用遗传算法的优点，以期达到更高的搜索效率。即在初始阶段具有高效搜索的特点，进而能够生成必要的信息素，以供接下来蚁群算法的使用，然后利用蚁群算法求得全局最优解，充分利用了蚁群算法的整体优化能力和突出的并行计算的能力。

（二）遗传蚁群混合算法的执行步骤

遗传蚁群混合算法的执行步骤如下：

Step 1 初始化遗传算法的参数，生成初始种群，并将初始迭代次数设为0；

Step 2 计算所有个体的适应度函数；

Step 3 对个体进行基本遗传操作，迭代次数加1；

Step 4判断是否满足终止条件，如果满足，继续执行，否则跳至Step 2；

Step 5 利用遗传算法寻求近似最优解，并将其转化为初始信息素，以供蚁群算法使用，然后构建排课问题的二分图模型；

Step 6 在蚁群算法运行前，初始化相关参数，并将迭代次数设置为gen=0；

Step 7 将m只蚂蚁放GLSC（在二分图左侧的顶点集）中，为每只蚂蚁建立禁忌表tabuk和允许RTR选择的表allowdk；

Step 8 蚂蚁k根据排课约束条件和转移概率选取转移路径；

Step 9 对m条路径进行记录，并完成迭代；

Step 10 计算m条路径的长度，并对当前最优路径值进行记录；

Step 11 对最优路径上边的信息素量进行更新，挥发其余边的信息素；

Step 12 判断是否符合终止约束条件，若符合，则终止运算，求出当前最优路径的数值，否则gen=gen+1，并返回Step 7继续新的迭代。

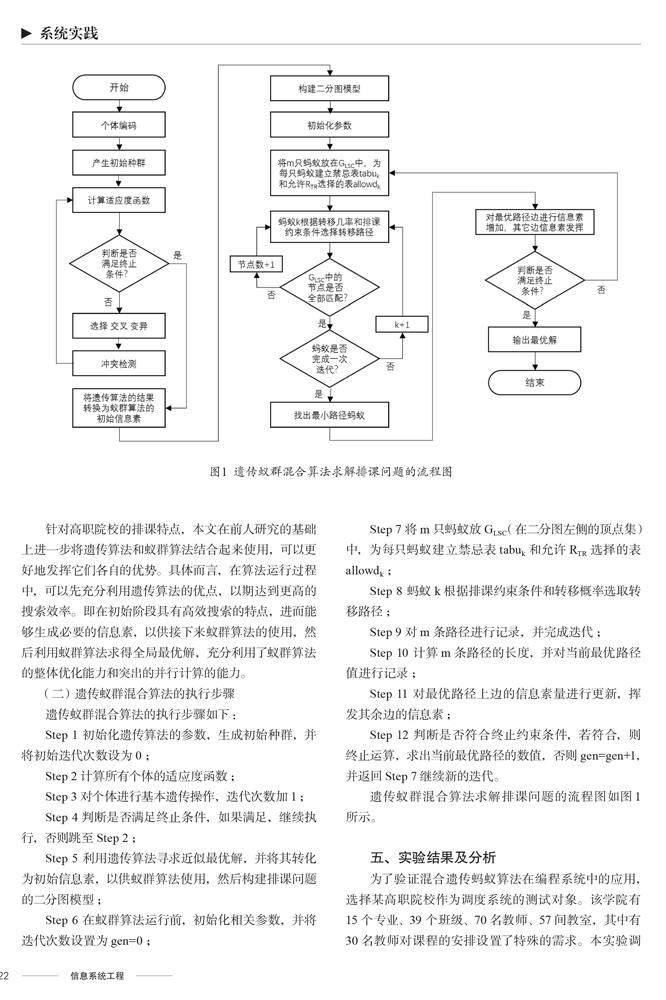
遗传蚁群混合算法求解排课问题的流程图如图1所示。

五、实验结果及分析

为了验证混合遗传蚂蚁算法在编程系统中的应用，选择某高职院校作为调度系统的测试对象。该学院有15个专业、39个班级、70名教师、57间教室，其中有30名教师对课程的安排设置了特殊的需求。本实验调度系统采用较为常用的蚁群算法，在本文研究的基础上，删除原算法，代之以遗传蚂蚁混合算法。利用上述实验数据，我们分别在蚁群算法和遗传蚁群混合算法中进行多次实验。我们将原有的蚁群算法系统简称为A系统，对于遗传蚁群混合算法则称之为B系统，并对两种算法解决排课问题的合理性、效率等方面进行验证。

（一）算法运算时间比较

当排课单元为100、400、800时，对A系统和B系统的运行时间以及适应度进行比较，并进行详细分析。算法运算时间比较如表1所示。

表1中的数据显示系统A比系统B所花费的操作时间更少。当调度单元为100时，系统A为56，系统B为36；当调度单元为400时，系统A为192，系统B为174；当调度单元为800时，系统A为578，系统B为541。

算法运算理想的时间长度是衡量算法质量的一个重要关键绩效指标。运算时间越短，可能的损失就越小，带来的机会就越多。通过表1可以发现，随着排课单元数量的增加，两种算法的运行时间也会随之增加。在排课单元数量相同的情况下，蚁群算法所需时间较长，而遗传蚁群混合算法则需要较短的时间。

（二）算法适应度比较

在遗传算法中，适应度是描述遗传算法个体性能和驱动力的主要指标。从生物学的角度来看，正常的条件相当于“适者生存”的生物可持续性竞争，这在遗传过程中很重要。建立优化问题的目标操作与个体适应性之间的映射关系，有助于实现优化问题在群体发展中的客观作用。因此，我们比较两个系统的适应性，结果如表2所示。

从表2的数据可以看出，系统B的适应性优于系统A。当调度单元为100时，系统A为191，系统B为213。当调度单元为400时，系统B比系统A高31。当调度单元为800时，系统B比系统A高69。可以看出，随着排课单元的增加，两种算法的适应度值也在增加。随着排课单元数量的增加，两种算法的适应度值都会趋于稳定。因此可以得出结论：在相同数量的排课单元下，遗传蚁群混合算法的适应度要优于单一的蚁群算法。

六、结语

综上所述，遗传蚁群混合算法的排课时间比蚁群算法短，而且其适应度值远大于蚁群算法，因此，运用遗传蚁群混合算法解决排课问题的可行性已经得到验证。将蚁群算法与遗传算法相结合，首先采用蚁群算法随机搜索，具有良好的全局收敛性，然后充分利用并行性，对前向反应机制和有效性进行了高层次的分析，建立了一种高层次分析的有效遗传算法。采用遗传蚁群混合算法可以有效提高算法的收敛速度，缩小搜索范围。实验结果表明，遗传蚁群混合算法显著提高了高职院校课程设计系统的效率和合理性。该算法生成的课程规划方案在每门课程中均匀分布，基本满足高职院校的要求。

参考文献

[1]孙弋，胡粔珲.基于遗传——蚁群混合算法的排课系统[J].计算机系统应用，2019，28（2）：81-86.

[2]Ashari IA，Muslim MA，Alamsyah A.Comparison Performance of Genetic Algorithm and Ant Colony Optimization in Course Scheduling Optimizing[J].Scientific Journal of Informatics，2016，3（2）：51-60.

[3]Goh SL，Kendall G，Sabar NR.Improved local search approaches to solve the post Enrolment course timetabling problem[J].European Journal of Operational Research，2017，261（1）：17-29.

[4]Saptarini NGAPH，Suasnawa IW，Ciptayani PI.Senior high school course scheduling using genetic algorithm[C].2018.

[5]Akkan C，Gulcu A.A bi-criteria hybrid Genetic Algorithm with robustness objective for the course timetabling problem[J].Computers & Operations Research，2018，90：22-32.

[6]袁俊毅.基于遗传算法的高校教务排课系统设计与实现[D].长沙：湖南大学，2017.

作者单位：烟台文化旅游职业学院