半休氏勒合金LiMgAs结构和热力学性质的第一性原理计算
2023-04-29杨建军逯来玉
杨建军 逯来玉

本文利用基于密度泛函理论的第一原理方法研究了Half-Heusler合金LiMgAs 的结构性质以及热力学性质. 所计算的晶格常数、弹性模量以及弹性模量对压强的导数均与实验及其他理论值相吻合. 本文还计算了α、β和γ 三种相的LiMgAs声子频率,发现没有虚频的α-LiMgAs热力学结构稳定,其他两相均有虚频,不稳定. 本文通过准谐德拜模型,研究并获得了不同温度0~1500 K和不同压强0~70 GPa下的热膨胀系数、热容、熵、德拜温度和Grüneisen参数. 我们发现,热膨胀系数、热容、熵和Grüneisen参数随温度的增加而增加,随压强的增加而减小;而温度和压强对德拜温度和弹性模量的影响和对上面其他物理量的影响恰好相反. 另外,当温度高于1000 K时,热容值变化很小,遵循Dulong-Petit定律.
第一性原理; 结构和热力学性质; 高温和高压; half-Heusler合金
O521+.2A2023.024001
收稿日期: 2022-08-05
基金项目: 国家自然科学基金(50952025); 教育部高校学生司第一期供需对接就业育人项目(202201022688)
作者简介: 杨建军(1976-), 男, 硕士, 研究方向为电子科学与技术. E-mail: jianjun.yang999@qq.com
First-principles calculations of structural and thermodynamic properties of half-Heusler alloy LiMgAs
YANG Jian-Jun1, LU Lai-Yu2
(1. Department of Microelectronics, Chengdu College of University of Electronic Science and Technology of China, Chengdu 611731, China;2. College of Physics and Electronic Engineering, Sichuan Normal University, Chengdu 610101, China)
The crystal structure and thermodynamic properties of half-Heusler alloy LiMgAs are investigated using first-principles calculations. The calculated ground-state quantities such as lattice parameter, bulk modulus and its pressure derivative are in agreement with previous works and the existing experimental data. Phonon spectra are calculated for LiMgAs in α, β and γ phases, it is found that the LiMgAs in α phase is dynamically stable due to no imaginary frequencies, the LiMgAs is dynamically unstable for β and γ phases with imaginary frequencies. Using the quasi-harmonic Debye model considering the phonon effects, the temperature and pressure dependencies of bulk modulus, heat capacity, entropy, Debye temperature, Grüneisen parameter and thermal expansion coefficient are investigated systematically in the ranges of 0~70 GPa and 0~1500 K. It is found that heat capacity, entropy, thermal expansion coefficient and Grüneisen parameter increase with the increasing temperature at a given pressure, and decrease with increasing temperature at a given temperature. However, the Debye temperature bulk modulus are contrary to the above laws of physical quantities. When temperature is higher than 1000 K, the heat capacity change a little, which obeys Dulong and Petits rule.
First-principles; Structural and thermodynamic properties; High pressure and high temperature; Half-Heusler alloy
1 Introduction
The world at present is facing two major problems relating to energy. One is the energy crisis and another is its environmental impact arising from conventional ways of utilizing energy resources. The first problem is driving research for alternative energy resources and the second problem concerns better ways of utilizing the energy resources. Thermoelectricity is considered to be one of the potential ways towards addressing both these problems[1-3]. Half-Heusler materials are considered to be potential thermoelectric materials[4-6] because of their consistent temperature stability. Furthermore, they offer the possibility of alloying, which can reduce thermal conductivity due to mass fluctuation[2]. LiMgAs is a typical Half-Heusler materials, and there are lots of studies on the material, including experimental and theoretical research[7-15].
The optical properties of LiMgAs have been measured using a photoluminescence method[7] and a scanning spectrophotometer[8]. Raman-scattering experiment has been used to measure the zone-center phonon modes of LiMgAs[9]. The structural, elastic, electronic and phonon properties of LiMgP and LiMgAs in different phases were studied by employing the plane wave pseudopotential method based on density functional theory, within the local density approximation[10]. Vibrational properties of LiMgAs in a-phase have been calculated[11] by using the density functional perturbation theory as implemented in the ABINIT code. The electronic and optical properties of the filled tetrahedral compounds LiMgN, LiMgP and LiMgAs were carried out which based on the First principles calculations by means of the full-potential linearized augmented plane wave method within the local density approximation[12]. Covalent bonding and the nature of band gaps in some half-Heusler compounds were investigated using LAPW and LMTO calculations[13]. The half-Heusler ternary LiMgZ (Z = P, As, Bi) compositions were discussed using the first principles study in the density functional theory and FP-LAPW method to study thermoelectric behaviors, electronic structure and structural properties[14]. First-principles calculations were performed to study electronic structures and magnetic properties of Mn doped LiMgAs system[15]. Despite much work on the structural and electronic properties of LiMgAs, however, few people have investigated the thermodynamic properties under pressure and temperature. In this work, the structural and thermodynamic properties for LiMgAs are researched using first principle within a generalized gradient approximation (GGA).
2 Calculation methods
The first-principles calculations of LiMgAs are performed by using CASTEP simulation package[16] which is based on density functional theory. The Vanderbilt ultrasoft pseudopotential[17] is used. Exchange-correlation effects are taken into account using the Generalized Gradient Approximation (GGA) of Perdew-Burke-Ernzerhof (PBE)[18]. The plane wave cut-off energy of 460 eV is employed. The valance electrons is considered in this study included 1s2s1 for Li, 2p63s2 for Mg and 4s24p3 for As. The k-point meshes of 4 × 4 × 4 are generated by using the Monkhorst-Pack scheme[19].
The calculations of thermodynamic properties, which are carried out by using the GIBBS program, are based on the Quasi-Harmonic Debye model (QHD)[20,21]. After the parameters of the minimum energy are calculated, the lattice parameters are obtained, the GIBBS code is input with the energy-volume (E-V) data acquired from the first-principles calculations using the previous structure set.
3 Results and discussion
3.1 Structural properties
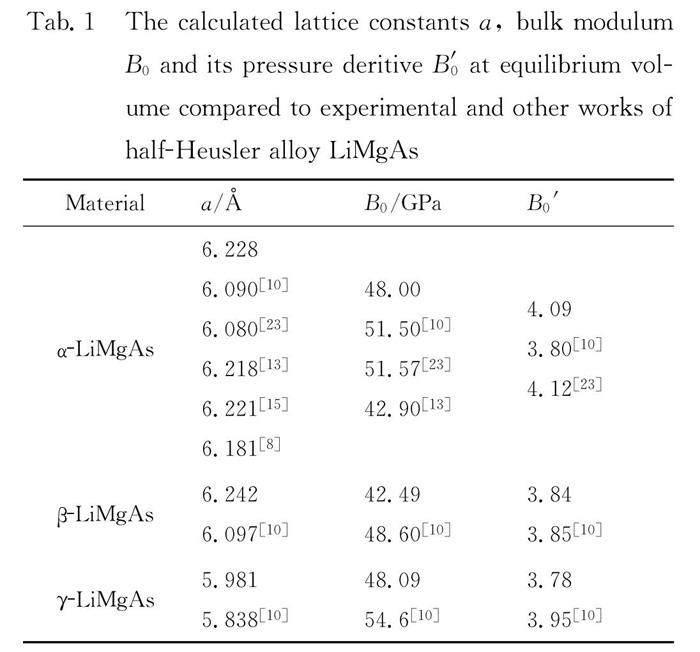
LiMgAs crystallizes in tetrahedral structure with a space group F43m. The structure can be assumed to be derived from the combination of a rock-salt type (NaCl) structure with a zinc-blende type structure. Mg cation sits at (0, 0, 0), with As at (0.25, 0.25, 0.25) and Li at (0.5, 0.5, 0.5) (α phase). It is also feasible for Li to occupy either the (0.75, 0.75, 0.75) site neighboring the Mg cation position (β phase) or switching with As sit in between the Mg and As (γ phase). For the α phase, β phase and γ phase of the LiMgAs, a series of the different lattice constant a are set to calculate the total energies E and corresponding volumes V, which shown in Fig. 1. It is noted that the α phase is the most stable state. The energy-volume(E-V) can be obtained by fitting the calculated E-V data to the third Birch-Murnaghan EOS[22]. At equilibrium volume, the obtaining lattice constants, bulk modulum B0(GPa) and its pressure deritive B′0 for the α phase, β phase and γ phase of the LiMgAs are listed in Tab. 1, compared with experimental data[8] and other theoretical results[10, 13, 15, 23]. It is seen the calculated values are in good agreement with experimental value and other calculated results.
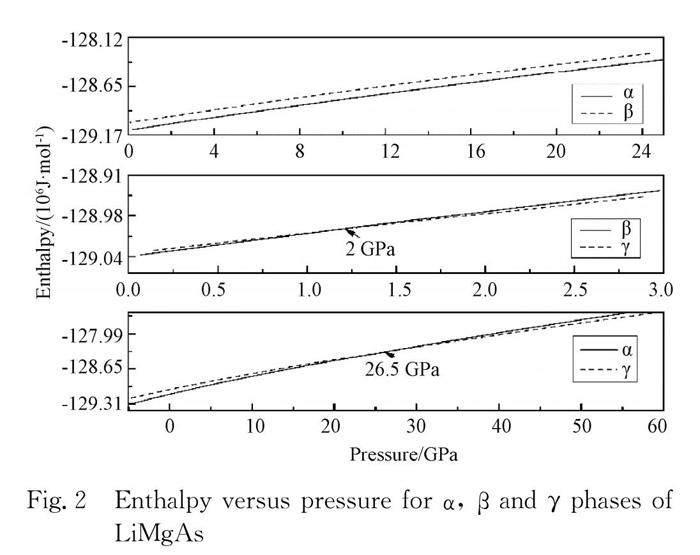
In order to investigate the behaviors of the phase transition pressure, we obtain the relation of the enthalpy and pressure using the third Birch-Murnaghan EOS[22]. According to the isoenthalpy principle, the phase transition pressure for the α phase and the γ phase is 26.5 GPa, for the β phase and the γ phase is 2 GPa, while there is no transition pressure for the α phase and the β phase, which is shown in Fig. 2.
3.2 Dynamical properties
The importance of the phonon interpretation of lattice dynamics is illustrated by the large number of physical properties that can be understood in terms of phonons: infrared, Raman, and neutron scattering spectra, specific heat, thermal expansion, and heat conduction, and so on. The basic theory of phonons, in crystals is well understood and has been described in detail[24,25]. In our phonon calculations, finite displacement calculations are carried out in the supercell with cutoff radius 5.0 , 7× 7 × 7 meshes are used in the interpolation of the phonon calculations. the phonon dispersion curves along the high symmetry directions in the Brillouin zone for LiMgAs in the α, β and γ phases are plotted in Fig.3. There are no imaginary frequencies in α phase in the Brillouin zone, however, the β phase and the γ phase have imaginary frequencies, which intimates the LiMgAs in α phase is dynamically stable, the LiMgAs is dynamically unstable for β and γ phases. So, the following thermodynamic properties will only focus on the the α phase of LiMgAs.
The calculated phonon frequencies of α phase at the zone center are TO(G)=238.82 cm-1, LO(G)=302.46 cm-1 , which agree well with the previous theoretical results[10] (TO(G)=253.30 cm-1, LO(G)=303.70 cm-1) and are smaller than experimental results (TO(G)=307 cm-1, LO(G)=329 cm-1). The discrepancies between the theoretical calculation and experimental results are similar to LiZnAs with identical structure[26], which may result from the difference between the observed and calculated lattice constants and lattice imperfection. Our calculated value of the zone-center LO(G)-TO(G) splittings are 63.64 cm-1 for the LiMgAs in α phase.
3.3 Thermodynamic properties
To investigate the thermodynamic properties of LiMgAs under high temperature and high pressure, we have applied the quasi-harmonic Debye approximation. As the first step, a set of total energy calculation versus primitive cell volume (E-V), in the static approximation, is carried out for each compound and fitted with the third Birch-Murnaghan EOS in order to determine its structural parameters at p= 0 and T = 0, and then derived the macroscopic properties as a function of p and T from standard thermodynamic relations. The thermal properties are determined in the temperature range from 0 to 1000 K, the pressure range from 0 to 70 GPa.
The bulk modulus variation versus temperature at a given pressure is showed in Tab. 2. The compressibility increases with increasing temperature at a given pressure and decreases with pressure at a given temperature. These results are due to the fact that the effect of increasing pressure on the material is the same as the decreasing temperature of the material. The effect of the temperature T on the isothermal bulk modulus is less important than that of the pressure.
The variation of the thermal expansion coefficient α as a function of temperature and pressure is showed in Fig. 4. It is shown that, at a given pressure, α increases sharply with the increase of temperature up to 300 K. When T > 300 K, α gradually increases linearly with enhanced temperature and the propensity of increment becomes moderate, which means that the temperature dependence of α is very small at high temperature. For a given temperature, α decreases drastically with the increase of pressure.
Knowledge of the heat capacity of a substance not only provides essential insight into its vibrational properties, but also is mandatory for many applications. The relationship between the heat capacity CV and temperature at different pressures (p = 0, 20, 40, 70 GPa) is shown in Fig. 5, and CV is calculated by the obtained phonon dispersion, which is plotted hollow circle in Fig. 3. It is shown that the thermodynamic properties of LiMgAs based on the quasi-harmonic Debye approximation are reasonable. CV is very small at low temperatures, and approaches a constant value at high temperatures. At low temperatures, CV increases exponentially, which follow the Debye model (CV~T3), and at sufficiently high temperatures (>1000 K), the heat capacity obeys Dulong and Petits rule, and the difference between them is very slight, which are similar to the calculational results[27-31].
Entropy is a measure of the chaos for a material system. Entropy under different pressures and temperatures is showed in Fig. 6. Under the same pressure, the entropy increases with the increase of temperature, and the increasing trend gradually slows down at high temperature. At the same temperature, entropy decreases with the increase of pressure. The rise and fall of entropy is relate to the vibration between LiMgAs atoms. Pressure reduces the vibration amplitude of Li, Mg and As atoms, so entropy decreases with increasing Pressure.
The Debye temperature θD is closely related to many physical properties of solids, such as elastic properties, sound velocities, hardness and specific heat. Another important thermodynamic parameter is Grüneisen parameter γ, which describes the anharmonic effects in the crystal vibrations, and also, it is used to characterize the thermodynamic behavior of a material at high pressures and temperatures. the Debye temperatures and Grüneisen parameters for LiMgAs at different pressures and temperatures are listed in Tab. 2. At a constant temperature, θD increases with the increasing pressure, while γ decreases. However, at a constant pressure, θD decreases with the increasing temperature, while γ increases.
4 Conclusions
Using the first-principles plane-wave pseudopotential density functional theory within GGA and the quasi-harmonic Debye model (QHD), the structural, thermodynamic properties of LiMgAs have been investigated. The calculated structural parameters at zero pressure are in agreement with the available experimental data. It is found the phase transition pressure for the α phase and the γ phase is 26.5 GPa, and for the β phase and the γ phase is 2 GPa. No phase transition occurs between α phase and β phase. There are no imaginary frequencies in the α phase, which intimates the LiMgAs is dynamically stable in α phase, and β and γ phases are unstable due to imaginary frequencies.
It is found that the high temperature leads to a smaller bulk modulus, a larger heat capacity, larger entropy, larger thermal expansion coefficient and a larger Grüneisen parameter at a given pressure. However, the high-pressure results in a larger bulk modulus, a smaller heat capacity, a smaller entropy, a smaller Grüneisen parameter and a smaller thermal expansion coefficient at a given temperature. The heat capacity and the thermal expansion coefficient tend to a constant value at high temperatures and high pressure.
References:
[1] Snyder G J, Toberer E S. Complex thermoelectric materials [J]. Nat Mater, 2008, 7: 105.
[2] Alam H, Ramakrishna S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials [J]. Nano Energy, 2013, 2: 190.
[3] Yadav M K, Sanyal B. First-principles study of thermoelectric properties of CuI [J]. Mater Res Express, 2014, 1: 015708.
[4] Hohl H, Ramirez A P, Goldmann C, et al. Efficient dopants for ZrNiSn-based thermoelectric materials [J]. Phys Condens Matter, 1999, 11: 1697.
[5] Nolas G S, Poon J, Kanatzidis M. Recent Developments in Bulk Thermoelectric Materials [J]. MRS Bulletin, 2006, 31: 199.
[6] Yu C, Zhu T J, Shi R Z, et al. High-performance half-Heusler thermoelectric materials Hf1-xZrxNiSn1-ySby prepared by levitation melting and spark plasma sinteri [J]. Acta Mater, 2009, 57: 2757.
[7] Kuriyama K, Kushida K. Band edge and phonon-assisted deep level emissions in the ordered filled tetrahedral semiconductor LiMgP [J]. J Appl Phys, 2000, 87: 2303.
[8] Kuriyama K, Kushida K. Optical band gap of the filled tetrahedral semiconductor LiMgAs [J]. J Appl Phys, 2000, 87: 3168.
[9] Kuriyama K, Yamashita Y, Suzuki Y, et al. Raman scattering from the filled tetrahedral semiconductor LiMgAs [C]//Caldas M J, Studart N. Proceedings of the 29th International Conference on the Physics of Semiconductors. Rio de Janeiro, Brazil: American Insititute of Physics, 2010.
[10] Soyalp F, Ugur G, Ugur S, et al. A first-principles study of the structural, elastic, electronic and phonon properties of LiMgP and LiMgAs in the a, b and c phases [J]. J Alloys Compd, 2013, 551: 108.
[11] Mellouki A, Bennecer B, Kalarasse F. Calculation of the vibrational properties of LiMgAs [J]. J Phys: Condens Matter, 2009, 21: 305402.
[12] Djeroud S, Kalarasse L, Bennecer B, et al. Electronic and optical properties of LiMgN, LiMgP and LiMgAs under hydrostatic pressure [J]. J Phys Chem Solids, 2009, 70: 26.
[13] Kandpal H C, Felser C, Seshadri R. Covalent bonding and the nature of band gaps in some half-Heusler compounds [J]. J Phys D: Appl Phys, 2006, 39: 776.
[14] Parsamehr S, Boochani A, Amiri M, et al. Thermodynamic phase diagram and thermoelectric properties of LiMgZ (Z = P, As, Bi): ab initio method study [J]. Philos Mag, 2020, 101: 1.
[15] Zhang H Y, Zhang C Y, Du Y Y, et al. Photoelectric properties of Mn-doped LiMgAs new diluted magnetic semiconductors [J]. J Funct Mater, 2019, 9: 09102.
[16] Segall M D, Lindan P J D, Probert M J, et al. First-principles simulation: ideas, illustrations and the CASTEP code [J]. J Phys: Condens Matter, 2002, 14: 2717.
[17] Vanderbilt D. Soft self-consisitent pseudopotentials in a generalized eigenvalue formalism [J]. Phys Rev B, 1990, 41: 7892.
[18] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple [J] Phys Rev Lett, 1996, 77: 3865.
[19] Monkhorst H J, Pack J D. Special points for Brillouin-zone integration J]. Phys Rev B, 1976, 13: 5188.
[20] Blanco M A, Francisco E, Luana V. GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model [J]. Comput Phys Comm, 2004, 158: 57.
[21] Poirer J P. Introduction to the physics of the earths interior[M]. England: Cambridge University Press, 1991.
[22] Hill R. The elastic behaviour of a crystalline aggregate [J]. Proc Phys Soc, 1952, 65: 350.
[23] Kalarasse F, Bennecer B, Mellouki A. Optical properties of the filled tetrahedral semiconductors LiMgX (X = N, P and As) [J]. J Phys: Condens Matter, 2006, 18: 7237.
[24] Born M, Huang K. Dynamical theory of crystal lattices [M]. Oxford: Oxford University Press, 1954.
[25] Ashcroft N W, Mermin N D. Solid state physics [M]. Stanford: Cengage Learning, 1976.
[26] Kuriyama K, Ishikawa T. Raman scattering from the filled tetrahedral semiconductor LiZnAs [J]. Phys Rev B, 2005, 72: 233201.
[27] Yi H X, Wang C J, Sun B, et al. First-principles study of structural, elastic, electronic, optical and thermodynamic properties of tungsten carbide at high temperature and high pressure [J]. J At Mol Phys(原子与分子物理学报), 2020, 37: 239.
[28] Lei H R, Zhang L H. High-pressure physical properties for P6m2-ReB2[J]. J Sichuan Univ: Nat Sci Ed, 2022, 59: 014004.
[29] Zheng P, Hou T P, Lin H Fu, et al. First-principles calculation of thermodynamic properties of alloy carbide Fe3Mo3C at high temperature and pressure [J]. J At Mol Phys(原子与分子物理学报), 2023, 40: 034001 (in Chinese).
[30] Liu Y K, Dong L J, Zhang Y Y, et al. First-principles calculations of the mechanical and thermodynamic properties of MAX phases Nb2SnC and Nb2SnN [J]. J At Mol Phys(原子与分子物理学报), 2022, 39: 066005 (in Chinese).
[31] Wang N, Du G S, Wang W X, et al. A first principles study on the mechanical and thermodynamic properties of MgCu4Sn-type rare earth-magnesium compounds [J]. J At Mol Phys(原子与分子物理学报), 2021, 38: 026003 (in Chinese).
