基于低增益LESO的有机废液焚烧系统控制算法研究

李艳 王鑫 胡振 戴庆瑜

摘 要：有机废液焚烧过程存在强耦合、强干扰、非线性、不确定性等问题导致以数学模型为基础的控制策略较难取得良好的控制效果.LADRC可利用LESO对以上因素进行估计并补偿，但当观测带宽受限时会导致LESO观测能力不足，从而使得控制效果不佳.针对以上问题，本文对LADRC进行改进，首先将实际系统转化为积分串联形式的理想系统，然后分别将控制信号作用于理想系统和实际系统并得出二者的输出偏差，再采用PI控制器对其进行补偿，弥补了因低增益LESO观测能力不足导致控制效果欠佳的缺陷.将改进后的LADRC应用于有机废液焚烧系统，仿真结果表明改进后的LADRC采用低增益LESO不仅能有效解决以上所描述的有机废液焚烧过程中存在的各控制难点，并且相较传统的LADRC具有更好的阶跃跟踪能力、抗干扰性和鲁棒性.

关键词：废液焚烧；LADRC控制；低增益LESO；PI补偿；蒙特卡洛实验

中图分类号：TP273

文献标志码： A

文章编号：2096-398X（2023）04-0143-08

Abstract：The organic waste liquid incineration process has problems such as strong coupling，strong interference，non-linearity，uncertainty，etc.，which makes it difficult to achieve good control effects for control strategies based on mathematical models.LADRC can use LESO to estimate and compensate for the above factors，but when the observation bandwidth is limited，it will lead to insufficient LESO observation ability，which makes the control effect poor.This article improves LADRC.First，the actual system is transformed into an ideal system in integral series，and then the control signal is applied to the ideal system and the actual system to obtain the output deviation of the two，and then the PI controller is used to compensate it，it makes up for the defect of poor control effect due to insufficient observation ability of low-gain LESO.Applying the improved LADRC to the organic waste incineration system，the simulation results show that the improved LADRC using low-gain LESO can not only effectively solve the control difficulties in the organic waste incineration process described above，but also has better step tracking ability，anti-jamming and robustness than the traditional LADRC.

Key words：waste liquid incineration；LADRC control；low gain LESO；PI compensation；monte carlo experiment

0 引言

隨着医药、化工等行业的用水量和排放量的不断增加，有机废液对环境造成的污染日益严重，因此需要将有机废液无害化处理后排放.对于浓度高、成分复杂、没有回收价值的有机废液通常采用焚烧的方法进行处理［1］.影响废液焚烧效果及焚烧过程安全的关键参数有炉膛温度、烟气含氧量及炉膛负压，而这三个变量之间存在严重的耦合.另外，废液成分会随时间变化，导致废液热值变化较大，因此废液焚烧过程具有干扰频繁、时变、非线性、不确定性等特征，从而使得以数学模型为基础的控制方法和传统PID控制均难以取得良好的控制效果.

LADRC能够将模型中未建模的部分、外部扰动和耦合视为“总扰动”，通过观测器实时对其进行观测并补偿［2，3］，可有效解决有机废液焚烧过程中存在的以上问题.但线性扩张状态观测器的观测能力会受到带宽的限制，当观测器的带宽选择较小时会出现观测准确性下降的问题［4］.高志强等在文献［5，6］中指出通过提高扩张状态观测器的带宽来解决此类问题.但在实际应用中，高带宽意味着高成本，并且高带宽会使得系统的稳定性下降，对外界干扰更为敏感，因此上述问题不能仅仅依靠提高带宽来解决.

对于带宽受限的问题，文献［7］提出改变误差估计值的增益，相当于闭环系统增加了一个一阶微分环节，减小扰动观测的相位滞后程度，提高状态观测器的实时观测能力，通过仿真验证其控制效果良好；文献［8］ 提出采用并联型 LESO 结构进行控制，以期望获得更优秀的扰动观测性能，经过仿真验证效果控制效果良好；文献［9］采用惯性环节对对象的延迟特性进行补偿，并针对自抗扰控制参数难调整的问题采用模糊规则进行调整，仿真验证具有较好的鲁棒性.

本文针对LESO带宽受限的问题，为方便工程实现，对LADRC进行改进［10］：采用低增益LESO对扰动进行观测，将忽略掉干扰的实际模型视为理想模型，使用参数相同的线性自抗扰控制器分别对理想模型和实际模型进行控制，并采用PI控制器对两者输出的偏差进行补偿.将改进后的LADRC应用于有机废液焚烧系统的控制中，通过MATLAB仿真验证其有效性.

1 焚烧过程数学模型

本研究团队面向有机废液焚烧过程采用机理法进行建模，通过实际数据的验证结果来看，所建立的数学模型能够满足控制系统设计的需要［11］.

焚烧过程传递函数矩阵的具体表达式为：

式（1）中：Tg表示炉膛温度，WO2表示烟气氧含量，Pg表示炉膛负压，Wc表示天然气流量，Wa表示送风量，Wg表示引风量，Wf表示废液流量.

式（1）中传递函数矩阵为非对角线矩阵，说明三条控制回路之间存在强耦合；其次，废液流量和成分的变化会对三者产生较大的影响，因此，焚烧过程存在强时变干扰；另外，废液焚烧过程包含一系列的物理、化学变化，整个过程存在强非线性和时变性，而且以上数学模型是忽略掉一些非线性因素而得到的，存在未建模的部分.

2 线性自抗扰控制器设计及误差分析

2.1 线性自抗扰控制器的设计

线性自抗扰控制技术将多输入多输出系统控制回路之间的耦合视为扰动，经过补偿后等效为多个单输入单输出的系统进行控制［12］.

本文以压力-引风量通道为例进行研究，根据传递函数可知此通道为二阶系统，可以用微分方程表示为：

式（5）中：z1，z2，z3分别表示输出的估计值，输出微分的估计值和“总扰动”的估计值.β01，β02，β03为LESO的增益值，可以通过调节参数改变观测器的观测能力.图1给出线性自抗扰控制器的结构图，图2给出压力-引风量通道的模拟结构图.

由式（15）可知：只有观测器带宽ωo→∞时，观测误差才会趋于零.这与工程实际应用中ωo不能够无限制增大相悖.

采用MATLAB对炉膛压力-引风量通道施加y=sint的干扰信号，分析观测器的观测能力，不同ωo的扰动观测信号如图3所示.当观测器的带宽ωo较小时，观测器会出现幅值衰减和相位滞后的问题，观测器很难跟踪到实际的扰动，而当观测器的带宽ωo取得较大值时，观测器可以取得较好的跟踪效果，甚至带宽取值足够大时，观测所得信号与实际扰动信号重合，但在初始时刻，观测误差会随着ωo的增大而增大，如图3所示.

因此，通过仿真实验也说明增益较小的扩张状态观测器所观测扰动的误差较大.

3 改进线性自抗扰控制器设计及分析

3.1 改进线性自抗扰控制器的设计

针对前文提出的传统LADRC的观测器在带宽较小时观测误差较大的问题，结合PI控制的原理，对传统LADRC控制器进行了改进，改进后的结构框图如图4所示.其中虚线框内为传统LADRC的基本结构，包含线性误差反馈控制律（LSEF）和线性扩张状态观测器（LESO）.

传统LADRC控制量u由偏差信号及其微分和扰动估计值线性组合而成，当LESO的带宽取值较小时，观测器难以准确估计扰动信号，系统难以达到所需要的控制效果.改进后的LADRC采用低增益LESO对扰动进行估计，其估计值和实际值会有偏差，即实际模型不能被等效为理想模型.当控制量均为u0时，实际模型的输出和理想模型的输出也存在偏差.本文将实际模型与理想模型的输出偏差通过PI控制器补偿到控制量u中，改善了控制效果.

3.2 改进线性自抗扰控制器的稳定性分析

根据线性自抗扰控制技术的思想，外部干扰信号、回路之间的耦合及建模过程中忽略的部分都被定义为总扰动，通过LESO和PI控制器进行补偿，那么原本多变量系统的第三条回路可以被等效为图5所示的单回路系统，因此只需对此单回路系统的稳定性进行证明.

由图6整理可得：

上述的结构变换简化了改进型LADRC的稳定性证明.根据劳斯判据可以得出系统稳定时参数的取值范围［17，18］，从理论上来讲，劳斯表中第一列系数均为正即可保证系统稳定的同时求得参数范围，而在实际中，一般情况会首先选取参数ωc和ωo，将其代入闭环特征方程，求得特征多项式，再依据劳斯表判断系统的稳定性.

4 仿真分析

式（8）和（11）提出的线性自抗扰控制器参数整定方法是针对二阶对象設计的，而文献［19］提出典型的工业控制对象都可以采用二阶线性自抗扰控制器进行控制，因此本文数学模型的前两条通道也采用二阶线性自抗扰控制器进行控制.

为验证改进后LADRC的控制性能，选取PID控制和传统的LADRC控制作为对照，其中LADRC控制与PI-LADRC控制的参数一致，根据带宽法进行整定，首先选择ωo=5ωc，此时需要调节的参数仅为ωc.逐步增大ωc，直到噪声影响难以承受导致系统输出波动时，停止调节ωc；逐步减小ωo至系统输出恢复稳定，再次调节ωc，依次循环调节，直到满足控制要求.PI-LADRC控制的PI补偿器参数按照经验法进行整定；PID控制的参数整定根据临界震荡法（Z-N法）进行整定，具体参数见表1所示.

4.1 阶跃响应及解耦效果验证

为验证三种控制方式的阶跃响应效果和解耦能力.在t=0 s、150 s和300 s时分别对温度、氧含量以及压力回路单独施加幅值为1、2、3的单位阶跃信号.各回路的输出响应曲线如图7所示.

观察分析图7的输出曲线，三种控制方案的输出都能够稳定在设定值，所以三种控制方案均具有良好的跟踪能力，但采用PID控制存在较大的超调量和调节时间，而LADRC控制和PI-LADRC控制没有超调量，调节时间较小.当分别向三条通道施加设定值时，PID控制的解耦能力差，难以取得令人满意的解耦效果.LADRC控制的解耦能力优于PID控制，但与PI-LADRC控制存在一定的差距.

为了使PI-LADRC控制的效果更有说服力，分别对三种控制策略下的超调量（σ%）和调节时间（ts）进行计算，计算结果如表2所示.

4.2 抗扰效果对比验证

在废液焚烧的过程中控制系统可能出现执行器误动作的现象，且废液燃烧时的热值实时变化，因而有必要衡量控制器的抗扰能力.

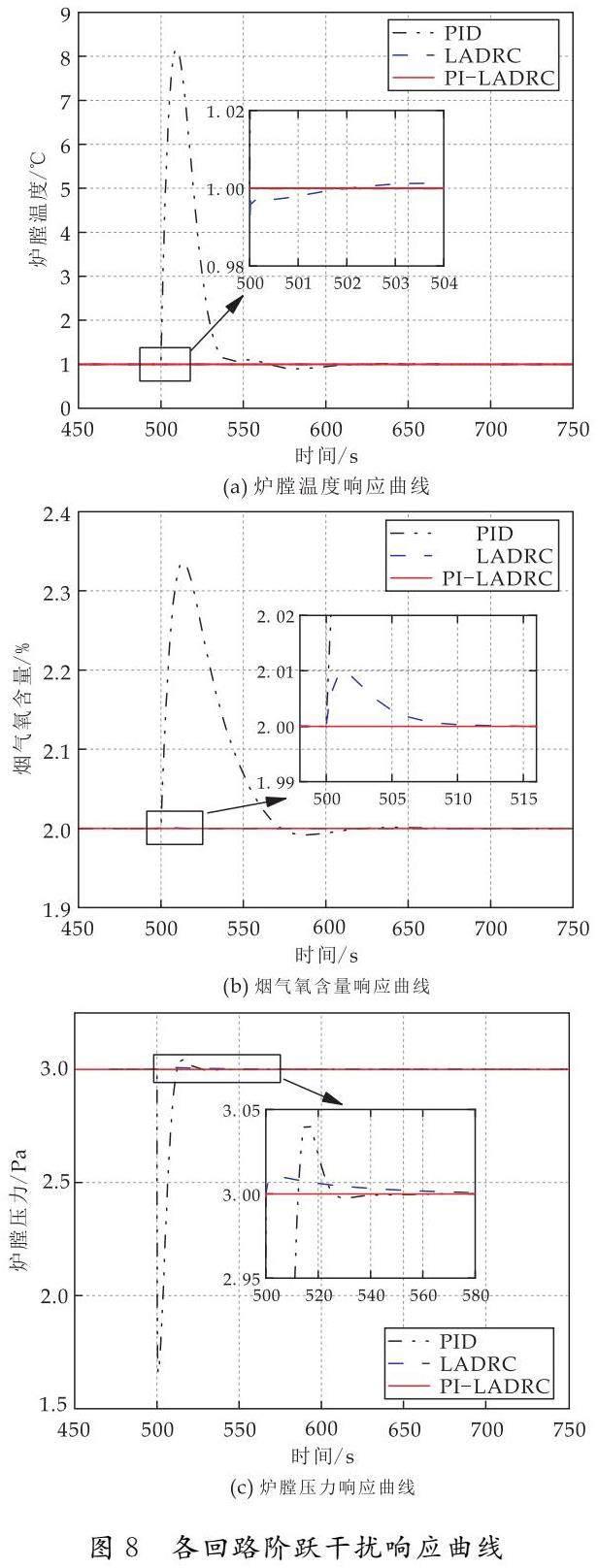
若执行器出现误动作的现象，可以将其等效为回路出现一个阶跃扰动信号，因此需要在上述实验的基础上研究控制器抗阶跃干扰的能力，当t=500 s时，分别向三条通道施加幅值为1的阶跃信号作为干扰，各回路的阶跃干扰响应曲线如图8所示.

由图8的响应曲线可知，以阶跃信号作为干扰，PID控制下各回路响应曲线均出现了大幅突变，LADRC控制下各回路响应曲线也出现了不同程度的变化，但比PID控制效果优秀，而采用PI-LADRC控制时各回路响应曲线未出现明显变化，这说明PI-LADRC控制对于阶跃信号干扰具有更好的抗扰能力.

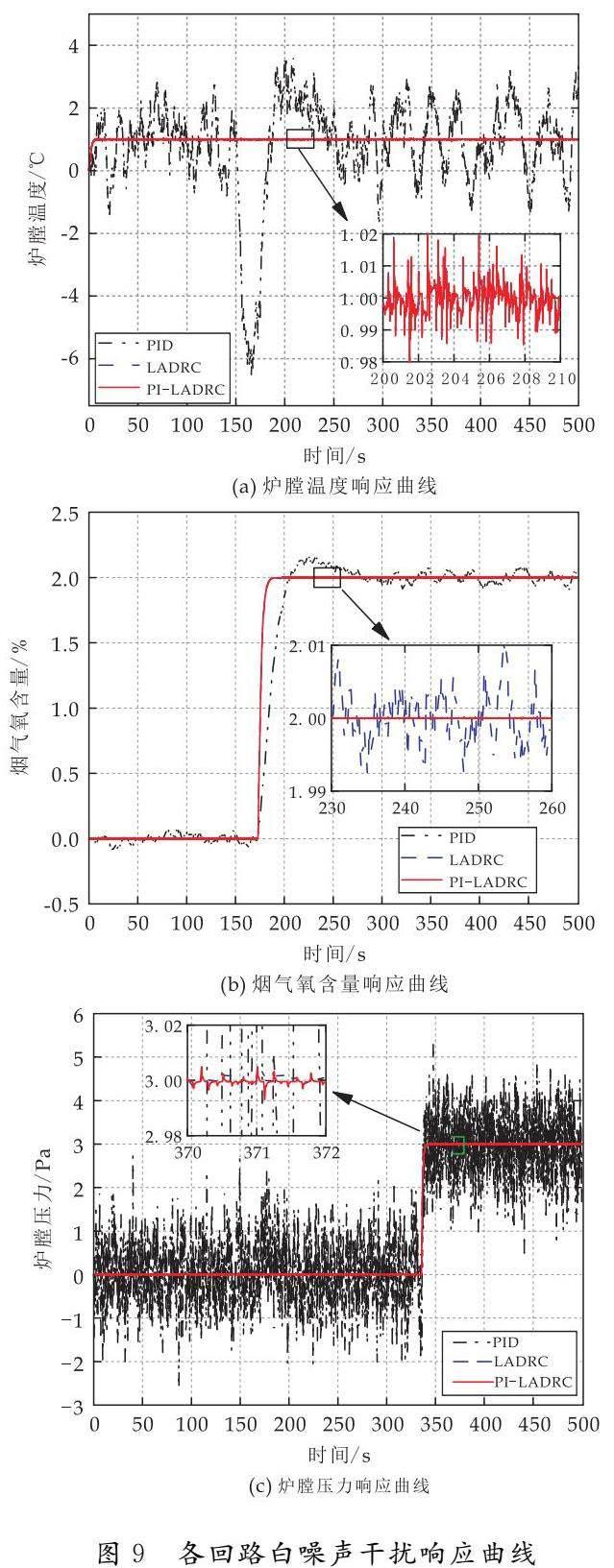
热值的变化会对系统的抗扰能力产生影响，而热值变化可以视为白噪声信号，因此在t=0时刻加入扰动信号.各回路加入白噪声干扰信号后的响应曲线如图9所示.

根据图9的响应曲线，加入白噪声干扰信号后，PID控制受到白噪声的干扰，导致控制回路的输出出现了不同程度的失真，LADRC控制受白噪声的影响较小，而PI-LADRC控制相较于LADRC控制所受的影响更小，并且能够更加快速的恢复稳定状态.

4.3 鲁棒性对比分析

本文采用蒙特卡洛实验验证控制器的鲁棒性，以4.1节的实验为基础，在保持仿真条件和控制参数不变的情况下，分别对主通道传递函数分母的最高次项增加或减少10%的参数摄动以及向主通道增加惯性环节（1/0.01s+1）来模拟模型失配情况.实验结果的参数摄动具体变化为：[SX（]-（46.484s+28.63）[]（6.3±0.63·i）s2+36.97s+5.72[SX）]，其中i=0，1，2，…，7，8.不同控制策略在模型失配情况下的控制曲线如图10～12所示.性能指标统计表3给出在蒙特卡洛实验下三种控制方案对于三条通道调节时间和超调量变化的范围.

根据图10～12和表3，采用三种控制方案对炉膛温度、烟气氧含量和炉膛压力进行控制，发生相同的参数摄动时，PID控制的超调量和调节时间远大于LADRC控制和PI-LADRC控制，LADRC控制的调节时间大于PI-LADRC控制.

PID控制的点集分布在整个区域内，LADRC控制和PI-LADRC控制的点集分布在较小的区域，且PI-LADRC控制分布的范围更小.这说明与 PID控制方案和LADRC控制方案相比，PI-LADRC控制在设定值跟踪方面的鲁棒性更强.

5 结论

针对LADRC控制带宽受限问题，本文通过理论推导和仿真分析验证了LESO的带宽和观测误差之间存在矛盾，提出了以低增益LESO為基础的PI-LADRC控制技术，通过仿真验证，PI-LADRC控制在观测器带宽取值较小的情况下能够解决焚烧过程存在的强耦合、时滞、强干扰等问题，相比于传统PID控制和LADRC控制具有更强的解耦能力、抗干扰能力和鲁棒性能.

参考文献

［1］ 钟 璟，韩光鲁，陈 群.高盐有机废水处理技术研究新进展［J］.化工进展，2012，31（4）：920-926.

［2］ 韩京清.从PID技术到“自抗扰控制”技术［J］.控制工程，2002，9（3）：13-18.

［3］ 韩京清.自抗扰控制技术［J］.前沿科学，2007（1）：24-31.

［4］ 李 杰，齐晓慧，夏元清.线性/非线性自抗扰切换控制方法研究［J］.自动化学报，2016，42（2）：202-212.

［5］ 高志强.自抗扰控制思想探究［J］.控制理论与应用，2013，30（12）：1 498-1 510.

［6］ Gao Zhiqiang.Scaling and bandwidth-parameterization based controller tuning［C］//Proceedings of the 2003 American Control Conference.Colorado，USA：IEEE，2003：4 989-4 996.

［7］ 顾 健，艾 勇，单 欣.线性扩张状态观测器的改进及在空间光通信粗跟踪的应用［J］.红外与激光工程，2016，45（3）：263-270.

［8］ 郭海宇，杨俊友，张晓光.永磁同步电梯门机改进型自抗扰控制策略［J］.哈尔滨工业大学学报，2018，50（9）：191-198.

［9］ 杜 鸣，牛玉广，潘翔峰，等.基于改进型模糊线性自抗扰控制器的SCR脱硝系统优化控制［J］.动力工程学报，2021，41（9）：743-748，757.

［10］ Jin H，Liu L，Lan W，et al.On stability and robustness of linear active disturbance rejection control：A small gain the orem approach［C］// Proceedings of the 36th Chinese Control Conference.Dalian，China：IEEE，2017：3 242-3 247.

［11］ 李 艳，胡 振，鱼 晨，等.面向控制的废液焚烧过程的建模与分析＼[J/OL＼].控制工程：1-9＼[2023-07-02＼].https：//doi.org/10.14107/j.cnki.kzgc.20200916.

［12］ 李鹏威，王 京.平整轧制多变量系统的线性自抗扰解耦控制［J］.武汉科技大学学报，2019，42（5）：339-342.

［13］ 吴 丹，赵 彤，陈 恳.快速刀具伺服系统自抗扰控制的研究与实践［J］.控制理论与应用，2013，30（12）：1 534-1 542.

［14］ 陈增强，郑月敏，孙明玮，等.含发电速率约束的三区域互联电力系统自抗扰控制［J］.哈尔滨工程大学学报，2020，41（9）：1 312-1 319.

［15］ 黄 宇，王佳荣.水轮机调速系统的线性自抗扰优化控制［J］.系统仿真学报，2016，28（12）：3 033-3 040.

［16］ 袁 东，马晓军，曾庆含，等.二阶系统线性自抗扰控制器频带特性与参数配置研究［J］.控制理论与应用，2013，30（12）：1 630-1 640.

［17］ 付 莹，李冰玉，郭继宁.基于线性自抗扰控制的高频真空感应炉温度控制［J］.中国铸造装备与技术，2020，55（3）：48-53.

［18］ 金辉宇，刘丽丽，兰维瑶.二阶系统线性自抗扰控制的稳定性条件［J］.自动化学报，2018，44（9）：1 725-1 728.

［19］ 黄 宇，张伟婷，金秀章.SCR脱硝系统的线性自抗扰串级控制研究［J］.中国电机工程学报，2018，38（18）：5 518-5 526.

【责任编辑：蒋亚儒】

基金项目：陕西省科技厅重点研发计划项目（2023-YBGY-277）; 陕西省咸阳市重点研发计划项目（L2022ZDYFSF047）

作者简介：李 艳（1972—），女，四川乐山人，副教授，研究方向：工业自动化、智能检测与智能控制