自激励广义二项门限自回归模型的统计推断

张洁 张玉 董小刚

摘要： 针对有上限且数据之间具有相依结构的非线性整数值时间序列数据的建模问题，提出一个自激励广义二项门限自回归模型. 首先，证明该模型的严平稳遍历性，并讨论模型的一些统计性质： 期望、 方差、 自协方差和转移概率; 其次，分别给出门限变量在已知和未知两种情形下模型参数的条件最大似然估计方法； 最后，将该模型应用到一组实际数据中进行拟合验证.

关键词： 整数值时间序列; 广义二项稀疏算子; 门限自回归过程; 条件最大似然估计

中图分类号： O212.1  文献标志码： A  文章编号： 1671-5489（2023）02-0275-10

Statistical Inference for Self-exciting GeneralizedBinomial Threshold Autoregressive Model

ZHANG Jie，ZHANG Yu，DONG Xiaogang

（School of Mathematics and Statistics，Changchun University of Technology，Changchun 130012，China）

Abstract： Aiming at the modeling problem of nonlinear integer-valued time series data with upper limit and dependent structure between

data，we proposed a self-exciting generalized binomial threshold autoregressive model. Firstly，we proved the strictly stationary and ergodicity of the model，

and discussed some statistical properties of the model，including the expectation，variance，aoto-covariance and the transition probability. Secondly，we gave the conditional maximum

likelihood estimation method of the model parameters in the case of known and unknown threshold variable. Finally，we applied the model to a set of real data for fitting verification.

Keywords： integer-valued time series; generalized binomial thinning operator; threshold autoregressive process; conditional maximum likelihood estimation

收稿日期： 2022-07-29.

第一作者简介： 张 洁（1992—），女，汉族，博士，讲师，从事整值时间序列分析、 假设检验和变量选择的研究，

E-mail： zhangjie@ccut.edu.cn. 通信作者简介： 董小刚（1961—），男，汉族，博士，教授，从事金融统计分析和生存分析的研究，E-mail： dongxiaogang@ccut.edu.cn.

基金項目： 国家自然科学基金（批准号： 11901053）、 吉林省自然科学基金（批准号： YDZJ202301ZYTS384）和吉林省教育厅科学技术研究项目（批准号： JJKH20220671KJ）.

1 引言与预备知识

整数值时间序列数据是一种较常见的计数数据. 由于传统的连续型时间序列数据不能有效地刻画整数值数据，Steutel等［1］提出了二项稀疏算子“”. 目前，关于整数值时间序列的研究已有很多结果. 在取值范围上，该类数据可分为无上限的整数值时间序列（{0，1，…}）和有上限的整数值时间序列（{0，1，…，n}）. 对取值范围没有上限的计数数据，Al-Osh等［2］提出了一阶整数值自回归（INAR（1））模型； Du等［3］将一阶整数值自回归模型推广到p阶，提出了INAR（p）模型； Neal等［4］和张哲等［5］研究了该类模型的估计问题； Fernndez-Fontelo等［6］提出了一个隐性INAR（1）模型，其中隐藏层是一个具有Poisson分布的随机过程，即Po-INAR（1）过程. 对有上限的计数数据，McKenzie［7］提出一个一阶整数值二项自回归（BAR（1））模型; Weiβ［8］研究了BAR（1）模型的性质并将其推广到高阶情形； Zhang等［9］将二项自回归过程推广到多项自回归过程； Davis等［10］给出了对整数值时间序列相关研究的综述.

上述模型均为线性模型，对具有非线性结构的整数值时间序列数据，Monterio等［11］基于二项稀疏算子，提出了一阶整数值门限自回归（SETINAR（2，1））模型，但该模型对有限计数范围内取值的数据无效； M?ller等［12］在文献［11］的基础上，提出了一个二项门限自回归（SETBAR（1））模型； Yang等［13］研究了SETBAR（1）模型的性质并将该模型应用于麻疹数据的研究中; 李晗［14］在文献［13］的基础上研究了该模型的经验似然推断问题.

由于二项稀疏算子存在Bernoulli计数序列独立同分布假设的局限，因此不能很好地解释具有相依性的数据. 为解决该问题，Ristic＇等［15］提出了一类新的广义二项稀疏算子“θ”，该算子能有效考虑个体之间具有相依结构的情形； 进一步，为刻画具有相依结构的有上限整数值时间序列数据，Kang等［16］将广义二项稀疏算子与BAR（1）模型相结合，提出了广义二项自回归（GBAR（1））模型，但该模型无法刻画非线性整数值时间序列. 因此，本文在文献［16］的基础上，提出一个一阶自激励广义二项门限自回归（TGBAR（1））模型，进行相应的统计推断，并讨论该模型的统计性质和参数的条件极大似然估计问题. 最后给出该模型的数值模拟以及在实际数据中的应用.

结果为2.264 9，其中μ和σ2分别为样本均值和样本方差. BID的结果表明，数据自身具有过度分散的性质. 为说明模型的拟合效果，将TGBAR（1）模型应用于该数据集，并与BAR（1）模型、 GBAR（1）模型和SETBAR（1）模型进行对比，结果列于表3. 由表3可见，相比于其他3种模型，本文模型能更有效地拟合所生成的随机数，同时更准确地估计出数据自身的统计性质，进一步说明通过TGBAR（1）模型生成的随机数对模型的识别效果更好.

5 实例分析

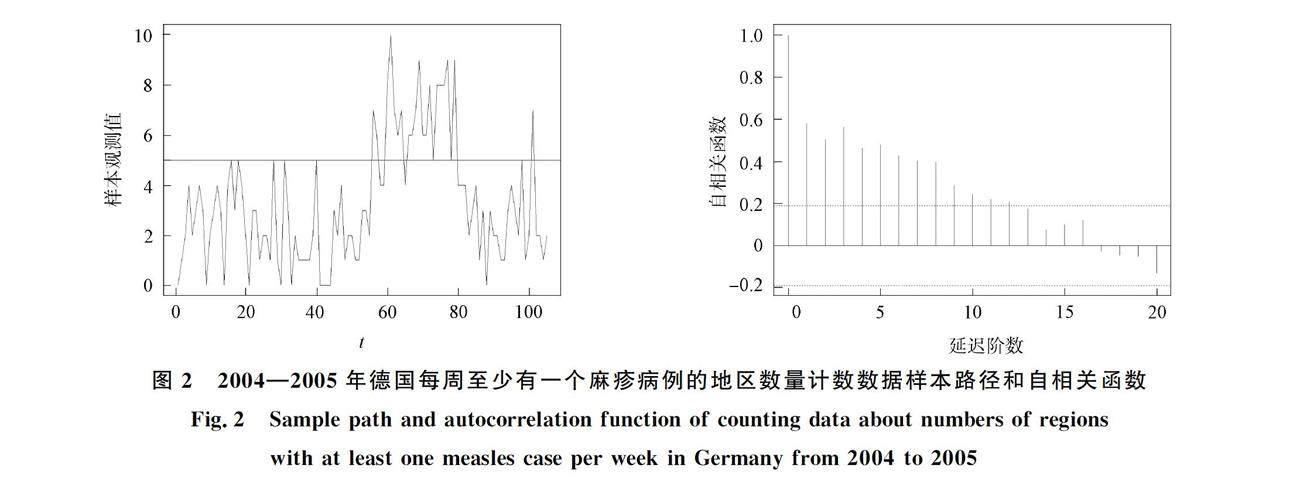
实例分析数据采用2004—2005年德国的38个地区，每周至少有一个新的麻疹病例的地区数量计数数据，数据集来自于SurvStat（Robert-Koch-Institut; https：//www.rki.de/EN/Home/homepage_node.html）. 该组数据共105个数据点，每个点的取值范围为{0，1，…，n}，n=38由德国给定的地区数量确定. 图2为该组数据的样本路径和自相关函数.

由图2可见，数据是平稳的，并表现出一定的门限特征，因此可考虑用本文提出的TGBAR（1）模型对数据进行拟合. 图2中横线为通过TGBAR（1）模型预测出的门限值，该门限值有效地将数据划分成两部分，表明了本文模型对门限值预测的有效性. 同时，选用 BAR（1）模型、 GBAR（1）模型和SETBAR（1）模型进行对比实验.

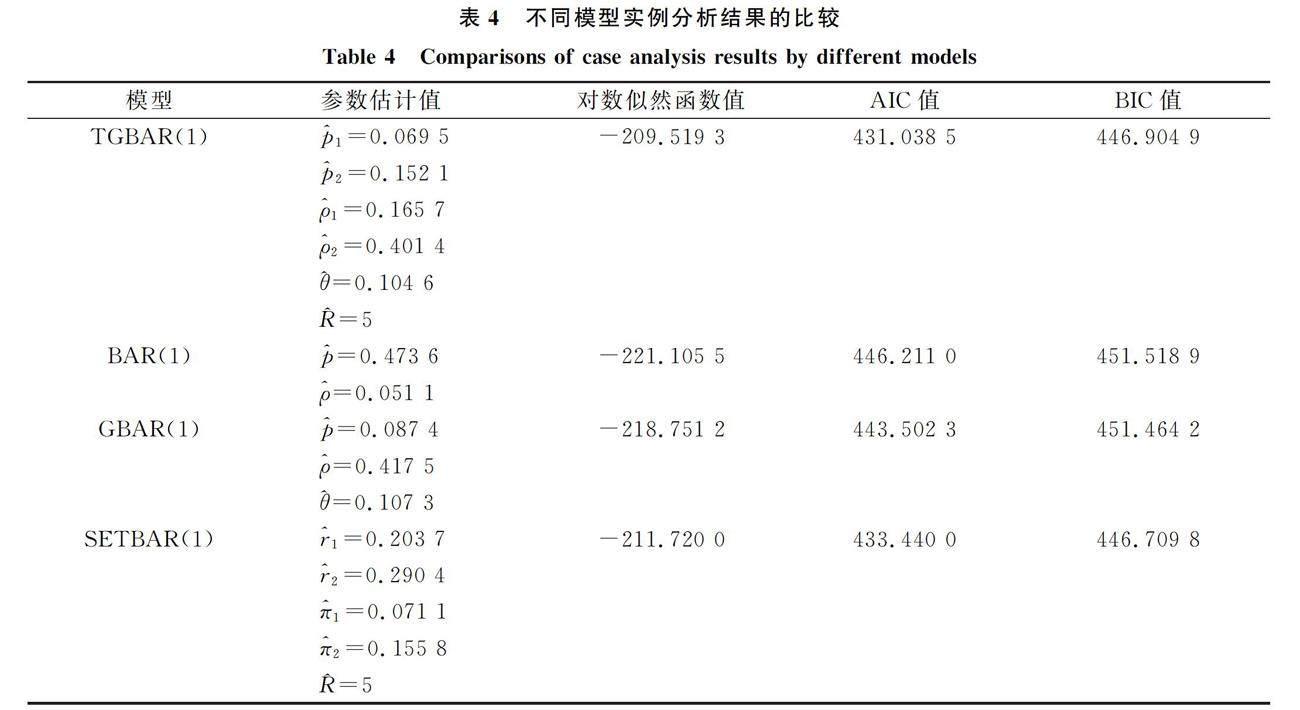
对上述模型分别给出参数的条件极大似然估计值、 对数似然函数值、 AIC值和BIC值，结果列于表4. 由表4可见，由于TGBAR（1）模型的参数个数较多，导致BIC的结果比SETBAR（1）模型略差，但TGBAR（1）模型的对数似然函数值最大，AIC值最小，仍能说明该模型拟合的优势. 因此，表明TGBAR

（1）模型可以对有上限且个体之间具有相依结构的非线性整数值时间序列数据进行有效的刻画和分析.

综上所述，本文基于一阶广义二项自回归模型，提出了一阶自激励广义二项门限自回归模型. 首先，得到其均值、 方差、 自协方差和转移概率，并证明了模型的严平稳遍历性. 其次，分别在门限已知和未知的情形下，给出了参数的条件极大似然估计方法. 模拟结果表明，有效的门限参数估计能保证其他参数的估计效果. 最后，将该模型应用于德国新感染麻疹的区域数目病例研究中，模拟结果表明，TGBAR（1）模型能较好地拟合有上限且数据之间具有相依结构的非线性整数值时间序列数据.

参考文献

［1］ STEUTEL F W，VAN HARN K. Discrete Analogues of Se

lf-decomposability and Stability ［J］. The Annals of Probability，1979，7（5）： 893-899.

［2］ AL-OSH M A，ALZAID A A. First-Order Integer-Valued Autoregressive （INAR

（1）） Process ［J］. Journal of Time Series Analysis，1987，8（3）： 261-275.

［3］ DU J G，LI Y. The Integer-Valued Autoregressive （IN

AR（p）） Model ［J］. Journal of Time Series Analysis，1991，12（2）： 129-142.

［4］ NEAL P，SUBBA RAO T. MCMC for Integer-Valued ARMA P

rocesses ［J］. Journal of Time Series Analysis，2010，28（1）： 92-110.

［5］ 張哲，张海祥，张卓飞，等. INAR（1）模型参数的Bayes 估计 ［J］. 吉林大学学报（理学版），2010，48（6）： 931-935. （ZHANG Z，ZHANG H X，Z

HANG Z F，et al. Bayesian Estimation of Parameters in the INAR（1） Model ［J］. Journal of Jilin University （Science Edition），2010，48（6）： 931-935.）

［6］ FERNNDEZ-FONTELO A，MORIA D，CABAA A，et al. Estimating the Real

Burden of Disease under a Pandemic Situation： The SARS-CoV2 Case ［J］. PLOS One，2020，15（13）： e0242956-1-e0242956-20.

［7］ McKENZIE E. Some Simple Models for Discrete Variate Ti

me Series ［J］. Journal of the American Water Resources Association，1985，21（4）： 645-650.

［8］ WEIβ C H. A New Class of Autoregressive Models for

Time Series of Binomial Counts ［J］. Communications in Statistics： Theory and Methods，2009，38（4）： 447-460.

［9］ ZHANG J，WANG D H，YANG K，et al. A Multinomial Autoregressive

Model for Finite-Range Time Series of Counts ［J］. Journal of Statistical Planning and Inference，2020，207： 320-343.

［10］ DAVIS R A，FOKIANOS K，HOLAN S H，et al. Count Time

Series： A Methodological Review ［J］. Journal of the American Statistical Association，2021，116： 1533-1547.

［11］ MONTERIO M，SCOTTO M G，PEREIRA I. Integer-Valued

Self-exciting Threshold Autoregressive Processes ［J］. Communications in Statistics： Theory and Methods，2012，41（15）： 2717-2737.

［12］ MLLER T A，SILVA M E，WEIβ C H，et al. Se

lf-exciting Threshold Binomial Autoregressive Processes ［J］. AStA Advances in Statistical Analysis，2016，100（4）： 369-400.

［13］ YANG K，WANG D H，LI H. Threshold Autoregression Analysis for Finite-Range Time Series of Counts with an Application on Measles Data

［J］. Journal of Statistical Computation and Simulation，2018，88（3）： 597-614.

［14］ 李晗. 几类整数值门限时间序列模型的统计推断 ［D］. 长春： 吉林大学，2018. （LI H. Statistical Inference for Several Classes of Integer

-Valued Threshold Time Series Models ［D］. Changchun： Jilin University，2018.）

［15］ RISTIC＇ M M，NASTIC＇ A S，MILETI

C＇ ILIC＇ A V. A Geomet

ric Time Series Model with Dependent Bernoulli Counting Series ［J］. Journal of Time Series Analysis，2013，34（4）： 466-476.

［16］ KANG Y，WANG D H，YANG K. Extended Binomial AR（1） Proces

ses with Generalized Binomial Thinning Operator ［J］. Communications in Statistics： Theory and Methods，2020，49（14）： 3498-3520.

［17］ ROSS S M. Stochastic Processes ［M］. New York： John Wiley & Sons，1996： 175.

［18］ BILLINGSLEY P. Statistical Inference for Markov Processes ［M］. Chicago，IL： University of Chicago Press，1961： 10-23.

［19］ WANG C，LIU H，YAO J F，et al. Self-excited Threshold Poiss

on Autoregression ［J］. Journal of the American Statistical Association，2014，109： 777-787.

［20］ CHENG X X，LI W K，YU P L H，et al. Modeling Threshold Conditional Heteroscedasticity

with Regime-Dependent Skewness and Kurtosis ［J］. Computational Statistics & Data Analysis，2011，55（9）： 2590-2604.

（責任编辑： 李 琦）