考虑多方利益的大规模共享停车匹配优化策略
2023-04-29王震邦宋运忠
王震邦 宋运忠
摘要: 为有效缓解大规模停车时的停车乱、停车难问题,围绕停车费用、排队时间以及均衡多个停车场之间的停车需求,构建兼顾多方利益凸优化模型。首先,利用匹配博弈推导出最小化停车费用的稳定双边匹配;然后,同时考虑多方利益来扩展研究,构建的数学模型为凸优化问题,使用交替方向乘子法(ADMM)分布式求解;最后,仿真结果表明基于ADMM分布式优化模型与匹配博弈算法和贪心算法相比,可以满足多方利益,从隐私保护、计算时间与数据传递量等方面分析验证了ADMM分布式优化模型比集中式优化模型更适用于大规模共享停车匹配,并分析验证了考虑多方利益的必要性与权重系数对计算结果的影响。
关键词: 大规模停车匹配;多方利益;匹配博弈;交替方向乘子法
中图分类号: TP273.1;U491.7文献标识码: A
收稿日期: 2021-09-27;修回日期:2022-02-28
基金项目: 国家自然科学基金(61340041,61374079);河南省自然科学基金(182300410112)
第一作者: 王震邦(1997-),男,河南郑州人,硕士研究生,主要研究方向为复杂系统建模与控制。
通信作者: 宋运忠(1968-),男,河南民权人,博士,教授,主要研究方向为复杂系统的分析与控制。
A Massive Shared Parking Matching Optimization Strategy Considering the Interests of Multiple Parties
WANG Zhenbang, SONG Yunzhong
(School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, China)
Abstract:In order to effectively alleviate the problem of parking chaos and difficult parking during massive parking, this paper builds a convex optimization model that takes into account the interests of multiple parties, focusing on parking costs, queuing time and balancing the parking demand among multiple parking lots. First, a stable bilateral matching that minimizes parking fees is derived by using a matching game; then, the research is extended considering the interests of multiple parties at the same time, and the mathematical model constructed is a convex optimization problem, which is solved by the alternating direction multiplier method (ADMM) distributed solution. Finally, the simulation results show that the distributed optimization model based on ADMM can meet the interests of multiple parties compared with the matching game algorithm and the greedy algorithm. It is verified that the ADMM distributed optimization model is more efficient than the centralized optimization model from the aspects of privacy protection, computing time and data transfer volume. It is suitable for massive shared parking matching, and the necessity of considering the interests of multiple parties and the influence of weight coefficients on the calculation results are analyzed and verified.
Key words: massive parking matching; multi-party interests; matching game; alternating direction multiplier method
0 引言
據公安部统计,截止到2021年3月,中国机动车保有量达3.7亿辆。在人口密集的城市里找到停车位是个不小的挑战。此外,30%的交通拥堵是由于停车巡游引起的,不仅会造成交通拥堵,而且会产生额外的燃油消耗与空气污染[13]。
因此,学术界和工业界关于停车匹配问题的研究主要集中在如何将车辆匹配给最接近目的地的可用停车场,从而最大限度减少停车匹配的成本。譬如:Wu等[4]为自动驾驶车辆寻找最短路径,最小化停车成本;Kotb等[5]的目标是同时提高停车资源利用率、增加停车场收入与减少停车成本。Xu等[6]利用最小化停车场到车辆目的地的最大距离,实现公平停车分配。以上的文献都只解决了单个停车场的分配问题,忽视了多个停车场之间的潜在合作。卢凯等[7]在考虑司机个体对于步行距离与停车场收费的心理意愿的前提下,实现了停车诱导系统虚拟总成本最小化;Lin等[8]旨在保证停车服务质量的同时,最大化停车场的效益;Schlote等[9]提出了一种负载平衡算法来平衡多个停车场的需求;Kim等[10]利用分布式算法在均衡多个停车场之间停车需求的前提下,降低停车费用。当前工作暂无同时考虑多方停车利益的研究,本文将考虑多方利益以使系统更高效。
目前,关于停车诱导系统的研究主要分为两类:基于传感器的方法和基于路边单元(Road Side Units, RSUs)的方法。在基于传感器的方法中[1112],用户必须把注意力分散给移动设备,具有严重的交通隐患。基于RSUs的车载自组织网络可以提高道路安全,并带来更好的驾驶体验[1314],但不同停车场之间的交流是由多个RSUs来共同完成的,则多个RSUs必须使用同步机制[15],此机制成本较为昂贵。关于共享停车场的匹配策略,必须考虑所有可用资源。当许多地区具有大规模的空闲车位时,以上方法就暴露了缺点。因此,本文提出了一种基于雾服务器和路边云的停车诱导系统,低成本地、高效地进行停车匹配。
本文针对大规模共享停车匹配问题,采用匹配博弈算法实现最小化停车费用的稳定双边匹配,采用交替方向乘子法(Alternating direction method of multipliers, ADMM)来实现多方利益。最后利用Matlab进行仿真与分析,证明了所提方案的有效性与可行性,同时对比分析了集中式优化算法、匹配博弈算法与贪心算法,证明了基于ADMM的算法的优势。
1 系统模型与模型构建
1.1 系统组件及其原理
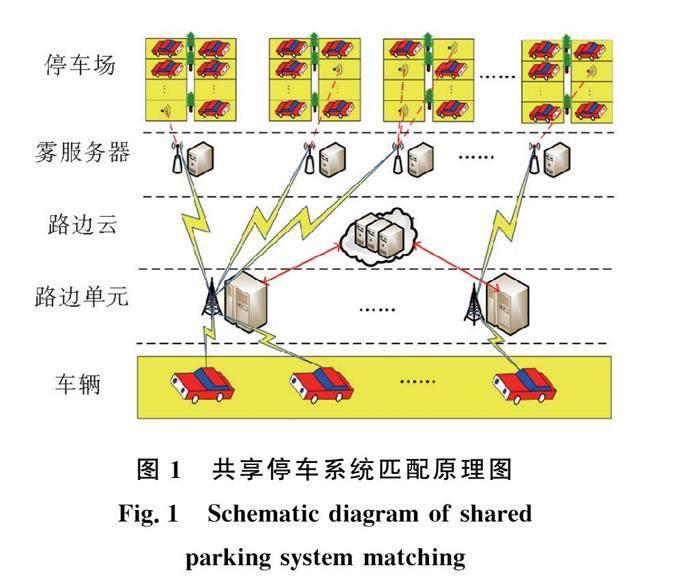
如图1所示,在智能城市中,一个停车诱导系统可以控制多个共享停车场系统。
1)停车场与车辆:系统考虑大规模车辆与多个停车场的停车资源共享。停车场向雾服务器提供每个停车位的状态(占用或空闲)。车辆包括共享汽车与私人车主。私人停车场与私人车主将被激励参与有序停车,停车场与车主都将获得经济利益。
2)雾服务器:扮演着停车场与RSUs之间信息交换的角色。通过WIFI和Zigbee等无线网络收集全部停车位的状态,将信息传输至RSUs。
3)RSUs:主要负责与车辆进行交互,连接其通讯范围内车辆,向司机广播停车位数据,为它们找到最佳停车位置。一方面,RSUs需要跟踪有限的空闲车位,另一方面还需要优化控制。因此,这部分可以充当模型的控制中心。
4)路边云:路边云在RSUs之间起到中间层的作用,交换不同停车位的信息。由于RSUs的通信范围有限,路边云帮助两个RSUs进行信息交换。路边云的存在,使司机可以随时随地向RSUs发送自己的停车需求。
1.2 构建数学模型
1.2.1 模型假设
在模型构建中,对停车匹配问题进行适当的简化,作以下假设:
1)假设有停车需求的车主对所有停车场与停车位都没有特殊的偏好;
2)假设单个停车场的所有车位属性与费用相同,且仅考虑按照时长收费;
3)假设停车场供应商与车主都严格遵守系统规则与停车时间;
4)假设车辆的当前位置、目的地位置以及停车场的位置都是二维欧几里得空间,R2;
5)假设车主会根据实际需求提交相关属性信息,且一定会接受匹配结果。
4 算例分析
本文在2 000 m×2 000 m的毗邻区域,设计了一种网格式路网[9]。路网中随机生成1 000辆平均行驶速度为40 km/h、停放时间服从平均值为2 h的指数分布的待匹配车辆,为保证实验结果具有代表性,将待匹配车辆的起点与目的地位置都随机设置在区域中,停车场的位置也均匀分布在区域中,且数据均不同,如表3所示。为兼顾多方主体的目标,权重系数δ1,δ2与δ3分别为5×10-4,1×10-4与1×10-4。
本文涉及的算法主要有:1)集中式优化:本文调用GUROBI来获得最优解,考虑了系统的整体效率;2)ADMM分布式优化:对式(18)进行分布式求解,各子问题通过调用GUROBI求解器进行求解,收敛精度为10-4;3)匹配博弈算法:考虑车主与停车场供应商的偏好,得到一个稳定双边匹配;4)贪心算法:为停车场就近匹配车辆,直到满足其可服务车辆上限。本文的算例均在CPU为AMD Ryzen7 4 800H、主频2.9 GHz、内存为16G的计算机上采用MATLAB R2019a实现建模。
4.1 各算法的优化结果性能对比
各算法的加权平均总成本比较如图4所示,优化结果对比数据如表4所示。
可以观察到,由于集中式优化是最优结果,因此得到的总成本最低。ADMM分布式优化的初始状态与最优结果的差距较大,然而,当算法满足收敛,ADMM分布式优化得到了近似最优解,计算结果基本吻合,说明在误差允许的范围内,二者模型可以看作等价。间隙是由于松弛投影二进制变量x产生的误差,可忽略不计。因此ADMM分布式优化优于匹配博弈算法与贪心算法。匹配博弈算法降低车主停车费用方面的性能较强,由于贪心算法为车辆匹配较近的停车场,最小化停车场排队时间的性能较强。
4.2 模型可行性分析
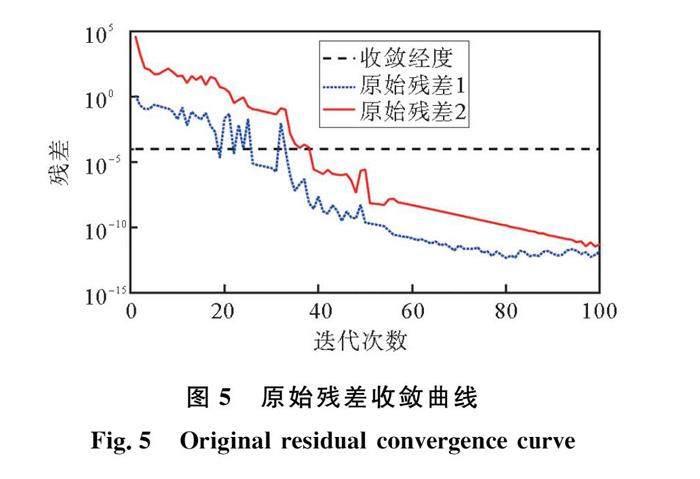
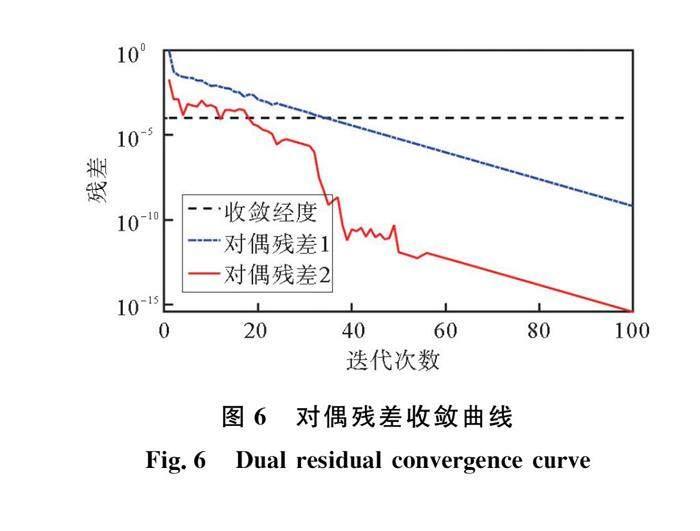
分布式模型是否能够应用于工程实际应用,取决于算法的收敛性能。图5、图6給出了分布式优化下的残差变化曲线,由于本文模型考虑两个线性等式耦合,故存在两组对偶更新。所有残差均可以在迭代40次收敛,根据测试分析,每次子问题的迭代时间不超过0.5 s。在实际应用中,通讯时延0.1 s后,可在30 s内达到收敛。与此同时,与集中式优化相比,ADMM分布式优化对子问题的计算量和内存占用量大大减小。通信数据仅包括分配策略、拉格朗日乘子等信息,通信负载很小,且不含任何私密信息,有利于保护用户的隐私[20]。因此,本文的模型适合于未来大规模共享停车匹配。
4.3 单目标与权重系数对计算结果的影响
为验证考虑多方利益的必要性,利用ADMM分布式优化将本文模型与3种单目标模型进行对比。目标1:本文模型;目标2:仅考虑最小化车主的停车费用;目标3:仅考虑最小化停车场的排队时间;目标4:仅考虑均衡多个停车场的停车需求。表5列出了3种不同匹配目标下的计算结果,考虑多方利益匹配方案的加权平均总成本最低。目标2~4没有兼顾到全局的利益,无法实现长久互利共赢。因此,考虑综合效益的模型十分必要。
為分析权重系数对计算结果的影响,表6对比了7组不同权重系数的计算结果。各组中δ1的取值分别为5×10-3,5×10-4,5×10-4,0,5×10-4与5×10-4,δ2的取值分别为1×10-4,1×10-3,1×10-4,1×10-4,0与1×10-4,δ3的取值分别为1×10-4,1×10-4,1×10-3,1×10-4,1×10-4与0。观察权重系数组1~3可知,过于偏重某一目标对计算结果会造成一定的影响,不可避免地损害了其他目标的利益;观察权重系数组5~7可知,如若少考虑一方利益,将严重损害被忽略方的利益。因此,在实际应用中,需合理地选择权重系数,使得各目标均衡。
5 结论
针对大规模共享停车匹配问题,为了有效利用资源,整合公共和私人停车场,目标是在均衡多个停车场之间的停车需求的条件下,降低停车费用与停车排队时间。首先,基于匹配博弈得到最小化停车费用稳定双边匹配。然后,考虑多方利益构造了一个凸优化问题,利用ADMM算法进行分布式优化。仿真算例表明:匹配博弈算法可以更有效地降低停车费用,满足停车场与车辆的偏好的同时,得到稳定双边匹配;ADMM分布式优化同时均衡多个停车场之间的停车需求、降低停车费用与排队时间,且分布式优化注重个体独立性与隐私保护,更适合于大规模共享停车匹配问题的工程实际应用。随着道路上电动汽车的剧增,车主、充电站和电网三方利益的充电问题将是未来研究的重点。
参考文献:
[1]SHOUP D C. Cruising for parking[J]. Transport Policy, 2006, 13(6): 479-486.
[2]KONG T R, XU S, CHENG M, et al. Iot-enabled parking space sharing and allocation mechanisms[J]. IEEE Transactions on Automation Science and Engineering, 2018, 15(4): 1654-1664.
[3]BOCK F, MARTINO S D, ORIGLIA A. Smart parking: using a crowd of taxis to sense on-street parking space availability[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(2): 496-508.
[4]WU M, JIANG H, TAN C A. Automated parking space allocation during transition with both human-operated and autonomous vehicles[J]. Applied Sciences, 2021, 11(2): 855.
[5]KOTB A, SHEN Y, ZHU X, et al.IParker—a new smart car-parking system based on dynamic resource allocation and pricing[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(9): 2637-2647.
[6]XU Y, ALFONSETTI E, Weeraddana P C, et al. A semidistributed approach for the feasible min-max fair agent-assignment problem with privacy guarantees[J]. IEEE Transactions on Control of Network Systems, 2016, 5(1): 333-344.
[7]卢凯, 林茂伟, 邓兴栋, 等. 停车总成本最小的停车位动态匹配与诱导模型[J]. 华南理工大学学报(自然科学版), 2018, 46(9): 82-91,98.
LU K, LIN M W, DENG X D, et al. A dynamic allocation and guidance model for parking spaces with minimum total parking costs[J]. Journal of South China University of Technology(Natural Science Edition) , 2018, 46(9): 82-91,98.
[8]LIN J, CHEN S Y, CHANG C Y, et al. SPA: smart parking algorithm based on driver behavior and parking traffic predictions[J]. IEEE Access, 2019, 7, 34275-34288.
[9]SCHLOTE A, KING C, CRISOSTOMI E, et al. Delay-tolerant stochastic algorithms for parking space assignment[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 1922-1935.
[10] KIM O T T, TRAN N H,PHAM C, et al. Parking assignment: minimizing parking expenses and balancing parking demand among multiple parking lots[J]. IEEE Transactions on Automation Science and Engineering, 2020, 17(3): 1320-1331.
[11] 林小围, 周晶, 卢珂. 私家车位共享系统的车位动态预约与分配[J]. 系统工程理论与实践, 2018, 38(11): 189-199.
LIN X W, ZHOU J, LU K. Dynamic reservation and allocation in private parking slot sharing system[J]. Systems Engineering-Theory & Practice, 2018, 38(11): 189-199.
[12] GARRA R, MARTNEZ S, SEB F. A privacy-preserving pay-by-phone parking system[J]. IEEE Transactions on Vehicular Technology, 2017, 66(7): 5697-5706.
[13] LIU P, XU B, DAI G, et al. MDP: minimum delay hot-spot parking[J]. Journal of Network and Computer Applications, 2017, 87: 210-222.
[14] LIU H, QIU T, ZHOU X, et al. Parking-area-assisted spider-web routing protocol for emergency data in urbanVANET[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 971-982.
[15] LU R, LIN X, ZHU H, et al. Spark: a new VANET-based smart parking scheme for large parking lots[C]// Rio de Janeiro, Brazil: IEEE Infocom, 2009,2009.
[16] GALED, SHAPLEY L S. College admissions and the stability of marriage[J]. American Mathematical Monthly, 1962, 69(1): 9-15.
[17] ROTH A E. Deferred acceptance algorithms: history, theory, practice, and openquestions[J]. International Journal of Game Theory, 2008, 36(3): 537-569.
[18] 李伟钢, 唐朝生, Antonio C de A Junior, 等. 航空交通协同决策方法研究[J]. 复杂系统与复杂性科学, 2015, 12(2): 46-52.
LI W G, TANG C S, ANTONIO C DE A J, et al. A study on collaborative decision making in air transportation[J]. Complex Systems and Complexity Science, 2015, 12(2): 46-52.
[19] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations & Trends in Machine Learning, 2010, 3(1): 1-122.
[20] 潘振寧, 余涛, 王克英. 考虑多方主体利益的大规模电动汽车分布式实时协同优化[J]. 中国电机工程学报, 2019, 39(12): 3528-3541.
PAN Z N,YU T,WANG K Y. Decentralized coordinated dispatch for real-time optimization of massive electric vehicles considering various interests[J]. Proceedings of the CSEE, 2019, 39(12): 3528-3541.
(责任编辑 李 进)
