考虑氮素流通效率的生态补偿策略演化博弈分析
2023-04-29张骥骧陈晓竹
张骥骧 陈晓竹


摘要:
基于流域氮素流通效率提升,探讨地方政府与农户的生态补偿策略选择,构建有限理性地方政府与农户的演化博弈模型,仿真分析演化均衡策略,提出补偿力度随农户行为变化的动态生态补偿政策,有利于政府长期优化政策和响应需求。研究表明:静态生态补偿政策下系统存在均衡稳定策略,且双方的初始合作比例直接影响系统演化速率;动态政策下演化轨迹螺旋式趋近混合策略焦点,可通过控制生态补偿上限等因素提升合作概率。
关键词:
氮素流通效率;演化博弈;生态补偿;演化稳定策略
中图分类号: F205;F224.32 文献标识码:A
收稿日期:2022-01-16;修回日期:2022-03-21
基金项目:
国家自然科学基金(71101071);中央高校基本科研业务费专项资金(NS2019045)
第一作者:
张骥骧(1978-),男,安徽淮南人,博士,副教授,主要研究方向为有限理性博弈与企业经营过程分析与决策。
通信作者:
陈晓竹(1998-),女,江苏无锡人,硕士研究生,主要研究方向为管理科学及决策理论与方法。
Evolutionary Game Analysis of Ecological Compensation Strategies
Considering Nitrogen Circulation Efficiency
ZHANG Jixiang, CHEN Xiaozhu
(College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)
Abstract:
Based on the enhancement of nitrogen circulation efficiency in the watersheds, this paper explores ecological compensation strategy choices of decision-makers, constructs an evolutionary game model of boundedly rational local governments and farmers, and simulates the evolutionary equilibrium strategies. A dynamic ecological compensation policy is proposed, where compensation intensity changes with farmers' behavior, which is conducive to the government's long-term optimization of its policies. The study shows that there exists an equilibrium stability strategy for the system under static ecological compensation policy, meanwhile, the initial cooperation ratio of both parties directly affects the evolutionary rate of the system; the evolutionary trajectory under dynamic policy spirals towards a mixed strategy focus, and the cooperation ratio can be elevated by controlling the ecological compensation ceiling and other crucial factors.
Key words:
nitrogen cascade efficiency; evolutionary game; ecological compensation; evolutionary stabilization strategy
0 引言
在自然演化和人類社会活动中,氮素的有效利用和排放总量控制是一个热点问题。随着各级政府相关政策的出台,目前水体富营养化的根源已由工业废水等形成的点源污染逐渐转变为农业生产中农药化肥进入水体形成的面源污染[1]。针对目前中国各水系流域氮素输入的特点,本文从农业氮素流通效率角度出发,探讨流域内氮素利用效率及总量控制的生态补偿政策问题。
近年来针对流域氮素流通效率的研究,主要是基于N-Calculator等模型进行区域氮足迹分析,如徐昌城等[2]对闽江流域氮足迹的动态变化进行了估算,分析了水质响应与氮素利用效率的关系;李春喜等[3]分析了不同施氮水平对农田的生产氮足迹的影响。对于农业氮循环的研究大多是基于实验位点和区域尺度的技术性分析,缺少基于区域经管角度利益相关者的决策行为的研究。
多名国内外学者强调,如果政府希望农户采取环保的耕作措施,采用刺激性经济手段进行合理补偿是最佳选择[4]。实验表明,相比传统的“强制性”政策,“激励型”生态补偿政策效果更好[5]。Kelley[6]的研究显示,适当的经济补助对农户参与环境政策的激励效应十分明显。目前政府补贴农户的主要方式中,资金补偿是最常见和最迫切需要的补偿方式[7]。吕悦风[8]的研究表明补偿标准是影响农户参与意愿的决定性因素。焦建玲等[9]进一步提出政府的补偿强度应根据补偿对象的行为而变化。
演化博弈在相关研究中得到了广泛的运用:1)分析流域上下游政府共同实施生态补偿的跨界合作问题,如徐大伟等[10]分析了上下游政府在流域生态补贴下演化博弈的特点和结果,证明了流域的生态补偿需要中央政府的适度干预;李昌峰等[11]构建非参数回归计量模型验证了上级监督部门约束的必要性。2)探讨辖区内补偿对象之间的博弈关系,如付秋芳等[12]研究了惩罚机制下供应链企业碳减排的演化博弈策略;崔浩等[13]研究了有限理性条件下拥有所有制配置权的企业共同参与生态治理并达到 Nash 均衡的过程。
本文假设流域范围内农业生产氮循环过程中的利益相关主体为当地政府和农户两个群体,采用演化博弈分析方法探讨双方的博弈均衡策略,模拟系统均衡点与演化轨迹,为各级管理机构的政策制定提供理论支撑。本文主要创新点有:基于流域氮素流通效率提升,从区域经济和管理角度出发,通过有限理性演化博弈研究了政府与农户生态补偿策略选择的动态演化规律与均衡策略;提出补偿力度随农户行为变化的动态生态补偿政策,有利于政府长期优化政策和响应农户需求;重点分析了动态补偿政策下政府与农户决策的关键影响因素,提出了增大农户合作比例的对策建议。
1 静态生态补偿政策下的演化博弈模型
1.1 模型的构建
假设流域氮素流通效率提升的博弈中仅存在地方政府与农户两个有限理性的博弈主体,政府为实现综合利益最大化不断调整生态政策,农户为实现自身利润最大化选择是否改进耕作措施。
政府作为生态保护主导者为农户提供不同激励措施:1)通过技术推广进行内源激励,从根本上提升农户对生态政策的认知,然而农户习惯性的生产行为将产生一定阻力。2)应用经济手段进行外源激励,通过各种指标监管农户的生产行为。因此,地方政府博弈行为策略空间为(补偿A,不补偿B)。在内源与外源激励的驱动下,农户可能积极合作,也可能为保证农产品产量降低资金投入,不积极参与氨氮污染治理行动。因此,农户博弈行为策略空间为(合作C,不合作D)。构建演化博弈系统(I),对有限理性地方政府与农户做出假设:
1)当农户选择合作策略,获得固定的生态补偿S;氮肥滥用造成的面源污染得到治理,产生的额外收益记为B1;同时,为避免降低农产品产量,在农产品价格与消费者偏好等条件不变的情况下,同等产量水平下农户需要额外支付提升氮肥利用率带来的技术成本C。
2)当农户选择不合作策略,基本生产收益为B0,氮素在农业生产环节大量流失并进入到生态循环中,对农村水环境带来潜在破坏,对未来农业生产存在负面影响,将生态环境损害对农户造成的损失记为D。
3)当地方政府选择补偿策略,记地方政府对中央环保政策的执行强度为θ,受政策执行过程中多种因素的综合影响,记0<θ<1;假设政策执行强度达到理想的完美条件时地方政府监管部门投入费用为σ,实际投入费用为θσ;若农户选择合作后流域水环境有所改善,地方政府将得到上级政府的横向奖励μ。
4)当地方政府选择不补偿策略,包含税收等的基本收益为w;若农户拒绝改变耕作措施,对生态环境产生负面影响,政府需承担社会舆论成本为ρ。
根据以上假设,得出流域氮素流通效率提升的演化博弈收益矩阵,如表1所示。
1.2 演化均衡点分析
假设地方政府采取补偿政策的概率为x(x∈0,1),采取不补偿政策的比例为1-x;假设农户群体选择合作策略的概率为y(y∈0,1),选择不合作策略的概率为1-y。
政府选择补偿政策(A)与不补偿政策(B)的期望收益分别为u1A、u1B,平均期望收益为1,则有:
u1A=yω-S-θσ+μ+1-yω-θσ(1)
u1B=yω-θσ+μ+1-yω-θσ-ρ(2)
1=xu1A+1-xu1B(3)
农户选择合作策略(C)与不合作策略(D)的期望收益分别为u1C、u1D,平均期望收益为2,则有:
u1C=xB0+S+B1-C+1-xB0+B1-C(4)
u1D=xB0-D+1-xB0-D(5)
2=yu1C+1-yu1D(6)
根据复制动态方程原理,由博弈方策略变化率等于微分方程,可演算博弈方演化稳定策略(ESS)的复制动态方程,得到地方政府采取生态补偿政策的复制动态方程:
Fx=dxdt=xu1A-1=x1-x-S+ρy+ρ(7)
同理,得到农户群体采取合作提升流域氮素流通效率策略的复制动态方程:
Fy=dydt=yu1C-2=y1-ySx+B1-C+D(8)
联立方程(7),(8),得到基于流域氮素流通效率提升的政府与农户的二维动态博弈系统(I):
Fx=x1-x-S+ρy+ρFy=y1-ySx+B1-C+D(9)
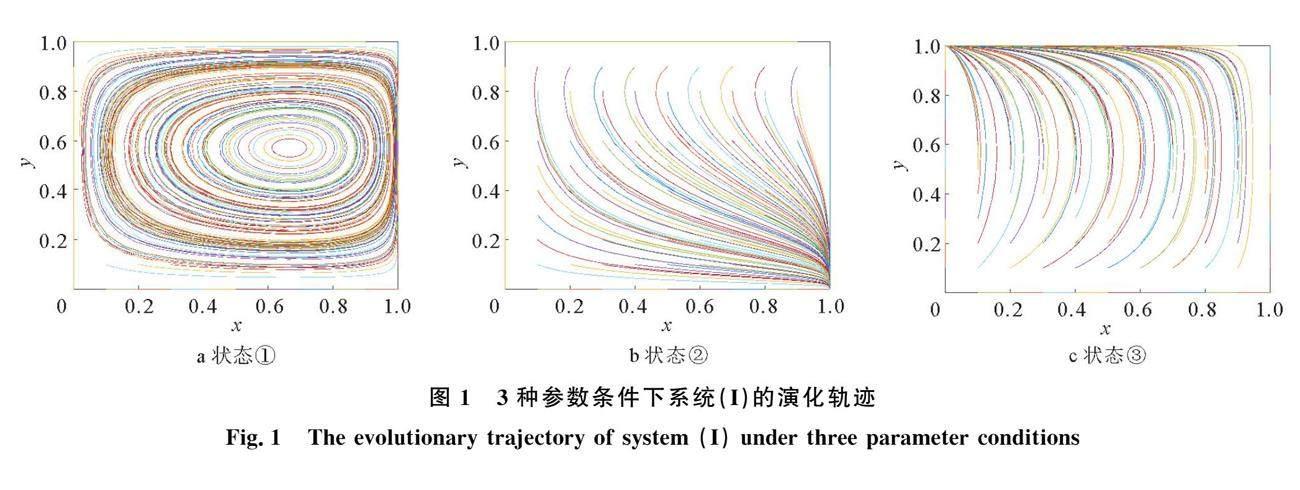
令F(x)=0,F(y)=0,得到博弈系统(I)的5个演化均衡点:E0=0,0,E1=1,0,E2=0,1,E3=1,1,E4=x*,y*,其中当-S 2 仿真模拟 2.1 不同参数条件下系统(I)的演化轨迹图 用MATLAB R2020b软件进行仿真分析,对演化均衡点的稳定性分析结果进行验证。分别模拟博弈系统 (I)的3种状态对各变量参数进行赋值,如表3所示。 模拟不同参数条件下二维动态系统(I)的演化轨迹图,如图1所示。 2.2 状态①下系统演化轨迹分析 如演化轨迹图1a所示,当-S 由图2a可知,x的运动轨迹围绕中心点呈现周期性波动,且整体波动幅度随着x初始值的增大而减小; 由图2b可知,y的运动轨迹也围绕中心点呈现周期性波动,且波动幅度与y的初始值呈负相关关系。因此政府与农户均不能达到稳定的演化策略,博弈系统的演化轨迹围绕中心点呈现周期性波动。 2.3 状态②下系统演化轨迹分析 如演化轨迹图1b所示,当B1-C+D<-S时,E1(1,0)为稳定演化策略,此时农户会倾向于选择不合作,政府倾向于选择补偿。 由图3a可知,政府的策略选择演化到补偿(A)的速率与y初始值呈负相关关系,并且当y初始值较大时,演化轨迹会先降低至极小值再上升,直至收敛到1即政府选择补偿;由图3b可知,农户的策略选择演化到不合作(D)的速率随x初始值的增大而加快,y最终收敛至0,即农户选择不合作。 2.4 状态③下系统演化轨迹分析 如演化轨迹图1c所示,当B1-C+D>0时,E2(0,1)为稳定演化策略。此时农户会倾向于选择合作,政府会倾向于选择不补偿。 由图4a可知,政府的策略选择演化到不补偿的速率随y初始值的增大而加快,并且当y的初始值比x大时,x会首先达到一个极大值后再下降并最终收敛至0,即政府选择不补偿;由图4b可知,农户的策略选择演化到合作的速率随x初始值的增大而加快,y最终收敛至0。此时双方都将达到利益最大化的目标,且政府选择生态补偿策略的初始概率较大时,农户会更快参与合作。 3 动态生态补偿政策下的演化博弈模型 3.1 系统均衡点稳定性分析 为进一步探索生态补偿的实践方式,基于政策执行的实际绩效长期调控,政府可以选择采用动态生态补偿政策,生态补偿标准与合作的农户群体比例成反比。因此,在地方政府选择生态补偿策略(A),农户选择积极合作策略(C)时,农户生产达标得到的生态补偿收益为(1-y)S* ,其中S*为政府给予农户的生态补偿上限。计算新的动态复制方程,得到地方政府与农户的二维动态博弈系统(Ⅱ): Fx=x1-x-1-yS*+ρy+ρ F(y)=y1-y[(1-y)S*x+B1-C+D](11) 令Fx=0,Fy=0,求解得到博弈系统(Ⅱ)的5个演化均衡点:e0=0,0,e1=1,0,e2=0,1,e3=1,1,e4=x**,y**,其中x**=-(B1-C+D)S*-ρ,y**=ρS*,则当0<ρS*<1,ρ-S* J'=1-2x-1-yS*+ρy+ρ x1-x2y-1S*+ρ y1-y2S* 1-2y1-y3y-1S*x+B1-C+D(12) 将演化均衡点e0,e1,e2,e3分别代入对应Jacobian矩阵的行列式与迹,得到e0,e1,e2,e3皆为鞍点;将e4带入对应Jacobian矩阵,求解特征根得到:λ1,λ2=(S*x**/2± Δ)(y**-1),为一对具有负实部的特征复根,则e4为演化博弈系统(Ⅱ)的稳定均衡点。 综上可知,就地方政府而言,选择采取降低技术成本C、生态补偿上限S*和提高额外收益B1、生态环境损害D、社会舆论成本ρ的措施都会降低地方政府选择生态补偿政策的概率,减少监管部门付出的成本,提高行政效率;就农户群体而言,选择采取降低生态补偿上限S*和提高社会舆论成本ρ的措施都可以有效增大农户积极合作的群体比例。 3.3 仿真模拟 取参数值B1=1,C=4,D=2.9,ρ=2,S*=2.5,得到均衡解x**=0.2,y**=0.8。用MATLAB R2020b软件进行仿真分析,二维动态系统(Ⅱ)的演化轨迹图如图5所示。 由系统(Ⅱ)的演化轨迹图可知,系统的演化轨迹围绕均衡点呈螺旋式结构,最终将收敛于混合策略焦点e40.2,0.8。x,y取不同的初始值,分别模拟地方政府与农户群体策略选择的演化过程,如图6所示。 由图6可知,无论x,y取何初始值,政府与农户最终达到的博弈均衡点中,双方主体策略选择的概率是固定的。因此,动态生态补偿政策下系统的演化结果更为稳定。 3.4 关键参数对演化结果的影响分析 为探讨主要参数对均衡解的影响,x**和y**的初始值皆取0.5,模拟系统(Ⅱ)混合策略焦点与演化轨迹的变化情况,如图7所示。1)农户的综合生产收益B1-C+D对演化结果的影响分析。如图7a所示,B1-C+D初始值降至0.15时,新的混合策略焦点为e'40.3,0.8,政府群体选择补偿政策的比例增大,农户群体选择合作策略的比例不变。若流域水环境与农村生产环境改善能为农户带来更多生产收益时,政府的监督压力将减轻;然而由于补偿标准未改变,农民的生产收益没有受到生态补偿政策的直接影响,其参与调整耕作措施的意愿程度未发生变化。2)政府给予积极合作农户的生态补偿上限S*对演化结果的影响分析。如图7b所示,S*初始值升至3时,新的混合策略焦点为e″40.1,0.667,最终政府选择补偿的比例和农户选择合作的比例都會减小。若初始生态补偿上限过高,尽管政策执行初期农户积极性有所提升,但随着系统演化至稳定策略,农户的合作比例趋于稳定。因此,适当降低生态补偿上限S*,虽然要求政府及时监测农户行为,不断调整动态补贴调整机制,但能有效提升农户选择合作的比例,提升氮素流通效率。3)政府承担的社会舆论成本ρ对演化结果的影响分析。如图7c所示,ρ初始值降至1时,新的混合策略焦点为e″′40.067,0.4,最终政府选择补偿的比例和农户选择合作的比例都会减小。因此,社会舆论成本ρ的增大将有效促使政府增强监管力度,推动实施生态补偿政策。由此可见,在现实的生态补偿政策执行过程中,充分发挥舆论监督作用,能够一定程度上避免监管体系不完善、信息不对称等障碍造成农户逆向选择的风险。 4 结论与建议 4.1 研究结论 本文基于流域氮素效率提升建立有限理性地方政府与农户的生态补偿演化博弈模型,分别探讨静态与动态补偿机制下博弈系统的演化稳定策略,对均衡点进行稳定性分析,仿真模拟博弈系统演化轨迹,最后分析主要参数对系统演化的影响,得出如下结论:静态生态补偿政策下,系统演化轨迹共存在3种情况,其中最贴合实际的情况下,农户决策演化的运动轨迹呈现周期性波动,且波动幅度与合作比例的初始值呈负相关;动态政策下,双方策略选择的演化结果更为稳定,博弈系统的演化轨迹螺旋式趋近于混合策略焦点,此时适当控制生态补偿上限,可增大农户积极合作的比例,发挥舆论监督作用,能够提升农户对政策绩效的满意度,加快双方达到稳定策略的博弈速率。 4.2 政策建议 1)应结合实际情况选择静态或动态的生态补偿政策。静态政策下,为减轻农户决策波动的不稳定性,规避农户道德风险与逆向选择等问题,政府应重点考虑在初期增强政策执行强度,采取技术宣传等措施增大农户的初始合作比例。动态政策下,政府应充分发挥外源激励的调节作用,需根据实际绩效与农户的响应情况进行长期调控,不断完善生态政策,合理调整补偿上限,提升农户调整耕作措施的合作意愿。 2)应增强农户调整生产方式的内生动力,大力提倡科技兴农战略,提高农业技术水平,完善健全农业技术推广机制。政府应发展因土施肥等技术,提供必要的技术指导与宣传教育,减轻从众的习惯性生产行为。有效的内源激励手段能促使农户主动转变生产方式,对于鼓励农户合作具有长期性与根本性的影响。 3)应充分发挥舆论监督作用,全面提升社会公众的参与度。政府应主动接受社会监督,细化和公开资金流向,提升生态补偿政策透明度,增强农户对外源激励政策绩效的满意程度,尽量避免监管体系不完善、信息不全面等障碍因素,规避农户道德风险与逆向选择问题。 参考文献: [1]朱德米.构建流域水污染防治的跨部门合作机制——以太湖流域为例[J].中国行政管理,2009(4):86-91. ZHU D M. Building a cross-sectoral cooperation mechanism for water pollution prevention and control in river basins—Taihu Lake Basin as an example[J]. China Administrative Management,2009(4):86-91. [2]徐昌城,曾悦.氮足迹模型应用进展研究[J].环境科学与管理,2016,41(8):47-51. XU C C , ZENG Y. Research on the progress of nitrogen footprint model application[J]. Environmental Science and Management,2016,41(8):47-51. [3]李春喜,刘晴.有机物料还田和减施氮肥对麦-玉周年农田碳氮水足迹及经济效益的影响[J].农业资源与环境学报,2020,37(4):527-536. LI C X , LIU Q. Effects of organic material return and nitrogen fertilizer reduction on carbon, nitrogen and water footprint and economic benefits of wheat-yu annual farmland[J]. Journal of Agricultural Resources and Environment,2020,37(4):527-536. [4]赖敏,王伟力.社会经济系统氮素流动及其环境负荷——以长江中下游城市群为例[J].中国人口·资源与环境,2015,25(12):15-24. LAI M, WANG W L. Nitrogen flow of socio-economic system and its environmental load—a case study of urban cluster in the middle and lower reaches of Yangtze River[J]. China Population-Resources and Environment,2015,25(12):15-24. [5]Ozanne A, Hogan T, Colman D. Moral hazard, Risk aversion and compliance monitoring in agri‐environmental policy[J]. Eur Rev Agric Econ, 2001, 28(3): 329-347. [6]Kelley H, Rensburg T, Yadav L. A micro-simulation evaluation of the effectiveness of an Irish grass roots agri-environmental scheme[J]. Land Use Policy, 2013, 31(5):182-195. [7]蔡銀莺,张安录.规划管制下农田生态补偿的研究进展分析[J].自然资源学报,2010,25(5):868-880. CAI Y Y, ZHANG A L . Analysis of research progress on ecological compensation of farmland under planning control[J]. Journal of Natural Resources,2010,25(5):868-880. [8]吕悦风.基于化肥施用控制的稻田生态补偿标准研究—以南京市溧水区为例[J].生态学报,2019,39(1):63-72. LV Y F . Research on ecological compensation criteria for paddy fields based on fertilizer application control: an example from Lishui District, Nanjing[J]. Journal of Ecology,2019,39(1):63-72. [9]焦建玲,陳洁,李兰兰.碳减排奖惩机制下地方政府和企业行为演化博弈分析[J].中国管理科学,2017,25(10):140-150. JIAO J L , CHEN J, LI L L. Game analysis of the evolution of local government and enterprise behavior under carbon emission reduction reward and punishment mechanism[J]. China Management Science,2017,25(10):140-150. [10] 徐大伟,涂少云.基于演化博弈的流域生态补偿利益冲突分析[J].中国人口·资源与环境,2012,22(2):8-14. XU D W , TU S Y. Analysis of conflicting interests in watershed ecological compensation based on evolutionary game[J]. China Population-Resources and Environment,2012,22(2):8-14. [11] 李昌峰,张娈英.基于演化博弈理论的流域生态补偿研究—以太湖流域为例[J].中国人口·资源与环境,2014,24(1):171-176. LI C F, ZHANG M Y. Research on ecological compensation in watersheds based on evolutionary game theory—Taihu Lake watershed as an example[J]. China Population-Resources and Environment,2014,24(1):171-176. [12] 付秋芳, 忻莉燕, 马士华. 惩罚机制下供应链企业碳减排投入的演化博弈[J]. 管理科学学报, 2016, 3(4):56-70. FU Q F, XIN L Y, MA S H. The evolutionary game of carbon emission reduction input of supply chain enterprises under penalty mechanism[J]. Journal of Management Science, 2016, 3(4):56-70. [13] 崔浩, 陈晓剑, 张道武. 共同治理结构下企业所有权配置的进化博弈分析[J]. 运筹与管理, 2004, 7(6):64-68. CUI H, CHEN X J, ZHANG D W. Evolutionary game analysis of corporate ownership allocation under shared governance structure[J]. Operations Research and Management, 2004, 7(6):64-68. (责任编辑 耿金花)
