下肢微重力模拟外骨骼系统的研究
2023-04-26吴岳桥梁国星李志利戴小倩李文炯刘书娟张剑峰
吴岳桥, 梁国星, 李志利 , 戴小倩, 李文炯, 刘书娟, 张剑峰
(1.太原理工大学机械与运载工程学院, 太原 030024; 2.中国航天员科研训练中心航天医学基础与应用国家重点实验室, 北京 100094)
1 引言
长期载人航天飞行过程中,太空微重力环境会对人体的心血管系统、骨骼肌肉系统等产生多种不良影响,影响航天员在轨健康和安全[1]。为确保航天员在太空的安全健康和任务的顺利完成,国内外航天机构研究建立了多种地面微重力环境模拟方法与系统,用于开展科学研究和航天员训练。例如:抛物线飞行法、落塔法、气浮法、水浮法、悬吊法以及外骨骼法,其中悬吊法出现的时间较早,是一种成熟且应用广泛的模拟方法。外骨骼法是一种新型的微重力模拟方法,目前仍在探索研究,尚未成熟应用。
悬吊法可分为斜面悬吊法和垂直悬吊法。垂直悬吊法是通过竖直悬吊人体躯干降低足底压力,从而达到模拟微重力的足底力学效果。该类系统具有操作简单、易于实施和维护的优点[2-3],但是该类型系统无法补偿人体四肢的重力载荷,受试者运动时肩、肘、髋、膝等大关节仍承受着1 G 的重力,系统无法模拟四肢的微重力环境受力状态。
外骨骼法利用被动重力平衡技术平衡人体的重力,其突出优点是能够模拟人体四肢的微重力环境受力状态[4-5]。被动重力平衡技术是指利用机械装置平衡目标系统的重力,而不使用任何的动力组件和控制系统。在外骨骼法系统中,用于平衡人体四肢重力的外骨骼属于串联机器人,其常用的被动重力平衡方法有配重法、纯弹簧法和弹簧机构法[6-8]。配重法是通过添加等量的配重,使机械臂的质心位置保持不变,实现机器人的重力平衡。采用配重法的系统,运动时会产生较大的惯性力,影响微重力环境模拟效果,因此该方法不适合应用于微重力环境模拟系统。纯弹簧法是通过在机械臂的适当位置添加弹簧,依靠弹簧力耦合实现机器人的重力平衡。纯弹簧法具有惯性小、结构简单的优点,新墨西哥州立大学和南京航空航天大学研究建立的微重力环境模拟系统,都采用了纯弹簧法补偿人体下肢重力。系统通过协同调整弹簧的安装位置和弹性系数,实现对重力补偿水平的调节控制[9-11]。弹簧机构法可分为凸轮机构法、齿轮机构法和辅助杆件法,三者的共同原理是通过弹簧机构运动调节弹簧的变形量,从而精确平衡机器人的重力。弹簧机构法的设计难度较大且安装精度要求高,但同时也具有调节精度高、易于调控等优点[12-13]。
本文选择采用弹簧机构法补偿人体下肢的重力,设计了一种带有辅助杆件的下肢外骨骼系统,用于解决垂直悬吊式系统无法补偿人体四肢重力载荷的问题,提高垂直悬吊式系统的微重力环境模拟真实度。新型外骨骼通过协同调节辅助杆件的安装位置、弹簧的弹性系数和位置参数,实现对重力补偿水平的调节控制,具有调控范围大、调控方便、补偿效果好的优点。本文对所设计的系统进行了重力补偿推导计算,并从动力学角度研究分析了重力平衡对人体下肢系统动力学性能的影响。
2 外骨骼系统概念设计
2.1 外骨骼概念设计
图1 为改进后安装有下肢外骨骼系统的垂直悬吊式微重力模拟系统,主要由恒拉力悬吊系统、上身束缚系统、下肢外骨骼系统和跑步机等组成。图2 为带有辅助杆件的新型下肢微重力模拟外骨骼系统。下肢外骨骼由腰部连杆、大腿杆、小腿杆、辅助连杆、髋关节、膝关节和弹簧组成,所有连杆均为伸缩杆,可根据佩戴者腿部的几何形状和惯性参数进行调节。辅助连杆将2 根弹簧的张力转换为髋关节和膝关节的平衡扭矩,以克服重力的影响。通过调节弹簧辅助杆件机构,实现任意重力补偿水平的精确调节控制,满足不同体重的受试者,模拟不同微重力环境状态。下肢外骨骼在踝关节之前结束,对踝关节没有限制,髋关节有2 个自由度、膝关节有1 个自由度,能够实现髋关节的屈伸、外展、内收和膝关节的屈伸[12-14]。
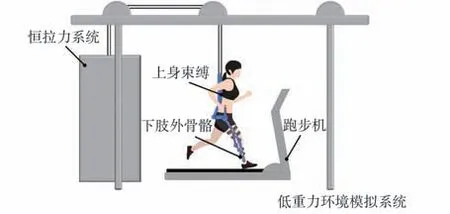
图1 微重力模拟系统示意图Fig.1 Schematics of low gravity simulation system
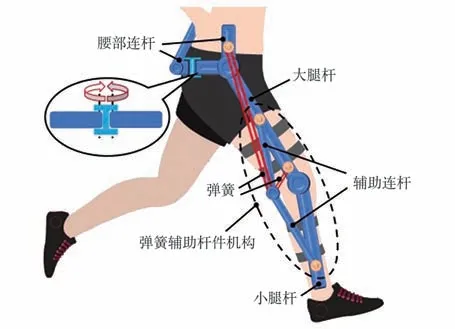
图2 被动外骨骼概念设计图Fig.2 Conceptual design of passive exoskeleton
2.2 重力补偿原理
被动重力平衡的设计主要有力矩对等和能量守恒2 种方式[4-7],本文选择能量守恒的方法以过髋关节的水平面为零势能面。由外骨骼和人体下肢组成的人机系统,其重力势能会随着髋关节和膝关节角度变化而变化,弹簧的作用是使系统的重力势能和弹簧的弹性势能相互转换,系统的总势能在任意位姿保持恒定。当人机系统总势能保持不变时,系统处于重力平衡状态,人体下肢重力得到补偿,其数学表达式见式(1)。
式中,UToal、ULG、UMG、US分别表示系统总势能、人体下肢重力势能、机构重力势能、弹簧弹性势能。式(1)表示完全补偿重力的失重状态,如果需要模拟月球、火星等微重力状态,则如式(2)所示:
式中,ρ为比例系数,表示被补偿的下肢重力与原始下肢重力的比值。例如,月球的重力是地球重力的1/6,因此模拟月球的微重力环境时,需要平衡5/6 的重力,此时ρ为5/6。
3 重力平衡计算
系统重力平衡设计的关键在于如何确定弹簧的参数和安装位置。本文基于能量守恒使用刚度矩阵法[15-16]推导重力补偿被动外骨骼的设计公式,确定弹簧辅助杆件机构的几何参数。下肢系统数学模型如图3 所示。
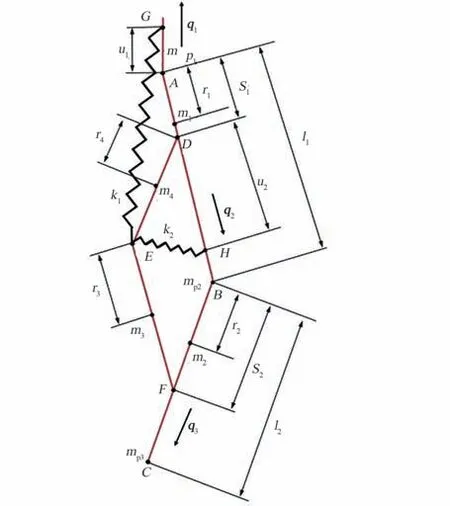
图3 下肢人机系统数学模型Fig.3 Mathematical model of lower limb man-machine system
图中,m1、m2、m3、m4分别表示大腿段AB(大腿和大腿连杆)、小腿段BC(小腿和小腿连杆)、辅助连杆DE、辅助连杆EF的质量。mp1、mp2分别表示髋关节A、膝关节B的质量,mp3表示踝关节和脚的质量。l1、l2分别表示大腿段AB、小腿段BC的长度。s1表示髋关节A到铰接点D的距离,s2表示膝关节B到铰接点F的距离。r1表示大腿段的质心到髋关节A的距离,r2表示小腿段质心到膝关节B的距离,r3表示辅助连杆EF质心到铰接点E的距离,r4表示辅助连杆DE的质心到铰接点D的距离。k1、k2表示2 个弹簧的弹性系数,u1表示弹簧k1连接点G到髋关节A的距离,u2表示表弹簧k2连接点H到铰接点D的距离。q1表示沿连杆AG的单位方向向量,q2表示沿连杆AB的单位方向向量,q3表示沿连杆BC的单位方向向量。
首先计算系统重力势能的刚度矩阵,整个系统的质心向量如式(3)所示。
式中,M表示系统总质量,C表系统的质心向量,C可表示为式(4)。

式中,K2∈R6×6为分块矩阵,I为2× 2 的单位矩阵,K2即为系统弹性势能的刚度矩阵。最后计算系统总势能的刚度矩阵,根据式(5)、(7)系统的总势能可表示为式(9)。
K即为系统总势能的刚度矩阵,当刚度矩阵的非对角线分量全为零时,系统总势能守恒系统处于重力平衡状态[6,15-16],如式(10)所示。
由式(10)可知,设计方程中的变量有辅助杆件的安装位置u1、u2,弹簧的弹性系数k1、k2以及位置参数s1、s2。由于在实际应用中很难获取特定弹性系数的弹簧,因此可以通过协同调节辅助连杆的安装位置、弹簧的弹性系数和位置参数,满足不同体重的受试者和模拟不同微重力环境状态的需求。
4 动力学分析
下肢系统属于多关节空间连杆机构,故将系统简化为多连杆模型。下肢的运动主要集中于矢状面内,为了方便计算在建模时只考虑在矢状面内的运动,忽略下肢在额状面和水平面的运动。下肢运动的一个步态周期可分为支撑相和摆动相2 个阶段,由于本文主要目的是研究重力补偿对系统动力学性能的影响,因此本文只建立单腿支撑的摆动相动力学模型[17-18]。图4 为矢状面内摆动相阶段的多连杆动力学模型。
图4 中,θ1表示大腿段AB与竖直方向的夹角,θ2表示大腿段AB与小腿段BF的夹角,Q1、Q2分别表示髋关节A、膝关节B的关节力矩,其余参数与前文数学模型参数定义相同。利用拉格朗日方程进行动力学分析,下肢系统连杆模型的拉格朗日方程为式(11)。
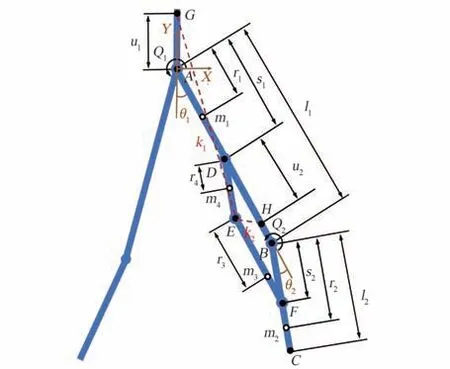
图4 下肢人机系统动力学模型Fig.4 Dynamic model of lower limb man-machine system
式中,EK表示人机系统总动能,EP表示人机系统的总势能,计算各连杆质心的位置和速度。
杆AB的质心坐标(x1,y1) 为式(12)。

将式 (14)、(15)代入式(11)整理得系统的拉格朗日方程。根据拉格朗日方程,计算下肢系统的动力学方程,系统动力学方程为式(16)。

将式(17)、(18)代入式(16)中,整理可得人机系统髋关节和膝关节的关节力矩,为了方便研究分析将结果写成矩阵形式,如式(19)。


分析计算结果可知,关节力矩与重力项矩阵和弹力项矩阵有关,选择合适的弹簧参数能够抵消或者减小重力项矩阵,从而减小髋关节和膝关节的关节力矩,实现人体下肢的微重力环境模拟。
5 仿真验证
根据国家标准GB/T17245-2004《成年人人体惯性参数》和GB 1000-88《中国成年人人体尺寸》确定人体下肢和外骨骼的几何和惯性参数。根据上文推导的设计公式(10)确定弹簧辅助杆件机构的几何参数。在动力学建模的基础上利用三维建模软件SOLIDWORKS 构建人机系统下肢模型,并将建立好的模型导入ADAMS 中添加约束,不添加关节驱动,设置系统重力为9.8 N/kg,设置模型的参数见表1,设置仿真时间为10 s,step步数为1000 步。将仿真模型初始位姿设置为提膝状态,仿真验证外骨骼系统能否平衡下肢重力,仿真结果如图5 所示。

表1 系统参数表Table 1 Values of system parameters
图5 中,虚线代表未添加弹簧时的仿真结果,实线代表添加弹簧时的仿真结果。结果表明,在未添加弹簧力时,受重力影响各部分的质心位置会发生变化,模型无法在重力场中保持原始位姿状态,在添加弹簧力时,各部分的质心位置保持静止,下肢所受重力得到精确补偿,模型能在重力场中保持平衡状态,证明外骨骼系统系统能够平衡下肢重力。
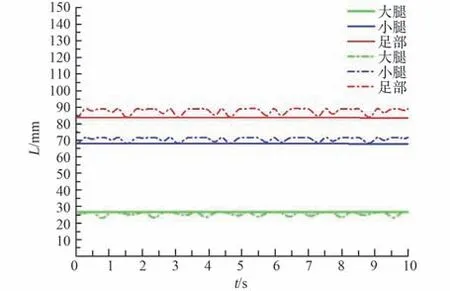
图5 质心位置变化曲线Fig.5 Change curve of centroid position
依据文献[19],确定髋关节和膝关节在一个步态周期内的角度变化曲线。利用ADAMS 的STEP 函数编写髋关节和膝关节的驱动函数,设置系统重力为9.8 N/kg,设置仿真时间为5 s,step步数为500 步。
图6 为模拟不同重力环境下,下肢摆动时髋关节和膝关节的关节力矩变换曲线,图6(a)代表未平衡系统重力,模拟地球重力环境的仿真结果,图6(b)代表平衡系统部分重力,模拟月球和火星低重环境的仿真结果,图6(c)代表平衡系统全部重力,模拟太空失重环境的仿真结果。结果表明,随着重力补偿水平即弹簧力的不断增加,下肢的关节力矩逐渐减小,证明弹簧弹力补偿了下肢重力,减小或消除了重力对下肢运动的影响,与本文动力学分析结果具有一致性。并且仿真结果证明在外骨骼模拟的低重力环境和实际低重力环境中下肢运动的生物力学特性具有相似性,外骨骼能够模拟真实低重力环境[10,17-18]。
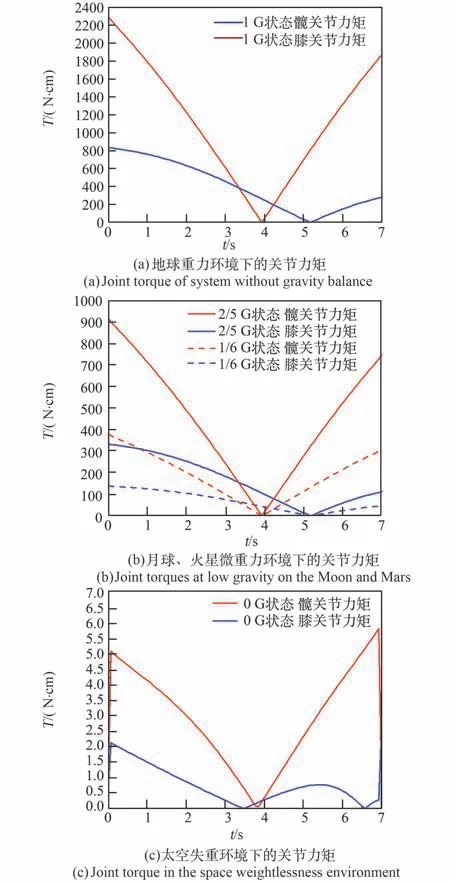
图6 系统关节力矩变化曲线Fig.6 Curve of system joint torque
图7 为失重状态下,系统势能的变化曲线,结果表明,在仿真运动过程中,系统的重力势能不断下降,弹性势能在不断上升,系统的总势能保持恒定不变,证明能够实现重力势能和弹性之间的相互转换,维持系统的总势能保持不变[20],结果与本文重力补偿原理一致,验证了重力补偿原理的可行性和设计公式的正确性。
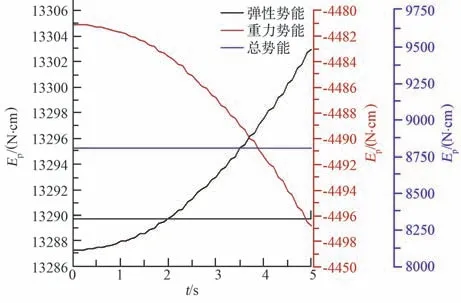
图7 系统势能变化曲线Fig.7 Curve of system potential energy
6 结论
本文针对悬吊式微重力环境模拟系统无法模拟人体下肢低重力环境的问题,提出利用外骨骼机器人模拟下肢低重力环境的解决方案。采用被动重力平衡的方法设计了外骨骼,以实现模拟下肢的低重力环境受力状态,并利用刚度矩阵法对重力平衡条件进行了推导,得到了外骨骼机器人重力补偿设计公式。通过数学分析和计算机仿真对外骨骼的重力补偿设计方案和设计公式的有效性和正确性进行验证。结果表明,采用弹簧辅助杆件法设计的外骨骼能够模拟下肢低重力环境。
