融合神经网络及麻雀算法的机器人避障研究

2023-04-26朱金坛

计算机测量与控制 2023年4期

朱金坛

(西安铁路职业技术学院电子信息学院，西安 710014)

0 引言

机器人自主运行的核心技术就是能避开障碍，具体来说是指机器人在无人干预的情况下，自主实现计划中要求的各点间可行路径的搜索与运行。规划过程需要结合自身运行动力特性和环境约束，根据自身能耗和速度特征，考虑环境威胁等条件，自主规划出最优路径。其中，路径的平滑度、行程长短、机器人能量消耗则是对该条路径优劣的评估标准。从规划环境尺度角度可分为全局避障和局部避障两大类。局部路径避障通过传感器获取环境数据，选择一条当下节点至下一节点的子路径，常用方法有滚动窗口法[1]、Dijkstra算法[2]、人工势场法[3]等。全局避障指在掌握运动环境的前提下，利用算法自主生成优化路径，如基于栅格图对环境建模的方法[4]、利用可视图法模拟实际环境的方式[5]以及基于open表的A*算法[6]等。

上述传统算法虽然容易实现，但存在实时性差、适用范围小、复杂环境计算量过大的问题。近年群智能算法的研究发展为解决机器人避障问题提供了更多解决方案。如：游达章[7]等人融合粒子群与灰狼算法，引入量子协同改善了算法在处理路径规划问题的精度；周晟[8]等人引入随机分形自适应搜索策略优化了仓储机器人多障碍多目标环境的的路径规划问题；潘纹[9]基于动态步长果蝇算法研究了自动导引车的路径规划问题。还有其他如天牛须算法[10]、鲸鱼优化算法[11]等仿生群体算法也都开始用于路径规划与避障研究当中。2020年薛建凯等[12]首次提出麻雀搜索算法，算法主要以数学公式模拟麻雀群体觅食过程，具有速度快、精度高的特点。但由于收敛速度快也更容易提早收敛于局部极值点而无法跳出、初始种群分布不够广泛以及平衡能力差等缺点。该算法在CT图检测[13]、电池参数优化[14]、算法参数优化[15]和成像偏移预测[16]等实际问题。但SSA仍存在过度依赖初始种群，收敛前种群多样性不足，易陷入局部极值且无法跳出等不足。

为解决以上问题，许多相关研究针对不同角度进行了优化改进。如G.Liu等人[17]引入混沌策略增加多样性，使用权重和突变策略加快寻优。欧阳城添等人[18]融合折射学习，以此初始化种群，丰富多样性，同时引入疯狂算子使得算法寻优能力得以提升。这些算法虽也有一些算法上的提升，但并没有从根本优化寻优机制，而是把结果交给不确定性较大的混沌随机机制，也没有考虑局部与全局的平衡，需要以时间复杂度为代价去优化算法性能。

因此针对算法提早收敛于局部、初始种群分布不够广泛和平衡能力差等问题，提出一种融合神经网络的改进麻雀搜索算法。首先，通过神经网络对规划环境进行栅格化建模，其次引入低差异的Halton序列进行麻雀种群初始化，可使得初代种群分布广泛且均匀，有很好的遍历性；再次，采用布朗运动步长策略优化传统SSA算法平衡能力差的缺陷，实现前期全局过程搜索范围广，中后期搜索精度高的平衡与切换，同时可通过布朗运动步长跳出局部收敛；最后，为了避免机器人实际运行过程出现急转急停问题，引入clothoid曲线法进行最终的路径平滑，避免了尖锐拐弯，减少实际运行时轮轴磨损和能耗。将综合改进后的算法与原始算法进行时间复杂度对比，并使用6种函数对几种常见算法进行横向对比，最后将改进后算法与SSA算法和CSSA算法[19]进行不同尺度的环境规划对比，综合评价算法的机器人避障效果指标性能。

1 麻雀搜索算法

麻雀搜索算法(SSA)是一种启发式算法，由麻雀搜索食物过程中的行为模式启发而来，有算法稳定、寻优速度较快的特点。不仅优于传统粒子群算法，对于新型的算法如灰狼算法、引力搜索算法也具有一定优势。SSA真个种群共有3种角色，分别是发现者、尾随者和警戒者，三者有不同的任务分工，发现者负责探索食物方位，并将食物位置共享给跟随者，跟随者的任务则是尾随发现者，当收到发现者的位置更新后，则前往新位置准备觅食，同时，为了保证种群安全，种群中部分个体会在觅食前进行警戒，当收到危险信号时则会通知种群放弃觅食。

对于算法而言，发现者即执行的全局探测任务，跟随者即对更新的位置信息进行局部寻优，当陷入局部极小值时，有警戒者负责释放危险信号跳出局部，重新进行全局寻优。具有预警机制也是该算法优于其他算法的核心，使得SSA相较于其他算法更不易陷入局部最优解，更容易取得全局最优解。

SSA算法中的发现者、追随者以及警戒者，分别按照各自规则进行位置更新，更新规则如式(1)～(3)所示：

(1)

(2)

(3)

2 改进的麻雀搜索算法

2.1 三层神经网络建模

首先有三点假设前提：一是机器人运动范围并非无限，而是在限定范围内自主运行；二是以机器人最大尺度半径膨胀障碍物，得到栅格环境；三是将机器人视为无尺度无边界的质点处理。三层并联神经网络如图1所示，数学表达如式(4)所示：

图1 神经网络的环境建模

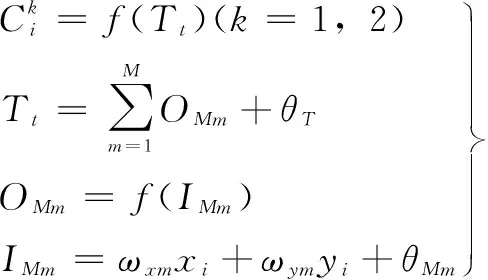
(4)

其中：θim=(i=1，2，…，8)计算路径如下：

(5)

式中，假设机器人的切线方向速度在[ti，ti+1]内不变。Vkx和Vky为速度分量。ti与ti+1之间的关系如下式：

(6)

式中，机器人在ti时速度为vrob，且在[ti，ti+1]速度不变。

(7)

式中，避碰检测值Z为0时，代表可行路径，取正值时则产生碰撞，路径不可行。障碍物数目为PR，路径等分点个数为Pe。此模型可同时计算出当前路径与所有障碍物之间的碰撞结果。

2.2 低差异序列初始化

初代种群分布的广泛性与均匀性直接影响算法收敛的速度。初代种群分布越广，全局探索的速度越快，局部寻优的精度越高。标准SSA中初代麻雀种群位置过于随机，均匀性过低、许多区域存在盲区，不够遍历。因此引入一种基于超均匀分布的均匀分布随机数组Halton序列，以此代替随机数进行种群初始化操作。

Halton序列主要有如下三步计算过程：

1)假定p≥2且为质数，对任意整数n，n∈(1，N)，可以p为基表达出如式(8)的形式：

bi∈{0，1，…，p-1}

(8)

2)已知bi与p，基本逆序函数如式(9)：

φp(n)=(0.b0b1…bm)p=b0p-1+

b1p-2+…+bmp-m-1

(9)

3)d维空间的Halton序列计算如式(10)：

H(n)=[φp1(n)，φp2(n)，…，φpd(n)]

(10)

在解空间上下限中生成一个取值范围在0和1之间的随机数Kn，初始位置Xn如式(11)所示：

Xn=Xmin+Kn·(Xmax-Xmin)

(11)

如图2所示，可以清楚看出二维空间中Halton序列相对于伪随机数法可将种群分布得更加均匀。

图2 二维位置分布对比图

由图2可看出，Halton序列初始化种群相比伪随机数序列得到分布更均匀、遍历性更广的初始化麻雀群体。

2.3 布朗运动步长策略

传统SSA算法的迭代步长由一个符合均匀分布的随机数作为步长因子，存在随机性过大的问题，不能很好的平衡前期全局开发与中后期局部开发的过程切换。因此引入布朗运动步长策略，满足前期全局过程搜索范围足够广，中后期搜索精度足够高的运行要求，当算法收敛于局部最优值，也可通过布朗运动策略跳出局部最优，脱离算法停滞。

布朗运动的步长服从均值为0方差为1的高斯分布，其本质是一个均匀可控的步长随机过程，概率密度函数如式(12)所示：

(12)

麻雀位置更新公式为：

(13)

式(13)中，布朗运动步长以RB表示；P等于1/2；R为(0，1)间随机数。

2.4 clothoid曲线法的路径平滑

clothoid曲线广泛运用于车辆行驶轨迹设计，路径规划等方向，是一种曲率半径随弧长线性变化的曲线，可以在直线段与曲线段平滑过渡。clothoid曲线的数学表达如式(14)所示：

(14)

式中，(x0，y0)为起点，θ0为切线角初始值，k为曲率，下标0代表初始值，c为曲率锐度参数，s为弧长。其中曲率k和切线角θ的计算如式(15)所示：

(15)

假设算法中关键点坐标为P(xi，yi)(i=1，2，…)上的离散点，那么对各点曲线拟合的过程，即保证曲率连续，求解k个离散点的各曲线段。图3为一组离散点经拟合后的曲线段。

图3 若干离散点拟合成clothoid曲线段

对于任意的第l段曲线，其端点坐标满足如式(16)条件：

(16)

式中，第l段弧长为sl，(x1，y1)点的切线角为θ0l，曲率为k0l。为保证各点曲率连续且平滑，各参数满足如式(17)的要求：

(17)

式中，前后两段曲线交点处切线角、曲率均前后相等。即第l+1段曲线起点切线角等于第l段曲线的终点切线角，第l+1段曲线起点曲率等于第l段曲线的终点曲率。

2.5 改进算法描述

改进后的算法流程图大致可分为初始化阶段、网络建模阶段、判断阶段和位置更新阶段，具体如图4所示。

图4 改进算法流程图

首先通过式(8)～(11)以三层神经网络对规划环境进行栅格化建模，生成膨胀后的栅格图，再对各参数初始化；用公式(4)～(6)对种群进行低差异序列初始化，形成分布均匀的种群；分别以式(1)、(3)、(7)更新尾随麻雀、警戒麻雀和发现者的位置，若果算法陷入局部最优则以布朗运动步长通过式(13)跳出局部最优，若存在个体位置超过解空间上下界，也通过式(13)进行位置初始化；最后当满足设定迭代次数时，结束算法，再对路径进行平滑，同时输出平滑前后的路径，得到对应收敛曲线。

2.6 算法复杂度分析

时间复杂度反映了算法面对复杂问题的求解能力。若在D维解空间存在规模为N的初代种群，求解该问题需要消耗f(D)的时间。则时间复杂度可表示为：

T=O(D+f(D))

(18)

在一系列的改进后，初始化参数用时记为η0，各随机因子生成时间记为η1，任意一维种群产生耗时为η2，越界重置位置时间记为η3，此时的时间复杂度可表示为如下公式：

T1=O(η0+Nf(D)+D(η1+η2+η3))=

O(D+f(D))

(19)

种群存在不同类型个体。发现者有r1N个，r1即发现者在种群所有个体中的占比，任意一维位置更新耗时η4，随机因子生成需消耗时长η5，则发现者执行阶段时间复杂度可表示为：

T2=O(r1N(η4+η5+η5)D)=O(D)

(20)

追随者有r2N，同样的r2为其在个体总量的占比，任意一维位置更新耗时η6，随机因子消耗时长η7，则追随者执行阶段时间复杂度可表示为：

T3=O(r2N(η6+η7)D)=O(D)

(21)

除去发现者与追随者，剩余的均为警戒者，数量则为(1-r1-r2)N，任一维位置更新耗时η8，随机因子消耗时长为η9，则警戒者执行阶段时间复杂度可表示为：

T4=O((1-r1-r2)N(η8+η9+η9)D)=O(D)

(22)

在布朗运动阶段，按式(13)更新麻雀最优个体所需的时间为η10，生成随机步长R所需的时间分别为η11，则此阶段的时间复杂度为：

T5=O(N(η10+η11+η12)D)=O(D)

(23)

最大迭代次数为itermax，改进算法的时间复杂度为：

T′=T1+itermax(T2+T3+T4+T5)=

O(D+f(D))

(24)

通过对比可知，算法改进前后的时间复杂度在同一水平尺度，优化改进得到的性能优化没有导致时间复杂度的额外增加。

3 仿真及分析

3.1 算法性能测试

选取2个单峰，3个复杂多峰，1个定维函数来测试算法寻优性能，具体函数如表1所示。同时将标准SSA，GWO和粒子群算法也加入一起作为横向对比，将文献[20]中的ISSA与文献[21]中的CSSA进行纵向对比，以此突出本文改进算法的新颖性与优越性。对比算法种群数量统一为100，迭代次数为500，粒子群算法中的独有参数c1=c2=2，w=0.728。统计各算法的平均值指标，并将各算法最终指标进行排序，根据排序先后衡量算法的寻优能力的强弱。表2中可以发现，改进算法对各函数均表现出较强的寻优能力，特别是在F3～F6中，改进算法的寻优效果显著。为避免均值指标的片面性，引入Wilcoxon秩检验，在5%的显著水平下进行试验，当P≤0.05时，则存在显著性差异。反之当P>0.05时，则表示差异不显著，用N/A表示，具体结果如表1所示。由表1中看出，改进算法与其他各算法存在显著差异，改进算法更具有快速处理复杂问题的优势。

表1 测试函数表

表2 算法寻优结果排序

表3 Wilconxon秩和检验P值

3.2 地图环境生成

用本文改进算法与传统麻雀算法、文献[19]中的CSSA算法作仿真结果对比。仿真计算机配置采用intel i7-11800H型号的CPU，GeForce RTX 3070显卡，32 GB运行内存。

本文以膨胀法将环境进行栅格化建立环境模型。每个栅格代表一个节点，每次可移动一个单元格，因此有8个移动方向，如图5所示。

图5 运动方向

通过建立两种图5所示的不同栅格环境，验证算法在不同尺度环境下的移动机器人的实际规划效果。栅格地图中，黑色部分即障碍，白色部分为可规划区域。坐标(0.5，0.5)为规划起点，坐标(19.5，19.5)和(39.5，39.5)为规划终点，在图6以灰色栅格表示，在仿真过程中黑色用1表示，白色和灰色用0表示。

图6 环境栅格图

栅格图中原点位于左下角，终点在右上角第j行k列，代号为G的栅格中心坐标为：

(25)

式中，横、纵坐标即x和y，mod为取余运算，int为求整公式。

3.3 算法参数

通过Matlab软件得到20*20与40*40栅格图，通过比较测试SSA算法、CSSA算法、本文改进算法在栅格地图上规划出的最短路径来对比改进算法的优越性。其主要参数设置如表4所示。

表4 基本参数设置

3.4 仿真分析

在环境大小为20×20的栅格地图中对3种算法进行仿真，得到的最优路径对比和收敛迭代曲线对比如图7所示。

图7 20×20地图仿真路径与收敛曲线对比图

图7中，左图为改进算法、原始算法同对比算法规划出的路径，改进算法因为引入了平滑改进，所以相对于其他两种算法没有尖锐转弯点，而原始算法则有7个尖锐转弯点，对比算法也有相应优化，只有5个尖锐转弯点。右图为3种算法的收敛曲线，原始算法迭代60次后趋于收敛，对比算法迭代52次后收敛稳定，改进算法最优，46代即收敛于最优路径。

在环境大小为40×40的栅格地图中对3种算法进行仿真，得到的最优路径对比和收敛迭代曲线对比如图8所示。

图8 40×40地图仿真路径与收敛曲线对比图

图8中，左图为改进算法、原始算法同对比算法规划出的路径，改进算法因为引入了平滑改进，所以相对于其他两种算法没有尖锐转弯点，由于地图尺度增加，环境障碍更加复杂，原始算法有8个尖锐转弯点，对比算法只有7个尖锐转弯点。右图为3种算法的收敛曲线，原始算法迭代175次后趋于收敛，对比算法迭代158次后收敛稳定，改进算法最优，139代即收敛于最优路径。

在20×20地图和40×40地图中，对比传统SSA、改进SSA和CSSA三种算法规划出的路径，传统SSA算法和CSSA算法由于没有路径平滑过程，均有较多的尖锐拐点，且收敛速度相对改进SSA算法更慢，其中传统SSA算法路径相对较长，加大了机器人不必要的能量消耗。改进SSA算法在路径长度上最短，收敛速度最快，且无尖锐拐点。具体指标对比如表5所示。

表5 指标对比

结果显示，在20×20地图环境下，改进SSA相对传统SSA算法最短路径缩短了6.07 m，降低了17.66%，收敛迭代次数减少14次约23.33%；改进SSA相对CSSA算法最短路径缩短了2.36 m，降低了7.69%，收敛迭代次数减少6次约11.54%。在40×40地图环境下，改进SSA相对传统SSA算法最短路径缩短了10.18 m，降低了15.43%，收敛迭代次数减少36次约20.57%；改进SSA相对CSSA算法最短路径缩短了4.03 m，降低了6.74%，收敛迭代次数减少19次约12.03%。

综合来看，改进SSA算法在不同尺度环境解决机器人避障问题表现均很突出，其各项性能指标均优于CSSA算法和传统SSA算法，可以以最快的速度收敛于最短平滑路径。