六轴工业机器人先验引导RRT*避障轨迹算法研究
2023-04-26徐文浩陈东生
徐文浩,陈东生
(中国工程物理研究院 机械制造工艺研究所,四川 绵阳 621900)
0 引言
随着科学技术的不断发展,机器人技术在社会各个领域得到了广泛应用[1]。六轴串联机器人具有自由度高、自动化程度高等特点,在非标自动化等运动受限、复杂危险的环境下具有高效的装配能力,故被越来越多地应用在自动化设备中,作为零件搬运、装配、焊接等工作的主体。但在复杂工作环境下,自动化机器人的避障要求也越来越突出,必须对避障轨迹进行规划。末端避障轨迹规划主要任务是根据作业任务的要求,计算出机器人一条从起始点到目标点的连续无碰撞路径,传统人工示教避障轨迹存在弊端,首先所得避障轨迹无法保障为最优轨迹,此外当现场设备环境发生变化时,需人工重新示教,工作量大且耗费时间。自动路径规划问题已吸引大量学者研究,提出了大量路径规划算法:基于搜索的A*算法[2-3]虽然搜索能力强,但需要对搜索范围进行栅格划分,对于高维状态空间的复杂路径规划计算开销大。基于建立引力斥力场的人工势场法[4-5]在局部避障中具有较好的性能,可生成光滑的轨迹,但是人工势场法存在局部极小值、无效避障、斥力过大等问题;基于智能算法的遗传算法[6-7]能够保证轨迹的搜索能力,但计算量大收敛速度慢,且存在容易陷入局部最优、搜索效率低等问题;基于随机采样路径规划方法[8]的提出,为解决高维度、复杂环境路径规划问题提供出了一种很好的解决思路。其中快速探索随机树(RRT,rapidly exploring random tree)算法[9]不需要空间栅格化,搜索能力强,十分适合应用在高维环境下,在机器人和许多其他领域得到广泛应用。但RRT算法搜索效率低、路径不稳定、无法得到最优路径。为此,Karaman等人[10]将渐进最优的思想引入RRT算法中,提出了RRT*算法。RRT*算法在RRT算法的基础上增加了父节点重选与剪枝重生成两个环节,利用这个过程实现渐进最优。但标准RRT*算法仍存在路径曲折、路径搜索慢等诸多方面的不足。国内外学者对标准RRT*算法进行了改进,D.Jonathan等人[11]针对上述问题提出Informed RRT*算法,通过缩小状态子集来简化路径搜索过程,提高了标准RRT*算法的收敛速度、减小了最终解决方案的成本、提高了找到困难通道的能力;赵盼等人[12]在路径规划层面上对标准 RRT*算法进行了优化,采用改进路径生成方式、引入转角约束、碰撞后调整等策略,改进了标准RRT*算法随机路径转角大、路径复杂等缺点,最终得到适用于超冗余度机器人路径跟随运动的末端避障轨迹规划算法;杨也等人[13]提出一种改进的RRT*算法,采用有目的设置采样点代替随机高斯采样和引进人工势场与避障策略结合的思想,有效地平衡了室内机器人路径规划算法收敛时间与最佳路径的可靠性;易驰等人[14]针对标准RRT*算法收敛速度慢和目标导向性差的问题,提出基于目标区域偏置扩展的RRT*算法,有效减少了随机树节点数量,加快了算法收敛速度;张珏等人[15]提出了一个高斯拟合平滑快速探索随机树智能算法(GFS RRT*-smart),用于全局路径规划,提高了机器人在弯道急转弯时的障碍回避性能;刘冲等人[16]提出一种基于RRT*的母线布线路径规划算法,通过引入中间点的方式改变已生成路径到随机点的扩展方式,同时在初始路径生成过程中采取贪心的优化策略,获得弯头数量最少且满足约束的路径,很好地满足母线的各项布线要求;崔春雷等人[17]提出了一种改进Bi-RRT的移动机器人路径规划算法,引入启发式搜索策略使采样过程,既可以利用目标点的位置信息又保证了算法的概率完备性,降低了搜索的盲目性,提高了搜索的效率;此外,杨莹等人[18]在RRT算法的基础上提出引入人工势场法引力分量使节点的扩展更具方向性的混合式算法,在快递分拣路径规划问题上得到突破。
本文针对六轴工业机器人装配应用场景,采用优化的RRT*算法规划自动避障路径,上述算法相较于标准RRT*算法均有一定程度的改进优化效果,但针对本文的应用场景仍然存在两点不足:1)上述算法尚缺少针对六轴工业机器人手臂避障的轨迹规划。六轴工业机器人除了要求末端路径与障碍物不发生碰撞之外,机器人各手臂轴也不能与障碍物发生碰撞;2)标准RRT*算法的随机性导致其轨迹优化能力不足,生成的路径曲折;轨迹搜素能力不足,面对条件较为苛刻的障碍物(如障碍物尺寸较大时)会出现绕不开障碍物、不能找到最终轨迹的情况,无法满足本文应用场景下的路径优化需求。
针对以上两个问题,本文提出一种先验引导RRT*算法,以标准RRT*算法为基础,融合包围盒算法思想以及先验引导思想,使算法能生成同时满足末端轨迹与机器人手臂避障需求的渐进最优末端轨迹,提高了算法的路径优化能力与路径搜索能力。
1 算法原理
本文提出的先验引导RRT*算法思想如下:1)在标准RRT*算法的基础上融入包围盒算法思想:(1)针对机器人手臂轴,采用包围盒算法计算手臂与障碍物的距离,进而判断是否发生碰撞;(2)针对机器人回转死区,为避免RRT*算法随机树生长到机器人回转死区内导致机器人末端无法到达,将回转死区设置为圆柱体包围盒区域进行碰撞检测。2)对RRT*算法随机点生成方向以及随机树生长方向进行先计算最优生长方向后引导其生长的先验引导机制,整体让树枝的生长方向更快速地避开障碍物、趋向目标点,使轨迹满足渐进最优需求。
1.1 RRT*算法原理
标准RRT*算法的具体流程如下:
1)生成随机树Tree:以起始点作为树的第一个节点Xstart,以目标点作为树的最终节点Xgoal;
2)随机树Tree的生长:在机器人的工作空间Q内,按照目标偏向思想随机生成采样点Xrand,之后搜索随机树Tree上距离Xrand最近的节点Xnear,以Xnear到Xrand的方向为方向向量按一个固定步长Step拓展长生出新的树枝节点Xnew,检测Xnear与Xnew两节点连线轨迹是否会与障碍物发生碰撞,不会则节点Xnew生长成功,否则废弃继续搜寻新的Xnew,生长成功后将其添加到随机树Tree上,同时计算其路径价值函数Cost(即从起始点Xstart到当前节点Xnew,依次累加节点间的距离而得到的路径距离);
3)父节点重选:在新节点Xnew的邻域r范围内搜索随机树Tree上的节点集合Xnear_coor,r为邻域的半径,其计算公式见式(1)。计算以节点Xnear_coor(i)作为Xnew父节点的路径价值Cost,将其与以Xnear作为父节点的路径价值进行比较。选择Cost小且无碰撞的路径作为新树枝更新Xnew的父节点与路径价值Cost;
4)剪枝重生成:遍历树节点集合Xnear_coor,若Xnear_coor(i)到Xnew的价值函数加上Xnew累计到Xstart的价值函数小于Xnear_coor(i)累计到Xstart的原价值函数,且Xnear_coor(i)与Xnew间的轨迹与障碍物不发生碰撞,则将Xnew作为Xnear_coor(i)的新父节点,同时更新价值函数Cost;
5)搜索过程迭代:重复上述过程,经过有限次的迭代,至随机树Tree生长出一个节点与目标点Xgoal之间的距离小于设定的阈值(阈值范围内无障碍物),之后下一次生长随机树Tree直接生长到Xgoal并停止搜索;
6)末端轨迹检索生成:随机树Tree生长结束后从其目标点Xgoal开始向起始点Xstar检索当前路径节点的父节点,之后父节点成为路径节点继续检索,依次迭代最终生成完整的末端避障轨迹。
(1)
式中,Step是树枝节点的固定生长步长,k是当前随机树Tree上所有节点的个数,该公式的作用是缩小后期节点Xnew周围的检索范围,避免后期出现因随机树上的节点数量过多而导致计算过程缓慢甚至卡死的情况。
1.2 RRT*算法改进
1.2.1 六轴工业机器人手臂碰撞检测
由1.1小节的标准RRT*算法原理介绍可知,标准RRT*算法在其第2)~4)步生长新树枝的过程中会进行末端轨迹与障碍物的碰撞检测,当满足无碰撞条件时新的树枝才会生长成功。本文在此基础上加入对机器人各手臂轴与障碍物的碰撞检测,对Xnear与Xnew两节点生成的末端轨迹利用机器人的逆向运动学,通过其DH参数求逆解[19]得到机器人的关节旋转角矩阵,再通过机器人的正向运动学求出其手臂各关节的齐次位姿矩阵,之后采用包围盒算法计算并判断机器人手臂在运行该段轨迹时是否会与障碍物发生碰撞,在满足机器人的末端与手臂均不会发生碰撞的情况下才会生长成新的树枝节点,否则废弃。以此过程不断迭代最终得到机器人各手臂轴与末端均不会与障碍物发生碰撞的轨迹。
机器人手臂避障:由于机器人手臂与障碍物结构复杂,难以用数学模型表达。故采用包围盒算法对其模型进行简化[20]:用体积稍大于原来模型但是自身特性简单的几何体(即包围盒)来近似地代替原复杂的几何模型对象。进而将碰撞问题抽象为简单的几何体的位置关系问题进行判断。
本文的研究对象为库卡KR600r2380六轴串联工业机器人,为了方便算法设计,需要对其模型进行合理简化:1)机器人的第一连杆只有转动,没有位移,所以不需要考虑其碰撞风险;2)机器人的第四关节轴和轴线平行,故其第三连杆与第四连杆位置关系始终保持不变,将二者视为一体;3)同2),机器人的第五连杆与机器人末端视为一体;4)机器人各连杆可由圆柱体近似包围,故采用圆柱体包围盒进行表示;5)在本文的应用场景中,机器人的第三连杆后端动力部位为安全位置,可不计入包围盒范围。最终简化后的示意图如图1所示。图中L1、L2、L3为简化后需考虑碰撞部分的机器人连杆中心线,设此部分机器人连杆的最大径向半径为RL1、RL2、RL3,根据其模型参数可得:RL1=285 mm、RL2=207 mm、RL3=125 mm。除此之外,根据机器人模型还可以得到机器人的DH参数表,详细如表1所示。

表1 KR600r2380机器人DH参数表
除了机器人的手臂外,机器人的回转死区也采用圆柱体包围盒描述,圆柱体径向半径为700 mm。

图1 机器人圆柱体包围盒模型
针对障碍物(本文涉及的障碍物为工位上的工装夹具),因为包围球可以较好地包围障碍物,故采用包围球表示障碍物。如图2所示,工装夹具为障碍物,以O为球心,Ro为半径的球面为包围球球面。
最终构成的障碍物空间如图3所示。
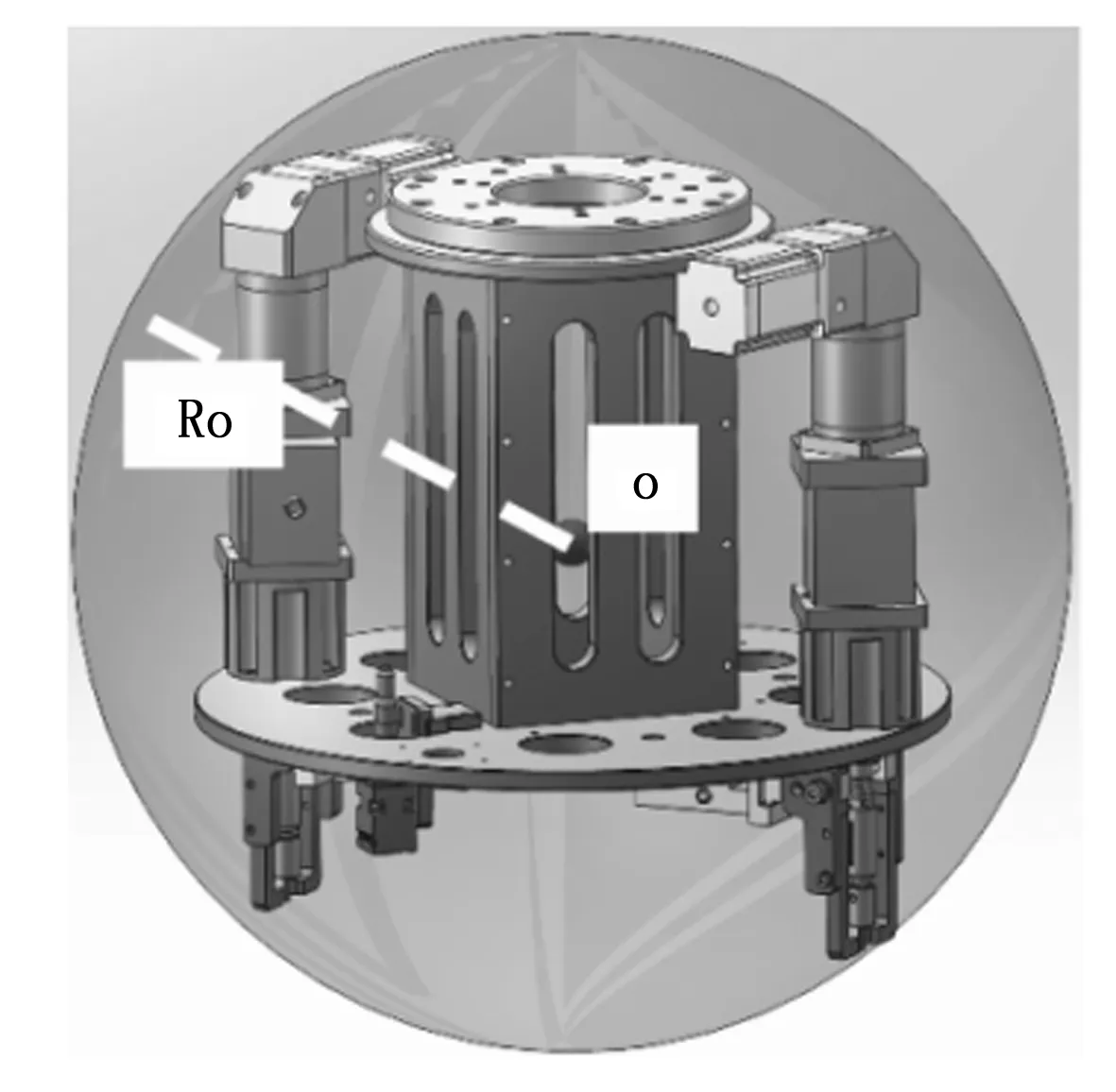
图2 障碍物包围球模型

图3 障碍物空间
最终将障碍物与机器人各手臂轴的碰撞检测转化为包围球中心到圆柱体包围盒中心线线段的距离计算。如图4所示,设包围球中心到圆柱体包围盒中心线距离为d,s为安全距离,分析可知安全距离即为包围球与圆柱体包围盒半径之和。检测机器人各手臂轴与障碍物是否发生碰撞需满足对应的计算判定结果。具体计算过程如下。
障碍物与机器人手臂的位置关系可分为两种情况,以图4中L2轴与障碍物的位置关系为例,情况a是包围球球心向圆柱体包围盒中心线的投影落在圆柱体包围盒中心线线段范围内;情况b则是其投影落在圆柱体包围盒中心线线段范围外,经归纳得,要满足机器人手臂轴与障碍物不发生碰撞仅存在两种状态,状态一是满足包围球球心到圆柱体包围盒中心线的距离d大于安全距离s,这种状态下无论是情况a还是情况b,均满足无碰撞需求。状态二是两者的距离d小于安全距离s的时候,此时需要满足两个条件才能满足无碰撞需求:条件1是包围球与圆柱体包围盒的位置关系为情况b;条件2是包围球球心到圆柱体包围盒中心线线段两端点的距离中较小者大于安全距离s。除此之外的状态机器人手臂与障碍物均会发生碰撞。故判断是否发生碰撞需分情况进行讨论。
首先计算包围球球心到圆柱体包围盒中心线的垂直距离d。通过机器人逆向运动学,根据机器人末端坐标可计算得到机器人关节角矩阵q,再由机器人正向运动学得到机器人各个关节的齐次位姿矩阵T,其中T(1,4)、T(2,4)、T(3,4)分别为机器人各关节位置的x、y、z坐标,设Ta、Tb、Tc、Td分别为机器人关节二、三、五、六的齐次位姿矩阵,由式(2)可求出对应的齐次矩阵:
(2)
进而由式(3)可求出各碰撞轴中心线的向量:
(3)

(4)
当条件d1>s、d2>s、d3>s均满足时,机器人手臂与障碍物之间距离均大于安全距离,不会发生碰撞。
当存在di≤s的情况时,则需要判断p到Li线段两端点是否满足状态二的两个条件才能判断机器人手臂与障碍物是否发生碰撞:
1)判断条件1的方法(以轴L2为例):L2两端点为L2b和L2c,∠pbc和∠pcb是p与线段的两个夹角,由余弦定理可得:
(5)
当且仅当夹角∠pbc和∠pcb二者为一个钝角、一个锐角的情况时,p点向L2的投影为情况b;
2)条件2的判断:通过两点间的距离计算公式可求得p到端点L2b和L2c的距离,并将其中的较小者min(L2b,L2c)与s比较,当min(L2b,L2c)>s时,该段路径的手臂轴与障碍物不会发生碰撞。
当以上情况均不满足时则会发生机器人手臂与障碍物的碰撞。
1.2.2 RRT*算法先验引导
标准RRT*算法在随机采样点的生成过程中有一个简单的生成引导机制:设置一个简单概率(一般情况为50%),生成随机采样点时基于这个概率以目标点作为生成的采样点,即每次生成采样点时有50%概率以目标点为生成点,进而对随机树的生长起到一定的引导作用,目的是为了避免因随机采样点的生成过于分散,产生过多的不必要树枝节点,进而影响算法轨迹结果的质量以及算法整体的运算速度,不过这种引导机制过于简单,虽然可以起到一定的引导作用,但是对轨迹结果的质量提高效果还达不到应用要求。以这种引导思想为基础,本文提出了优化的引导机制:先验引导机制。
先验引导算法思想:1)当随机树树枝生长至障碍物附近时,先计算能绕过障碍物、趋向目标点的最短方向,再控制生成随机采样点的三坐标方向向量大小,让其生成更倾向于计算出的方向;2)同1),在随机树树枝生长扩展时控制其生长方向三坐标方向向量大小以趋向计算出的方向;3)为了更快速找到终点,每成功生成一个新树枝节点都进行一次新树枝节点与目标点之间的轨迹障碍物碰撞判断,若两节点间的直线轨迹满足无碰撞需求,则下一次生长直接连接目标点以找到优化的避障轨迹。
具体算法原理如图5所示,以图5(a)圆柱体包围盒情况为例:1)当路径无障碍物碰撞时随机树正常生长树枝;2)当发生碰撞时,以碰撞位置前树节点与目标点的连线向量为方向向量对该树节点进行投影,将该树节点投影至过目标点且与X-Y平面垂直的平面上(此处该平面与X-Y平面垂直的处理是为了简化投影算法的计算,将3维空间中的投影简化为2维投影,如图5(a)主视图所示),投影后可以计算目前树节点距离障碍物边缘的最小z轴距离与最小y轴距离(此处为具体例子,实际应用中需要绕开的方向也可能是x轴与y轴的方向,或者其他可能的方向,原理相同不再枚举),对比可知此时树枝往y轴负方向生长最容易绕开障碍物、靠近目标点,故此时控制随机点向y轴方向以-1.5倍长度生成,向z轴方向以0.5倍长度生成,树枝生长方向也做相同处理,重复此过程至绕开障碍物,后重复1)、2)两步过程;3)在每次生长成功新的树枝节点后,判断生成的新树枝节点Xnew与目标点Xgoal之间的直连轨迹是否满足无碰撞需求,满足则下一次树枝生长直接以Xgoal为节点并完成生长,进而得到优化完成的避障轨迹。

图5 先验引导原理
包围球障碍物的处理原理与之相同。
2 试验结果与分析
为检验先验引导RRT*算法的性能,本文在MATLAB2021a上进行了仿真试验。试验软件环境为:Windows11,硬件配置:12th Gen Intel(R)Core(TM)i7-12700H2.30 GHz,内存(RAM)16 GB。三维仿真地图尺寸为:6 000×6 000×4 000(mm3),障碍物设置为球体(工装夹具)及圆柱体(机器人回转死区),具体障碍物信息如表2所示。包括8个球体障碍物和一个圆柱体障碍物。为了验证算法的鲁棒性,本文进行了两组试验,试验参数详见表3。表中需要说明的是:因为本文的目标点为工装夹具的装夹位置,第一组试验的目标点为工装夹具8的装夹位置,即为障碍球8所在位置,所以在第一组试验时表2中的障碍球8需要去除,否则会导致算法轨迹无法找到目标点。同理,在第2组试验中,目标点为工装夹具7的装夹位置,此时表2中的障碍球7需要去除。设置初始固定步长step为400 mm。
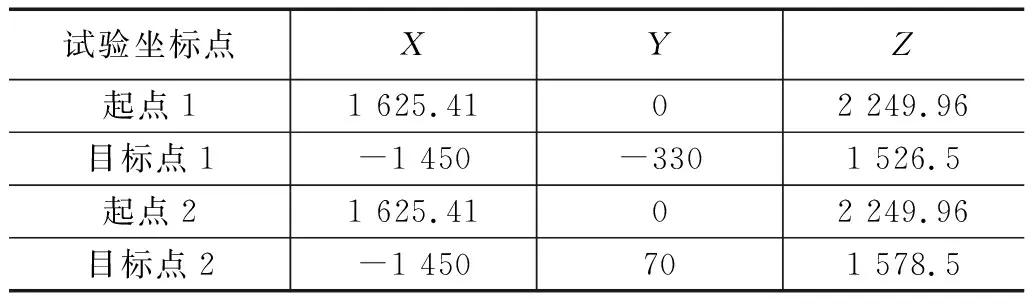
表3 起点与目标点信息表 mm
因为本文是以标准RRT*算法为基础进行的优化设计算法,故同时对标准RRT*算法与先验引导RRT*算法进行了对比仿真试验,试验1的结果如图6和图7所示,图6是两种算法得到的末端避障轨迹结果对比,其中图6(a)、(b)是标准RRT*算法的轨迹结果,图6(c)、(d)是先验引导RRT*算法的轨迹结果,由图可看出,先验引导RRT*算法所得末端轨迹更优于标准RRT*算法,其中由图6(b)、(d)主视图可看出,标准RRT*算法轨迹在中期为了能够绕过障碍物有明显的先下降后上升趋势,导致轨迹冗余,不满足轨迹优化需求。分析其原因是以固定步长绕过障碍物时,每一步都会前移较多距离,会导致轨迹在向y轴方向绕过障碍物时,向z轴方向进行较大的冗余位移,进而不断向下倾斜,当绕过障碍物后才能再往上趋向目标点。加入先验引导机制后轨迹下降/上升趋势消除,正是因为算法针对此现象有目的性地放大了y轴方向(目标位移方向)的扩展距离,同时减小了z轴方向(冗余位移方向)的扩展距离,进而轨迹得到优化。
图7是两种算法机器人运行末端避障轨迹的结果图,图中机器人均按实际现场运行要求姿态运行。图7(a)~(c)是标准RRT*算法结果,图7(d)~(f)是先验引导RRT*算法结果,由图可看出,两者均满足六轴机器人手臂与末端轨迹避障要求,机器人运行正常,包围盒算法有效。
试验1的最终末端轨迹长度分别为:先验引导RRT*算法3 483.13 mm,标准RRT*算法4 037.82 mm,轨迹优化14%左右。
试验2结果如图8和图9所示:图8是两种算法得到的末端避障轨迹结果对比,其中图8(a)、(b)是标准RRT*算法的轨迹结果,图8(c)、(d)是先验引导RRT*算法的轨迹结果,由图可看出,此时标准RRT*算法无法找到末端避障轨迹,随机树会卡死在机器人回转死区前,分析原因是碰撞节点与目标点连线方向在障碍物的中心面附近,生成的随机点不容易出现在绕过障碍物的部位,导致算法达到迭代次数上限,轨迹搜索失败停止。相反先验引导RRT*算法能够通过更大的y轴偏移量绕过障碍物,找到符合要求的末端避障轨迹。
图9(a)~(c)是先验引导RRT*算法机器人运行末端避障轨迹图,因标准RRT*算法未能找到完整末端轨迹,故此处没有标准RRT*算法的机器人运行图。由图可看出,机器人仍能够顺利运行所得的末端避障轨迹,所得结果有效。
综合对比试验1与试验2的结果可知,本文提出的先验引导RRT*算法在标准RRT*算法的基础上通过引入包围盒算法思想和先验引导思想,使算法能够生成满足机器人手臂与末端同时避障的轨迹;且相较于标准RRT*算法有更强的轨迹搜索能力,能够绕开条件更苛刻的障碍物;有更强的轨迹优化能力,最终轨迹缩短14%左右。
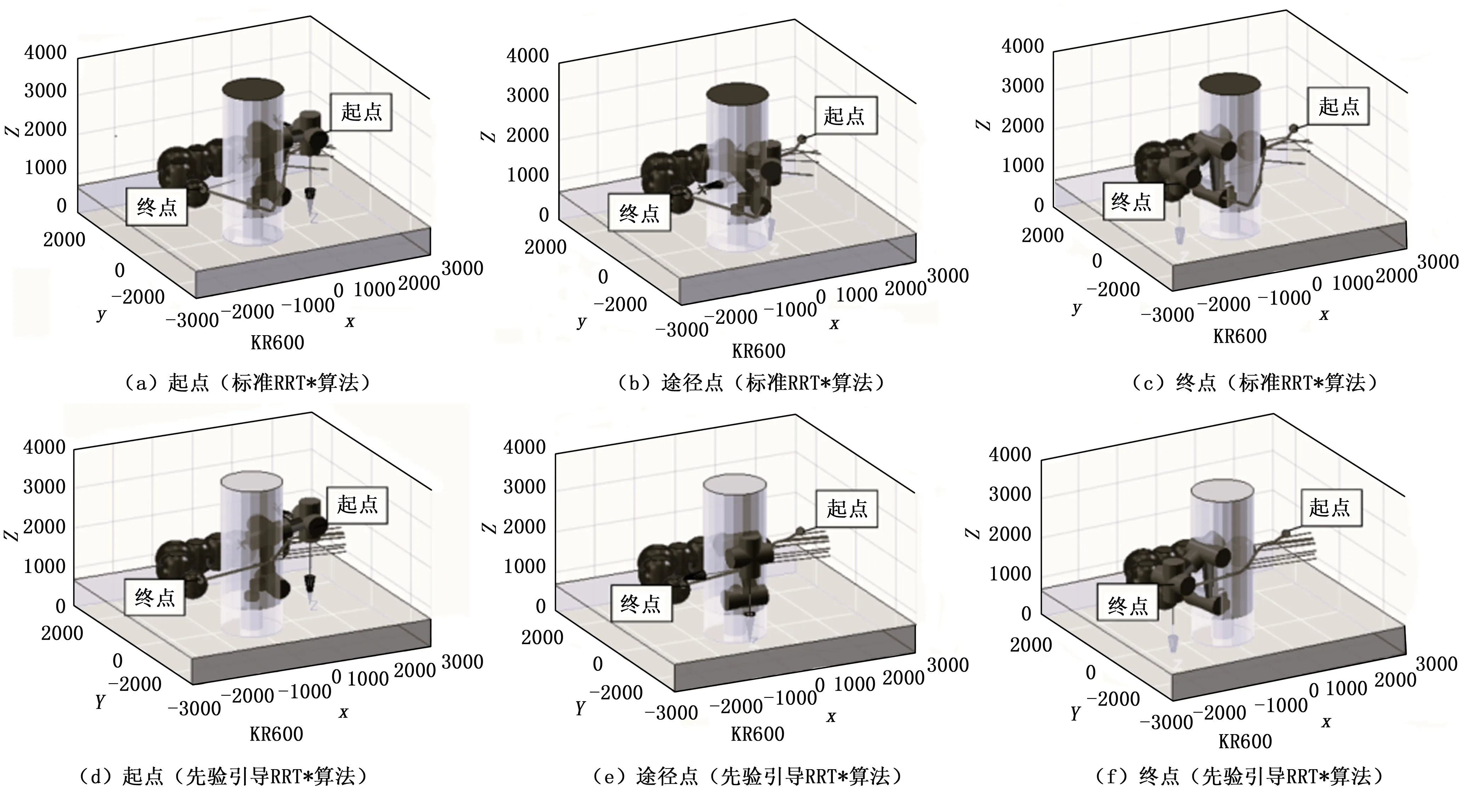
图7 目标点1机器人避障轨迹运行结果

图8 目标点2仿真试验末端避障轨迹结果

图9 目标点2机器人避障轨迹运行结果
3 结束语
本文针对六轴工业机器人实际装配中的避障需求,以标准RRT*算法为基础进行优化算法设计,提出了先验引导RRT*算法:1)针对标准RRT*算法只生成末端避障轨迹,不能满足机器人手臂避障需求的问题,本文融入包围盒算法,加入机器人手臂碰撞检测,进而使生成的轨迹同时满足机器人末端与手臂均不发生碰撞的需求;2)针对标准RRT*算法的轨迹优化能力、轨迹搜索能力不能满足现场装配需求的问题,参考其随机点生成引导机制,提出了先验引导机制。通过先计算最优绕开障碍物、趋向目标点的方向,后对随机点生成方向与随机树生长方向进行计算方向引导的机制以优化标准RRT*算法的轨迹优化能力、轨迹搜索能力来满足现场装配的要求。
相较于标准RRT*算法,本文提出的先验引导RRT*算法有更强的轨迹搜索能力与轨迹优化能力,且所得轨迹满足机器人末端与手臂同时避障的需求。能够绕开标准RRT*算法无法绕开的苛刻条件障碍物,能缩短算法轨迹14%左右,达到了现场装配的避障轨迹需求。
