点线面位置关系探究中的多种思维方法

■王小丽

高考对立体几何的考查始终围绕“空间问题平面化、模型化和代数化”展开,借助热点问题探究求解中的“多种思维方法”,可以提高“构建函数模型、直观想象、逻辑推理、合理运算”等核心素养。

热点1：正方体“截面最值”求解中的多种思维方法

例1已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则平面α截此正方体所得截面面积的最大值为____。

解法1：直接作截面构建目标函数求最值。如图1,平面A1C1B与每条棱所成的角相等,这时符合题意。现把平面A1C1B平移,得到如图2所示的六边形EFGHMN,下面求截面EFGHMN的面积的最大值。

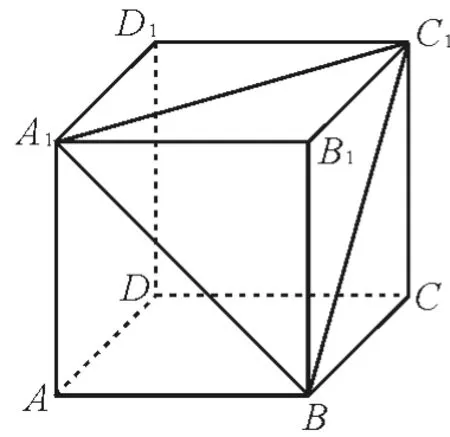
图1

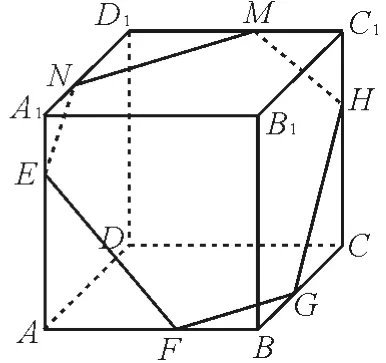
图2

设A1N=x,则EN=,MN=。根据对称性可知EF=(1-x),FG=x。

如图3,延长EN,HM相交于点P,延长EF,HG相交于点Q。

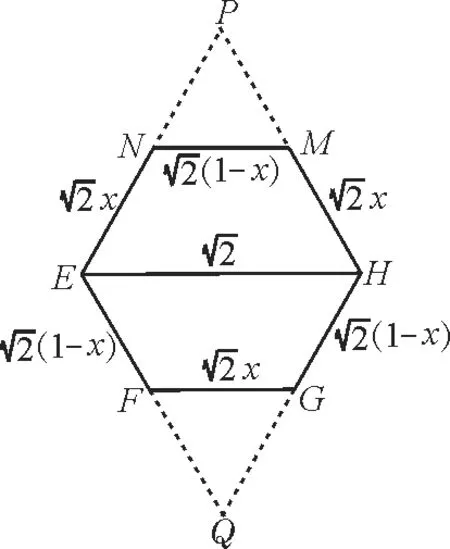
图3

由相似比可得PN=PM=(1-x),QF=QG=。

易得∠HEF=∠EHG=60°,可知△EHQ和△EHP为 等 边 三 角 形,所 以S六边形EFGHMN=S△EHP+S△EHQ-S△PMN-S△FGQ。

解法2：由特殊位置确定其最大值,如图4。

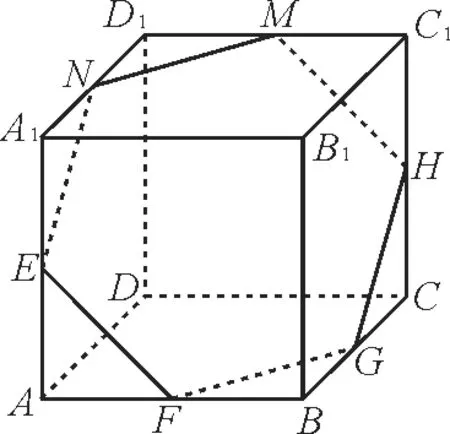
图4

由题设可知,截面α应与正方体的体对角线垂直,当平面α平移至截面为正六边形时,其面积最大,这时正六边形的边长为。易得最大面积为

友情提醒：求正方体的截面最值的方法常用特殊位置法,这种方法解题简捷明快,但需要有一定的解题经验,特别是解答选择题,这种方法值得同学们重视。

热点2：异面直线所成角求解中的多种思维方法

例2如图5,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1= 3,则异面直线AD1与DB1所成角的余弦值为_____。

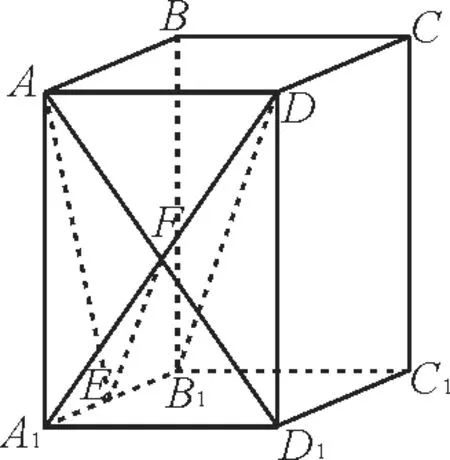
图5

解法1：平移法求异面直线所成的角。在长方体ABCD-A1B1C1D1中,取E为B1A1的中点,F为AD1与A1D的交点。由几何关系可知,DB1//FE,所以∠EFA=θ为

解法2：补形法求异面直线所成的角。在长方体ABCD-A1B1C1D1的右侧补一个完全相同的长方体DD1C1C-FGHE,如图6。

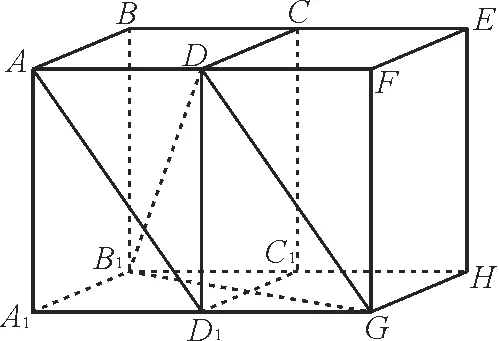
图6

友情提醒：几何法求异面直线所成的角,通过“直接平移或补形平移”得到两条异面直线的夹角或其补角,切记异面直线所成角的取值范围为(0°,90°]。

热点3：直线与平面所成角求解中的“几何法和间接法”

例3如图7,四边形ABCD为正方形,E,F分别是AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF。

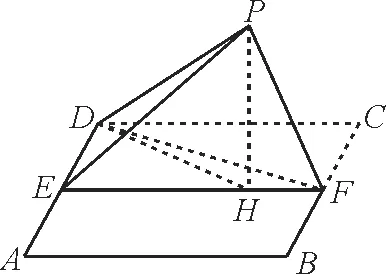
图7

(1)证明:平面PEF⊥平面ABFD。

(2)求DP与平面ABFD所成角的正弦值。

解：(1)由折叠前后不变的线线垂直关系得BF⊥PF,BF⊥EF。因为PF∩EF=F,所 以BF⊥平 面PEF。又BF⊂平 面ABFD,所以平面PEF⊥平面ABFD。

(2)(方法1)利用几何法求线面角。作PH⊥EF,垂足为H。由(1)知平面PEF⊥

友情提醒：解答这类问题,关键是把握折叠前后线段长度,以及线线垂直关系的变化。无论是几何法求线面角,还是等积法求线面角,其解题的根本是在三角形中进行的。