基于改进粒子群的绳驱连续型机械臂逆运动学分析*

余 鑫，武海雷，丁 萌，郑先杰

(1.南京理工大学 自动化学院·南京·210094；2.上海航天控制技术研究所·上海·201109)

0 引 言

随着人类对太空的不断探索，空间机械臂已被应用到多种在轨任务中，如飞行器对接、航天器故障维修等[1]。然而，传统刚性机械臂自由度受限，工作空间相对固定，难以适用于狭小的非结构化空间。连续型机械臂因其自身的弹性结构，具有良好的弯曲性能，能够灵活地改变自身的形状。因此，利用连续型机械臂代替传统刚性机械臂，可以更好地满足狭窄空间作业任务需求。

连续型机械臂设计灵感来源于对象鼻、章鱼臂等生物的仿生研究。现有的连续型机械臂按照驱动方式的不同，主要分为：气动和液压驱动连续型机械臂[2-3]、同心管连续型机械臂[4]、记忆合金机械臂[5]以及绳驱连续型机械臂[6]。连续型机械臂与具有刚性连杆和传统关节形式的刚性机械臂不同，其通过柔性构件的弹性变形产生连续弯曲运动，运动学建模更为复杂。Geng S.N.等[7]利用分段常曲率假设，建立三关节连续型机械臂的运动学模型，得到驱动空间、关节空间以及操作空间的映射关系，但该模型没有考虑多关节之间的耦合。R.Roy等[8]利用伪刚体的思想，将连续型机械臂简化为多个相连的刚性连杆，相邻的连杆之间具有弯曲和旋转两个自由度，利用修正后的D-H参数得到运动学模型，但这种模型只适用于弯曲幅度较小的运动，并且所采用的关节参数不能直观反映机械臂的连续变化。F.Renda等[9-10]分析了连续型机械臂的结构特点，利用Cosserat杆理论，将连续型机械臂离散成有限的节段和自由度，建立其运动学模型。

由于连续型机械臂的正运动学模型表达式过于复杂，难以得到逆运动学模型的解析解。B.A.Jones等[11]分析了操作空间到关节空间的映射关系，得到了单关节连续型机械臂的逆运动学关系，但该方法难以推广到多关节机械臂。刘闯等[12]利用分段常曲率假设建立正运动学模型，得到连续型机械臂的雅可比矩阵，通过牛顿迭代法得到逆运动学数值解。K.Dmitrii等[13]采用FABRIK算法解决逆运动学问题，通过迭代的方式逐步搜索关节角，直到机械臂末端完全到达目标点。然而，基于迭代的逆运动学求解方法通常计算量大，且迭代精度和收敛速度均受到迭代初值的影响，给连续型机械臂的实时操作带来困难。A.Amouri等[14-15]将连续型机械臂的逆运动学问题转化为优化问题，利用元启发式算法，解决了具有超冗余性与复杂耦合性的机械臂逆运动学求解问题，获得了具有更高精度的逆运动学解，但是该逆运动学模型只建立了机械臂末端位置和绳长的关系，不能反映机械臂的形态变化。

本文针对一类两节绳驱连续型机械臂，基于分段常曲率假设建立了正运动学模型，并分析了多节之间的运动耦合关系。利用改进的粒子群优化(Particle Swarm Optimization，PSO)算法求解得到连续型机械臂的逆运动学模型。搭建了绳驱连续型机械臂的物理样机，对所建运动学模型进行了实验验证。

1 绳驱连续型机械臂结构

两节绳驱连续型机械臂示意图如图1所示，该连续型机械臂由中心弹性杆、间隔盘以及驱动绳组成，机械臂由2节组成，每节包含5个间隔盘以及3根驱动绳。间隔盘固定在弹性杆上并等距分布，作为刚性支撑，间隔盘的结构如图2所示，其中图2(a)为第1节机械臂的间隔盘结构，6个驱动绳引导孔均匀分布在中心孔周围，图2(b)为第2节机械臂的间隔盘结构，3个驱动绳引导孔均匀分布。驱动绳穿过中间间隔盘，固连在相应关节最后一个间隔盘上，利用电机对驱动绳进行收放可以使机械臂发生弯曲形变。

图1 绳驱连续型机械臂示意图Fig.1 Sketch of the cable-driven continuous manipulator

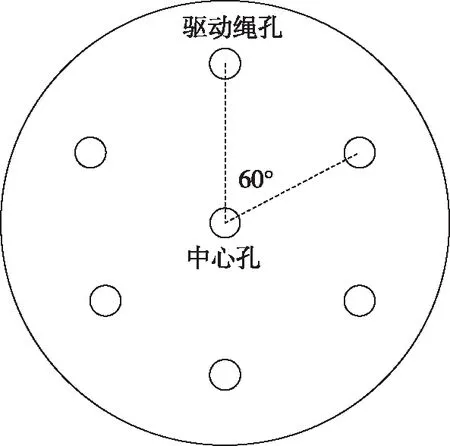
(a)第1节间隔盘

2 正运动学

第i节机械臂弯曲示意图如图3所示，为了建立绳驱连续型机械臂的正运动学模型，在基座间隔盘上建立坐标系Oi-1Xi-1Yi-1Zi-1，其中，坐标系原点Oi-1位于间隔盘中心点，Xi-1轴方向为中心点到第一根驱动绳的方向，Zi-1轴方向为沿着中心杆垂直于间隔盘向上，Yi-1轴方向由右手定则确定。然后，以坐标系Oi-1Xi-1Yi-1Zi-1为基坐标系，在末端间隔盘上建立坐标系OiXiYiZi，其初始方向与基坐标系一致。

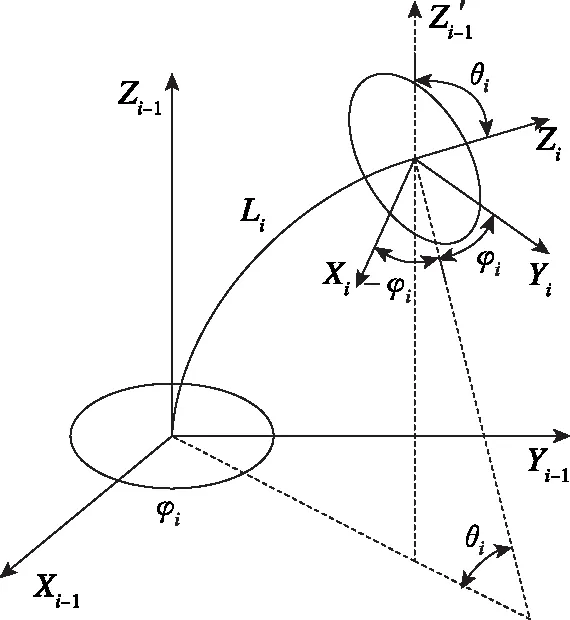
图3 连续型机械臂弯曲示意图Fig.3 Sketch of the continuous manipulator bending

绳驱连续型机械臂通过驱动绳的收放使得中心弹性杆发生弯曲，进而达到机械臂末端运动的目的。机械臂每节有2个自由度，包括由弹性杆形变产生的弯曲自由度和围绕Z轴旋转产生的旋转自由度，分别用θi和φi表示这2个自由度。

n节绳驱连续型机械臂的正运动学模型，即由关节空间的变量θi和φi求解操作空间中机械臂的末端位姿，可以表示为末端坐标系OnXnYnZn和基坐标系O0X0Y0Z0的映射关系0Tn，由上述分析可知

0Tn=0T11T2…n-1Tn

(1)

基于分段常曲率假设，在忽略外力、重力以及驱动绳和间隔盘之间的摩擦力后，连续型机械臂在运动时，每节可近似为一段等曲率的曲线，由此，式(1)中齐次变换矩阵i-1Ti可表示为

(2)

式中，Li表示第i节的长度，cφi=cos(φi)，sφi=sin(φi)，cθi=cos(θi)，sθi=sin(θi)。

3 基于PSO的逆运动学求解

绳驱连续型机械臂的逆向运动学，需要建立操作空间到关节空间以及关节空间到驱动空间的映射关系，也即在已知末端位姿时求取关节变量和绳长的变化量。为了避免复杂的雅可比矩阵的求解，本文将逆运动学问题转化为优化问题，并利用改进的粒子群算法对优化目标进行求解。

3.1 操作空间到关节空间的映射

由式(1)和式(2)可知，单节连续型机械臂的逆运动学求解较简单，但对于多节连续型机械臂，其正运动学表达式非常复杂，难以像传统的六自由度刚性机械臂一样求解出解析解。此外，由于冗余性的存在，对于同一个目标位置，可能会存在多组θi和φi与之对应，因此，如何选取合适的解也是必须要解决的问题。本文为了简单高效地完成逆运动学的求解工作，从优化的角度出发，利用粒子群算法完成操作空间到关节空间的映射求解。

3.1.1 优化目标

由于逆运动学求解存在多解的情况，在实际的机械臂运动中，通常需要选择一组最优解作为目标解，使得机械臂在运动过程中满足能量消耗和安全性等方面的约束。本文在进行逆运动学求解时，从能量最优的角度确定优化目标。

设机械臂的目标位置为[xd，yd，zd]，其中xd，yd，zd为位置坐标，当前位置为[xc(q)，yc(q)，zc(q)]，其中，q代表机械臂的4个关节变量，即q=[θ1，φ1，θ2，φ2]，那么机械臂末端的实际位置和期望位置的误差Δ为

Δ=

(3)

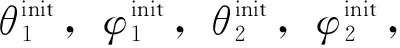
(4)

由此，本文的优化目标为在满足末端位置误差Δ小于允许的最大误差Δmax时，关节角度的变化最小，如式(5)所示

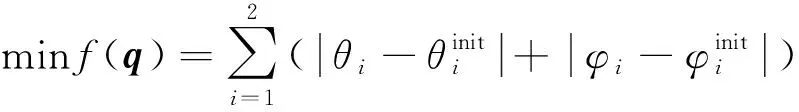
(5)

其中，g(q)表示约束函数，代表末端位置误差与最大允许误差之间的差值。为方便后续处理，利用罚函数法将式(5)所示的约束最优问题转化为无约束最优问题，如式(6)所示

(6)

其中，f′(q)表示转换后的目标函数；g′(q)为惩罚项；λ表示惩罚系数。

3.1.2 利用PSO求解

粒子群算法模拟了鸟群觅食的过程，鸟群中的每只鸟(粒子)通过对自身最优位置和群体最优位置的学习而不断更新自身的位置，从而达到全局最优解。粒子群算法的基本流程如图4所示。

图4 粒子群算法基本流程Fig.4 Basic flow of PSO

首先，设置基本粒子量x，针对绳驱连续型机械臂逆运动学的实际情况，将关节变量(θ1，φ1，θ2，φ2)作为基本粒子。其次，采用随机生成的方式初始化粒子种群X=(x1，x2，…，xn)以及每个粒子的初始速度V=(v1，v2，…，vn)，每次循环中，通过对适应度函数的计算，每个粒子可以得到自身历史最优位置和全部粒子的最优位置，从而利用式(3)和式(4)更新自身的速度和位置。

(7)

(8)

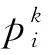
惯性权重ω(k)是粒子群速度更新的一个重要参数，它的大小决定着粒子的搜索能力。经典的粒子群算法中，利用线性递减函数作为惯性权重，这种方式使得在算法初期粒子速度变化较大，具有良好的全局搜索能力，在迭代后期粒子速度变化较小，局部搜索性能好。但是惯性权重采取这种线性递减的方式，使得在算法的迭代次数较大时，粒子几乎没有搜索能力，一旦粒子陷入局部最优就很难跳出来，本文中改进的惯性权重如式(9)所示

(9)

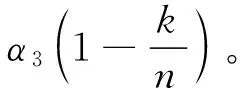
3.2 关节空间到驱动空间的映射

在利用粒子群算法得到操作空间到关节空间的映射后，利用几何分析法建立关节空间到操作空间的映射关系。如两关节连续型机械臂在运动过程中，两节之间存在运动耦合，在第1节单独运动时，会造成第2节驱动绳的绳长也发生变化，因此在求取关节空间到驱动空间的映射时需要进行解耦。假设第1关节的关节量为θ1，φ1，第2关节不发生运动，则第2关节的耦合量为

(10)

式中，Δl′2i(i=1，2，3)表示第1关节单独运动时对第2节3根驱动绳造成的耦合量；r2表示中心弹性到第2关节驱动绳之间的距离；n1为第1关节间隔盘数量；L1为第1节的长度。

由此，关节空间到驱动空间的映射关系如下

(11)

(12)

式中，Δl1i、Δl2i(i=1，2，3)分别表示两节3根驱动绳的变化量；r1为中心杆到第1节驱动绳之间的距离；n2为第2关节间隔盘数量；L2为第2节的长度。

3.3 仿真验证

为了验证改进的粒子群算法求解绳驱连续型机械臂逆运动学的有效性，将其与基于标准粒子群算法的求解结果进行对比仿真分析。仿真平台采用的CPU为i7-7700HQ，主频2.8GHz。设置种群大小为50，最大迭代次数为100，自身学习因子c1=1.3，全局学习因子c2=1.7，罚函数系数λ=1，最大允许误差Δmax=5。两节绳驱连续型机械臂的相关参数：L1=L2=300mm，n1=n2=5，r1=18mm，r2=16mm。随机选取5个末端位置，利用本文所述改进粒子群算法以及标准粒子群算法进行逆运动学的求解，所求得的关节变量值、计算耗时以及误差分别列于表1和表2中。

表1 基于改进粒子群算法的逆运动学求解结果

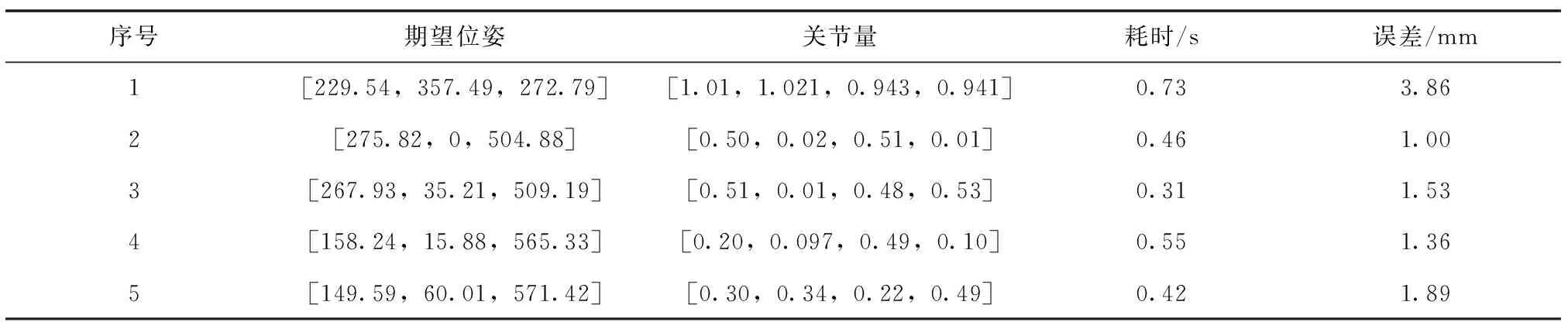
表2 基于标准粒子群算法的逆运动学求解结果

如表1和表2所示，对随机选取的末端位姿，利用改进的粒子群算法能够快速得到相应的逆运动学结果，并且求解误差在允许范围之内，满足实际使用的需求。

4 实验分析

为了验证本文基于分段常曲率假设建立的绳驱连续型机械臂的运动学模型，本文搭建了单节机械臂的物理样机系统，如图5所示。该系统由机械臂本体、驱动部分、视觉部分等组成，其中机械臂包含10个间隔盘以及1个基座盘，各盘之间间隔60mm，机械臂总长600mm，由3根绳子驱动，驱动绳引导孔到中心杆孔的距离是25mm。

图5 连续型机械臂物理样机系统Fig.5 Prototype of continuum manipulator system

利用上述物理样机系统进行单节机械臂的弯曲实验。实验中，机械在初始状态时，关节角θ=0°、φ=0°。在弯曲平面角φ保持不变的情况下，通过理论模型计算机械臂弯曲10°、20°、30°和40°时的绳长变化量，将这些变化量施加到实际物理样机系统中，可得到机械臂的弯曲情况如图6所示。

图6 单节机械臂弯曲实验示意图Fig.6 Schematic diagram of bending experiment

利用双目视觉系统可以测量各个弯曲阶段的末端位置，记录在表3中。表3还记录了机械臂弯曲相同度数时，理论模型下的末端位置。

表3中的误差计算方式为两种情况下的末端位置到初始末端位置之间距离的差值和机械臂总长的比值。从实验结果可以看出，理论模型与实验结果之间的误差较小，证明了基于常曲率的运动学模型可以在一定程度上描述绳驱连续型机械臂的运动特征。另一方面，随着机械臂弯曲角度的变大，误差逐渐增加，考虑到机械臂本身质量较小，受重力的影响较小，因此，误差的主要来源是理论模型所依赖的常曲率假设。

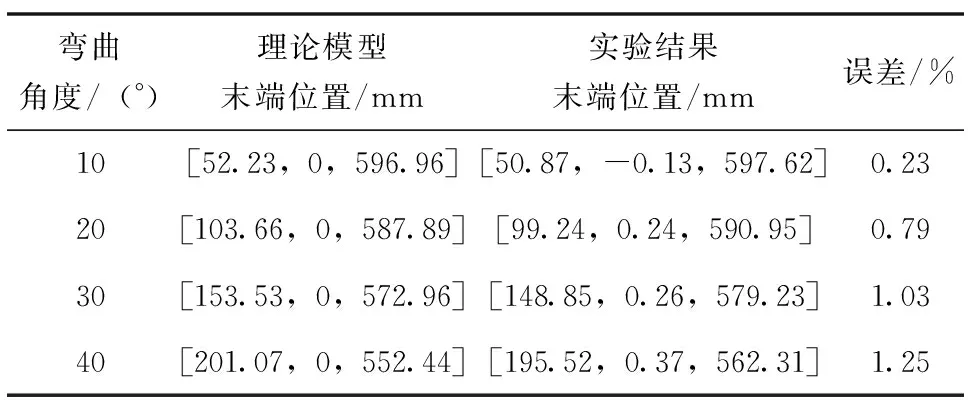
表3 单节机械臂弯曲结果

5 结 论

本文针对一种多节绳驱连续型机械臂，基于常曲率假设建立了机械臂的正运动学模型，并对机械臂关节之间的运动学耦合关系进行了分析，在此基础上提出了利用改进PSO算法对连续型机械臂的逆运动学进行求解。仿真结果表明，该方法能快速求解逆运动学，且误差相对较小。最后，搭建了绳驱连续型机械臂的物理样机系统，对本文所建正运动学模型进行验证，分析了分段常曲率假设的误差大小。本文所提方法可推广应用于多节绳驱连续型机械臂的逆运动学求解，但是对于多节连续型机械臂的逆运动学多解问题，还需进一步开展研究。