一题一课，让教学走向深入

方菲

［摘 要］以人教版数学教材六年级上册中的“绳捆圆柱的周长问题”为例，通过课前思考、教学设计和教学反思开展教学活动，带领学生研究用胶带捆扎2罐、3罐、4罐薯片的方法，让学生发现计算胶带总长的方法以及将薯片罐捆成正方形更节约胶带的规律，从而对“绳捆圆柱的周长问题”有更加全面的理解。

［关键词］一题一课；周长；绳捆圆柱

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）05-0051-03

一题一课，就是教师在一节课上带领学生围绕一道数学题或者一类数学题展开深入的交流讨论，实现“做一题通一类”的教学效果。一题一课不仅能让学生理解数学本质，还能让教学走向深入。

一、课前思考

为方便销售，售货员将啤酒瓶捆成如图1所示的形状（从瓶底方向看），如果每组分别捆5圈绳子（接头处不计），每组至少需要多长的绳子？你发现了什么？

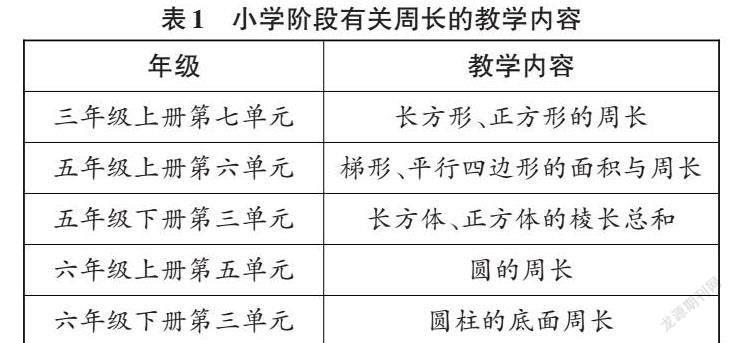
这是人教版数学教材六年级上册第66页中的一道练习题，学生在解决这道练习题的过程中，需要发现绳子的长度是由一个圆的周长和若干条直径组成的，最外圈有多少个圆柱形物体，就有多少条直径。在一题一课的课堂上，教师不应只教学这道练习题，还要从学生的认知起点出发，帮助学生将此问题转变成若干个已经学过的数学知识点，为后期要学习的知识做好铺垫。为此，笔者梳理了小学阶段有关周长的教学内容（见表1）。

笔者发现，学生在三年级接触的平面图形的周长以及在五年级接触的立体图形的棱长总和，涉及的线都是直的，而在六年级接触的圆的周长和圆柱的底面周长，涉及的线是弯曲的。同时，笔者以这道练习题对六年级其中两个班级共90名学生进行前测：捆2瓶啤酒需要的绳子长度为（3.14×7+2×7）×5=179.9（厘米），学生解答正确率是64.4%；捆3瓶啤酒需要的绳子长度为（3.14×7+3×7）×5=214.9（厘米），学生解答正确率是50%；捆4瓶啤酒需要的绳子长度为（3.14×7+4×7）×5=249.9（厘米），学生解答正确率是32.2%。

随着啤酒瓶数量的增加，学生计算的正确率为什么会降低？笔者尝试围绕这道练习题设计了一节“绳捆圆柱的周长问题”的课，以帮助学生更好地用数学知识解决生活中的问题。

二、教学设计

1.确定教学目标

学生要正确解决这道题，需要具备语文阅读理解能力和将文字转变成图、圆的周长公式等能力，如此才能发现捆扎的规律。对此，笔者确立了“绳捆圆柱的周长问题”一课的教学目标：（1）经历提出问题和分析、解决问题的过程；（2）沟通数学规律和生活原型，探索解决问题的方法和策略；（3）在解决问题的过程中感受数学与生活的联系，提高学生的数学学习兴趣。

2.确定教学过程

（1）分析并解决问题

题目：超市在开展促销活动，薯片“买一送一”。售货员用胶带将2罐薯片紧紧地捆在一起，薯片罐的底面直径是7厘米，只捆1圈（接头处不计），需要用多长的胶带？

师：你能想象出将2罐薯片捆扎在一起，从底面看是什么形状吗？在纸上画一画。

生1：从底面看是两个紧紧贴在一起的圆形。

师：那捆绑的胶带是什么形状？胶带的长度是多少呢？

生2：捆绑的胶带的图形可以看成是2个半圆和1个正方形的组合图形。

生3：胶带的长度是3.14×7+4×7=49.98（厘米），我的理解是2个半圆拼起来是一个圆，这个圆的周长是3.14×7，再加4条直径的长度。

生4：我不同意这个答案，胶带的长度应该是3.14×7+2×7=35.98（厘米），即1个圆的周长加其2条直径的长度。

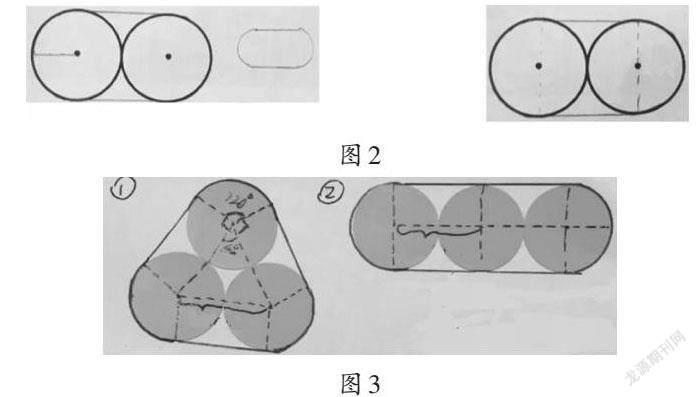
师：我们先来看看同学们画的这两幅图（如图2），你觉得哪一幅可以清楚地表达解题过程？

生5：我觉得第二幅图好，因为它清楚地画出了2个半圆和1个正方形。

【设计意图】“绳捆圆柱的周长问题”一课让学生经历了将生活原型转化为数学问题的过程。为了解决捆扎2个圆柱所用的胶带总长的问题，学生在画图中发现胶带总长分为直线和曲线两部分，直线部分是2条直径，曲线部分是1个圆的周长，从而计算出胶带总长。

（2）激活经验，探索解题策略

【案例1：捆扎3罐薯片的方法】

师：如果捆扎3罐薯片，可以怎么捆？

学生的两种方法（如图3）：第一種是分成了上下两层，从底面看像一个三角形，所用胶带的长度等于1个圆的周长加上3条直径，为3.14×7+3×7=42.98（厘米）；第二种是排成一排捆扎，从底面看是2个半圆和1个长方形，所用胶带的长度等于1个圆的周长加上4条直径，为3.14×7+4×7=49.98（厘米）。

【案例2：捆扎4罐薯片的方法】

师：如果捆扎4罐薯片，可以怎么捆？

学生的两种方法（如图4）：第一种是排成一排捆扎，从底面看是2个半圆和1个长方形，所用胶带的长度等于1个圆的周长加上6条直径，为3.14×7+6×7=63.98（厘米）；第二种是分成上下两层，所用胶带的长度等于1个圆的周长加上4条直径，为3.14×7+4×7=49.98（厘米）。

【在比较中发现捆扎的规律】

师：观察捆扎2罐、3罐、4罐薯片所用胶带的长度（见表2），你有什么发现？

生1：胶带的总长都分成直线和曲线两部分，曲线部分都是1个圆的周长。叠起来捆所用的胶带比排成一排捆所用的胶带少，而且每增加1罐，叠起来捆的胶带总长就会增加1条直径的长度。

师：你能利用这些规律快速算出捆6罐排成一排的薯片所用的胶带总长吗？

生2：排成一排的话，每增加1罐，胶带总长增加2条直径的长度，捆6罐所用的胶带总长是3.14×7+10×7=91.98（厘米）。

通过比较，学生得出了这样两个捆扎结论：一是计算上不管几罐捆在一起，所用胶带的长度都是1个圆的周长加上若干条直径；二是在捆扎方法上，多排捆扎比单排捆扎更节约胶带。

【探讨多排比单排捆扎更节约胶带的原因】

师：为什么多排比单排捆扎更节约胶带？其实这个问题我们在三年级的时候就学过了，当时我们是研究拼16个小正方形，哪一种拼法周长最短。

生1：周长最短的图形是正方形，因为16个小正方形的周长是固定的，拼成4×4的时候中间的公共边是最多的，所以外面的周长自然就短了。

师：面积相等的图形，长和宽越接近，周长越短，在这道题中，我们可以把圆看成正方形来理解。

【设计意图】在这个环节中，笔者带领学生经历四个学习过程：研究捆扎3罐薯片的方法；研究捆扎4罐薯片的方法；在比较中发现捆扎的规律；探讨多排比单排捆扎节约胶带的原因。学生在独立思考、小组学习、全班交流中体会捆扎方法的多样性，发现捆扎方法中的规律。另外，为了解释多排比单排捆扎更节约胶带的原因，笔者通过沟通前后知识，让学生体会数学思想方法的相关性。

（3）联系生活，逆向解决问题

师：现在，你们明白生活中为什么将蔬菜、小棒、钢管等捆扎成正方形了吗？

师（出示题目）：“啤酒节”活动促销卖啤酒，啤酒瓶的直径是5厘米，胶带只绕一圈（接头处不计），若售货员只有45.7厘米长的胶带，请你从图5中帮她选择合适的捆法。

生1：我是这样想的，胶带长度是 45.7 厘米，我就把每一种捆法的胶带长度都算出来。第一种捆法的胶带长度是3.14×5+7×5=50.7（厘米）；第二种捆法的胶带长度是3.14×5+8×5=55.7（厘米）；第三种捆法的胶带长度是3.14×5+6×5=45.7（厘米）；第四种捆法的胶带长度是3.14×5+8×5=55.7（厘米）。因此，应该选第三种捆法。

生2：根据刚才的捆扎规律，每种捆法都有1个圆，我先把圆的周长减掉，45.7-3.14×5=30（厘米），圆的直径是5厘米，30÷5=6（条），胶带只够捆绑6条直径的长度，而第三种捆法有6条直径，正好符合。

【设计意图】为了让学生对“绳捆圆柱的周长问题”有全面深刻的理解，笔者出示的题目中告诉学生胶带的总长，让学生利用已经发现的捆扎规律选择符合要求的捆法，这是要求学生运用逆向思维解决数学问题，进一步帮助学生巩固捆扎的规律和计算方法。

三、教学反思

这节数学课中似乎只讲了一道数学题，但是笔者通过这一道题引出相关的一类题，在层层推进中使学生对“绳捆圆柱的周长问题”有更加深刻的理解，这就是一题一课教学活动的优势，不仅挖深了主体知识，还串联了相关知识。

1.坚持学生立场，引发真实学习

数学课堂是学生探究数学知识和发现数学奥秘的主阵地。因此，教师在教学过程中要尊重学生的认知特点，设计适合他们探究的学习内容。为了精准把握学情，笔者通过课本中的一道“绳捆圆柱的周长问题”进行前测，了解了学生在解决这个问题时遇到的困难，使教学有更加充分的预设和铺垫。在学习方式上，笔者放手让学生自主探究，先暴露他们的知识盲区，再利用课堂时间进行纠错，最后促进学生对数学知识的理解。

2.整体建构知识，拓宽思维深度

一题一课聚焦一类题，形成一节课，可拓宽学生数学思维的深度、广度和灵活度。在这一课中，笔者先以生活原型引出数学问题，再让学生经历从简单问题到复杂问题的解决过程，然后发现不同捆法的计算方法和规律，试着利用捆扎的规律逆向解决问题，整体建构了“绳捆圆柱的周长问题”的知识框架，有利于学生在学习中形成结构性思维。

3.联系生活实际，解决生活问题

数学源于生活，又回歸于生活。在课堂开始，笔者通过让学生欣赏生活中的钢管、白菜、啤酒瓶捆法等引出捆扎薯片的生活情境，再从捆扎薯片罐的底面抽象出圆形。在课堂最后，笔者引导学生通过计算周长推测啤酒瓶的捆扎方式。整节数学课在探究中不断将生活问题转化为数学问题，从而利用数学知识解决实际问题。

综上，一题一课以一道数学题或一类数学题为学生开启数学学习的新天地。在数学课堂上，教师应深入地挖掘或变换学习素材，在一类数学学习中实现思维走向深刻，在求联中沟通知识之间的关系，在拓展中促使学生走向高阶思维。

［ 参 考 文 献 ］

[1] 明启文.引导学生在典型圆周长的测量中发现圆周长与直径的关系：“圆的周长”教学赏析[J].云南教育（小学教师），2020（12）：41-42.

[2] 史勤蒙.教学现场的透视与教学细节的分析：以“圆周长的计算”教学为例[J].小学教学研究，2019（13）：65-67.

[3] 郑群.抓住数学本质，设计有深度联系的数学任务：以“圆周长的拓展练习”为例[J].小学教学设计，2020（Z4）：70-72.

（责编 覃小慧）