风雷软件LES 开发设计与验证

张子佩，赵钟，，陈坚强，刘健，邓小兵

1．空气动力学国家重点实验室，绵阳 621000

2．中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

进入21 世纪以来，计算流体力学（Computational Fluid Dynamic， CFD）的快速发展和广泛应用极大地改变了航空航天飞行器设计过程，不仅能有效减少物理试验次数，还可模拟一些物理试验无法开展的工况，已成为飞行器设计过程中必不可少的方法手段。

当前，计算流体力学的研究方法正从以定常、小范围分离或附着流动为特征的RANS（Reynold-Averaged Numerical Simulation）湍流模拟，向非定常、大范围分离和流动掺混为特征的非线性多尺度问题转移。RANS 方法能够很好地预测定常小范围分离或附着流动，但对大范围分离流动的模拟能力不足。大涡模拟（Large Eddy Simulation， LES）[1］和直接数值模拟（Direct Numerical Simulation， DNS）[2］方法被认为是解决这类问题的有效手段。DNS 方法对流动中的所有尺度进行直接求解，模拟高雷诺数流动需要的网格量达到了Re37/14L量级[3］。LES 方法只对流动中的大尺度脉动直接求解，对小尺度脉动采用模化方法，分为壁面解析的大涡模拟（Wall-Resolved LES， WRLES）和壁面模化的大涡模拟（Wall-Modelled， WMLES）。对于低雷诺数流动，两者所需的网格量差异不大，但对于高雷诺数流动，前者需要的网格量为Re13/7L，后者需要的网格量为ReL[3］。按当前计算机的发展水平，即使对106量级雷诺数下的小展弦比机翼模拟，预计也要到2030年，WMLES 才可以在24 h 内完成[4］。

LES 的基本思想是选择处于惯性子区内的滤波尺度，将湍流脉动量分为可以数值求解的大尺度脉动量和需要亚格子尺度（Subgrid Scale，SGS）模型模化的小尺度脉动量，由于小于滤波尺度的脉动量接近于各向同性，所以亚格子模型比RANS 模型更为容易和普适。对于大尺度脉动量所主导的流动问题，例如气动噪声[5］、湍流燃烧[6］、激波/边界层干扰[7］、大范围分离流动[8］等领域，LES 方法正在发挥着越来越重要的作用。

为了推动LES 方法尽快走向成熟应用，学者正从多个方面开展研究，主要包括：空间离散格式、时间推进格式、亚格子模型、入流生成方法、壁面模化方法、非结构网格应用、软件工程化等。

空间离散格式方面，迎风格式的适用性是焦点。一般认为RANS 方法常用的二阶迎风格式耗散性大，会使亚格子模型的截断波数难以确定，尤其是对复杂构型而言，由于非均匀湍流的存在，截断波数更加难以确定，因而对高阶迎风格式提出更迫切的需求[9］。

时间推进格式方面，较低的时间精度会使高精度的空间离散方法无法达到效果，Choi 和Moin[10］认为时间步长需满足u2τΔt/ν ＜1，其中uτ为壁面摩擦速度，Δt 为时间步长，ν 为黏性系数。

亚格子模型方面，Nicoud 等[11］认为涡黏性模型需要满足4 个特性：①只利用流场的当地量，并且要保正；②满足近壁渐进特性；③在刚性转动、纯剪切或者二维流动中，模型退化为0；④在单纯轴对称或者单纯各向同性膨胀/收缩流动中，模型退化为0。

壁面模化方法方面，对于Re＞106的边界层流动，壁面模化的大涡模拟方法要将网格量控制在O（Re），对工程应用才有实际意义。Piomelli[12］将 壁 面 模 化 方 法 划 分 为：①壁 面 模 型，例如Schumann[13］提 出 的 平 衡 层 模 型；②在 壁 面 附近单独求解边界层方程的分区方法[14］；③RANS/LES 混合方法，例如DES 类方法[15］。

入流生成方法方面，在壁面附着流动中，层流边界层和转捩区的计算成本甚至是湍流区的10～100 倍，如果只关注湍流区域，需要准确刻画湍流入流。目前采用的入流生成方法有“回收”方法[16-17］、人工合成湍流方法[18］等。

在非结构网格应用方面，由于生成非结构网格相对省时省力，基于非结构网格的LES 方法开始在复杂工程问题中获得越来越多的应用，例如Forsythe 等[19］利 用 非 结 构 求 解 器 实 现 了F-15E全机外形的DES 模拟。但是传统非结构求解器的空间离散精度只有二阶，因而基于间断伽辽金（Discontinuous Galerkin， DG）、有 限 谱 体 积（Spectral Volume， SV）等高精度求解的LES 方法是目前的研究热点[20］。

在工程应用方面，虽然一些商业软件中已有LES 计算模块，但是实际应用还不成熟，还处于从“算法”向“应用”的过渡阶段。由于工业设计部门缺乏对湍流非定常和多尺度效应的正确认识，在尝试应用LES 时，误认为仅将RANS 方法的湍流模式改为LES 方法的亚格子模型，就可以达到可观的效果。实际上，LES 紧密依赖于所采用的数值格式、网格、初边值条件等因素，这些因素间要互相匹配才能开展LES 模拟，不能简单地“一键化”操作。

综上所述，由于存在种种尚待解决的问题，LES 方法还难以像RANS 方法那样成熟地开展批量工程应用，更大程度上还处于方法基础研究、应用基础研究阶段。在商业软件以外，大量基础研究者更多地是采用自己编写的课题组代码、“in-house”代码开展研究。

在国内，由于此前长期缺乏共享的自主CFD软件框架，众多研究者在开展LES 方法研究中，将大量精力耗费在开发前后处理接口、计算格式、并行计算等重复性工作上，力量难以向计算模型、流动机理等更为根本的方向聚焦。

风 雷 软 件（PHengLEI）[21-22］，是 中 国 空 气 动力研究与发展中心研发的、具有自主知识产权的CFD 软件，历经十余年发展，已成为唯一一款能同时支持结构、非结构网格的大型CFD 软件平台。在国家数值风洞工程（NNW）的支持下，风雷软件致力于面向中国研究者提供高可扩展性的CFD 软件基础设施，共同推进中国CFD 软件生态建设，于2020 年12 月面向全国开源，在互联网“红山开源平台”开放代码（平台网址https：∥osredm.com）[23］。

LES 模型是风雷软件开源框架中的重要组成部分，旨在于为国内开展LES 基础和应用研究的学者，提供高起点工具，已在PHengLEI v2112版本中开源。主要功能包括：基于结构/非结构二阶精度有限体积方法的LES 模型，基于结构高阶精度有限差分方法的LES 模型，基于Fourier谱/有限差分混合方法的LES 模型，以及LES 模拟中常用的亚格子模型、初边值条件、非定常湍流统计等方法。

本文主要介绍风雷软件开源框架LES 模型的理论方法、软件设计和算例验证。首先给出LES 的理论方法，然后介绍设计的软件框架，最后通过不可压缩槽道湍流、亚临界雷诺数圆柱、NACA0012 翼型临界攻角的低频振荡等标准算例，给出软件的验证结果。

1 理论方法概述

不可压缩流动和可压缩流动的求解方法不同，采用投影法求解不可压缩流动，空间离散采用Fourier 谱与高阶有限差分相结合的混合方法；采用二阶有限体积和高阶有限差分方法求解可压缩流动。下面对这两类流动求解方法分别作简要介绍。

1.1 基于Fourier 谱/有限差分的投影法

投影法（Projection Method）也称作分步法（Fractional Step Method），由Chorin[24-25］在20 世纪60 年代末提出，最早认为在时间方向上只有一阶精度，后来许多学者发展了各种改进的投影法，将时间方向提高为二阶精度[26-27］。

1.1.1 投影法

无量纲后的非定常不可压缩流动的控制方程为

对流项采用二阶精度的Adams-Bashforth 格式，时间导数项和黏性项采用Crank-Nicholson格式离散[26］，控制方程离散为

2）投影步。根据Helmholtz-Hodge 分解定理，u*可分解为

也即ϕ 要满足泊松方程

求出ϕ 后，压力由式（8）求得

投影步结束后式（9）成立

3）壁面散度修正步。由式（7）求得的ϕ 只能保证u**在壁面的法向分量为0，切向分量不能保证为0。为此，在利用式（5）求速度u**时加入无滑移边界条件

这样由式（10）求得的速度u**在壁面上散度不为0。为此，采用影响矩阵法对壁面散度进行修正，具体不再详述，可参考文献[28］。

1.1.2 Fourier 谱/有限差分混合方法

从以上的分析可看出，本文采用投影法离散控制方程后，需要求解两种不同边界条件类型的泊松方程，第1 种是包含Dirichlet 边界条件的泊松方程

对于槽道湍流，流向和展向均为周期边界，可以采用Fourier 级数展开，法向采用差分方法，用x、y、z 分别表示流向、展向、法向，则速度和压力分别为

式中：x=(x，y，z)T；kx、ky分别为流向波数和展向波数；k=(kx，ky)T。利用Fourier 基 函数的正交性，算子∇2可以离散为

这样，对kx、ky，式（11）、式（12）就转换为z 方向的一维二阶微分方程。z 方向的离散采用Gamet 等[29］发展的非均匀网格空间导数求解方法，得到空间二阶导数的一般形式为

非线性项(u·∇)u 的计算采用“伪谱”方法，并利用3/2 规则来消除混淆误差，具体可参考文献[30］。

式（12）的求解也采用上述方法。

1.2 二阶有限体积和高阶有限差分方法

对三维可压缩NS 方程采用密度加权的Favre 滤波，得到LES 控制方程为

式 中：δij为Kronecker 符 号；μl为 层 流 黏 性 系 数；Prl为层流普朗特数；Cp为定压比热容。式（17）中上标“SGS”表示亚格子项为黏性应力的非线性项为亚格子黏性性扩散项为热通量的非线性项，这3 项通常都被忽略[31］。一般关注的是亚格子应力张量和亚格子热通量项，通过采用亚格子模型使之封闭，亚格子湍流扩散项进行线性化处理[31］

二阶求解器采用结构或非结构的有限体积方法[21］，无黏项采用Roe 格式计算，黏性项采用二阶中心型格式。高阶求解器采用基于结构网格的高精度有限差分方法[32］，无黏项采用WCNS格式[33］，黏性项采用四阶中心型格式。时间推进均采用LU-SGS 隐式方法求解，非定常计算均采用双时间步法[34］。

1.3 亚格子模型

主要采用Smagorinsky 模型、动态Smagorinsky 模型、Sigma 模型来模化亚格子项。

1）Smagorinsky 模型。Fourier 谱/有限差分方法LES 求解器采用原始不可压缩形式的Smagorinsky 模型（Smagorinsky Model， SM）[35］

有限体积/有限差分LES 求解器采用Yoshizawa[36］提出的形式

式中：Prt为湍流普朗特数

2）动 态Smagorinsky 模 型。Fourier 谱/有限差分方法LES 求解器采用原始不可压缩形式的动态Smagorinsky 模型（Dynamic Smagorinsky Model， DSM）[37］，模型系数在水平面平均以提高数值稳定性

有限体积/有限差分LES 求解器采用Lu等[39］提出的形式

3）Sigma 模型。Nicoud 等[11］提出的Sigma模型满足O(y3)壁面渐进特性，在刚性转动、纯剪切、单纯轴对称、单纯各向同性膨胀/收缩流动或者二维流动中可以退化为0。Fourier 谱/有限差分方法LES 求解器采用的模型方程为

式中：Cσ为模型系数，根据各向同性衰减湍流算例的标定，取为1.5；σ1～σ3为速度梯度张量gij的奇异值，并且σ1≥σ2≥σ3，σ1～σ3的具体求法可参考文献[11］。

2 软件架构设计

风雷软件设计了具有良好通用性、可扩展性的体系结构和数据结构，在同一个软件平台上，能同时支持结构和非结构网格（算法）、二阶和高阶精度（算法）。风雷软件LES 模块提供了一个开放平台，可使国内的LES 研究人员从前后处理接口、通量格式、时间离散格式等重复开发中解放出来，将精力聚焦于学科前沿的创新研究，为更多有志于进入这一领域的学者和团队提供高水平的起点，为需要应用LES 方法开展基础流动问题和工程应用问题的学者和团队提供高效高精度的开放平台。

风雷软件LES 模拟同时包含松/紧耦合策略。紧耦合策略，是在二阶结构求解器、二阶非结构求解器、高阶结构求解器上集成了LES 模型，统称为“有限体积/有限差分方法LES 求解器”；松耦合策略，是结合Fourier 谱方法和有限差分方法，开发的求解不可压缩槽道流动的功能模块，称为“Fourier 谱/有限差分方法LES 求解器”。

风雷软件整体框架可参考文献[21-22］，这里不做详细介绍，仅详细介绍与LES 方法相关的软件框架设计。

2.1 LES 计算框架设计

对于松耦合策略，设计的Fourier 谱/有限差分方法LES 求解器计算框架如图1 所示。计算框架由前处理、迭代流程、后处理3 个模块构成。前处理包括网格/参数读入、初始化物理空间/波数空间；迭代流程中每个迭代步都要遍历所有波数；后处理包括流场变量在波数空间的统计输出、流场变量在物理空间的统计输出等。

图1 Fourier 谱/有限差分LES 求解器的计算框架Fig.1 Design diagram of Fourier spectrum/finite difference solver computing framework

Fourier 谱/有限差分方法LES 求解器的功能模块分层设计如图2 所示，也按照内核层、算法层、功能层和应用层进行分层构建。在内核层，复用了风雷软件的计算参数读取，在原有面向实数的数据结构基础上，进一步设计了复数数据结构，采用P3DFFT[40］进行并行Fourier 变换；在算法层，抽象出物理空间计算域和波数空间计算域，设计了高阶紧致有限差分格式和滤波函数；功能层包括微分算子、求解控制流程、前后处理、工具类等。微分算子方面，构建了拉普拉斯算子、梯度算子、散度算子等微分算子模块。前后处理方面，构建了流场变量在波数空间和物理空间之间的转换功能模块，以实现流场数据的可视化。求解控制流程方面，设计了对流步、投影步和壁面散度修正的投影法求解流程。工具类方面，构建了添加速度脉动的模块等；在应用层，利用功能层的拉普拉斯算子、梯度算子和散度算子等，构建了泊松方程求解器。湍流求解不再作为单独的求解器，而是封装为亚格子模型。泊松方程求解器和亚格子模型结合，拓展为Fourier 谱/有限差分方法LES求解器。

图2 Fourier 谱/有限差分方法LES 求解器的功能模块分层设计示意图Fig.2 Functional module hierarchical design of Fourier spectrum/finite difference solver

对于紧耦合策略，设计的有限体积/有限差分方法LES 求解器计算框架如图3 所示。计算框架由前处理、迭代流程、后处理3 个模块构成。前处理包括网格/参数读入、网格转换/分区、求解器加载等；迭代流程由“迭代控制器（Controller）”控制。

图3 有限体积/有限差分LES 求解器的计算框架Fig.3 Design diagram of finite volume/finite difference solver computing framework

首先根据Zone 的信息初始化每个Zone 上的所有求解器。然后开始迭代计算，在每个迭代步内包括2 层循环遍历：第1 层遍历不同求解器，第2 层是在每个求解器中遍历每个Zone；后处理包括湍流一阶/二阶矩的统计平均、Fourier 分析、模态分析等工具包。

对于有限体积/有限差分LES 计算，每个Zone 上加载的求解器包括NS 方程求解器NSSolver 和有限体积/有限差分LES 求解器LESSolver。对原用于进行RANS 流动模拟的NS 方程求解器NSSolver 作细微改造：将湍流黏性通量修改为反对称项和对称项2 部分，与SGS 应力项的对称项和反对称项相对应。

LESSolver 的功能模块分层设计如图4 所示，与风雷软件的RANS 湍流模式方程求解器TurbSolver 类似，按照内核层、算法层、功能层、应用层进行分层构建。由于软件现有的亚格子模型均为代数形，依赖当地的网格尺度、速度梯度张量等信息，不需要求解模型方程，因而在功能层的求解控制流程模块删除黏性项、对流项等求解过程，在算法层增加滤波函数、壁面函数等模块。风雷软件原有数据通信模块采用异步通信模式，可以减少通信次数，但会影响数值稳定性，LESSolver 在求解SGS 应力项前增加一次速度梯度张量的计算和数据通信，以提高数值稳定性。后处理模块增加湍流统计输出功能。

图4 有限体积/有限差分LES 求解器的功能模块分层Fig.4 Functional module hierarchical design of finite volume/finite difference solver

2.2 LES 求解器设计

风雷软件将几何计算域Zone 与求解器Solver 作为数值计算的基础。Zone 是框架的核心，负责存储网格、加载求解器、存储流场变量等，每个Zone 上可以有多个网格块Grid，每个Grid 既可以是结构网格也可以是非结构网格。根据计算任务，每个Zone 上可以分别加载不同的Solver[22］。

将不同Solver 的共性提取出来抽象为求解器基类，从基类派生出具有差异化的求解器子类。如图5 所示，由基类派生出的CFD 求解器类CFDSolver，其中定义了CFD 求解器的共性成员和接口，如计算网格、空间离散、时间推进、边界条件处理等纯虚函数接口。

SpecDiffHybSolver 类 是Fourier 谱/有 限 差分求解器，由于所用的空间离散和时间推进格式与传统基于有限体积方法的CFD 求解有很大不同，因此直接从Solver 基类派生。

原始CFDSolver 派生得到NS 方程求解器类NSSolver、湍流模式方程求解器类TurbSolver。由于LES 所采用的亚格子模型多数为代数形，不需要求解模式方程，因此直接从CFDSolver 派生出有限体积/有限差分LES 求解器类LESSolver。

LESSolver 又可以派生出基于不同网格类型的求解器类：基于结构网格的LESSolverStruct和基于非结构网格的LESSolverUnstruct。NSSolverStruct 又派生出结构网格高精度求解器类NSSolverStructFD，而基于NSSolverStructFD的大涡模拟求解器类被融合在LESSolver-Struct 中。

LES 数值模拟流场数据可供气动声学、人工智能等领域专家使用，对此，采用CGNS（CFD General Notation System）数据底层所采用的HDF5（Hierarchical Data Format）标 准 数 据 格式，以保证数据的可扩展性。相关格式见软件用户手册[41］。

2.3 并行计算模式设计

Fourier 谱/有限差分方法LES 求解器是对泊松方程式（12）、式（13）在谱空间下进行求解，需要对所有流向波数kx和展向波数ky的遍历，任意波数对（kx，ky）的求解与其他波数无关，因而理论上所有波数对的求解是完全独立的。然而对流项在“伪谱”方法中是通过变换到物理空间求解的，这个过程的并行计算需要并行快速Fourier变换（Fast Fourier Transforms， FFT）。因此，高效的并行快速Fourier 变换对整个求解器的并行效率和可扩展性有决定性的影响。

Fourier 谱/有限差分方法LES 求解器需要对数据在2 个维度各进行一次FFT，传统并行方法是把数据只在其中一个维度分布到n个进程。以4 进程并行计算三维槽道为例，如图6（a）所示，需要在x方向和z方向各进行一次FFT。首先，将数据在z方向分为4 份，分配到进程1～4，使得每个进程中的数据在x方向是连通的，这样每个进程就可以在x方向进行FFT；然后，将上一步变换后的数据在x方向分为4 份，重新分配到进程1～4，使得每个进程中的数据在z方向是贯通的，这样每个进程就可以在z方向进行FFT。这个方案仅能在一个方向上划分计算域，称为一维分解。该方案计算网格块不能进一步细分，限制了其并行粒度，并行规模也难以增加。

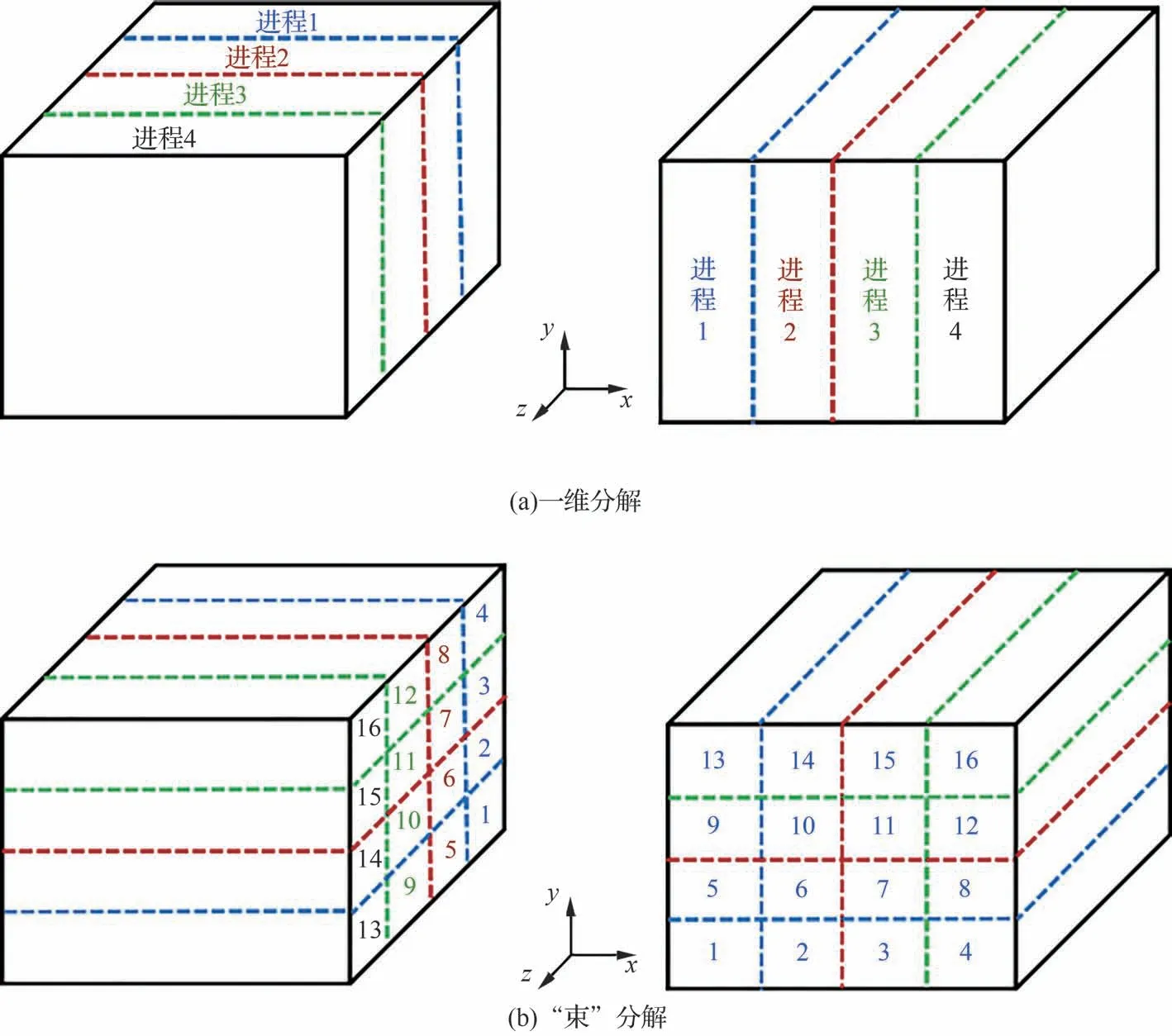
图6 并行快速Fourier 变换：一维分解和“束”分解Fig.6 1D and pencils decomposition of parallel FFT computations

近年来，加州大学开发了一款开源工具P3DFFT[40］专 门 处 理 并 行Fourier 变 换，可 将 需要进行FFT 的数据在其中一个维度分布到n1组，同时将不需要变换的维度分布到n2组。以16 进程并行计算三维槽道为例，如图6（b）所示，需要在x方向和z方向各进行一次FFT。首先，将数据在y方向和z方向同时分为4 份，分配到进程1～16，使得每个进程中的数据在x方向是贯通的，这样每个进程就可以在x方向进行FFT；然后，将上一步变换后的数据在x方向和y方向各分为4 份，重新分配到进程1～16，使得每个进程中的数据在z方向是贯通的，这样每个进程就可以在z方向进行FFT。这个方案可以2 个方向上划分计算域，称为二维分解或者“束”分解（Pencils Decomposition）。本文采用“束”分解。

并行策略方面，有限体积/有限差分方法LES 求解器的并行计算流程与风雷软件基本一致：当一种求解器类型的计算执行完成后，每个分区之间执行一次并行通信，同时在分区内部网格间执行一次边界面数据交换。当求解器列表遍历完成后，也要进行求解器之间的数据通信，以实现不同求解条件下流场或特殊边界的数据传递和交换[34］。

通信模式方面，采用了基于循环遍历所有网格块的模式进行通信：每个进程均遍历所有网格块（仅仅是块编号），当所遍历的网格块属于当前进程时，则向邻居网格块所在进程发送数据；当所遍历的网格块属于其邻居网格块时，则从邻居网格块所在进程接收数据，详细参考文献[21］。

3 算例验证

采用不可压缩槽道湍流、亚临界雷诺数圆柱绕流、NACA0012 临界攻角的低频振荡等3 个算例，对本文设计的Fourier 谱/有限差分方法LES求解器、有限体积/有限差分LES 求解器进行验证。

3.1 不可压缩槽道湍流

不可压缩槽道湍流由于外形简单且流动现象单一，是研究壁面剪切流动的标准算例，也是考量数值方法和亚格子模型的基础算例，使用本算例可以考核本文设计的Fourier 谱/有限差分方法LES 求解器。谱方法是数值误差最小的一种离散方法，因此是考察亚格子模型误差的最理想方法。

图7 是不可压缩槽道湍流算例，计算域大小为Lx×Ly×Lz=2πh×2h×πh（h是槽道半高度），x和z方向是周期边界条件，y方向是无滑移壁 面，雷 诺 数Reτ=uτh/ν=395（uτ为 壁 面 摩 擦速度）。

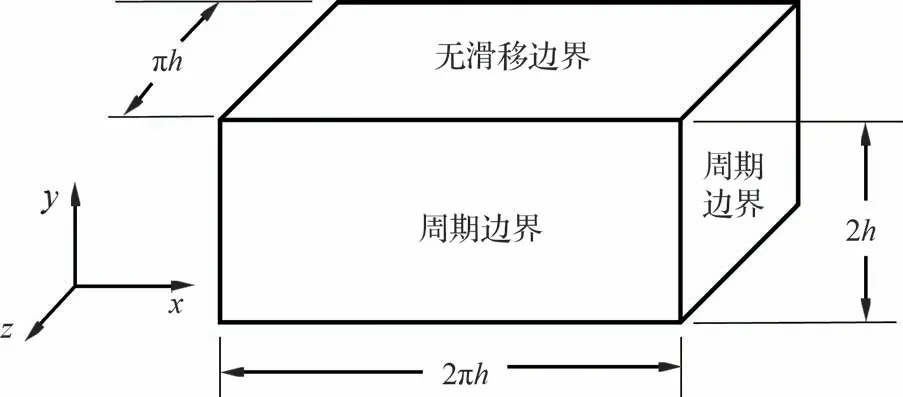
图7 不可压缩槽道湍流的示意图Fig.7 Incompressible turbulent channel flow

对该算例，通常做法是在流向（x方向）、展向（z方向）采用Fourier 谱方法，在法向（y方向）采用基于Chebyshev 多项式的谱方法[42］。而本文在法向采用高阶有限差分方法，这是因为，若在法向采用基于Chebyshev 多项式的谱方法，则要求网格点分布必须满足Chebyshev 多项式关系，这极大地限制了在高雷诺数流动中的应用，而本文在法向采用高阶有限差分方法，可打破这一限制，比传统方法更具优势。

算例A～算例D 采用不同的亚格子模型和网格 尺 度，计 算 结 果 与Moser 等[43］的DNS 结 果、Nicoud 等[11］的LES 结果对比。算例A～算例D和文献中采用的数值方法、计算域、网格、亚格子模型如表1 所示，Nx、Ny、Nz为3 个方向的网格数目，Δx+、Δy+、Δz+为无量纲化后的网格尺度。算例A 与Moser 等[43］的DNS 算例采用完全相同的计算域和网格尺度，只是数值方法不同，用于考核Fourier 谱/有限差分方法LES 求解器的数值精度。法向网格为双曲正切分布，流向和展向网格均匀分布，Moser 等[43］在流向和展向离散采用与算例A 相同的Fourier 谱方法，法向采用Chebyshev 多项式。算例B～算例D 采用了不同的亚格子模型，Smagorinsky 模型系数CS=0.1，引入van Driest 函数修正壁面附近的涡黏系数，Sigma模型系数Cσ=1.5。Nicoud 在所有方向均采用四阶中心Taylor-Galerlin 有限元格式。算例B～算例D 流向和法向网格尺度比Nicoud 算例更小，展向网格尺度相当，足以满足LES 模拟需求[3］，用于验证Fourier 谱/有限差分方法LES 求解器具备考核亚格子模型的能力。

表1 本文算例和文献采用的数值方法、计算域、网格和亚格子模型Table 1 Numerical methods， computational domain， grid and subgrid models used in this paper and references

将计算结果作时间平均和空间平均，得到平均流向速度剖面（见图8）、平均雷诺应力分布（见图9），横纵坐标都采用壁面坐标。可以看到，算例A 的平均流向速度剖面、雷诺应力分布都与Moser 等[43］的基本一致，说明本文设计的Fourier谱/有 限 差 分 方 法LES 求 解 器 与Moser 等[43］的DNS 求解器数值精度相当，法向采用高阶有限差分方法并没有降低数值精度。Chebychev-tau 离散方法受限于Chebychev 配置点的布置，而高阶有限差分方法对于网格点的布置没有限制，这是本文设计的Fourier 谱/有限差分方法LES 求解器的一大优势。

图8 平均流向速度剖面Fig.8 Mean streamwise velocity profile

图9 平均雷诺应力分布Fig.9 Mean Reynolds stress profile

算例B～算例D 的平均流向速度剖面与Moser 等[43］的DNS 结果基本一致。对算例C，与Nicoud 等[11］利 用DSM 模 型 得 到 的 速 度 剖 面 相比，更 接 近Moser 等[43］的DNS 结 果，这 是 由 于Nicoud 等[11］的DSM 动态模型系数是通过局部平均得到的，而算例C 的动态模型系数是在水平方向平均得到的。

算例B 的流向雷诺应力峰值略小于DNS 结果，在其他位置与DNS 结果基本一致，这可能是由于Smagorinsky 模型不满足O(y3)的近壁特性。算例C 的流向雷诺应力峰值略小于DNS 结果，是由于LES 方法只解析部分雷诺应力，剩余部分雷诺应力由亚格子模型模化；而Nicoud 等[11］利用DSM 模型得到的流向雷诺应力峰值略大于DNS 结果，可能是由于数值误差和模型误差相互抵消导致的，其使用的有限差分方法数值误差可能偏大，网格也可能略稀疏。算例B～算例D 的法向、展向雷诺应力与Moser 的DNS 结果基本一致，并且比Nicoud 的LES 结果更接近Moser 的DNS 结果，进一步说明了Nicoud 的数值误差过大。

通过以上分析，本文设计的Fourier 谱/有限差分方法LES 求解器具有与Fourier-Chebychev方法相当的数值精度，在验证亚格子模型时可以排除数值误差的影响。

3.2 亚临界雷诺数圆柱绕流

Re=3 900 条件下的圆柱绕流处于亚临界状态，分离前的边界层为层流，分离后的剪切层逐渐失稳，尾迹呈现三维湍流特性，是用于考核钝体绕流模拟能力的经典算例。采用不同精度、不同网格类型的LES 求解器和不同的亚格子模型，对该算例进行考察，主要为验证不同类型的LES求解器和亚格子模型的可靠性。

计算域和网格如图10 所示，x、y分别为流向、法向，r、θ分别为径向、周向，展向计算域大小为πD（D为圆柱直径）。圆柱表面是无滑移边界，展向是周期边界，其他均是远场边界。采用“O”型网格，网格分布为Nr×Nθ×Nz=434×264×48，周向有128 个点集中分布在尾迹区中心线两侧90°范围内，展向网格均匀分布。

图10 亚临界雷诺数圆柱绕流计算域和网格Fig.10 Computation domain and its grid of flow past circular cylinder at sub-critical Reynolds number

设计了E～算例H 4 个算例（见表2），分别采用了不同网格类型、数值精度的求解器和不同的亚格子模型，以全面考核本文设计的有限体积/有限差分方法LES 求解器。

表2 算例采用的求解器和亚格子模型Table 2 Solvers and sub-grid scale models used in simulations

图11 给出了中心线（y/D=0）平均速度（时间平均和展向平均，用来流速度Uc无量纲化，下同）沿x方向分布，统计平均周期T≈120Tvs（Tvs为涡脱落周期）与文献[44-48］的对比。可以看到，后驻点处的平均速度为0，之后减小到某个极小值，然后逐渐恢复到接近来流速度，中间改变过一次速度方向。定义后驻点与速度改变方向处之间的距离为回流区长度（Lr），与各文献中的回流区长度对比（见表3），可以看到回流区长度范围为1.19D～1.67D。算例E、H 的回流区长度基本在文献结果范围之内，算例F、G 的回流区长度略大于文献结果。

表3 回流区长度对比Table 3 Recirculation lengths comparision

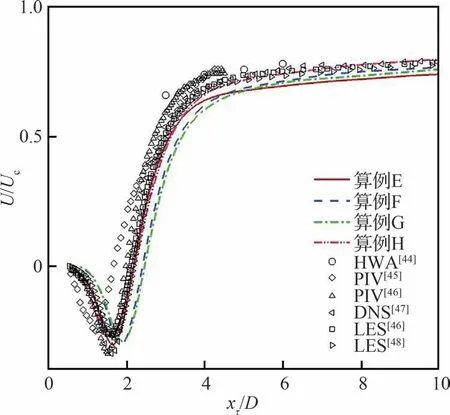
图11 圆柱尾迹区中心线上的平均流向速度分布Fig.11 Mean streamwise velocity in wake centerline

从算例E、F 的Q等值面图（见图12，采用x方向涡量ωx着色）可以看出，层流边界层分离形成二维层流剪切层，随着剪切层失稳，三维涡结构开始出现，流动逐渐过渡到湍流。相较于算例E，算例F 的剪切层在较长的尾迹区内保持二维层流状态，这也是后文中平均速度、雷诺应力分布差异的主要原因。图12（a）标注了近尾迹区的3 个流向站位分别为x/D=1.06，1.54，2.02，以下重点分析这3 个站位的平均速度、雷诺应力分布。

从近尾迹区3 个站位的平均流向速度分布（见图13）看，本文计算结果、文献[45-49］结果都是由U 型速度分布逐渐过渡到V 型速度分布，不同的是过渡点的位置。U 型速度分布对应于层流剪切层，V 型速度分布对应于湍流剪切层。在x/D=1.06 站位，算例E～算例H 都是U 型分布，与文献结果一致。在x/D=1.54 站位，算例E、H 已过渡到V 型分布；而算例F、G 尚未完全过渡到V型分布，说明处于层流剪切层逐渐失稳向湍流剪切层过渡的状态，这也可以从图12 中看出。

图12 圆柱尾迹区的瞬时Q 等值面图Fig.12 Instantaneous iso-surfaces of Qcriterion in wake

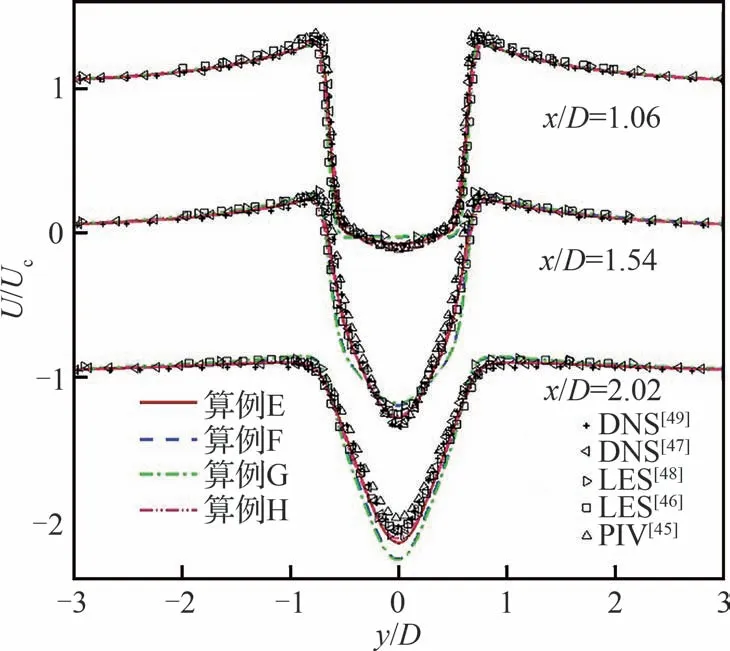
图13 圆柱近尾迹区平均流向速度分布Fig.13 Mean streamwise velocity in near wake

从近尾迹区3 个站位的平均法向速度分布（见图14）看，算例E～算例H 的速度型都有很好的反对称性。在x/D=1.06，2.02 站位，算例E、H 与文献[45-49］中的实验、计算结果符合得很好，算例F、G 的结果与文献结果相比，峰值位置和峰值大小略有差异。在x/D=1.54 站位，文献结果之间有很大的差异，算例E、H 基本处于不同文献结果的中间范围内，之所以有差异，是由于层流剪切层在此处失稳，逐渐过渡到湍流剪切层，是一个中间过渡状态，数值噪声和实验的来流噪声都会对结果有很大影响。

图14 圆柱近尾迹区平均法向速度分布Fig.14 Mean normal velocity in near wake

图15 是近尾迹区3 个站位的流向雷诺正应力u'u' 分布。在x/D=1.06 站位，u'u' 的峰值对应剪切层失稳的位置。在x/D=1.54 站位，主分离涡的出现使得上述峰值附近出现另2 个峰值。随着湍流混合加强，2 个峰值逐渐融合为一个峰值。不同文献之间的雷诺应力大小有很大的差异，本文的计算结果基本在文献[45-49］结果的中间范围内。在x/D=1.06，1.54 站位，算例F、G 的结果要小于算例E、H，这也是由于算例F、G 模拟的剪切层失稳较晚所致。

图15 圆柱近尾迹区3 个站位的流向雷诺正应力分布Fig.15 Mean streamwise Reynolds stress at three locations in near wake

从以上分析可知，算例E、H 的结果基本一致，算例F、G 的结果基本一致，说明亚格子模型对结果的影响很小，数值方法对结果的影响较大。另外，对剪切层失稳的模拟对于速度、雷诺应力等的预测非常关键。剪切层失稳受到数值噪声和实验来流噪声的影响，这使得不同的计算程序和实验条件得到的结果相差很大，从不同文献之间的差异可以看出这一点。对比本文的4 个算例，算例F、G 模拟的剪切层失稳位置在E、H 的上游，发展出湍流剪切层的位置更靠上游，速度型分布与文献结果也更为接近，这可能是由于二阶精度方法的数值误差与亚格子模型误差共同作用导致的。

3.3 NACA0012 临界攻角的低频振荡

临界攻角下的翼型绕流伴随着流动分离、剪切层失稳、转捩、流动再附等复杂的非定常流动现象，是体现高精度LES 方法优势的一类流动问题。Zaman 等[50］在实验中发现临界攻角状态下的流动除了涡脱落模态，还存在着一个更低频的流动 模 态。Almutairi 和Alqadi[8］利 用LES 方 法 对NACA0012 翼型的低频振荡现象进行了数值模拟，认为后缘涡脱落引起的声波激发了前缘剪切层，使剪切层失稳并转捩，湍流剪切层再附又抑制了后缘涡脱落。这样，后缘分离涡与前缘剪切层共同构成的反馈机制，是低频振荡现象的原因。Eljack 和Soria[51］的LES 计 算 结 果 发 现 前 缘 附 近存在的“三涡”结构导致了流动处于周期性的分离和附着状态，使得流动存在着低频振荡现象。

选取攻角α=9.29°的NACA0012 翼型作为研究对象，马赫数Ma=0.4，基于翼型弦长c的雷诺数Rec=50 000，计算域Lx×Ly×Lz=21c×20c×0.5c。网格如图16 所示，壁面法向第1 层网格Δy+w＜0.35，流动分离、转捩区的流向网格间距Δx+＜30，展向均匀布置96 个网格点，展向网格间距Δz+＜18，网格总量约为2 600 万，满足LES 方法对网格尺度的要求[3］。无量纲时间步长为ΔtU/c=0.002，采用400 核，模拟了20 万个无量纲时间步长。

图16 NACA0012 计算网格Fig.16 Computation grid of NACA0012

图17 是模拟得到的瞬时Q等值面图（采用x方向涡量ωx着色），图中可以看到层流剪切层失稳、转捩和三维涡结构产生的过程。

图17 NACA0012 绕流瞬时Q 等值面图Fig.17 Instantaneous iso-surfaces of Q criterion around NACA0012

图18 是升力系数（CL）随时间的变化曲线，图中可以看出升力系数的振动幅值与平均值相当，流动状态在附着流动与失速间交替。对升力系数的时间序列利用现代谱估计方法得到功率谱密度（Power Spectrum Density，PSD）[52］，如图19所示，计算得到的升力系数功率谱的第一峰值对应的斯特劳哈尔数St=fcsinα/U=0.005 5，与Almutairi 和Alqadi[8］得 到 的 峰 值 位 置St=0.005基本一致，峰值大小也基本一致。

图18 升力系数的时间变化曲线Fig.18 Time history and power spectrum of lift coefficient

图19 升力系数的功率谱密度Fig.19 Power spectrum density of lift coefficient

4 结 论

基于风雷软件开源框架，分别采用松耦合和紧耦合的模式，开发了Fourier 谱/有限差分方法LES 求解器和有限体积/有限差分方法LES 求解器。初步实现了基于结构网格和非结构网格，基于二阶有限体积方法、高阶有限差分方法和Fourier 谱方法的LES 功能。集成了多种亚格子模型、初边值条件和非定常湍流统计功能。

分别采用不可压缩槽道湍流、亚临界雷诺数圆柱绕流、NACA0012 临界攻角的低频振荡3 个算例，对所设计的开源求解器进行验证。计算表明，Fourier 谱/有限差分方法的LES 求解器对于不可压缩槽道湍流的模拟结果与DNS 结果一致，数值精度与Fourier-Chebychev 方法相当，在考核亚格子模型时可以排除数值误差的影响。有限体积/有限差分方法的LES 求解器对于亚临界雷诺数圆柱绕流算例的模拟结果与文献中的计算和实验结果基本一致，证明了有限体积/有限差分方法的LES 求解器和几种亚格子模型的可靠性。高阶精度有限差分方法的LES 求解器复现了NACA0012 临界攻角的低频振荡现象，St数值与文献中基本一致，体现了高阶精度有限差分方法的LES 求解器对于复杂湍流模拟的能力。

以上代码、接口和算例均已在风雷软件PHengLEI 2112 版本中开源，可以在“红山开源平台”下载。LES 模块和软件框架的接口，可参考文献[21-22］，或者用户手册[41］，受篇幅限制，这里不再述及。

下一步，将在以下方面持续开展软件功能开发和优化：①壁面模型方面，集成WMLES、RANS/LES 混合方法等；②集成人工合成湍流功能；③发展多层次、多维度的混合计算方法，例如结构/非结构网格混合计算方法，二阶精度/高阶精度混合计算方法，RANS/LES 混合计算方法等。

致 谢

本项研究得到了中国空气动力研究与发展中心计算空气动力研究所风雷课题组和马燕凯、闵耀兵等的大力支持，在此表示感谢。