非线性欠驱动不稳定系统的自耦PID控制方法
2023-04-19熊屹林曾喆昭
熊屹林, 曾喆昭, 王 伟
长沙理工大学, 长沙 410076
0 引 言
非线性欠驱动不稳定系统广泛存在于航空航天、地质勘探、国防军事等领域,一直是国内外控制领域学者关注的重点[1-6].目前,非线性欠驱动不稳定系统的控制方法主要有:比例-积分-微分(proportional-integration-differential,PID)控制方法[7-8]、线性二次型(linear-quadratic-regulator, LQR)最优控制方法[9-12]、模糊控制方法[13-14]、滑模变结构控制方法[15-17]、自抗扰控制方法[18-20]等.尽管现有这些控制方法都获得了有效的控制效果,然而却存在各自的局限性:如PID控制方法尽管结构简单,却存在增益鲁棒性差与抗扰动鲁棒性差的问题,对非线性时变系统控制而言,其控制效果较差;LQR最优控制方法不仅依赖于精确的被控系统模型,而且计算量大,不便于实际应用;模糊控制方法尽管不依赖于被控对象模型,然而对积分环节无法建立模糊规则,稳态控制精度不高;滑模变结构控制方法尽管不依赖于被控对象模型,控制器的增益鲁棒性与抗扰动鲁棒性都较好,然而却存在固有的高频抖振现象,不利于执行机构,而且控制精度不高;为了抑制滑模控制的高频抖振现象,则需要增加幂次趋近律或双幂次趋近律,因而增加了控制系统的复杂性;自抗扰控制方法尽管不依赖于被控对象模型,控制器的增益鲁棒性与抗扰动鲁棒性都较好,然而涉及的控制器参数较多、控制器结构复杂、计算量大、难以分析控制系统的稳定性.
为了解决现有控制方法存在的各种局限性问题,本文拟使用ACPID控制理论方法[21-22].曾喆昭教授认为:PID的比例、积分、微分3个不同环节都与误差有关,三者之间一定存在内在的必然关系,而不是相互独立的关系,因而提出了以速度因子为核心联系因子的ACPID控制理论方法[21],科学建立了基于速度因子的PID增益镇定规则(量纲换算规则),解决了传统PID增益鲁棒性差与抗扰动鲁棒性差的问题.然而,文献[21]只是定性质疑PID存在理论问题,没有科学解释引起PID存在增益鲁棒性差与抗扰动鲁棒性差的理论根源.为此,曾喆昭教授在文献[22]中根据PID控制系统的物理属性分析,发现了传统PID因无量纲的比例增益形成的控制力只具有广义位移的量纲属性,而任意一阶线性或非线性系统的控制输入则要求广义速度的量纲属性;任意二阶线性或非线性系统的控制输入则要求广义加速度的量纲属性,以此类推,因而传统PID形成的控制力与任意一阶或二阶被控系统的控制输入之间的同一物理量却存在量纲冲突的矛盾,而且还发现了无量纲的比例增益引起PID比例、积分、微分等3个不同环节形成的控制力在控制过程中存在相互独立的不协调控制的矛盾.作者认为曾喆昭教授在文献[22]中科学发现并解释了无量纲比例增益是引起PID存在增益鲁棒性差与抗扰动鲁棒性差的理论根源,创造了ACPID控制理论[21],提出了遵循量纲匹配规则的控制理论方法.与现有控制方法相比,ACPID控制理论方法的主要优势如下:
1) ACPID控制器不仅保留了PID控制器结构简单的优势,而且只根据一个速度因子的镇定数值即可形成比例-积分-微分等3个增益的镇定规则,简单实用.
2) 由过渡过程时间tr来镇定速度因子,简单实用[22]:①ACPID的速度因子镇定规则:zc=10α/tr,1<α<10;②ACPD (auto-coupling proportional-differential)与ACPI (auto-coupling proportional-integration)的速度因子镇定规则:zc=20α/tr,1<α≤10.
3) ACPID包括ACPD与ACPI控制系统具有良好的鲁棒稳定性和良好的抗扰动鲁棒性.
4) ACPID控制理论通过总扰动定义, 可以将任意复杂的非线性系统等价映射为线性扰动系统, 因而淡化了线性与非线性系统分类的概念.
1 问题背景
为了便于理论联系实际,本文以两轮自平衡机器人系统为例,对非线性欠驱动不稳定系统进行理论分析与控制系统设计.两轮自平衡机器人系统模型如图1所示.
该系统由机器人车身本体(包括连接轴、摆杆、负载和直流电机)和左右车轮3个部分组成,在2个独立电机的驱动作用下,左右2个车轮形成独立扭矩,由此构成了一种可以控制平衡、行走、转向的两轮式倒立摆系统.此外,机器人的行走运动与转向运动间的干扰非常小,其侧视图与俯视图如图2所示.
1.1 两轮自平衡机器人数学模型
机器人行走运动与转向运动的数学模型如下[6-12]:
1)行走运动模型
(1)
其中,x=Rθ,T=(TL+TR)/2,m11=(m+M)R+Jw/R,m12=MlR,m22=MlR2+Jb,Gb=Mgl.
2)转向运动模型
(2)
其中,Tδ=TR-TL为机器人转向运动时的等效力矩.
1.2 模型映射
将式(1)和式(2)结合在一起,则可表示为
(3)
由式(3)可知,两轮自平衡机器人系统有3个自由度x、α与δ,而只有2个控制输入T与Tδ,因而是一个典型的非线性欠驱动系统,而且是一个强耦合时变系统.针对该复杂系统的控制问题,现有控制方法遇到的主要问题如下:
1) 传统PID因其增益鲁棒性差与抗扰动鲁棒性差的因素难以独立实现有效控制.
2) LQR最优控制方法需要对非线性系统(3)做线性化处理,并根据线性系统来寻找一个最优状态反馈控制器来达到控制目的.然而,该方法涉及16个参数的镇定,控制系统结构复杂、计算量很大.
3) 自抗扰控制具有良好的鲁棒稳定性和抗扰动鲁棒性,然而该方法涉及参数过多、控制系统结构复杂、计算量很大.
4) 滑模控制具有良好的鲁棒稳定性和抗扰动鲁棒性,然而,该方法存在固有的高频抖振现象,不利于执行机构.为了抑制高频抖振,则要求引入单幂次或多幂次趋近律,使得控制系统结构复杂、计算量大.
(4)
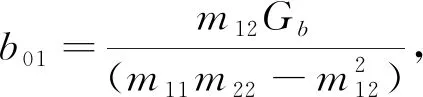
2 ACPD控制系统
ACPID的主要特点在于通过速度因子zc将比例、积分、微分3个不同属性物理环节自行耦合在一起, 进而形成一个功能各异、目标一致的协同控制力[21-22].在忽略积分环节的情况下,本文拟使用ACPD控制方法进行控制系统设计.
2.1 控制系统结构
两轮自平衡机器人控制系统由行走控制和转向控制组成,如图3所示.
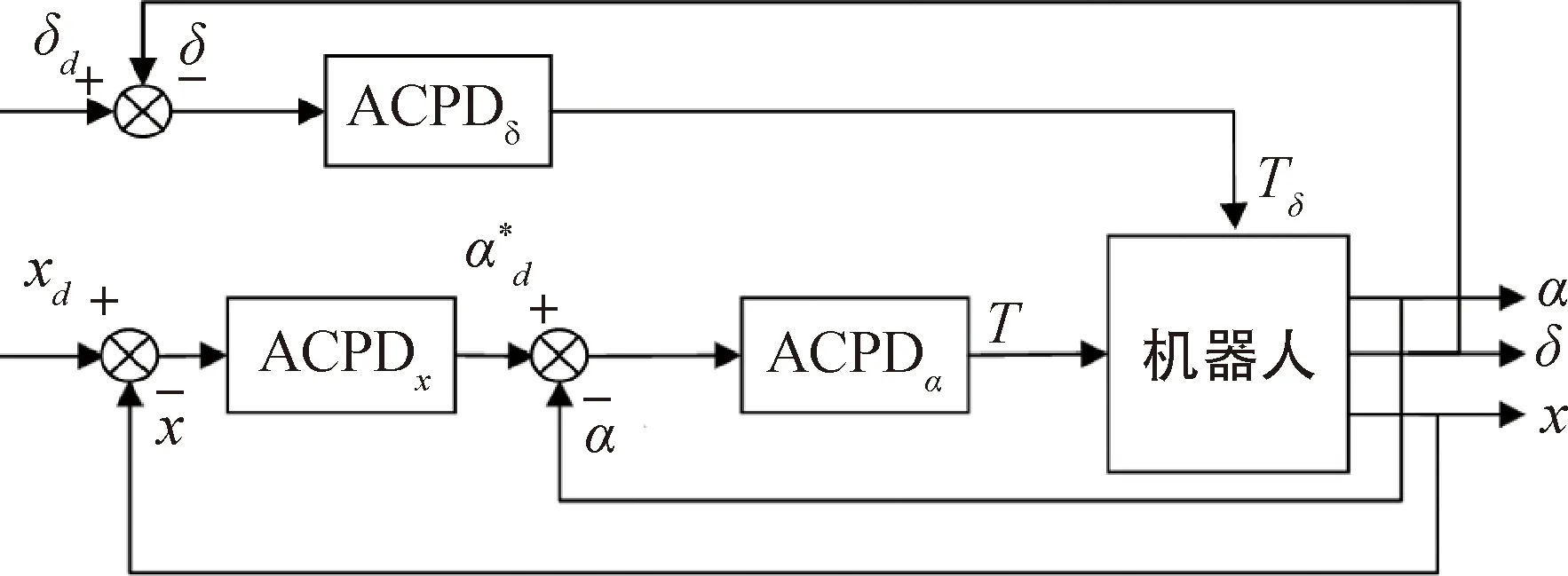
图3 ACPD控制结构示意图Fig.3 ACPD control structure diagram
2.2 行走控制系统
(1)位移环过阻尼ACPDx控制器设计

(5)
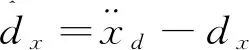
考虑到两轮自平衡机器人系统是一个平衡点不稳定的系统,因而在ACPD控制理论[21-22]的基础上,对微分控制力使用过阻尼的方法来抑制超调与振荡现象,即本文设计的过阻尼虚拟控制器ACPDx为
(6)

(2)倾角环ACPDα控制器设计
(7)
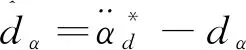
为使受控误差系统(7)的倾角跟踪误差e21趋近稳定的平衡点零点,在忽略积分环节的情况下,根据ACPID控制理论[21-22],本文设计的倾角环ACPDα控制器为
(8)
其中,0 (9) 为使转向控制系统(9)的跟踪误差e31趋近稳定的平衡点零点,在忽略积分环节的情况下,根据ACPID控制理论[21-22],本文设计的转向环ACPDδ控制器为 (10) 其中,0 为了节省篇幅,以上定理的证明请参照文献[21-22],本文不赘述. 考虑到两轮自平衡机器人系统是一个平衡点不稳定的系统,在文献[22]的基础上,本文定义的最小速度因子则为 (11) 其中,1 为了便于比较,取机器人模型参数和初始状态与文献[12]相同,模型参数:M=0.6 kg,m=0.03 kg,R=0.04 m,D=0.14 m,l=0.072 m,g=9.81 m/s2,JW=2.4×10-5kg·m2,Jb=7.5×10-5kg·m2,Jδ=1.1×10-3kg·m2;初始状态:x(0)=0,α(0)=π/18,δ(0)=0. 下列仿真实验中,采样频率为4000 Hz,仿真时间为70 s. 仿真实验1匀速直线运动 图4 匀速直线运动控制结果Fig.4 Uniform linear motion control results 图5 文献[12]控制结果Fig.5 Control results in [12] 比较图4与图5的位置角跟踪误差可知, ACPD控制方法的最大绝对误差小于12 rad,而文献[12]的最大绝对误差则小于30 rad,表明ACPD控制方法的跟踪控制精度是文献[12]的2.5倍. 此外,文献[12]是基于精确模型的状态全反馈控制方法,整个控制系统涉及多达16个控制器参数,结构复杂,计算量大;而本文的3个控制器只需要镇定3个速度因子,且其中的2个速度因子完全相同:z1c=z3c,另一个速度因子则为z2c=(15~25)z1c,因而本文的ACPD控制方法实际上只需要镇定一个速度因子即可,不仅结构简单,便于实际应用,而且不依赖于被控对象的模型. 仿真实验2匀速圆周运动 设机器人做半径为4 m,线速度为4 m/s的匀速圆周运动,则位移期望值xd=4t,转向角期望值δd=t.当z1c=z3c=9,z2c=16z1c=144时,本文使用ACPD控制方法的仿真结果如图6所示,文献[12]的结果如图7所示. 由图6~7可知,本文使用ACPD控制方法,位置角和转向角的最大绝对跟踪误差分别小于8.6 rad和0.02 rad,而文献[12]的则分别小于28 rad和0.28 rad,表明本文的ACPD控制方法获得的跟踪控制精度分别是文献[12]的3倍和14倍,再次表明了本文ACPD控制方法在跟踪控制精度方面具有明显优势. 图6 匀速圆周运动控制结果Fig.6 Uniform circular motion control results 图7 文献[12]控制结果Fig.7 Control results in [12] 针对非线性欠驱动不稳定系统的控制问题,提出了一种基于ACPID控制理论的控制方法.该方法的主要特色是在外环引入一个虚拟控制力来形成内环的虚拟指令,从而使欠驱动的系统等价映射为虚拟全驱动的系统,有效解决了欠驱动系统的控制难题;使用了一种具有良好鲁棒稳定性和抗扰动鲁棒性的ACPD控制方法,并对速度因子模型做了改进;通过引入总扰动概念,使非线性复杂系统等价映射为线性扰动系统,因而淡化了线性系统与非线性系统分类的概念,高度统一了线性系统与非线性系统的控制理论思想.仿真结果表明了本文控制方法的有效性,与文献[12]相比,本文的控制系统结构简单、计算量小、便于实际应用,而且跟踪控制精度更高,在非线性欠驱动复杂系统控制领域具有广泛应用价值.2.3 转向控制系统


2.4 控制系统鲁棒稳定性分析
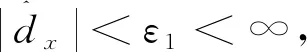
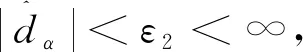

2.5 速度因子镇定
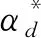
3 仿真分析
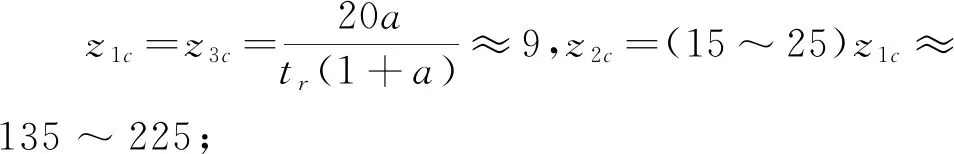


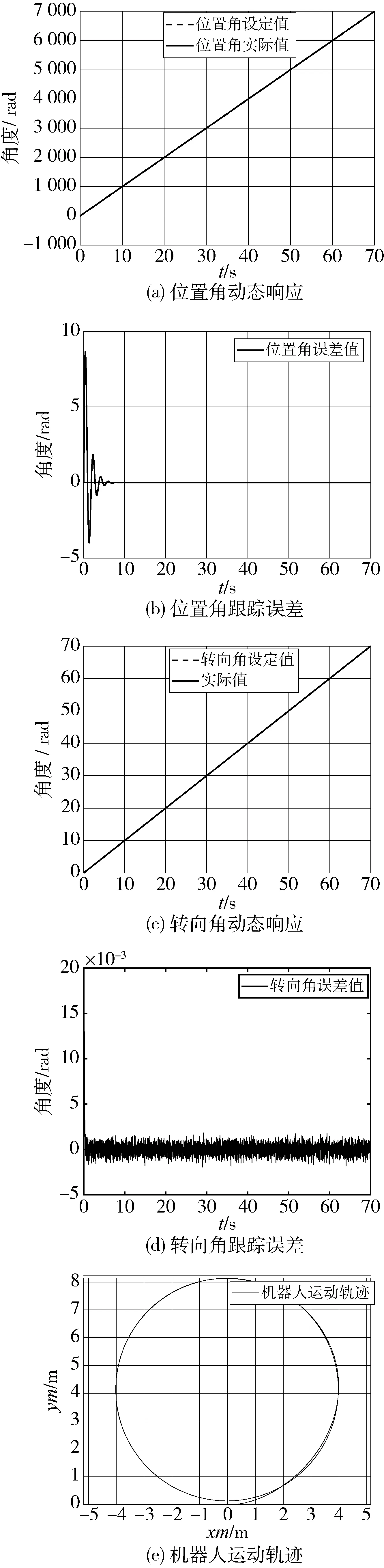
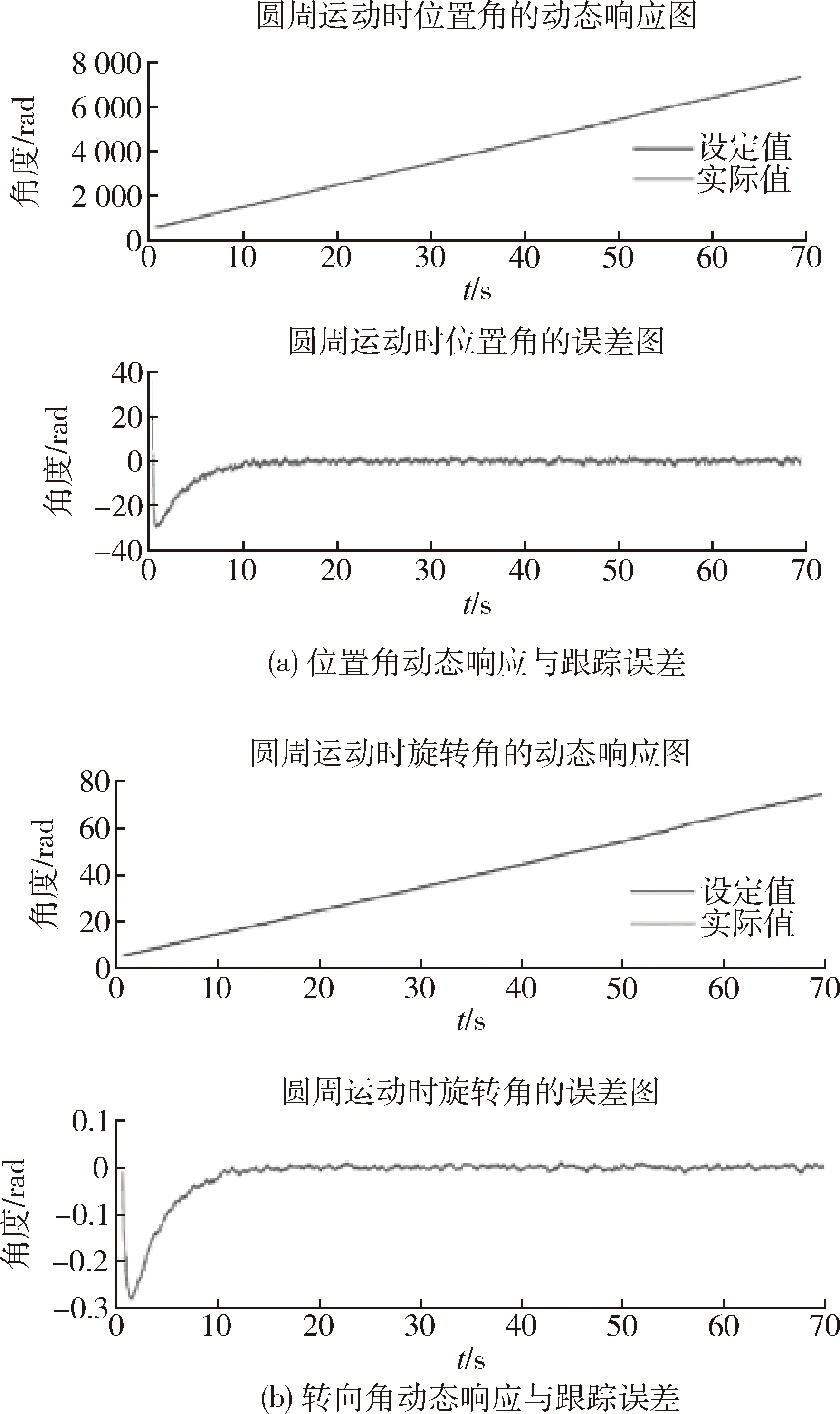
4 结 论
