全状态约束切换系统的自适应神经网络控制
2023-04-19杨山山黄山山邓启志
万 敏, 杨山山, 黄山山, 邓启志
1. 西南石油大学, 成都 610000 2. 中国石油天然气股份有限公司西南油气田分公司, 绵阳 621700
0 引 言
切换系统是一类混杂系统,它是由有限个数子系统和控制子系统切换次序的切换律(切换信号)构成的[1].实际上,许多系统都可以通过切换特性进行描述,例如汽车变速系统[2]、电压转换系统[3]、智能机器人系统[4]、网络控制系统[5]和飞行器控制系统[6]等.因此,切换系统也受到了国内外学者的广泛关注,并且也得到了一些理论成果[7-9].目前,对于非线性切换系统的稳定性分析主要有两种方法:共同Lyapunov函数法和多Lyapunov函数法以及其衍生的平均驻留时间,这两种设计方法能有效地解决非线性切换系统的稳定和跟踪控制问题.文献[10]针对一类切换不确定非线性系统,基于平均驻留时间和反步法设计了一种新的自适应模糊控制技术.文献[11]针对一类切换不确定非线性系统,设计了一种基于共同Lyapunov函数的自适应模糊反馈控制方法.但是以上文献中使用的反步法由于在推导过程中需要每一步都对虚拟控制求导,使得神经网络控制器的输入变量急剧增多,设计的控制器随着系统阶数的增高而变得愈发复杂,即存在着“复杂性爆炸”问题,因此上述文献中的成果还存在着一些不足.
状态约束是指系统由于安全性和性能因素等原因要求其某些状态在暂态和稳态时满足一定的约束条件.在实际工业生产中,如果忽视这些约束限制带来的系统状态“越界”的情况,可能就会引发严重的事故,造成不必要的财产损失,因此对于状态约束控制的研究是非常必要的.目前对于状态约束控制的研究多是引入合适的BLF防止系统违反相应的约束条件.文献[12]针对一类主动悬架系统的状态约束问题,提出了一种基于反步法和BLF的自适应输出反馈控制方法.但是该文献研究的系统约束条件是静态约束,缺乏一般性.文献[13]针对未建模动态的非线性切换系统,研究了基于状态约束的自适应神经网络的跟踪控制问题.但是该文献控制器的设计需要系统的所有状态都是可测的,然而大多数情况下仅仅只有系统的输出信号是可以直接测量的.文献[14]针对一类具有全状态约束和状态不完全可测的严格反馈非线性系统,提出了一种基于RBF神经网络状态观测器的动态表面输出反馈控制技术,达到了良好的控制精度.但是其没有考虑存在切换系统的情况,也没有解决切换系统的稳定性问题.
本文的特点在于,工程实际系统通常是一个受多种因素影响的复杂系统,而针对具有全状态约束、状态不完全可测以及未知外部干扰的非线性系统进行研究而设计的控制算法是更符合工程实际的.不过,由于反步设计方法中“复杂性爆炸”问题的局限性,设计的控制器也大多只能应用于一些低阶实际系统.因此利用动态表面控制技术,即在反步设计方法中引入一阶滤波器,将复杂的微分运算变为简单的代数运算,从而避免了控制器设计过程中反复对虚拟控制律求导的过程,极大地简化了控制器的设计过程;通过对带电机驱动的机械臂模型进行仿真实验,结果也表明设计的控制算法能有效应用于实际工程模型,指导工程实践.
1 被控系统模型及准备
1.1 系统模型描述及基本假设
考虑如下一类严格反馈非线性切换系统,其形式如下所示:
(1)
其中:X=[x1x2…xn]T∈Rn,i=1,2,…,n-1是状态向量,且只有x1是可测的;uσ(t)∈R是控制信号,σ(t):[0,∞)→M={1,2,…,m}是系统的切换信号,并且它是一个右分段连续函数;当σ(t)=k时,即第k个子系统处于运行状态,uk∈R是第k个子系统的控制器输入,y∈R是系统的输出,fi,σ(t)(i=1,2,…,n)是一个未知非线性光滑函数,di,σ(t)(t)(i=1,2,…,n)是未知扰动.
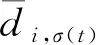
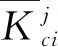
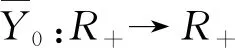
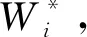
(2)


控制目标:1)设计一个自适应输出反馈控制器,使得输出y(t)能够跟踪期望轨迹yd(t),且跟踪误差z1=y-yd尽可能小;2)保证闭环系统中所有信号有界;3)系统中的所有状态都不违反约束.
1.2 神经网络状态观测器设计
对于第k个子系统,非线性切换系统(1)可以写成如下形式:
(3)

(4)
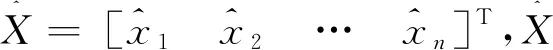
(5)
其中,

(6)

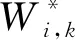
(7)

因此,最小逼近误差可以表示成如下形式:
(8)

将式(5)和式(8)代入式(3)可得
(9)
因此对于第k个子系统,神经网络状态观测器可以设计成如下形式:
(10)

(11)

2 自适应控制律设计
对于自适应控制律的推导过程包括n步,通过在每一个步骤中选择恰当的障碍Lyapunov函数Vi,k,i=1,2,…,n,k∈{1,2,…,m}来构造虚拟控制律.控制器设计步骤如下:
定义z1为跟踪误差,zi为虚拟误差,αi-1,k为虚拟控制律,同时引入一阶滤波器,有
(12)
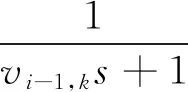
步骤1:对z1进行求导,可得
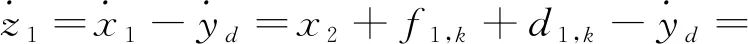
(13)
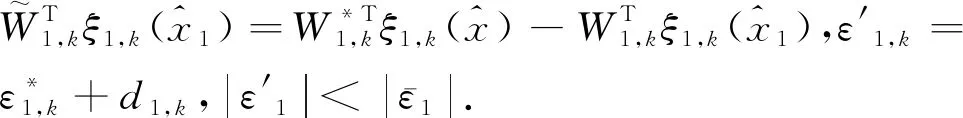
定义如下函数:
(14)
(15)
(16)
选择如下的非对称时变BLF:

(17)
其中,γ1,k>0是设计参数.
通过对误差进行坐标变换,有

(18)
将式(18)代入式(17),有
(19)

(20)
由于,
(21)
(22)
(23)
因此,有

(24)
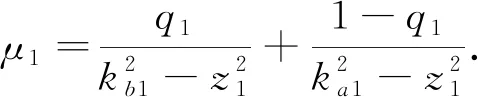
根据Young’s不等式,有
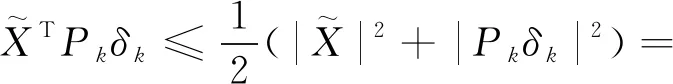
(25)
(26)
(27)
由式(25)、式(26)和式(27),可得
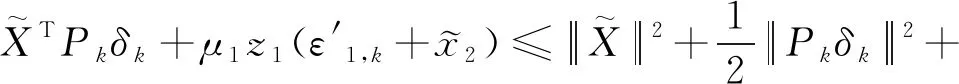
(28)
将式(28)代入式(20)得

(29)
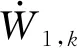
(30)
(31)
其中,c1,k>0和φ1,k>0是设计参数,
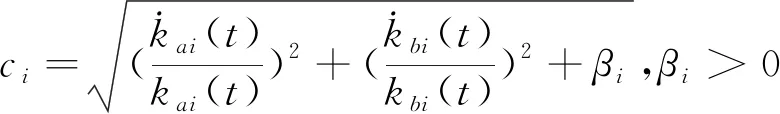
根据Young’s不等式,有

(32)
(33)
将式(21)、式(22)和式(23)代入式(20),有

(34)
步骤 i(2≤i≤n-1):对zi进行求导,可得

(35)
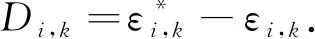
定义如下函数:
(36)
(37)
(38)
其中,ψi-1,k是αi-1,k的最大绝对值.
选择如下的非对称时变BLF:

(39)
其中,γi,k>0是设计参数.
对误差进行坐标变换,有
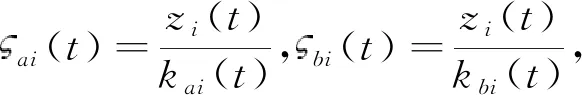
(40)
将式(40)代入式(39),有
(41)
则Vi,k的时间导数为

(42)
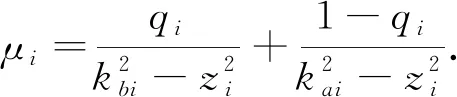
利用Young’s不等式,有
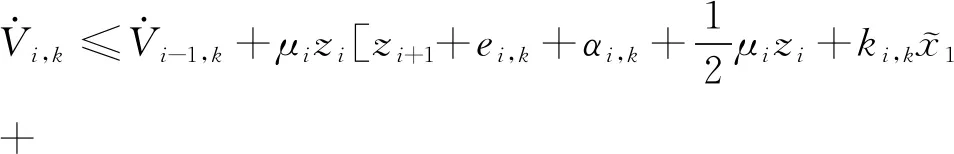
(43)
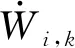

(44)
(45)
其中,ci,k>0和φi,k>0是设计参数.
由式(44)和式(45),有
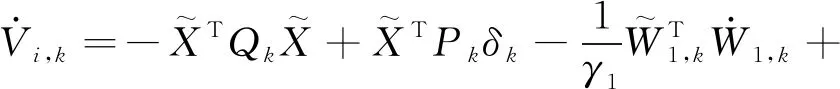
(46)
步骤 n:在最后一步中,系统的控制输出为u,有

(47)
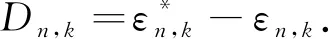
定义如下函数:
(48)
(49)
(50)
选择如下的非对称时变BLF:

(51)
其中,γn,k>0是设计参数.
对误差进行坐标变换,得
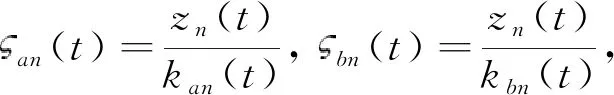
(52)
因此,有
(53)
由于
(54)
(55)
(56)
Vn,k的时间导数为

(57)
利用Young’s不等式,有
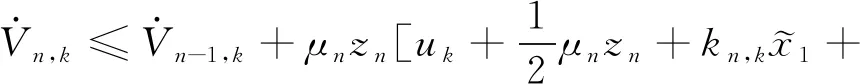
(58)
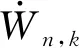
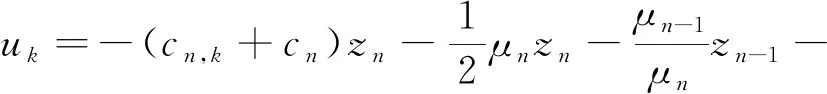
(59)
(60)
其中,cn,k>0和φn,k>0是设计参数.
由式(59)和式(60),有
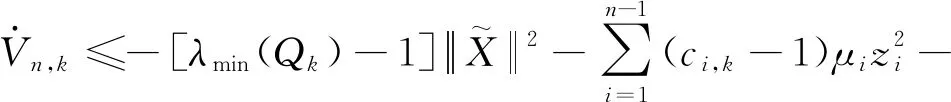
(61)
3 全状态约束切换系统稳定性分析
定义闭环系统的Lyapunov函数为Vk=Vn,k,因此可以得到Vk的导数,有
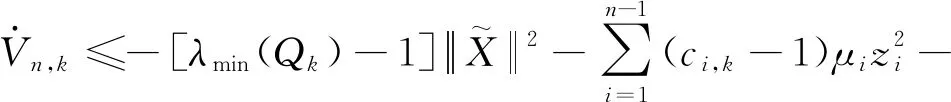
(62)
根据文献[11],有
(63)
其中,B1,k(.)是连续函数.
因此,有
(64)

当Vk=p时,连续函数Bi,k(·)有界,且存在一个最大值Mi,k[11].
根据Young’s不等式,有
(65)
(66)
根据引理2,可得
(67)
所以由式(37),有

(68)
其中,
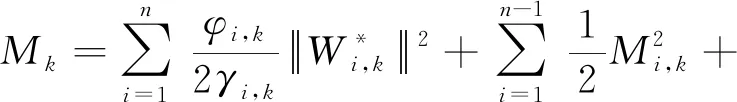
通过选择合适的Qk、ci、cn和νi,有
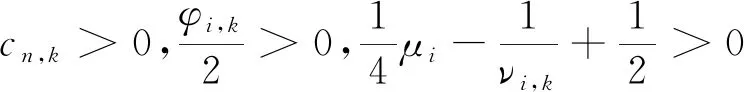
(69)
其中,i=1,2,…,n-1.
定义正参数
(70)
定义C=minCk和D=maxMk,因此,式(43)可以写成如下形式:
(71)
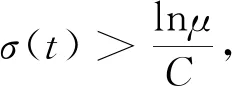
证明:W(t)=eCtVσ(t)(x(t))是系统方程式(1)的解且分段可微.根据式(46),在每一个[tj,tj+1)区间里,有
(72)
同式(15)的证明方式,有
(73)
其中,μ>1,且k,l∈M.因此,可以得到
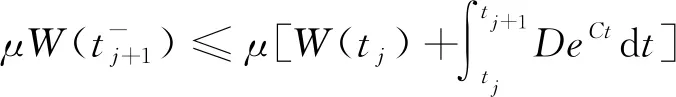
(74)
对于任意T>t0=0,将不等式(74)从j=0迭代到j=Nσ(T,0)-1,有
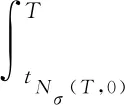
(75)
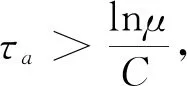
因此,可得
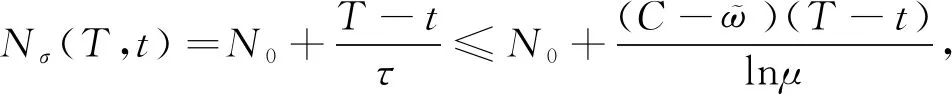
(76)
Nσ(T,0)-j≤1+Nσ(T,tj+1)(j=0,1,…,Nσ(T,0)),因此,有如下关系式:
μNσ(T,0)-j≤μ1+N0e(C-ϖ)(T-tj+1)
(77)
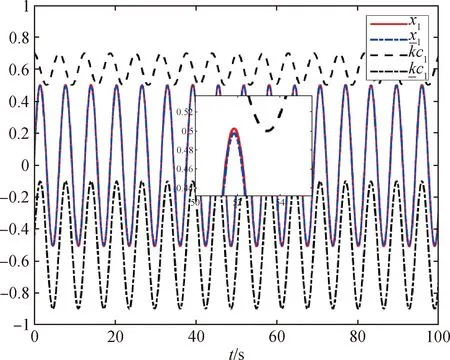
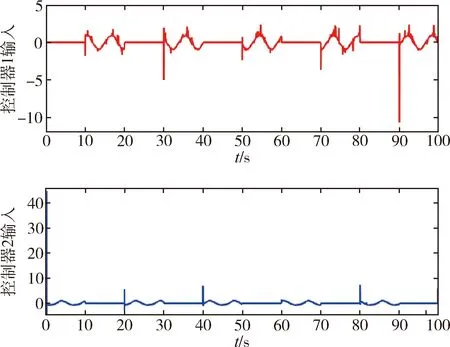
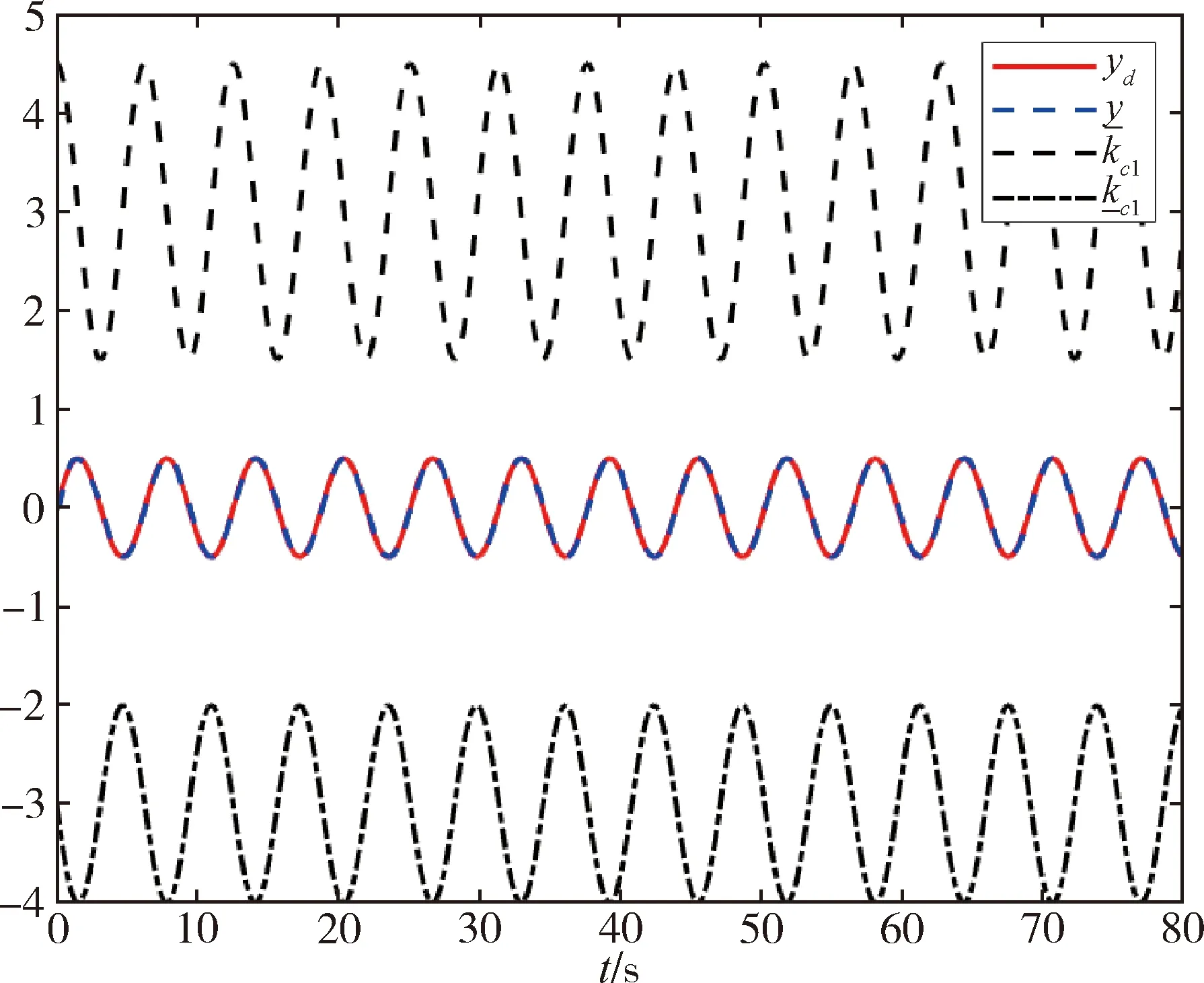
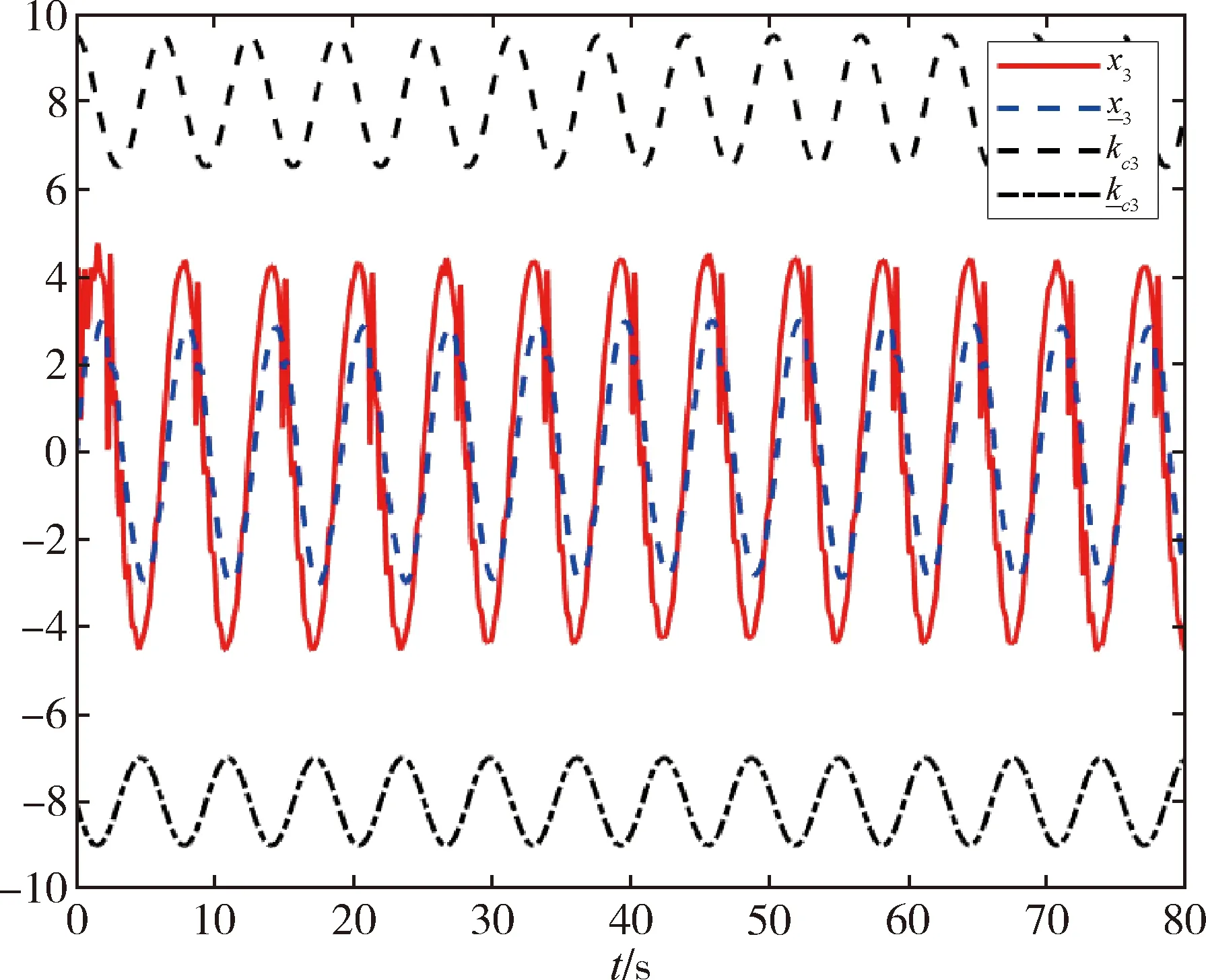
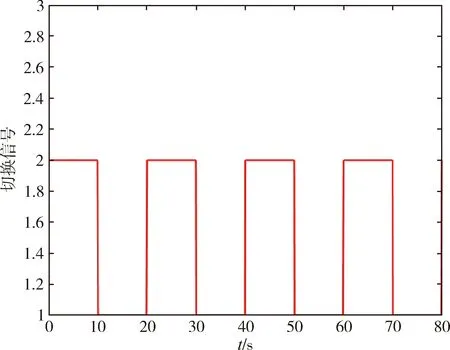
因为ϖ (78) 将式(77)和式(78)代入式(75),可得 (79) 因此,有 (80) 由式(55),可得 (81) (82) 因此,可得 (83) 式(83)表明,状态观测器的误差可以通过选择适当的设计参数减小[20]. 上述控制系统的主要结构如下图1所示. 图1 全状态约束切换系统控制策略图Fig.1 Control policy diagram of the full state constrainedswitched system 例1 本节将对具体的算例进行仿真,对所提出的控制效果进行仿真验证.考虑如下严格反馈非线性切换系统: 设计如下的带有观测器的自适应切换控制器: 其中,n=1,2,k=1,2. 采用高斯基函数作为RBF神经网络基函数来进行相关算法的设计,其结构如下所示: 其中,i=1,2,…,n,k=1,2,…,n. 图2 系统输出y和参考信号yd的跟踪轨迹Fig.2 Tracking trajectories of system output yand reference signals yd 图3 跟踪误差z1Fig.3 The tracking error z1 图4 系统状态x1和其状态观测值的轨迹Fig.4 The trajectory of system state x1and its state 图5 系统状态x2和其状态观测值的轨迹Fig.5 The trajectory of system state x2and its state 图6 切换信号Fig.6 Switched signal 图7 控制器轨迹Fig.7 Controller trajectory 例2 例1通过数值仿真实验探究了本文设计的一种切换自适应控制算法在理论层面的可行性.基于上述基础,本例将探讨该控制算法在工程实际系统层面上应用的可行性. 针对一个带电机驱动的单关节机械臂系统进行轨迹跟踪控制,其动态方程为[21]. 考虑上述单关节机械臂系统中存在着如下的切换函数,则其可以表示为 其中,f1,1(x1,x2,x3)=f1,2(x1,x2,x3)=0,f2,1(x1,x2,x3)=-(B/D)x2-(N/D)sinx1+sinx1x2,f2,2(x1,x2,x3)=-(B/D)x2-(N/D)sinx1,f3,1(x1,x2,x3)=-(Km/M)x2-(H/M)x3+sinx1,f3,2(x1,x2,x3)=-(Km/M)x2-(H/M)x3,d1,2(t)=d1,1(t)=d3,1(t)=d3,2(t)=0,d2,1(t)=d2,2(t)=0.1sin(0.1t).参考信号为yd=0.5sint. 控制器的设计如下: 控制器的设计参数为γi,k=1(i=1,2,3,k=1,2);φi,1=5,φi,2=3(i=1,2,3);k1,1=k1,2=22,k2,1=150,k2,2=148,k3,1=200,k3,2=202;c1,1=32,c1,2=30,c2,1=c2,2=6,c3,1=1.1,c3,2=1.RBF神经网络的参数设置如下:网络节点为l1=l2=l3=6,高斯函数中心分布在[-5,5],因此有mi=[-5 -3 -1 1 3 5],i=1,2,3. 图8 位置输出信号y和参考信号yd的跟踪轨迹Fig.8 The tracking trajectory of position output signal yand reference signal yd 图9 跟踪误差z1Fig.9 The tracking error z1 图10 位置输出信号x1和其状态观测值的轨迹Fig.10 The trajectory of position output signal x1and its 图11 速度信号x2和其状态观测值的轨迹Fig.11 The trajectory of velocity signal x2and its 图12 电机转矩x3和其状态观测值的轨迹Fig.12 The trajectory of motor torque x3and its 图13 切换信号Fig.13 Switched signal 图14 控制器轨迹Fig.14 Controller trajectory 设计的自适应动态面输出反馈控制器,能够很好的控制一类具有全状态时变约束、状态不完全可测以及未知外部干扰的不确定严格反馈非线性切换系统.通过Lyapunov方法、平均驻留时间理论和数值仿真实验分别从理论和实验层面验证了设计的控制算法的有效性.最后,带电机驱动的单关节机械臂仿真实验也表明该控制方法能够有效应用于实际工程模型.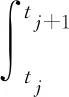



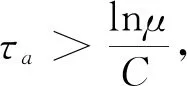

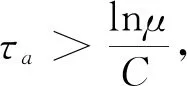

4 仿 真


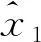










5 结 论
